George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

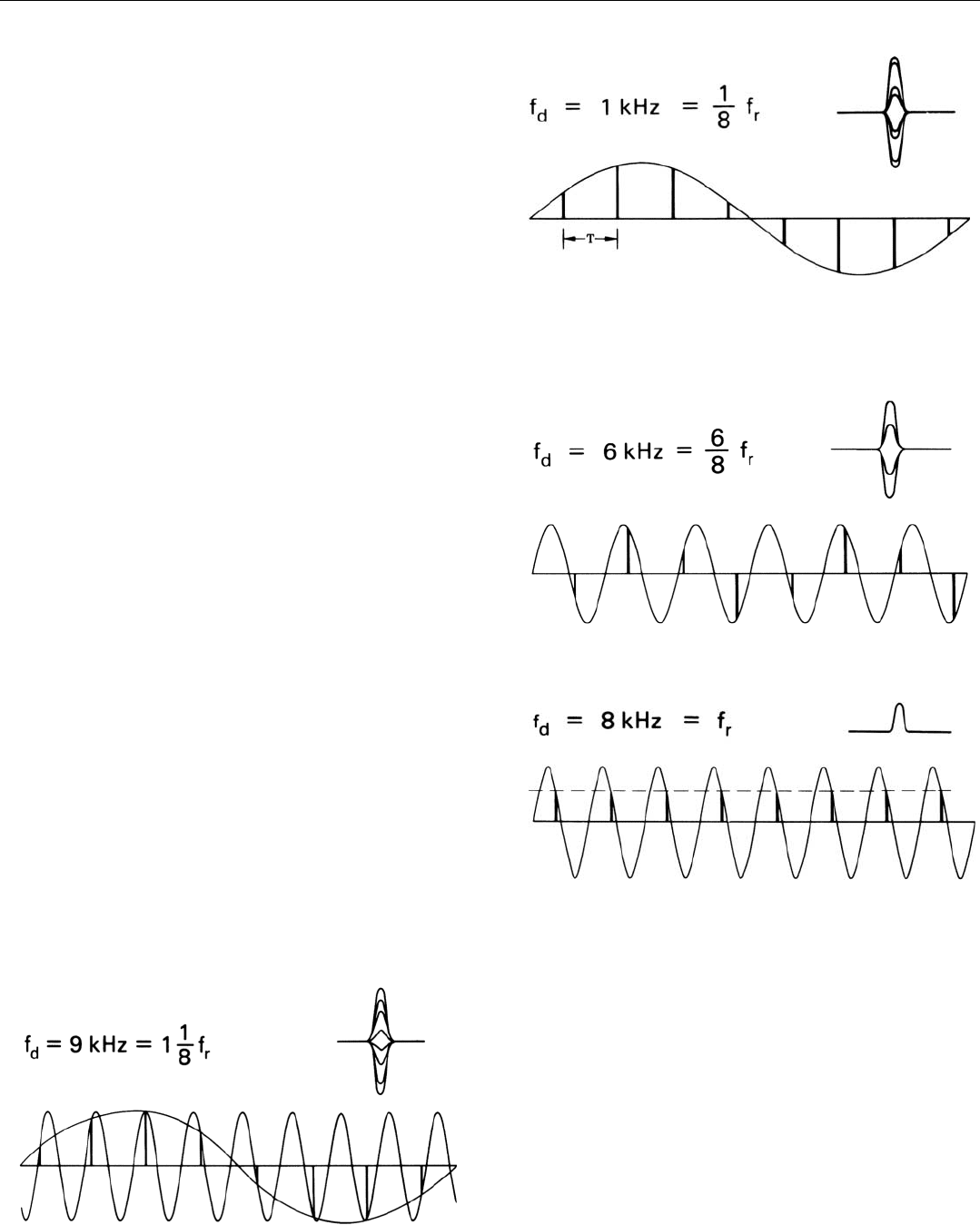
From the standpoint of filtering, though, the important

characteristic of the I and Q samples when the doppler shift

is zero is that their individual amplitudes do not fluctuate.

Moving on to the target whose doppler frequency is 1

kilohertz (Fig. 4), the amplitude of its pips fluctuates wide-

ly from pulse to pulse. The reason for this, too, can be

readily seen. Because the echoes do not have the same radio

frequency as the reference signal, their phase relative to it

changes from pulse to pulse. The amount of change is 360°

times the ratio of the target’s doppler frequency to the PRF.

In this case (doppler frequency, 1 kilohertz; PRF, 8 kilo-

hertz) the ratio is 1/8. The doppler frequency “wave” is, in

effect, being sampled at intervals of 360° x

/8 = 45°.

(Again, the magnitude of the vector sum of the I and Q

samples equals A, but the phase of the sum cycles through

360° at a rate equal to the doppler frequency.)

For the target whose doppler frequency is 6 kilohertz

(Fig. 5), the story is the same. The only difference is that, in

this case, the samples are taken at intervals of 360° x

/8 =

270°.

As a result, not only does the amplitude of the detector’s

output fluctuate widely, but as the target return slides into

and out of phase with the reference frequency, the samples

alternate between positive and negative signs.

For the target whose doppler frequency is 8 kilohertz,

though, the pips once again have a constant amplitude

(Fig. 6). The reason, of course, is that the doppler frequen-

cy and the PRF are equal. The samples are all taken at the

same point in the doppler frequency cycle. There is, in fact,

no way of telling whether the doppler frequency is zero, or

, or some integer multiple of f

Similarly, if echoes are received from a target having a

doppler frequency of 9 kilohertz (Fig. 7, below), the pips it

produces will fluctuate at exactly the same rate as the pips

produced by the target having a doppler frequency of 1

kilohertz. The observed frequency is ambiguous.

CHAPTER 19 How Digital Filters Work

255

4. Detector output varies sinusoidally from pulse to pulse.

5. Detector output alternates between positive and negative values.

6. Detector output is similar to that for target with zero doppler

frequency.

7. Detector output fluctuates at exactly the same rate as for a target

whose doppler frequency is 1 kilohertz (9 kHz – 8 kHz).

PART IV Pulse Doppler Radar

256

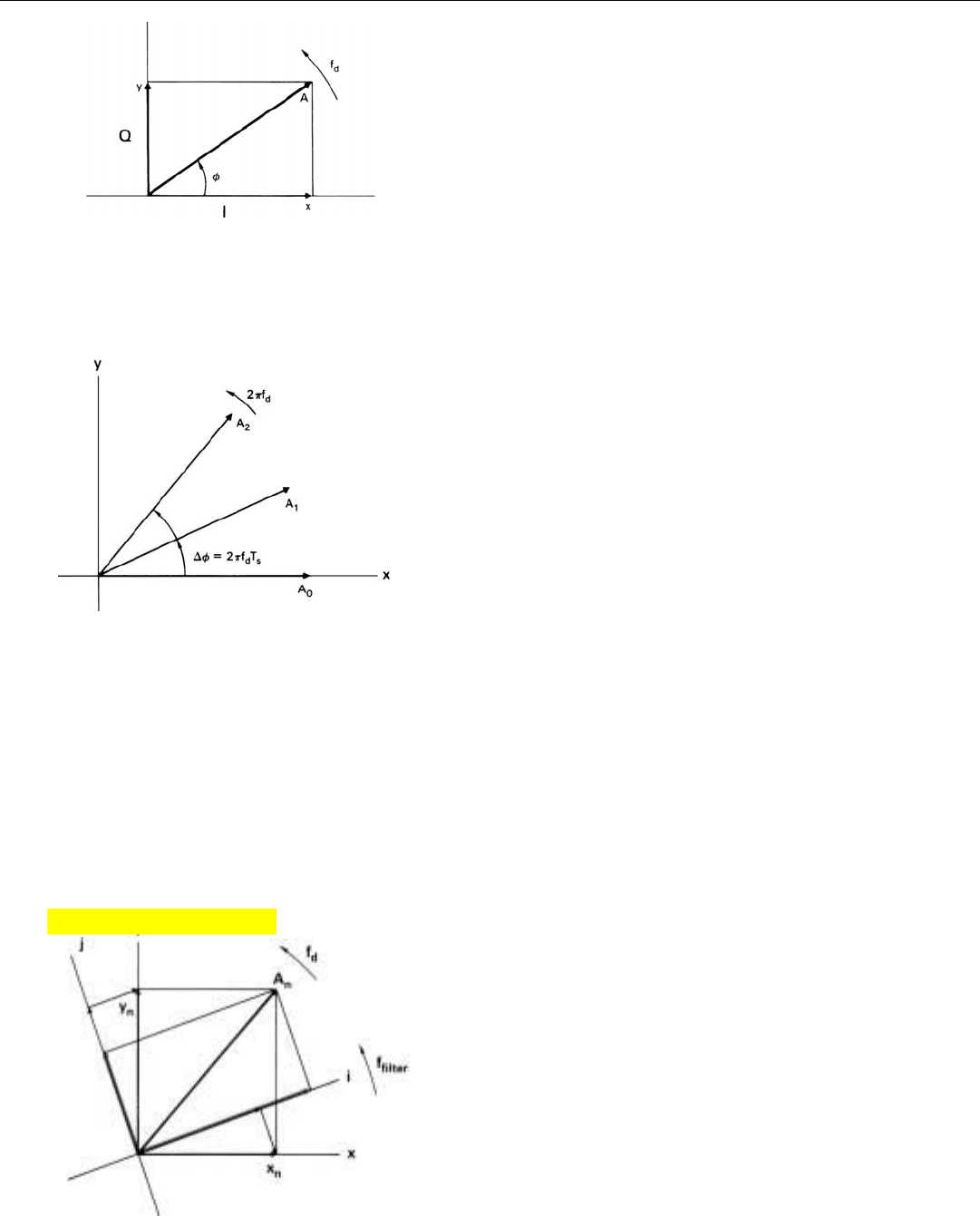
Phasor Representation of the Samples. Everything we

have seen by viewing the detector output at a point on a

range trace corresponding to a particular target’s range can

be presented much more conveniently in a phasor diagram,

such as that shown in Fig. 8. Moreover, a phasor diagram

presents the outputs of both the I and Q detectors simulta-

neously. The length of the phasor corresponds to the ampli-

tude (A) of the target’s echoes. The angle (φ) which the pha-

sor makes with the x axis, corresponds to the radio-fre-

quency phase of the echoes relative to the reference signal.

The length, x, of the projection of the phasor on the x axis

corresponds to the output of the in-phase (I) detector; the

length, y, of the projection on the y axis corresponds to the

output of the quadrature (Q) detector.

The phasor rotates at the target’s apparent doppler fre-

quency, i.e., its true doppler frequency or true doppler fre-

quency plus or minus an integer multiple of the sampling

rate. If this frequency is positive (greater than the reference

frequency), rotation is counterclockwise (Fig. 9); if nega-

tive, rotation is clockwise. The amount that the phasor

steps ahead from sample to sample (∆φ) is 2π radians

(360°) times the doppler frequency times the length of the

sampling interval:

∆φ = 2π f

where f

is the apparent doppler frequency and T

is the

sampling interval. If the sampling rate is the PRF (as it gen-

erally is in all-digital signal processors),

is the interpulse

period, T.

What the Filter Does

Digital filtering is simply a clever way of adding up (inte-

grating) successive samples of a continuous wave so that

they produce an appreciable sum only if the wave’s frequen-

cy lies within a given narrow band—i.e., produce a sum

equivalent to the output which would be produced if the

continuous wave were applied to a narrow band analog fil-

ter. If the variation in amplitude from sample to sample cor-

responds closely to the resonant frequency of the equivalent

analog filter, the sum builds up; otherwise, it does not.

What the filter does, in effect, is project the x and y com-

ponents of the phasor representation of the samples onto a

rotating coordinate system (i and j in Fig. 10). The rate at

which the coordinates rotate—number of revolutions per

second—is made equal to the center frequency of the band

the filter is intended to pass. This rate, f

, can be thought of

as the filter’s resonant frequency: the frequency to which it

is “tuned.”

8. If the sine wave is represented by a phasor (A), the I compo-

nent is the projection of the phasor on the x axis and the Q

component is the projection of the phasor on the y axis.

9. The amount that the phasor steps ahead from sample to sam-

ple (∆φ) is proportional to the target’s doppler frequency.

10. The filter projects the x and y components of the phasor, A

onto a coordinate system (i, j) that rotates at the frequency to

which the filter is “tuned.”

2. In certain applications digital

doppler filtering may be pre-

ceded by some analog filter-

ing (for clutter reduction),

which converts the return to a

CW signal. The sampling rate

then is generally not the PRF.

Click for high-quality image

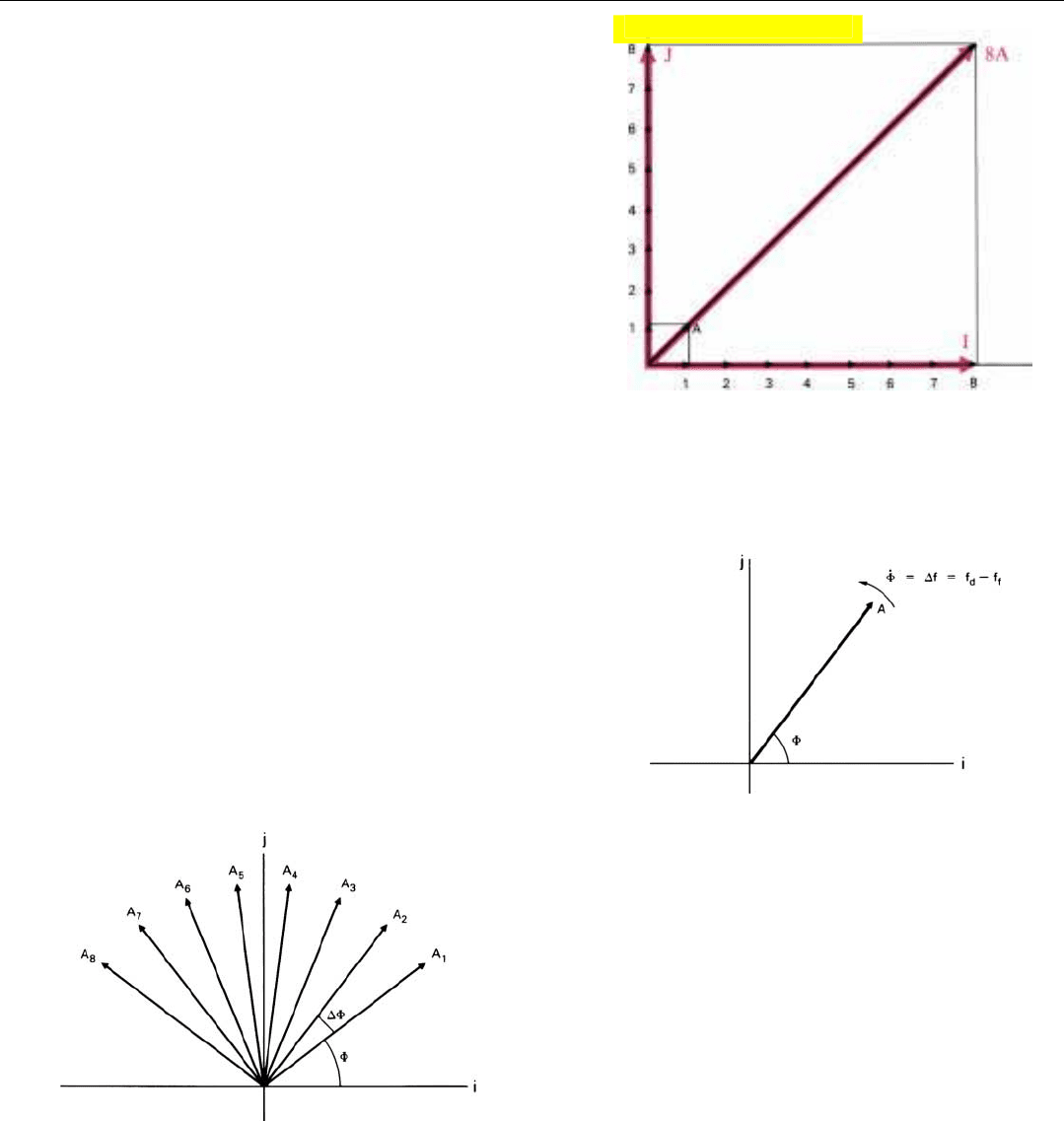
If the frequency of the sampled wave is the same as that

of the filter, the angle between the phasor (A) and the rotat-

ing coordinate system will be the same for every sample

(Fig. 11).

Consequently, after N samples have been received, the

sum of the projections of the x and y components of A on

the i axis will be N times as great as after a single sample

has been received. The same will be true of the sum of the

projections on the j axis.

On the other hand, if the frequencies of the sampled

wave and the filter differ sufficiently, the angle between the

phasor and the rotating coordinate system (i, j) will vary

cyclically and the projections will tend to cancel.

At the end of the integration time, the sum of the projec-

tions on the i axis (I) is added vectorially to the sum of the

projections on the j axis (J). The magnitude of the overall

vector sum is the output of the filter. The quantities I and J

are then dumped and the integration is repeated for the

next N samples.

We can visualize the process most easily if we imagine

that we are riding on the rotating coordinate system (Fig.

12). We then see only the rotation of the phasor relative to

the i and j axes—that is, the rotation (Φ

⋅

) due to the differ-

ence (∆f) between the frequency of the sampled wave and

the frequency of the filter. As we just saw, if ∆f is zero, the

phasor will be in the same relative position each time a

sample is taken. But if the frequencies are different, the

phasor will be in progressively different positions (Fig. 13).

CHAPTER 19 How Digital Filters Work

257

11. If the target’s doppler frequency and the filter frequency are

the same, after eight pulses have been integrated, the magni-

tude of the vector sum of the phasor’s projections on i and j

will be eight times the phasor’s amplitude.

12. If we were to ride on the rotating coordinate system (i, j), we

would see only the rotation, Φ

⋅

, of the phasor (A) due to the differ-

ence between the frequencies of the sampled wave and the filter.

13. If the frequencies of the sampled wave and the filter differ,

the phases of successive samples will differ by ∆Φ.

The phase difference, ∆Φ, between successive positions is

directly proportional to the frequency difference. In radians

∆Φ = (2π T

) ∆f

where 2π is the number of radians in one revolution, T

the sampling interval, and ∆f is the difference between the

frequencies of the sampled wave and the filter.

Click for high-quality image

PART IV Pulse Doppler Radar

258

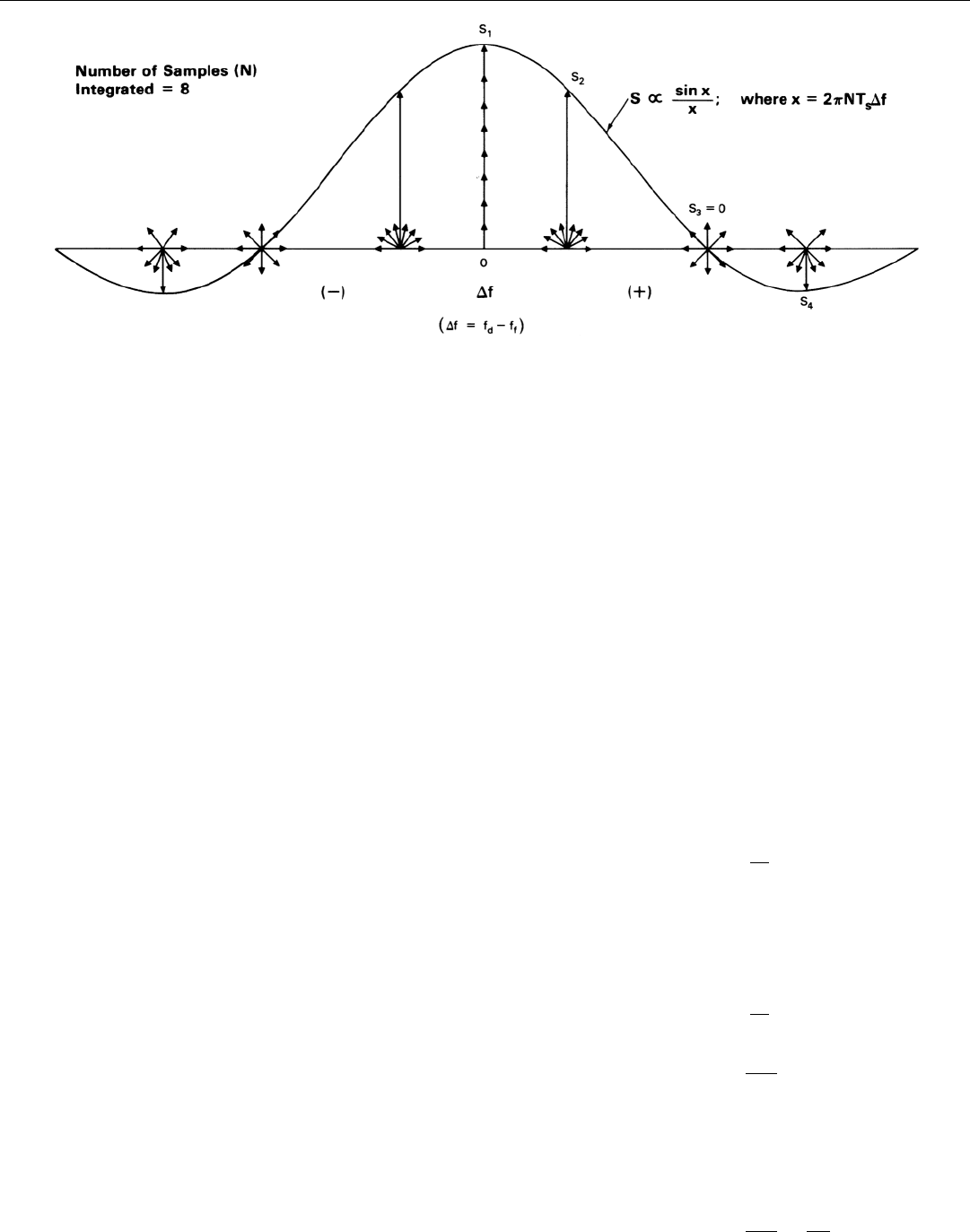
As you can see from the phasor diagrams in Fig. 14, if

the frequency difference ∆f (hence also ∆Φ) is gradually

increased, the phasor positions fan out increasingly, and the

extent to which the samples cancel correspondingly

increases.

A point is soon reached where the phasor positions are

fanned out over a full 360°. The sum of the samples is then

zero; a null in the filter characteristic has been reached.

Beyond this null, the filter output goes through a succes-

sion of sidelobes.

For a given amplitude of the sampled signal, a plot of the

amplitude of the filter output versus ∆f has a sin x/x shape.

The band of frequencies between the first pair of nulls is

the filter’s passband.

Since 360° is 2π radians, after N samples have been inte-

grated, the value of ∆Φ for which the first nulls occur is 2π

divided by N.

∆Φ

2π

By substituting the expression we derived earlier for ∆Φ

(2πT

∆f), we can find the difference, ∆f, between the fre-

quencies of the wave and the filter at the nulls.

2πT

∆f=

2π

∆f =

The number of samples integrated (N) times the sam-

pling interval (T

) is of course the filter integration time

int

). Therefore, the null-to-null bandwidth is

int

14. If difference (∆f) between frequencies of sampled signal and filter is increased, phasors representing successive samples will fan out increas-

ingly and the magnitude of their sum (S) will vary as sin x/x.

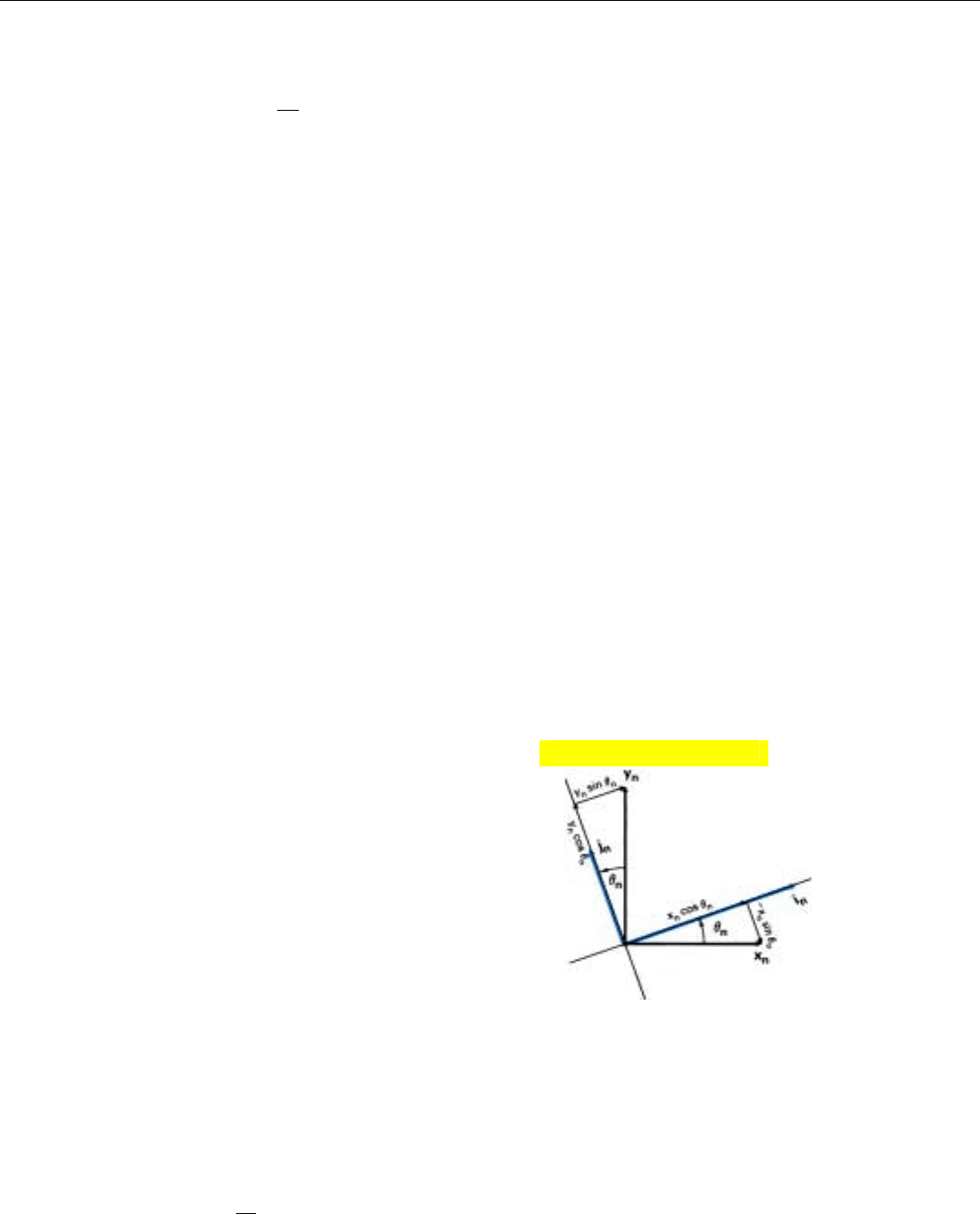
The 3-dB bandwidth of a sin x/x curve is roughly half the

null-to-null bandwidth, so

3 dB

≅

int

Thus, the more samples integrated and the longer the sam-

pling interval—i.e., the greater t

int

—the narrower the pass-

band will be. Interestingly, if integration is performed serial-

ly, the passband is in a sense dynamic; throughout the inte-

gration period it narrows, reaching its final width only at

the end of the period.

As noted previously, if the samples received as inputs by

the filter are due to the return from a target, the amplitude

(A) of the phasor representation of the sampled signal will

be proportional to the power of the target echoes. The filter

output then will be proportional to the power of the echoes

times the integration time and so will be proportional to the

total energy received from the target during t

int

. The con-

stant of proportionality will have its maximum value if the

target’s doppler frequency is centered in the filter passband.

The constant will be zero if the doppler frequency is the

same as one of the null frequencies. Otherwise, the con-

stant will have some intermediate value determined by the

filter’s sin x/x output characteristic.

Discrete Fourier Transform

The algorithms which must be repeatedly computed to

project the in-phase and quadrature components of succes-

sive samples of a wave (x

and y

) onto the rotating coordi-

nates (i and j) can be derived on sight from the geometry of

Fig. 15. They are

= x

cos

+ y

sin

= y

cos

– x

sin

where i

and j

are the projections of x

and y

on the

rotating coordinates and

is the angle between the coordi-

nate systems.

The terms cos

and sin

are called the filter coeffi-

cients. The amount that

changes from one sampling inter-

val to the next—∆

—is 2π times the product of the filter

frequency and the sampling interval, T

. If the sampling

rate is the PRF, then T

= 1/f

, and

∆

360°

where f

is the filter’s frequency and f

is the PRF.

CHAPTER 19 How Digital Filters Work

259

15. The algorithms which must be repeatedly computed to per-

form the integration may be derived on sight from the rela-

tionships illustrated here.

= x

cos

+ y

sin

= y

cos

– x

sin

Click for high-quality image

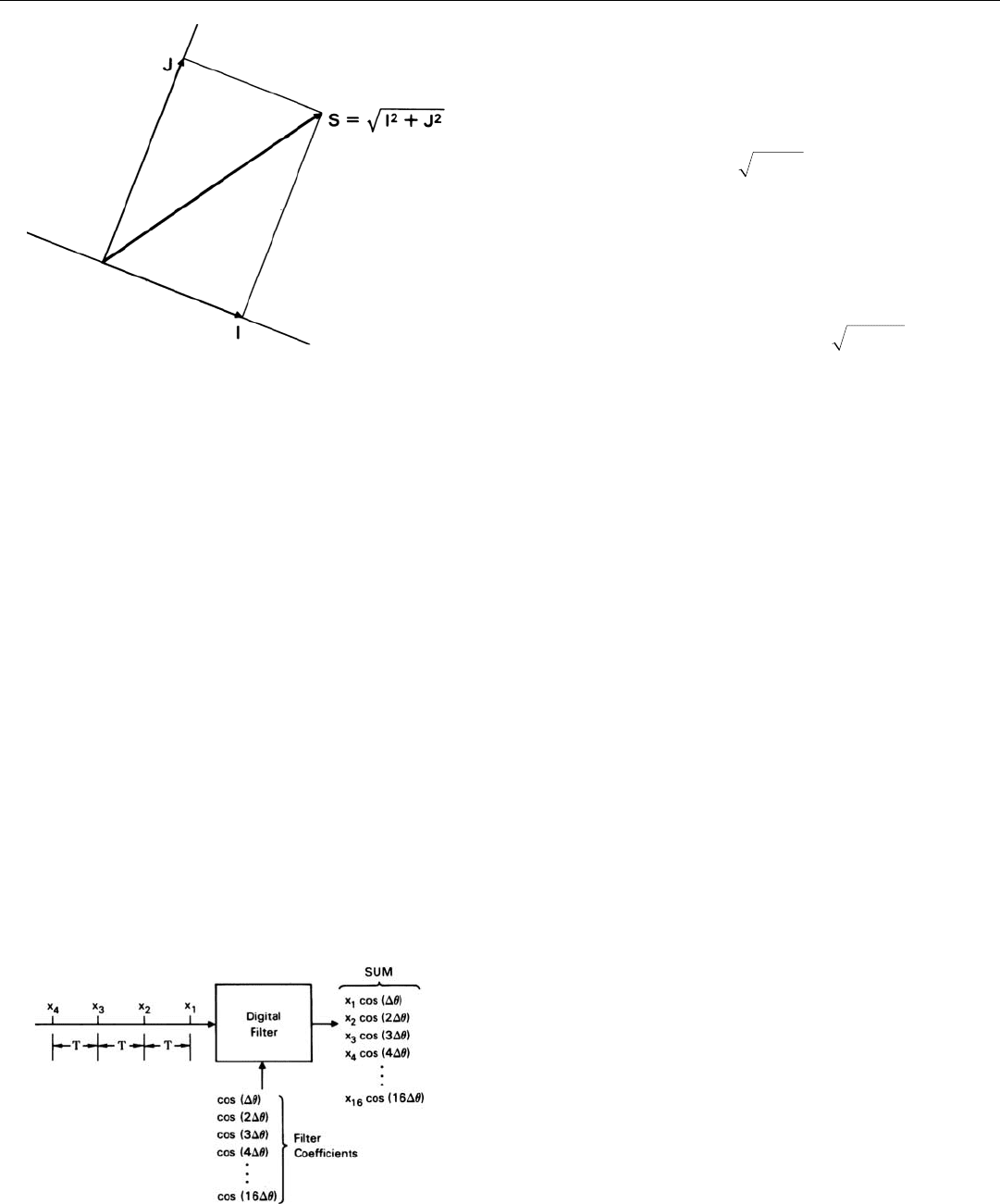
As the values of I and J are computed, they are separately

summed. At the end of the integration period, the sums are

added vectorially (Fig. 16). For this, the equation which

must be solved is

S = I

+ J

where I and J are the sums of the values of i and j, respec-

tively, for the samples taken during the integration period.

The output of the filter is the quantity, S. (Often, to avoid

taking the square root, which is comparatively time con-

suming, an algorithm approximating I

+ J

is used to

compute S.)

Taken together, the iterations of the algorithms for I and

J for a single integration period plus the algorithm for S

constitute the discrete Fourier transform, DFT. “Discrete”

connotes that the transform applies to discrete-time samples

of a time-varying function—the sampled wave—rather than

to the continuous function of time, itself.

Implementing the DFT

The sequence of operations which a computer must

carry out to implement the discrete Fourier transform may

be most easily seen if we consider first a simple filter pro-

cessing one component (say the in-phase component, x) of

the return from a single range increment. We can then

move on to the processing of return from a contiguous

series of range increments and, finally, to the processing of

both in-phase and quadrature components.

Single-Channel Filter. To project the component x

, of

successive pulses onto a single rotating coordinate, i, only

one term of the DFT must be repeatedly computed.

= x

cos

Other than summing successive values of i, no other com-

putation is required.

For any one range increment (Fig. 17), the input to the

computer consists of a succession of digital numbers—x

, x

, etc. Since all of these numbers represent echoes

reflected from the same range, successive numbers are

received by the computer at the same point in successive

interpulse periods. Their arrivals are thus separated by T

seconds, T being the interpulse period.

Now, the computer’s job is to multiply each number by

the coefficient, cos

; add up the products for some pre-

specified number of inputs, N; and output the accumulated

PART IV Pulse Doppler Radar

260

16. The algorithm which must be computed to add the sums vecto-

rially at the end of the integration period may be derived on

sight from the relationships illustrated here.

17. Inputs to a single-channel filter for a single-range increment.

The filter’s job is to multiply successive values of the in-phase

component of the target signal (x

, x

, etc.) by prestored co-

efficients and sum the products.

3. The Fourier transform for a

continuous function of time

(pulse-modulated sine wave)

was derived in Chap. 17.

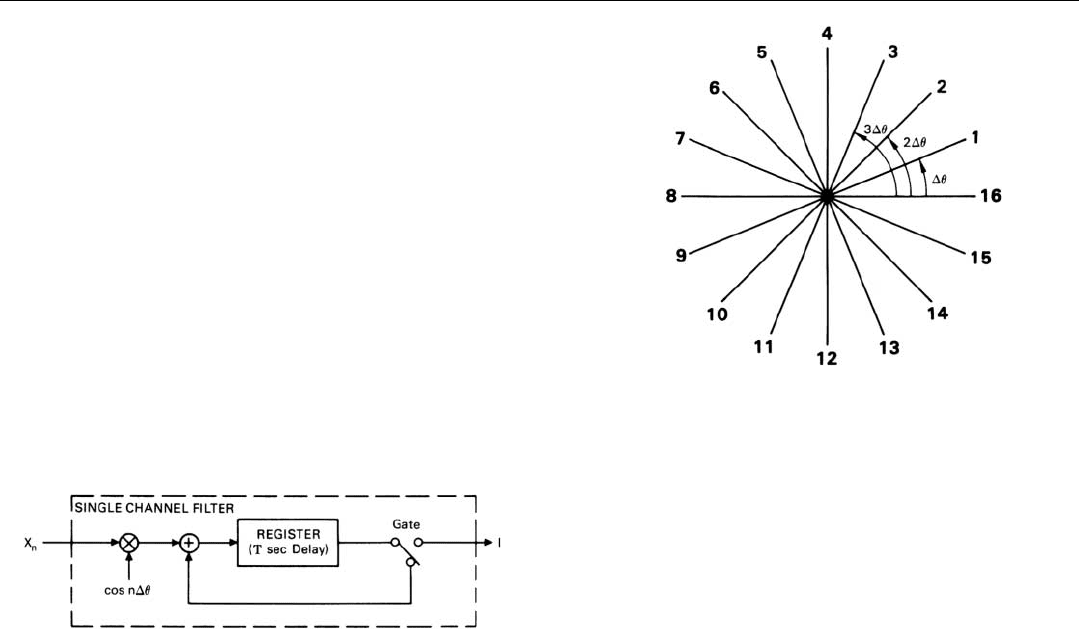
sum. The computer repeats this process over and over

again. For purposes of explanation, we will assume here

that N is 16.

If we represent the pulse-to-pulse change in

for the

particular frequency to which the filter is tuned by ∆

and

for the sake of simplicity assume that the initial value of

∆

, the values of the coefficients for each set of 16 inputs

will be cos ∆

, cos 2∆

, cos 3∆

, cos 4∆

, . . . cos 16∆

(Fig. 18).

When the first input, x

, is received, the computer multi-

plies it by cos ∆

and adds the product into a register,

where it is held for T seconds.

When the second number, x

is received, the computer multiplies it by cos 2∆

, retrieves

the stored product from the register, adds the two products

together, and returns the sum to the register (Fig. 19).

CHAPTER 19 How Digital Filters Work

261

18. Values of

for a filter designed to integrate 16 pulses.

19. Functions performed by a single-channel filter. After N inputs have

been integrated, gate closes and sum (I) is output.

4. “Register” here connotes a

memory position which only

an entire digital number may

be entered into or retrieved

from.

The process is repeated for x

through x

without change.

However, before x

is received, a switch (gate) is temporarily

thrown, allowing the sum which has accumulated in the reg-

ister to pass on to the output. The switch is then returned to

its original position, and the integration process is repeated

for x

through x

. In general, for every value of x, the filter

must perform one multiplication and one addition.

Processing Returns from Successive Ranges. If returns

from more than one range increment are to be processed,

instead of receiving an input of only one number in every

interpulse period, the computer receives a continuous

stream of numbers. During the first interpulse period, it

successively multiplies the number (x

) for each range

increment by cos ∆

, storing the individual products in

separate registers. During the next interpulse period, the

computer multiplies the number (x

) for each range incre-

ment by cos 2∆

, adds this product to the previously stored

product, and so on.

Thus, over the same integration period, the computer

forms a separate filter—tuned to the same frequency—for

the returns from every range increment. If, for example,

returns from 100 range increments are processed, the com-

puter forms 100 filters during every integration time for just

this one doppler frequency.

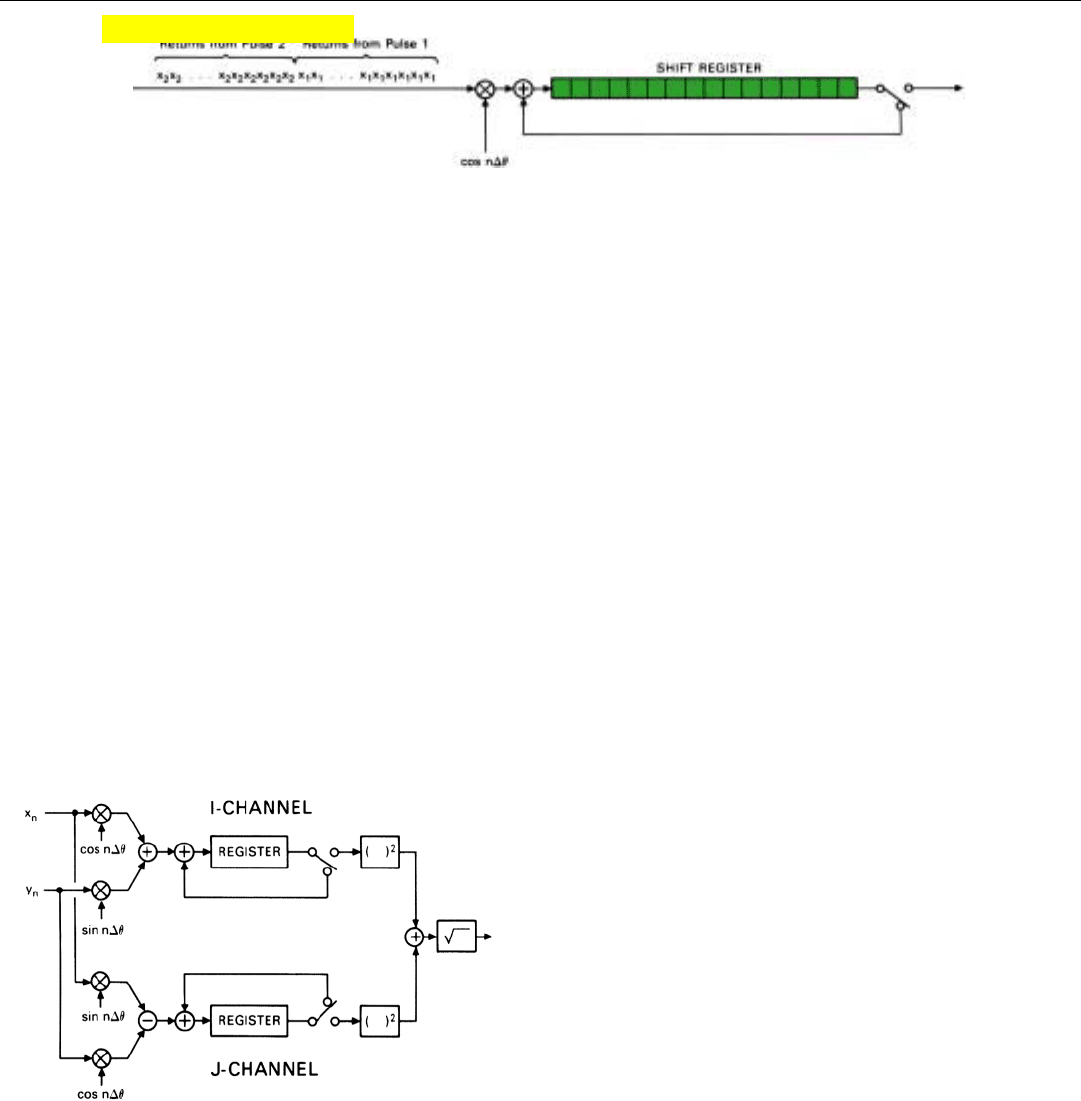
PART IV Pulse Doppler Radar

262

In simple processors, the products may be stored in what

is called a shift register (Fig. 20). It has as many storage

positions as there are range increments. Each time a new

product is produced, the stored sums are all shifted one

position (to the right in the figure). The new product is

added to the sum that has spilled out of the last position,

and the resulting sum is stored in the memory position

which has just been vacated (at the left end of the register).

Since the simple filters we have considered so far process

only one component of the return, they cannot, of course,

discriminate between positive and negative doppler fre-

quencies. If the frequency to which a filter is tuned is 10

kilohertz, for example, the filter will pass return whose fre-

quency is (f

– 10 kHz), just as well as return whose fre-

quency if (f

+ 10 kHz). To differentiate between positive

and negative doppler frequencies, both in-phase and quad-

rature components must be processed. The computing then

is done essentially in two parallel channels.

Two-Channel Processing. A two-channel filter is similar

to a single-channel filter, but is more complex. Two registers

are required—one for the in-phase channel and one for the

quadrature channel (Fig. 21). For each echo from the same

range increment, the filter receives two inputs, x

and y

For the in-phase channel, x

is multiplied by cos n∆

just as in the single-channel filter. However, y

must simul-

taneously be multiplied by sin n∆

. This second product

must then be added to the first. The sum (x

cos n∆

+ y

sin n∆

) is stored in the register.

Similarly, for the quadrature channel, y

is multiplied by

cos n∆

and x

is multiplied by sin n∆

. In this case,

though, the second product is subtracted, and the differ-

ence is stored in the register.

At the end of each integration period, the magnitude of

the integrated target signal is calculated by vectorially

adding the outputs of the two channels. For this, each out-

put is individually squared. The squares are then added

together, and the square root is taken of the sum. This root,

or an approximation of it such as illustrated at the top of

the facing page, is the output of the filter.

20. When returns from successive range increments are processed, the sums for the individual increments may be stored in a shift register. As

each new number is received, sums shift one position to the right.

21. Mechanization of a two-channel filter. Inputs x

and y

are

applied to both channels. At end of every integration period, I

and Q outputs are squared and summed, and the square root

is taken of the sum.

Click for high-quality image

All of the foregoing computations—a total of eight for

each pair of numbers that is input plus four for the filter

output—must be repeated for every filter that is formed. If

32 pairs of numbers are integrated, this amounts to a total

of (8 x 32) + 4 = 260 computations per filter. If, as in the

earlier example, returns from 100 range intervals are

processed, a total of 260 x 100 = 26,000 computations

must be performed for just this one frequency during every

integration time.

Sidelobe Reduction

As was illustrated in Fig. 14, the passband of a digital fil-

ter has sidelobes similar to the sidelobes of a linear array

antenna. Unless something is done to reduce these, a tar-

get’s echoes may be detected in the outputs of several adja-

cent doppler filters, or, if the echoes are especially strong,

in the outputs of a considerable portion of the filter bank.

Fortunately, filter sidelobes yield to the same reduction

technique as antenna sidelobes. (This technique was

described in Chap. 18.) Just as antenna sidelobes are due

to the radiation from the radiators at the ends of the array,

filter sidelobes are due to the pulses at the beginning and

end of the pulse train. By progressively reducing the ampli-

tudes of these pulses, the spectral sidelobes can be substan-

tially reduced.

This process, called amplitude weighting, is carried out

“wholesale,” before the digitized video is supplied to the

doppler filters (Fig. 22). Following every transmission, the

numbers representing the I and Q components of the

return from each range increment are multiplied by a

weighting coefficient. The coefficient is changed from one

pulse to the next according to a prescribed pattern, which

CHAPTER 19 How Digital Filters Work

263

22. Outputs of A/D converter are multiplied by weighting coeffi-

cients before being supplied to doppler filters.

ALGORITHM FOR APPROXIMATING

Although it looks simple enough, taking the vector sum,

公

—

⫹ J

is a comparatively long process. For the square root

can be found only through an iterative series of trials.

To save computing time, therefore, the value of

公

—

⫹ J

commonly approximated. The simplest of several possible

algorithms for making this approximation is this:

• Subtract I from J (or vice versa) to find which is smaller.

• Divide the smaller quantity by two. (Doing this in binary

arithmetic is easy: you just shift the number right one binary

place.)

• Add the result to the larger quantity. The sum is

⬃

公

—

⫹ J

The error of approximation varies with the value of the phase

But at most it is only a fraction of a decibel.

Click for high-quality image

PART IV Pulse Doppler Radar

264

is repeated for each train of pulses that is to be integrated. If

this pattern has been suitably selected, the sidelobes can be

reduced to an acceptable level. In the process, the passband

is widened somewhat just as the mainlobe of an antenna is

widened by illumination tapering. But this is generally a

small price to pay for the reduction achieved in the side-

lobes.

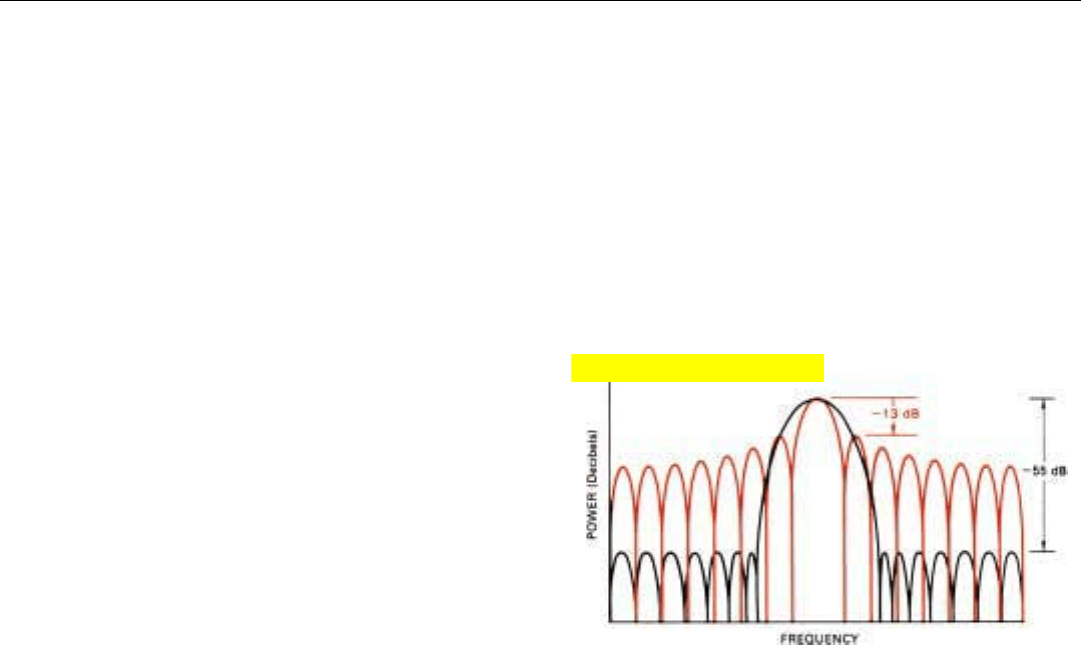
What is an acceptable sidelobe level? Naturally this

depends upon the application. The characteristic of a

weighted filter for a representative fighter application is

shown in Fig. 23.

Incidentally, even when a doppler filter’s sidelobes have

been acceptably reduced, some return will invariably get

through the sidelobes. If strong enough, therefore, return

that is outside a filter’s passband can still be detected in the

filter’s output.

For this reason, it is essential that strong ground return

be filtered out before the radar return is applied to a bank of

doppler filters.

Filtering Actual Signals

In the foregoing discussion, we considered a somewhat

artificial situation in which the numbers supplied to the fil-

ter represented a continuous train of echoes from a single

target and nothing more. How, you may ask, does the filter

respond in the real world, where echoes may be received

simultaneously from more than one target, where a target’s

echoes may be accompanied by strong ground return, and

where sometimes there may be no echoes at all, only noise?

Let us assume that the radar receiver and signal proces-

sor are reasonable “linear” and (as discussed in Chap. 18)

saturation has been avoided in all stages of receiving and

signal processing up to the filter. The input to the filter then

will simply represent the algebraic sum of the instantaneous

23. Reduction in sidelobe level achieved by weighting the inputs to

a representative doppler filter. Note broadening of passband.

Click for high-quality image