George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

values of all of the simultaneously received signals, multi-

plied of course by the system gain up to that point. If the

filter itself doesn’t saturate—i.e., if the integrated signal

doesn’t “overflow” the filter’s registers—the output will be

the same as if each of these signals had been integrated

individually and the individual outputs had then been

superimposed.

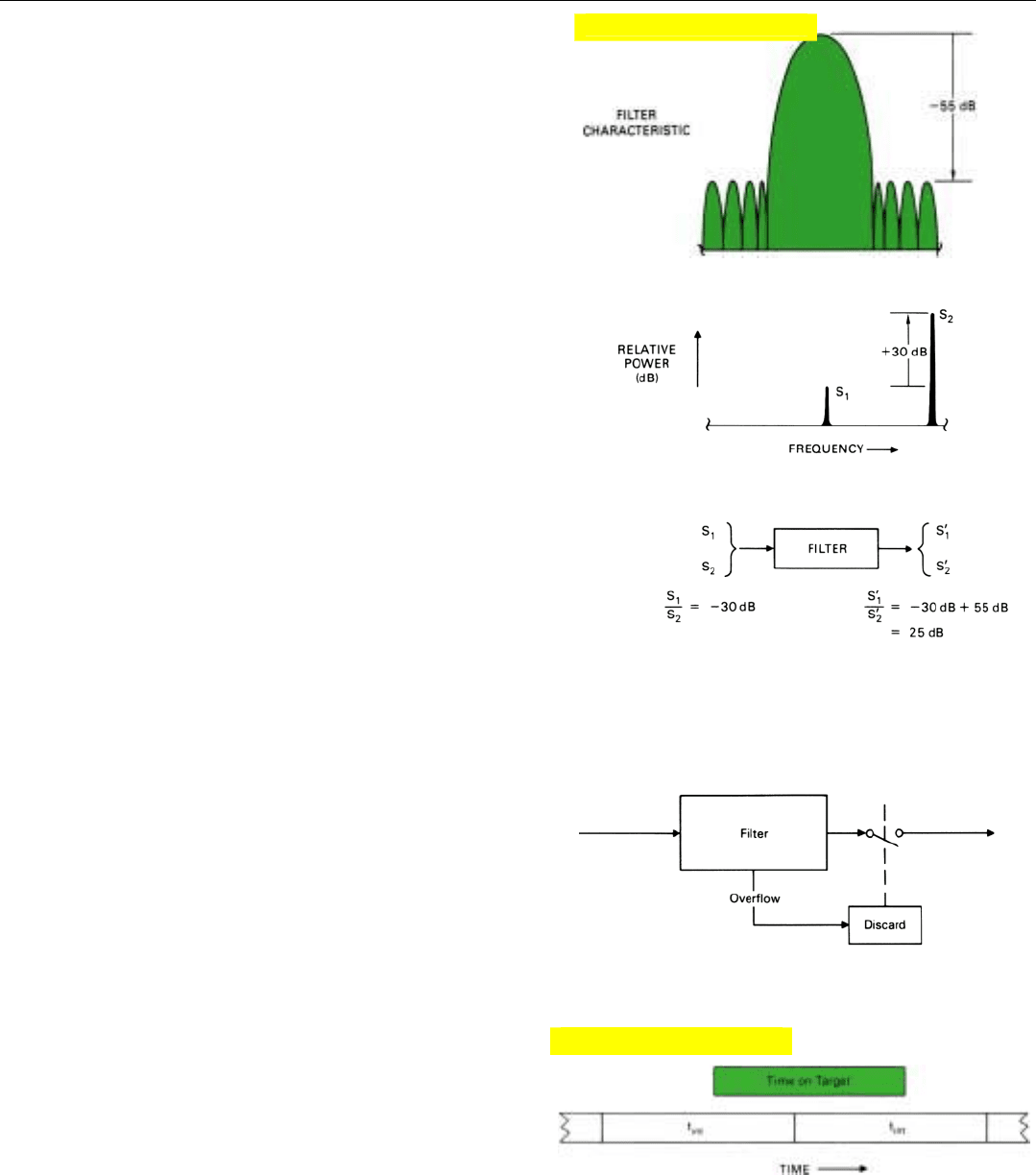
Suppose, for example, that the doppler frequency of a

given signal, S

, lies in the center of the filter’s passband

and the doppler frequency of a stronger signal, S

, lies out-

side (Fig. 24). The ratio of the outputs produced by the two

signals will equal the ratio of the powers of the two signals

times the ratio of the filter’s gain at its center frequency to

its gain at the frequency of S

. If, say, S

is 30 dB stronger

than S

but the filter’s gain at S

’s frequency is down 55 dB

from the gain at the center of the passband, the output pro-

duced by S

will be 55 dB – 30 dB + 25 dB stronger than

the output produced by S

. The outputs would be exactly

the same as if the two signals had been received at different

times.

And noise? As explained in Chap. 10, depending upon

its relative phase, noise falling in the filter passband may

combine with a target signal either destructively or con-

structively or somewhere in between. As a result, the filter

output produced by an otherwise detectable target may

sometimes fail to cross the detection threshold, and vice

versa. At times, too, the integrated noise alone may exceed

the threshold.

What if the filter saturates? That, too, is possible. To

avoid making errors when this happens, the signal proces-

sor is usually designed to sense overflows in a filter’s regis-

ters and discard the filter output when they occur (Fig. 25).

One more question: What if the reception of a train of

target echoes is not synchronized with the filter’s integration

period? Suppose the first echo of the train is received half

way through t

int

Synchronization between the radar antenna’s time-on-

target and the integration time of the doppler filters is, of

course, entirely random. The first pulse in a train of target

echoes is as likely to arrive in the middle of the integration

period as at the beginning (Fig. 26). Consequently, on an

average, the integrated signal in the output of the filter gen-

erally falls short of the maximum possible value. In calcu-

lating detection probabilities, this difference is normally

accounted for by including a loss term in the range equa-

tion (see Chap. 11).

All told, though, performance of a digital filter in a real

life situation is very much as has been described here. If

saturation has been avoided and strong ground return has

CHAPTER 19 How Digital Filters Work

265

25. If an overflow occurs in a filter’s registers, it will be sensed

and filter output will be discarded.

26. Synchronization of antenna’s time on any one target and

filter’s integration time (t

int

) is completely random.

24. What happens when two signals (S

and S

) of different fre-

quency are simultaneously applied to a filter tuned to the fre-

quency of S

. Although S

is only

/1000th as strong as S

the output produced by S

will be 25 dB stronger.

Click for high-quality image

PART IV Pulse Doppler Radar

266

largely been rejected in advance, a well designed digital fil-

ter will separate target echoes from clutter and noise on the

basis of their differences in doppler frequency, quite as

effectively as a well designed analog filter.

Summary

A digital doppler filter receives as inputs a succession of

pairs of digital numbers. If echoes from a target are being

received, each pair constitutes the x and y components of a

phasor representing one sample of a signal whose ampli-

tude corresponds to the power of the target echoes and

whose frequency is the target’s doppler frequency. The job

of the filter is to integrate these numbers in such a way that

if the doppler frequency is the same as the filter’s frequency,

the sum will be large but otherwise it will not.

In essence, the filter projects successive x and y compo-

nents onto a coordinated system that rotates at the frequen-

cy the filter is tuned to and sums the components separate-

ly. At the end of the integration period, the magnitude of

the integrated signal is computed by vectorially adding the

two sums. The simple algorithm which must be repeatedly

computed to perform the integration and obtain the magni-

tude of the vector sum is called the discrete Fourier trans-

form (DFT).

A plot of the filter output versus doppler frequency for a

pulse train of given length and power has a sin x/x shape.

Its peak value is proportional to the total energy of the

pulse train. Its nulls occur at intervals equal to 1/t

int

either side of the central frequency.

To reduce the sidelobes of this pattern, the numbers rep-

resenting the pulses at the beginning and end of the train

are progressively scaled down—a process called amplitude

weighting.

Barring nonlinearities and saturation, when several sig-

nals are received simultaneously, the filter output is the

same as if the signals had been integrated separately and

the results had been superimposed. Since receipt of a train

of pulses cannot be synchronized with the filter’s integra-

tion time, the filter output is on an average less than the

potential maximum value.

Some Relationships To Keep In Mind

• Filter passbands:

Null-to-null =

Between half power points =

where t

int

= filter integration time)

• Operations per sample required to form a filter

with the DFT

Multiplications = 4

Additions = 4

• Operations required to approximate I

+ J

Subtractions = 1

Division by 2 = 1

Additions = 1

int

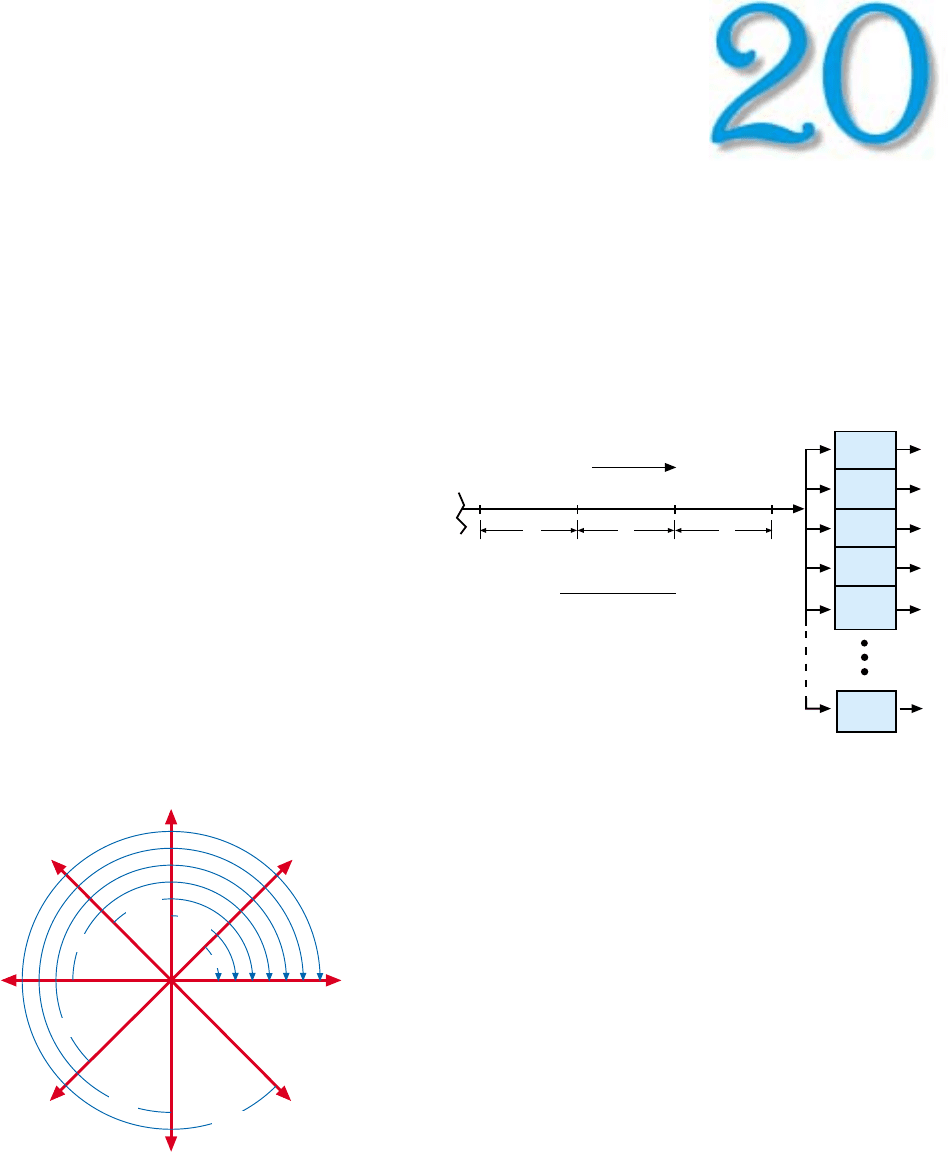
267

The Digital Filter Bank

and the FFT

1. Digital filter bank. I and Q components of successive sam-

ples of the receiver output are applied in parallel to N

digital filters. Filter F

passes dc . Filters F

, F

, etc.

are tuned to progressively higher frequencies.

n Chaps. 18 and 19, we learned that the simultaneous-

ly received returns from several different targets may

be sorted in accordance with the targets’ doppler fre-

quencies by applying the I and Q components of suc-

cessive samples of the receiver output from the same range

to a bank of digital filters (Fig. 1). With the aid of phasor

diagrams, we saw that a digital filter achieves its selectivity

by rotating the phases of successive samples through pro-

gressively larger angles proportional to the desired filter fre-

quency and summing the rotated samples

(Fig. 2). This iter-

ative process, we learned, is performed with an algorithm

called the discrete Fourier transform (DFT).

2. Phase rotations which a digital filter must perform to bring succes-

sive samples—a

, a

, etc.—of a signal having a given doppler

frequency into phase with the first sample, a

. Sample-to-sample

phase advance due to a positive doppler shift (closing target) is

counterclockwise. The phase rotations needed to remove these

advances, are clockwise.

N - 1

T =

Sampling Rate

, q

Samples

i = In-Phase Component

q = Quadrature Component

∆ = 2π f T

f = frequency of signal

T = sampling interval

1∆

= sample n

4∆

3∆

2∆

5∆

6∆

7∆

PART IV Pulse Doppler Radar

268

For forming a single filter, the DFT is quite efficient.

Only eight simple arithmetic operations must be per-

formed per sample (Fig. 3). But if the number of samples

and the number of filters per bank are large, and, if filter

banks are needed for many successive range increments,

forming the filters with the DFT requires an immense

amount of processing. Moreover, if the filters must be

formed in real time—that is, if all of the computations per-

formed on one set must be completed before the processor

receives the next set of samples from the radar—an excep-

tionally high processing throughput is required (Fig. 4).

In this chapter, we will see how the required throughput

may be dramatically reduced by forming each filter bank

with an algorithm called the fast Fourier transform (FFT).

Following a brief overview of the basic concept, we’ll

examine the FFT for a small filter bank; then, see how its

design may be extended to banks of virtually any size.

Finally, we’ll derive a simple rule of thumb for quickly esti-

mating the amount of processing needed to form a filter

bank with the FFT—as opposed to the DFT— and get a

feel for the rapid increase in the FFT’s processing savings

with the size of the bank.

Basic Concept

The efficiency of the FFT is achieved in two basic ways.

First, the key parameters of the bank are selected so that

the phase rotations applied to successive samples to form

successive filters are harmonically related. Second, the

phase rotation and summation of samples for all of the fil-

ters are consolidated into a single, multi-step process

which exploits these harmonic relationships to eliminate

duplications that occur when the filters are formed individ-

ually. To illustrate, let us consider a representative FFT.

A Representative FFT

Over the years, many different versions of the FFT have

evolved. The basic principles underlying them all, howev-

er, are most simply illustrated by the original Cooley-Tukey

algorithm.

For it, the parameters of the filter bank are selected in

accordance with these rules.

• Make the number of filters (N) equal to a power of

two—e.g., 2, 4, 8, 16, 32, 64, 128, 256, 512, etc.

• Form each filter by summing N successive samples.

• Make the incremental phase rotation, ∆

, for the low-

est-frequency filter (F

) equal to 360°÷ N.

• Make the incremental phase rotations for successive

filters whole multiples of ∆

(see Fig. 5, next page).

3. The discrete Fourier transform (DFT). The iterative equations

for forming a single digital filter from the in-phase and quad-

rature components of a sequence of discrete samples of a con-

tinuous wave require performing eight simple computations

per sample.

4. Digital computation which would be needed to satisfy even a

simple radar signal processing requirement if the filters are

formed individually with the DFT. To do the processing in real

time, all of the computations must be completed by the time

the radar has taken the next set of samples.

Conditions

Samples summed per filter (S) . . . .. . . . . . . 16

Filters formed per bank (F) . . . . . . . . . . . . . . 16

Simultaneously formed filter banks (B) . . . 100

Computations per sample for DFT (C

) . . . . 8

Sampling rate (f

) . . . . . . . . . . . . . . . . . . 10 MHz

Computations Required to Form the Banks (C

)

= S x F x B x C

= 16 x 16 x 100 x 8

= 204,800 operations

Required Processor Throughput (P

)

x (f

÷ S)

= 204,800 x (10

÷ 16)

= 1.28 x 10

computations per second

SIMPLE FILTERING REQUIREMENT

Form 16-filter banks from radar returns stored in

each of 100 range bins

DFT

I = i

cos n ∆θ + q

sin n ∆θ

Q = q

cos n ∆θ – i

sin n ∆θ

n = 0

N – 1

n = 0

N – 1

∆θ = 2π f T

= in-phase component of sample n

= quadrature component of sample n

n = sample number (0, 1, 2, . . . (N -1)

f = desired frequency of filter

T = time between samples

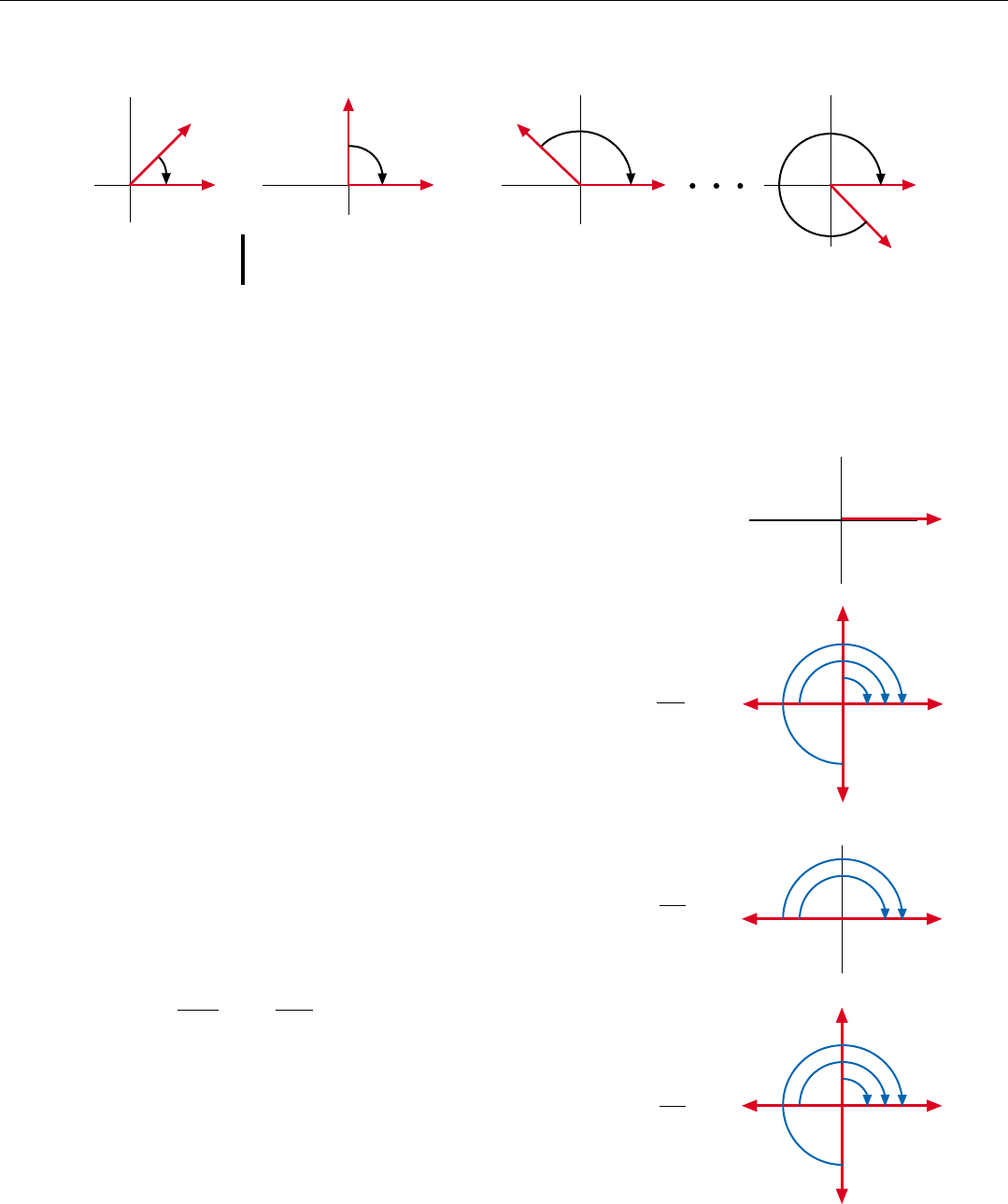
This choice of parameters leads to a high degree of sym-

metry throughout the bank and results in all of the phase

rotations applied by the filters being multiples of ∆

Consequently, the samples can be partially summed for

more than one filter at a time, and the required phase rota-

tions can be incrementally applied to both the individual

samples and the partial sums.

Just how this is done may be most easily seen by consid-

ering the FFT for a four-filter bank. While such a bank may

seem trivially small, the FFT for it is simple to describe and

suffices to illustrate virtually all of the fundamental features

of the algorithm for any sized bank.

Required Phase Rotations. The phase rotations needed

to form our four filter bank are illustrated in Fig. 6. The

phasors in the diagram for each filter represent successive

samples of a continuous wave whose frequency is to be

passed by that particular filter. The curved arrows indicate

the phase rotations necessary to bring all of the samples

into phase, so they will produce the maximum possible

output when summed.

The incremental phase rotation for Filter 1 is 90 degrees.

∆

360°

= 90°

The incremental phase rotations for Filter 2 and Filter 3

are integral multiples of ∆

: 2∆

and 3∆

For Filter 0, of course, none of the samples are rotated.

For Filter 2, sample a

also is not rotated, and samples a

and a

are both rotated by 2∆

. For Filter 1 and Filter 3,

sample a

also is rotated by 2∆

The way in which the FFT takes advantage both of these

duplications and of the harmonic nature of the phase rota-

tions is most clearly illustrated by the processing flow dia-

gram for the algorithm.

CHAPTER 20 The Digital Filter Bank and the FFT

269

5. Incremental phase rotations for an eight-filter bank whose parameters are selected for implementation with the Cooley-Tukey FFT. This selection

results in all phase rotations being harmonically related. (Filter 0, which sums samples of constant phase (dc) requires no phase rotations.)

6. Phase rotation and summation requirements for a four-filter

bank. The phasor diagram for each filter illustrates the

required phase rotations of successive samples of a wave

whose frequency is to be passed by the filter.

INCREMENTAL PHASE ROTATIONS

∆

2 ∆

FILTER 1

FILTER 2

FILTER 3

360°– ∆

FILTER (N – 1)

3 ∆

Conditions

Number of filters: N = 2

(n = 1, 2, 3 . . . )

Number of samples = N

∆ = 360° ÷ N

is sample 0.

is sample 1.

␪

Sampling Frequency = f

FILTER 1

FILTER 0

= 0

= 1

FILTER 2

= 2

FILTER 3

= 3

Incremental

rotation = 2 ∆

Incremental

rotation = 3 ∆

Incremental

rotation = ∆

␪

PART IV Pulse Doppler Radar

270

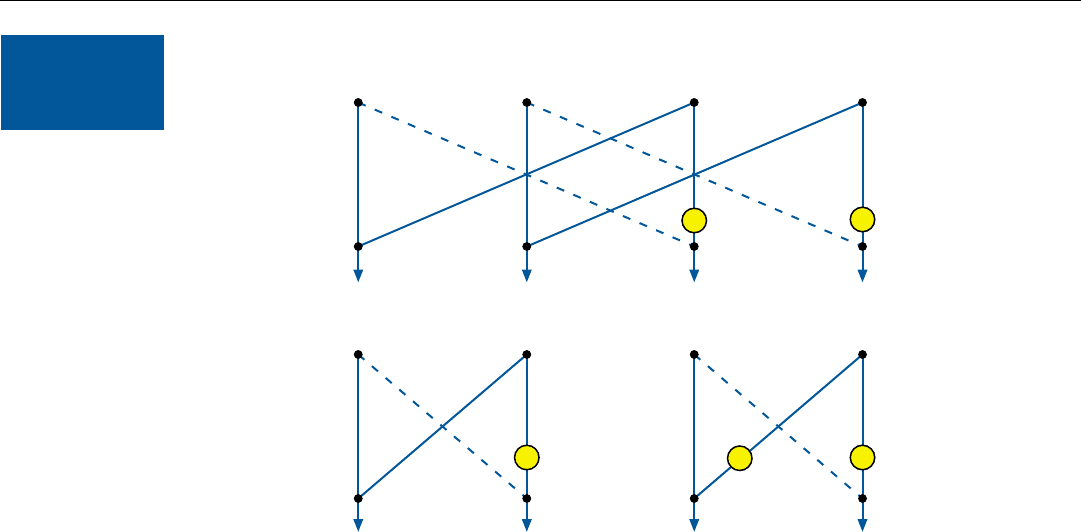
Processing Flow Diagram. The flow diagram for the

bank is shown in Fig. 7. Before discussing it, however, the

conventions used in plotting the flow may warrant some

explanation.

• The numbers at the top of the diagram identify mem-

ory locations in the signal processor. For reasons

which will become clear later on, these “addresses”

are written in binary form.

• The lowercase letters—a

, a

, and a

—represent

the samples to be summed. Each stands for a com-

plex number specifying the amplitudes of the sam-

ple’s i and q components (see inset).

• The vertical and slanted lines indicate the flow of

these numbers. To avoid confusion where the lines

cross, those lines slanting to the right are dashed.

• At the points where the lines meet, the I and Q com-

ponents of the complex quantities they represent are

separately summed.

• Each circled number represents a phase rotation. The

number indicates what multiple of the incremental

rotation, ∆

, is applied. A circled 3, for example,

indicates a rotation of 3∆

7. FFT flow diagram for a four-filter bank. The circled numbers represent multiples of the basic phase increment, ∆θ. By convention, in the lists

of samples included in the sums, these numbers are shown as powers of the complex operator, W.

00 01 10 11

+ a

+ (a

+ a

+ (a

+ a

+ (a

+ a

Addresses

Samples

STEP 2

Filters

Numbers

Final

Sums

+ a

STEP 1

Partial

Sums

= i

+ jq

∆ = 90°

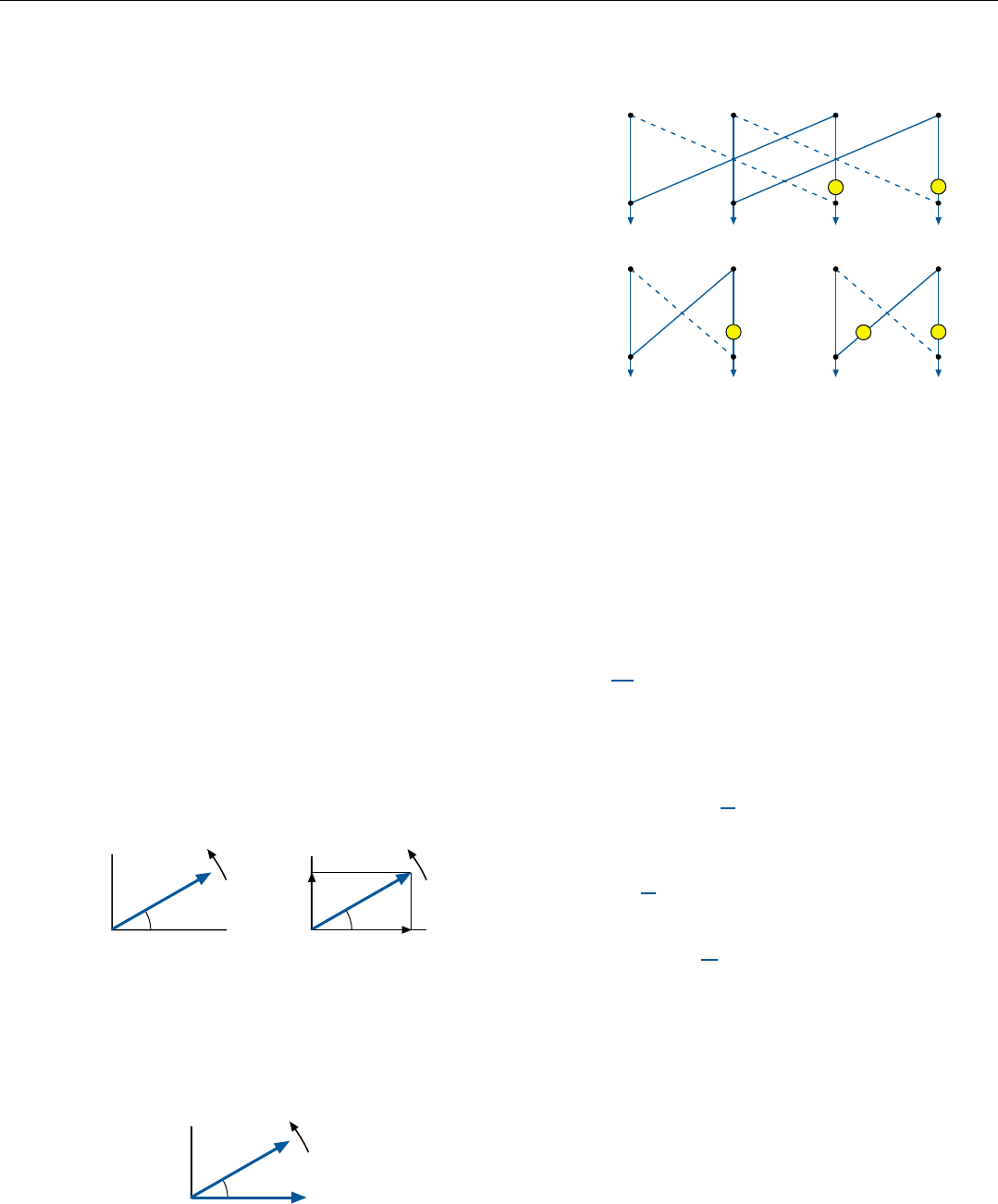
When all four samples needed to form the filter bank

have been received and placed in the assigned memory

locations, two major processing steps are performed.

In Step 1 (see repeat of Fig. 7, right), each sample has

added to it the sample that is two memory locations away

and is returned to its original location. Before this addition

is made to the samples in memory locations 10 and 11, their

phases are rotated by 2∆

. For your convenience, beneath

each summation point, the samples included in the

sum are

listed. By convention, in these lists the phase rotations are

indicated as powers of the operator W. For example,

stands for a phase rotation of 2∆

. (See the panel below.)

In Step 2, each of the partial sums produced in Step 1

similarly has one of the other partial sums added to it. In

this case, though, the sums that are added are taken from

adjacent memory locations. Again, below the summation

points, the compositions of the sums are listed. Each of

these sums includes all four samples.

Referring back to Fig. 6, you will see that these sums

meet the requirements of each of the four filters. The sum

CHAPTER 20 The Digital Filter Bank and the FFT

271

–

jωt

= a

–

f n

2π

THE COMPLEX OPERATOR W

In this chapter, the DFT is conveniently expres-

sed in terms of the complex operator, W, rather than

sine and cosine functions. If you are unfamiliar with

complex notation, you may find correlating the two

methods of expression illuminating.

The panel on page 69 explained how the ampli-

tude and phase of a sinusoidally varying signal

represented by a phasor may be mathematically

expressed as an exponential function.

When either of the above functions is used to

represent one of N

discrete

samples of a signal, t is

the period between the time sample a

was taken

and the time the first sample in the series, a

, was

taken. The product,

ωt, then is the phase angle, θ

of a

relative to a

As explained in the text, in a digital filter bank,

is equal to the basic phase increment for the

bank,

∆θ, times the filter number, f, times the

ωt = θ

By (a) substituting this term for ωt in the expo-

nential expression for the sample and (b) reversing

the algebraic sign of j to indicate a clockwise phase

rotation that will bring a

into phase with a

, we get:

Now, the operator W is a shorthand represen-

tation of the non-varying portion of the exponential.

Expressed in terms of W, the exponential func-

tion can be mathematically manipulated, like any

other constant raised to a given power.

W = e

- j

2π

Consequently,

f r

= a

- j

f r

2π

(a + b)

= W

= 1 and a W

= a

The exponent applied to W indicates phase rotation

in multiples of

∆θ. For example,

= a phase rotation of 4 ∆θ

Since ∆θ = 2π/N, a rotation of N∆θ is 2π radians,

or 360°. Thus,

ωt = f n

2π

sample number, n. For the FFT, ∆θ = 2π/N. Thus,

a e

jωt

ωt

a (cos ωt + j sin ωt)

(mN)

= W

m = 1, 2, . . .

(N + m)

= W

00 01 10 11

+ a

+ (a

+ a

+ (a

+ a

+ (a

+ a

Addresses

Samples

STEP 2

Filters

Numbers

Final

Sums

+ a

STEP 1

Partial

Sums

9. Eliminating a phase rotation by taking advantage of the har-

monic nature of the rotations. In this example, 2∆

= 180˚.

Consequently, by moving the rotation of 1∆

, shown in (a),

ahead of the branch in the flow diagram, the rotation of 3∆

in the right-hand branch can be reduced to 2∆

, as in (b), and

replaced with a simple change in algebraic sign, as in (c).

PART IV Pulse Doppler Radar

272

stored in memory location 00 satisfies the requirement for

Filter 0 (which passes dc): none of the samples are rotated.

The sum in memory location 01, satisfies the phase rota-

tion requirements of Filter 2. The sum in memory location

10 satisfies the requirements of Filter 1. And the sum in

memory location 11, satisfies the requirements of Filter 3.

Reduction in Computations. A count of computations

indicated in the flow diagram of Fig. 7 reveals that, for this

small filter bank, the FFT has reduced the number of com-

plex additions from 16—which would have been required

if the filters were formed individually with the DFT—to 8.

And it has reduced the number of phase rotations from 16

to only 5. Even so, the harmonic relationship of the phase

rotations can be further exploited in two basic ways to

reduce the required number of phase rotations still more.

First, a phase rotation of (N/2) x ∆

= 180°. The equiva-

lent of that rotation can be achieved simply by giving the

quantity whose phase is to be rotated a negative sign

(Fig. 8). For this four-filter bank, N/2 = 2; hence, a rota-

tion of 2∆

= 180°. Consequently, in Step 1 the phase

rotations of 2∆

applied to samples a

and a

can be elimi-

nated by changing their algebraic signs. So can the phase

rotation of 2∆

applied in Step 2 to the partial sum in

memory location 01. The number of phase rotations may

thus be reduced from 5 to 2.

Second, in Step 2, the partial sum stored in memory

location 11 is rotated by 1∆

before being added to the

sum in memory location 10 and by 3∆

before the sum in

memory location 10 is added to it. A rotation of 3∆

equals a rotation of 1∆

+ 2∆

. Consequently, by applying

the 1∆

rotation to the sum residing in memory location

11 before it is included in the two following summations,

the 3∆

rotation can be replaced with a 2∆

rotation, and

it in turn can be replaced with a change in algebraic sign

(Fig. 9, below).

8. A phase rotation of 180˚—represented by W

in this chap-

ter‘s four-filter example—can be eliminated simply by chang-

ing the algebraic sign of the complex number representing the

sample (or partial sum) whose phase is to be rotated.

– a

180°

a W

– a W

1 1

(–)

(a) (b) (c)

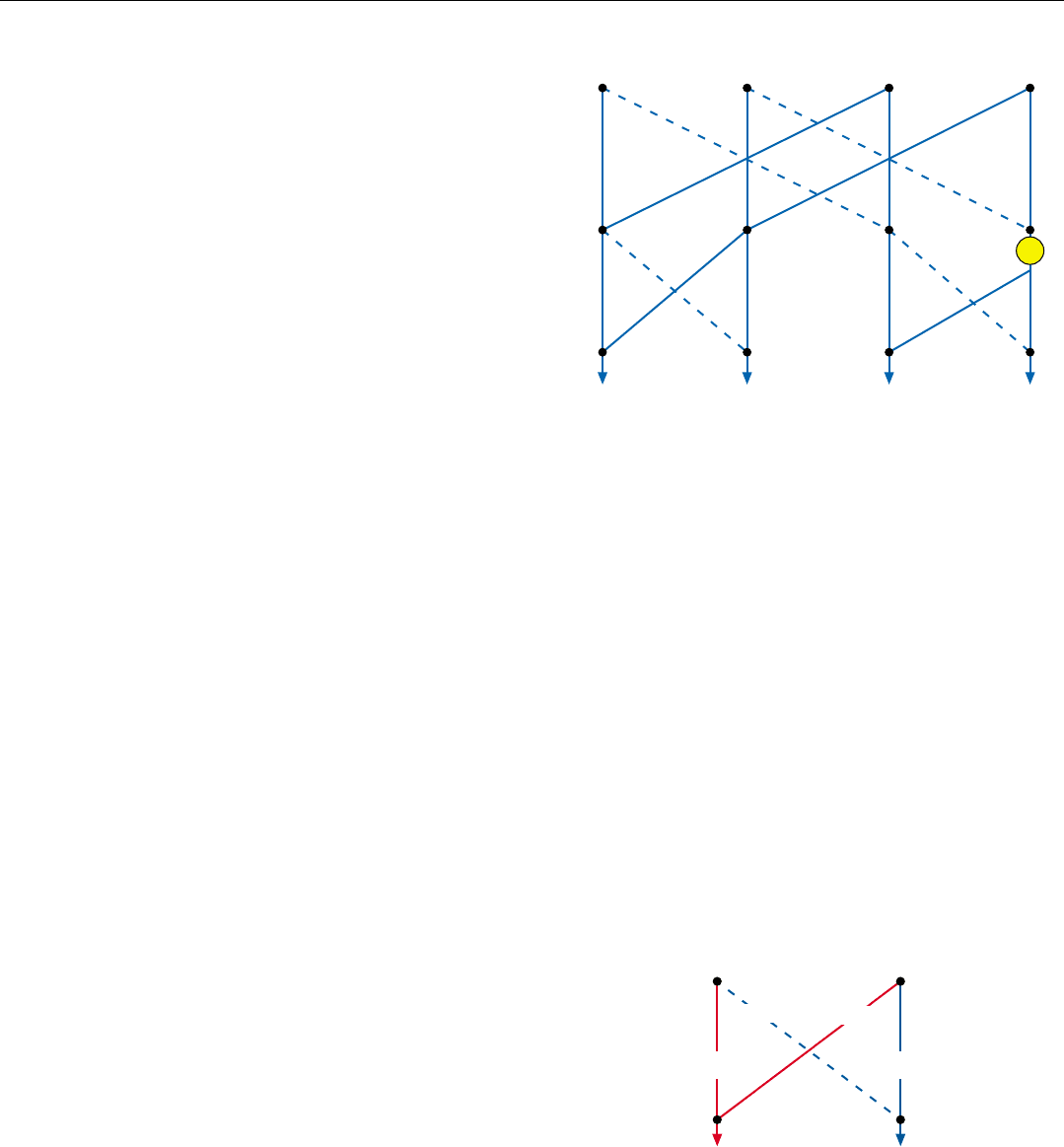
With these changes, the required number of rotations is

reduced to only 1 (Fig. 10).

From the flow diagram for this small filter bank, four

significant conclusions may be drawn regarding the FFT

for any sized bank.

• In each step of processing, N summations are per-

formed, in which two complex numbers are alge-

braically added.

• In general, before each addition is performed, the

phase of one of these numbers must be rotated. But

half of these rotations can be eliminated through a

change in algebraic sign. And no rotations are

required for the first step.

• In each successive step, the number of samples

included in every sum is doubled. Since N is a power

of 2, all N samples can be summed for each of the N

filters in log

N steps, thereby substantially reducing

the number of summations as well as the number of

phase rotations required.

• No intermediate results need to be saved; the final

sums for the N filters end up residing in the same

memory locations as were initially occupied by the N

samples from which the filters were formed.

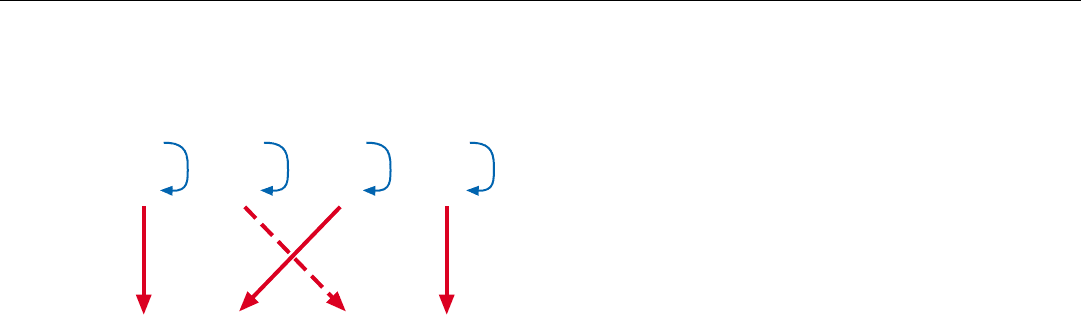
Rotating the Phases. While the flow diagram specifies

the required amount of each phase rotation, it doesn’t

illustrate how the rotation is produced. Actually, there is

no reason to do so. For all of the rotations are produced

with the same two simple equations as are used to rotate

the phase of a single sample in the DFT:

= i

cos n∆

+ q

sin n∆

= q

cos n∆

– i

sin n∆

where i

and q

are the in-phase and quadrature compo-

nents of the complex number whose phase is to be rotated,

n∆θ is the desired amount of rotation, and i

and q

are

the in-phase and quadrature components of the number

after rotation. Figure 11 presents the processing flow dia-

gram for this single complex multiplication.

Identifying the Filter Outputs. As you may have noticed

in Figs. 7 and 10, although the filter outputs do indeed

occupy the same memory locations as were initially occu-

pied by the samples from which the filters were formed,

the outputs are not all in the same numeric order. The out-

put of filter F

ends up in the location initially occupied by

CHAPTER 20 The Digital Filter Bank and the FFT

273

10. FFT flow diagram for the four-filter bank after simplification.

By (1) replacing phase rotations of 2∆θ with changes in alge-

braic sign, (2) replacing the phase rotation of 3∆θ with the

already required rotation of 1∆θ (for filter F

), and (3) chang-

ing the algebraic sign at the bottom of the far right leg of the

diagram, the required number of rotations has been reduced

to only one.

00 01 10 11

(–)(–)

(–)

11.

Phases are rotated with the same equations (one complex multi-

ply) as used to rotate the phase of a single sample with the

DFT.

= i

(cos n∆ ) + q

(sin n∆ )

= q

(cos n∆ ) – i

(sin n∆ )

cos n∆

sin n∆

(–)

sin n∆

PART IV Pulse Doppler Radar

274

sample a

; and the output of filter F

, in the location ini-

tially occupied by sample a

. We identified the outputs by

correlating them with the phasor diagrams for the filters.

While that was easily done for our small four-filter bank, it

is not convenient for larger banks.

It turns out that, because of the binary nature of the

algorithm, you can tell which memory locations the out-

puts occupy simply by writing the filter numbers in binary

form and reversing the order of the digits—last digit first,

first digit last—as illustrated in Fig. 12.

Forming Magnitudes. As with the DFT, the final step in

forming a filter bank with the FFT is combining the I and

Q components of the final sum for each filter. As we saw

in Chap. 19, the components may be combined either by

taking the square root of the sum of their squares or by

executing a more easily computed algorithm, such as that

presented on page 263.

In some cases, it is desired to further process a filter

bank’s outputs before the phase information implicit in the

I and Q components is lost. This last step may then be

postponed.

FFTs for Filter Banks of Any Size

In practice, filter banks containing many more than

four filters are generally required. Following the same

basic approach as outlined above, FFTs may be designed

for filter banks of virtually any size. The first step, of

course, is determining what phase rotations must be per-

formed.

Determining the Required Phase Rotations. For banks

of four, or even eight filters, the required phase rotations

can be determined on sight, as we just have done, from

phasor diagrams for the individual filters. But for larger

banks, the rotations are best determined mathematically.

The panel on the next page presents a simple math-

ematical derivation of the original Cooley–Tukey FFT for

an eight-filter bank. The derivation begins with the equa-

tion for forming the eight filters directly with the DFT—

expressed in terms of the complex variable, W. The filter

and sample numbers in this equation are then expanded in

binary form, phase rotations of 360° and multiples thereof

are eliminated, and the summation is carried out separate-

ly for each binary digit. A series of recursive equations is

thus produced which specifies the phase rotations and

summations to be performed in each of the FFT’s log

processing steps.

Following that general procedure, computer programs

can readily be written with which the FFT for any sized fil-

12. Simple procedure for identifying the memory locations of the

filter outputs. Write each filter number in binary form and

reverse the order of the bits—last bit first, first bit last. The

result is the address of the filter

‘

s output.

Filter

Outputs

00 01 10 11

Memory

Addresses

Filter

Numbers

(00)

(01) (10) (11)

Bit-Order

Reversed

(00) (10) (01) (11)