George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

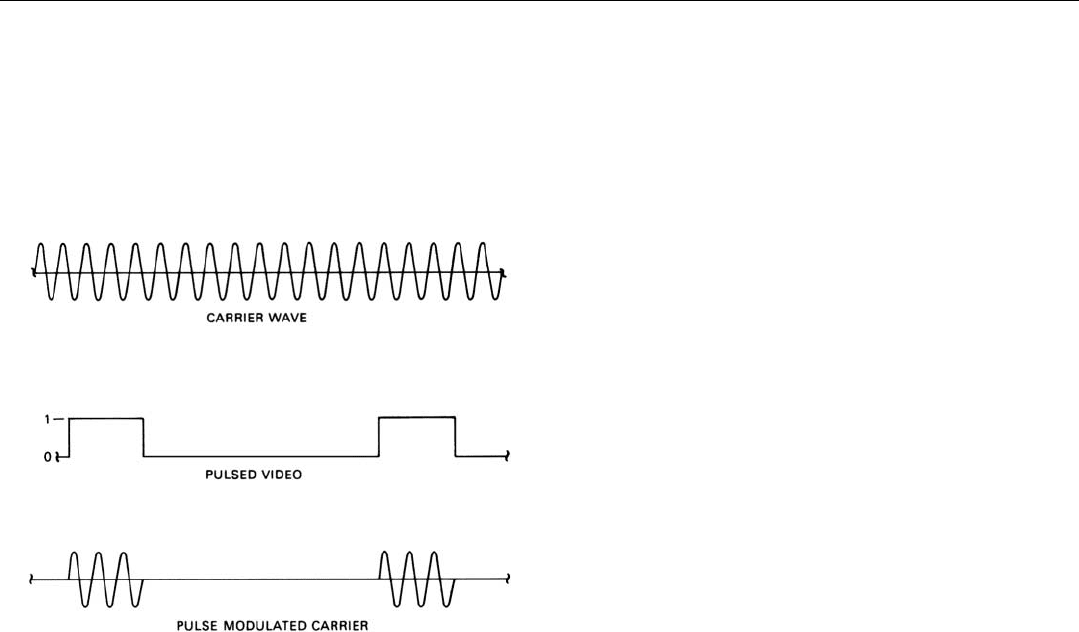
Although not generally thought of in this way, a pulsed

radio wave, such as is transmitted by a radar, is actually a

continuous wave (carrier) whose amplitude is modulated by

a pulsed video signal. The latter has an amplitude of one

during each pulse and zero during the periods between

pulses (Fig. 11).

As we learned in Chap. 5, any wave whose amplitude is

modulated invariably has sidebands, and a portion of the

wave’s energy is contained in each of these. (The signal of an

AM broadcast station is an example.)

So one way of explaining how the energy of a pulsed

radio wave is distributed in frequency is to visualize the

spectrum in terms of the sidebands produced by a pulsed

modulating signal. Fortunately, we can determine the

nature of the sidebands quite easily, with the help of the

Fourier series.

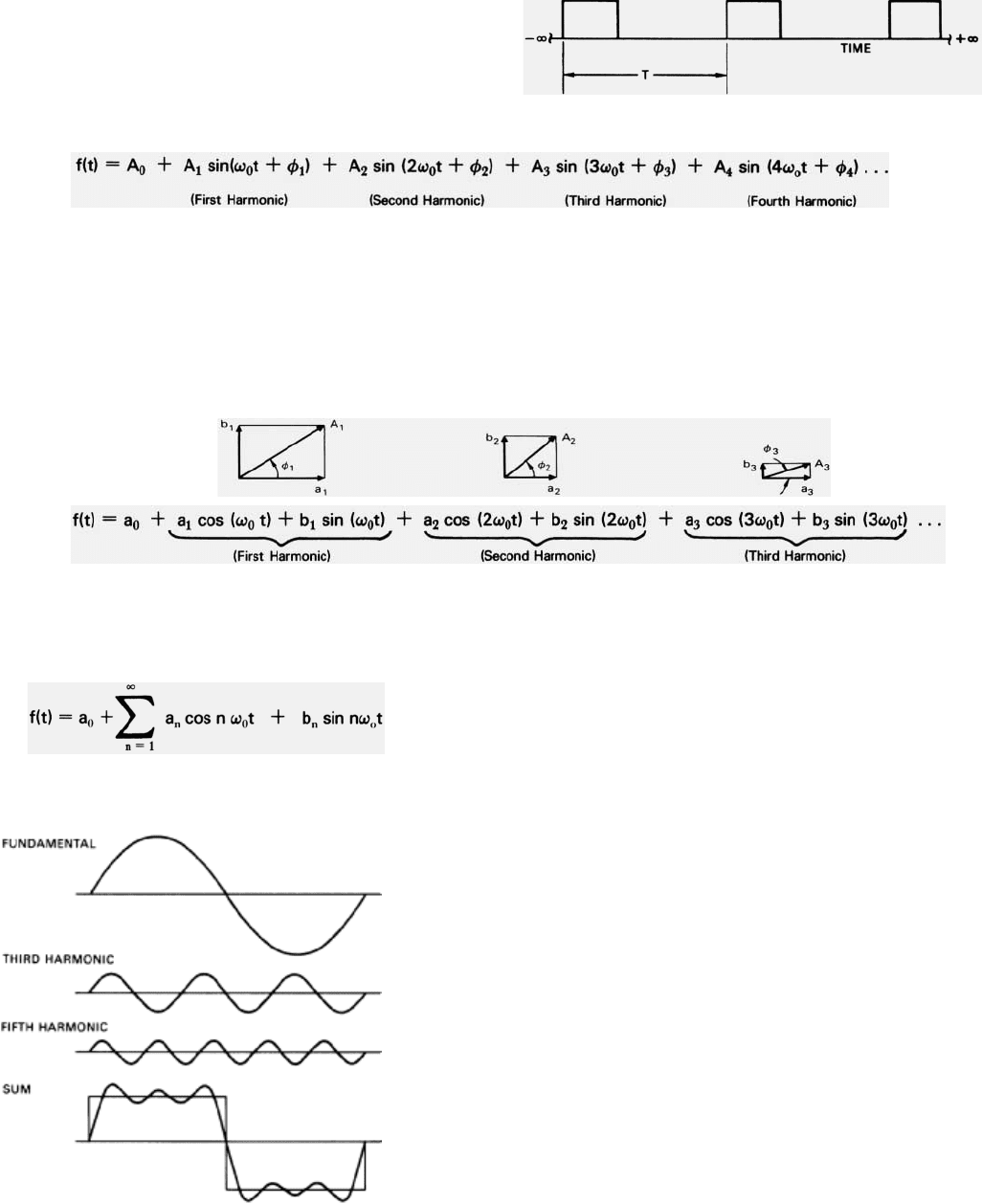
Fourier Series

It can be demonstrated both graphically and mathemati-

cally that any continuous, periodically repeated wave shape,

such as the pulsed modulating signal just referred to, can be

created by adding together a series of sine waves of specific

amplitudes and phases whose frequencies are integer multi-

ples of the repetition frequency of the wave shape. The repe-

tition frequency is called the fundamental; the multiples of it

are called harmonics. The mathematical expression for this

collection of waves is the Fourier series. (See panel at top of

next page.)

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

213

11. A coherent pulsed radio-frequency signal is actually a continu-

ous wave (carrier) whose amplitude is modulated by a pulsed

video signal.

PART IV Pulse Doppler Radar

214

Application to Rectangular Waves. The concept is illus-

trated graphically for a square wave in Fig. 12.

As you can see, the shape of the composite wave

depends as much upon the phases of the harmonics as

upon their amplitudes. To produce a rectangular wave, the

phases must be such that all harmonics go through a posi-

tive or negative maximum at the same time as the funda-

mental.

A wave of a more general rectangular shape is illustrated

in Fig. 13 at the top of the facing page.

Theoretically, to produce a perfectly rectangular wave an

infinite number of harmonics would be required. Actually,

the amplitudes of the higher order harmonics are relatively

small so reasonably rectangular wave shapes can be pro-

duced with a limited number of harmonics. For example, a

recognizably rectangular wave has been produced in Fig. 12

by adding only two harmonics to the fundamental.

12. Square wave produced by adding two harmonics to the fun-

damental. (Because positive and negative excursions are of

equal duration, amplitude of even harmonics is zero.)

THE FOURIER SERIES

Any well-behaved periodic function of time, f(t), that can be

assumed to continue from the beginning to the end of time can be

represented by the sum of a constant, a

, plus a series of sine

terms whose frequencies are integer multiples of the

repetition frequency, f

where ω

= 21πf

, fr = 1/T, and

. . . are the phases of

the harmonics.

The phase angles can be eliminated by resolving the terms into

in-phase and quadrature components.

The complete series can be written compactly as the

summation of n terms for which n has values of 1, 2, 3 . . .

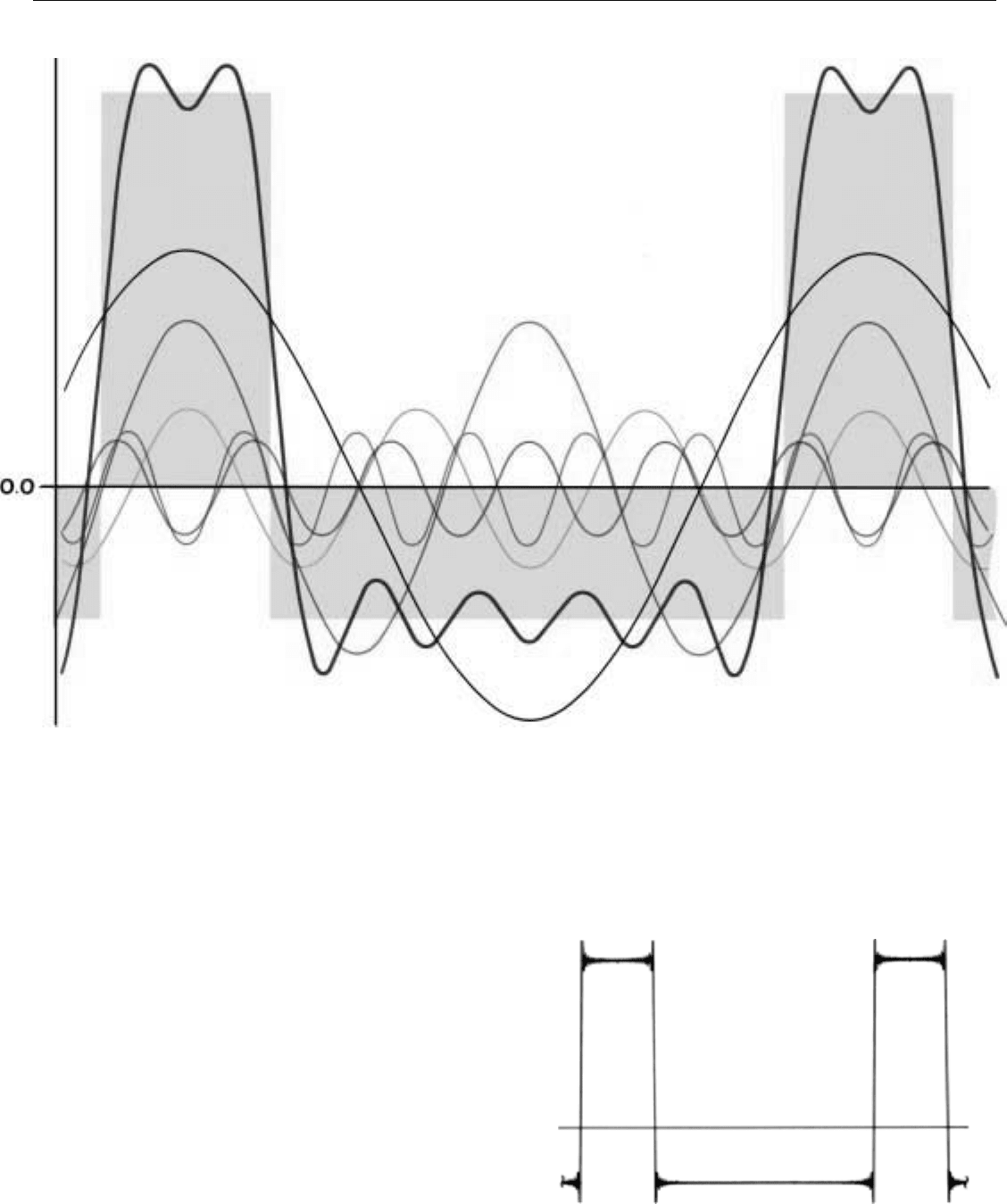
And a still more rectangular wave has been produced in

Fig. 13 (above) by adding only four harmonics.

The more harmonics included, the more rectangular the

wave will be and the less pronounced the ripple.

In Fig. 14, the ripple has been reduced to negligible pro-

portions—except at the sharp corners—by including 100

harmonics.

If the corners were rounded, as they commonly are in

practice—e.g. the shape of a radar’s transmitted pulses and

the shape of the received echoes or the shape of the pulses

in a digital computer—even this ripple would be negligible.

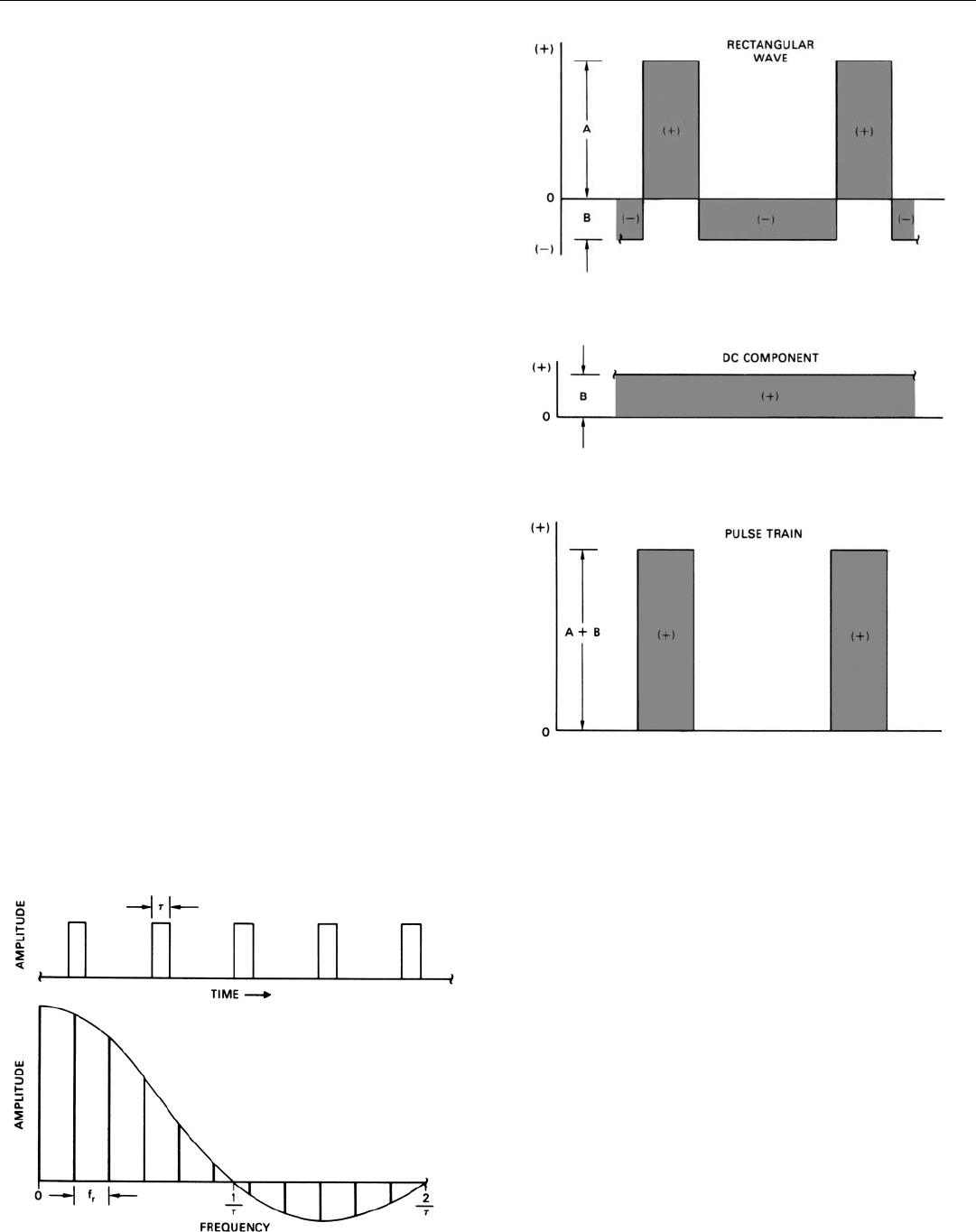
To create a train of pulses—i.e., a waveform whose

amplitude alternates between zero and, say, one—with a

series of sine waves, a zero-frequency, or dc, component

must be added.

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

215

13. Rectangular wave produced by adding four harmonics to the fundamental. Shape of composite wave is determined by relative amplitudes

and phases of harmonics. For shape to be rectangular, all harmonics must go through a positive or negative maximum at the same time as

the fundamental.

14. Rectangular waveshape produced by combining 100 har-

monics. Note reduction in ripple.

PART IV Pulse Doppler Radar

216

Its value equals the amplitude of the negative loops of

the rectangular wave, with sign reversed (Fig. 15, above).

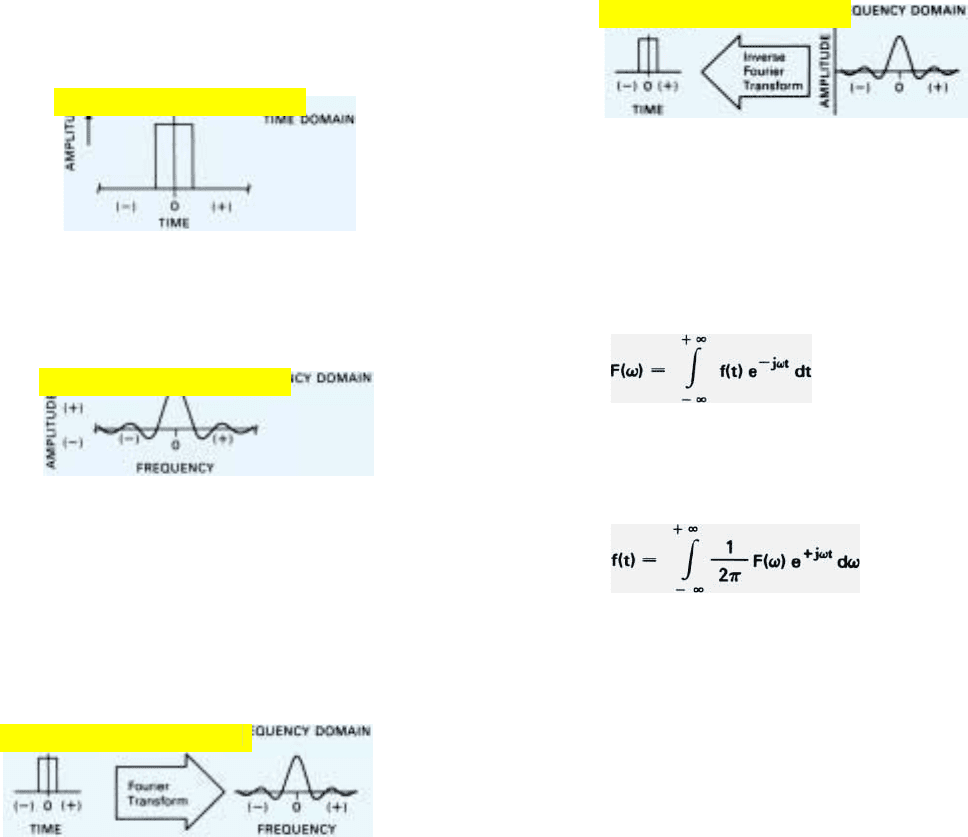
Spectrum of a Train of Pulses. A portion of an infinitely

long train of rectangular pulses is plotted in Fig. 16.

Beneath it is a plot of amplitude versus frequency for the

individual waves which would have to be added together to

produce the waveform—the wave’s spectrum. The equation

relating the spectrum to the waveform is called the Fourier

transform—see panel on facing page.

Each line of this spectrum, except the zero-frequency

line, represents a sine wave which goes through a maxi-

mum at the same time as the fundamental. The phases of

the waves are thus implicit in the plot. In alternate lobes of

the envelope, the phase of the harmonics is shifted by

180°, a fact indicated by plotting the amplitudes of these

harmonics as negative.

15. To produce a train of rectangular pulses from a rectangular wave,

a dc component must be added.

16. Portion of an infinitely long rectangular pulse train and the

spectrum of the train.

Since all of the waves are integer multiples of the funda-

mental, the frequency of which is f

, the spacing between

lines is f

The first null in the envelope within which the lines fit

occurs at a frequency equal to one divided by the

pulsewidth, 1/τ. Subsequent nulls occur at multiples of

1/τ.

Spectrum of a Pulse Modulated Radio Wave. As

explained in Chap. 5, when the amplitude of a carrier

wave of frequency f

is modulated by a single sine wave of

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

217

THE FOURIER TRANSFORM

Time and Frequency Domains. A graph {or equation) relating the

amplitude of a signal to time represents the signal in what is called

the

time domain

A graph (or equation) relating the amplitude and phase of the signal

to frequency (the signal’s spectrum) represents the signal in what is

called the

frequency domain

A signal can be represented completely in either domain.

Consequently, what one does to the signal shows up in both

representations.

Switching Between Domains. The representation of a signal in

one domain can readily be transformed into the equivalent

representation in the other domain.

The mathematical expression for transforming from the time domain

to the frequency domain is called the

Fourier transform

The mathematical expression for transforming from the frequency

domain to the time domain is called the

inverse Fourier transform

Together, the two transforms are called a

transform pair

Deriving the Transforms. To derive the Fourier transform, you write

an expression for the signal as a function of time, substitute it for f(t)

in the following equation

and perform the indicated integration.

Similarly, to derive the inverse transform, you write an expression

for the signal as a function of ω, substitute it for F(ω) in this next equa-

tion

and perform the indicated integration. The variable ω is frequency in

radians per second (ω = 2π f), and e

—jωt

is the exponential form of

the expression, cos ωt – j sin ωt.

Value of the Concept. The concept of the two domains and transfor-

mation between them is immensely useful. In radar work, in fact, it is

indispensable. The crux of modern signal processing design is trans-

lating from one representation to the other. Range resolution and

range measurement (except for chirp) may be readily perceived only

in the time domain. Doppler resolution, doppler range-rate measure-

ment, and certain aspects of high resolution ground mapping, on the

other hand, may be readily perceived only in the frequency domain.

Click for high-quality image

PART IV Pulse Doppler Radar

218

frequency f

, two sidebands are produced—one f

above

, the other f

below f

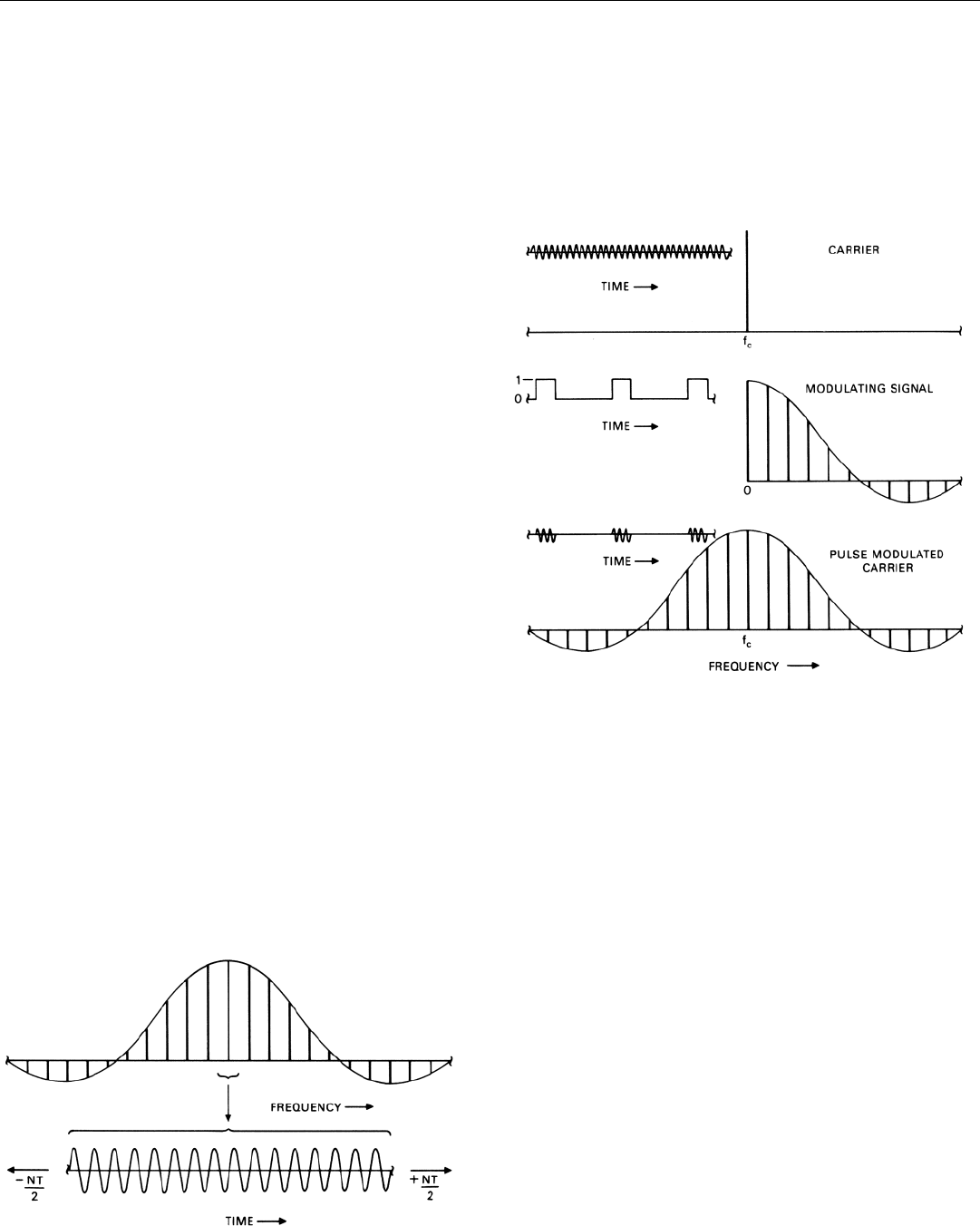
Therefore, when the carrier of a coherent transmitter is

modulated by a pulsed video signal, such as that illustrated

in Fig. 17 (below), the sine wave represented by each line

in the spectrum of the modulating signal produces two

sidebands.

17. When a continuous carrier wave is modulated by an infinitely

long pulsed video signal, each harmonic of the video signal pro-

duces a sideband above and below the carrier frequency.

18. Each line in the spectrum of a pulse modulated carrier repre-

sents a single sine wave the length of the pulse train.

The fundamental produces sidebands f

hertz above and

below the carrier. The second harmonic produces sidebands

above and below the carrier, and so on. The zero fre-

quency line, of course, produces an output at the carrier

frequency.

The spectrum of the envelope is thus mirrored above and

below the carrier frequency. The resulting radio frequency

spectrum is exactly the same as the spectrum we obtained

for a continuous train of coherent pulses in Experiment 3 of

the preceding chapter.

What the Spectral Lines Represent. One aspect of the

spectrum of a pulsed carrier wave which some people have

difficulty seeing is that each of the individual spectral lines

represents a continuous wave. That is, a wave of constant

amplitude and constant frequency, which continues unin-

terruptedly in time from the beginning to the end of the

pulse train (Fig. 18). How can that be, when the transmitter

is “on” for only a fraction of each interpulse period?

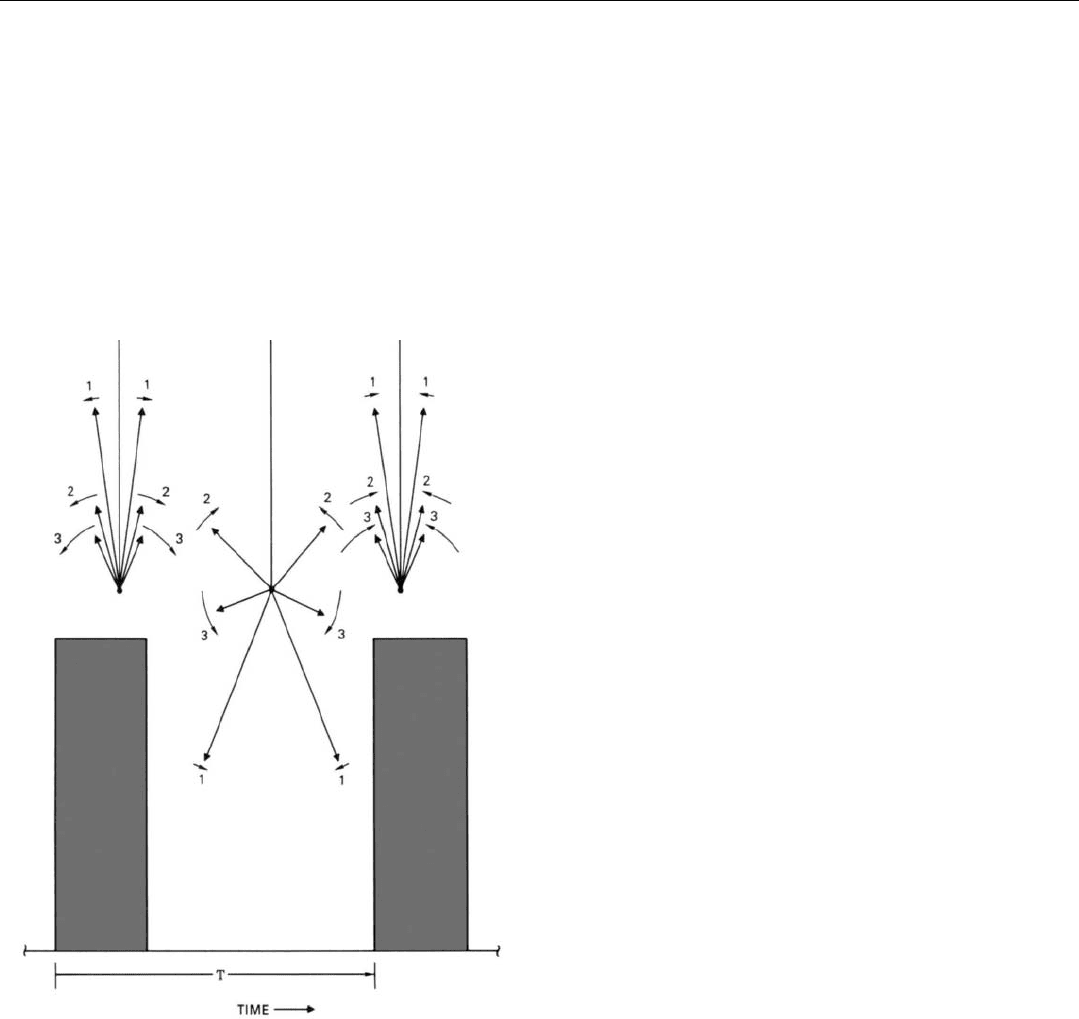
Briefly, the explanation is this. The amplitudes and

phases of the fundamental and its harmonics are such that

they completely cancel the carrier, as well as each other,

during the periods between pulses. Yet they combine to

produce a signal having the carrier’s wavelength and the

full power of the transmitter, during the brief period of

each pulse.

This was illustrated for a rectangular wave in Fig. 14

and is illustrated in a cursory way for a pulsed radio wave

by the phasor diagrams of Fig. 19.

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

219

19. Phasors representing carrier (c) and first several sidebands of an

infinitely long pulse train. During the pulses, they combine con-

structively. Between pulses, they cancel.

They show how the carrier and the first three sidebands

above and below the carrier combine to produce the trans-

mitted pulses. The phasor representing the carrier is syn-

chronized with the strobe that provides the phase reference

for the phasors (see Chap. 5).

Therefore, the phasors representing the upper sidebands

rotate counterclockwise and the phasors representing the

lower sidebands rotate clockwise. The higher the order of

the individual sidebands, the more rapidly the phasors

rotate.

PART IV Pulse Doppler Radar

220

Since the harmonics are all integer multiples of the fun-

damental frequency and it equals the pulse repetition fre-

quency, once every repetition period, all of the phasors line

up. At this point, the phasors add constuctively.

There-

after, the counter-rotating phasors rapidly fan out. Pointing

essentially in opposite directions, they cancel the carrier

and each other for the balance of the period, only to come

together once again at the beginning of the next period.

That the waves represented by the phasors are continu-

ous is borne out by the fact that when a pulsed signal is

applied to a narrowband analog filter tuned to the frequen-

cy of one of the spectral lines, the filter’s output is a contin-

uous signal.

A pulsed signal has a true line spectrum, though, only if

the signal is infinitely long. Otherwise, the spectral lines

have a finite width. And how does the Fourier series tell us

what the width is? This question can be answered most

simply in terms of the spectrum of a single pulse. So let us

first see what the Fourier series tells us about that.

Spectrum of a Single Pulse. Strictly speaking, the

Fourier series applies to a signal only if the signal has a

repetitive waveform that can be assumed to continue unin-

terruptedly from the beginning to the end of time. In some

cases, though, we can safely make this assumption, even

though the waveform may not be repetitive at all.

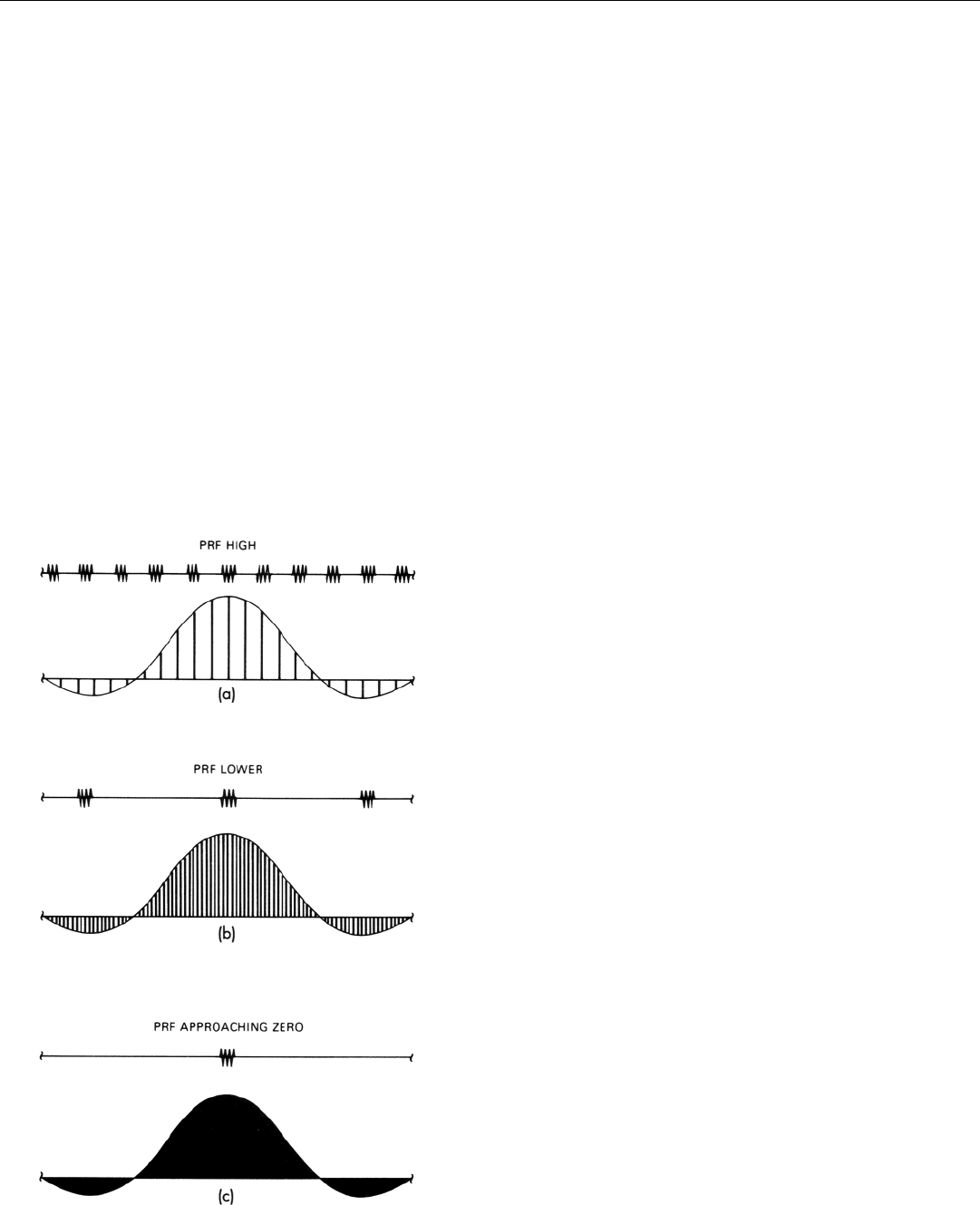
This is true in the case of a single rectangular pulse. We

start with a continuously repetitive form of the pulse

(Fig. 20a).

Keeping the pulse width constant, we gradually decrease

the repetition frequency. As we do so, the lines of the

pulsed signal’s spectrum move closer and closer together

(Fig. 20b). The envelope within which they fit, however,

retains its original shape, since that is determined solely by

the pulse width.

If we continue this process, stretching the time between

pulses to weeks, to years, to eons, to an infinite number of

eons, the separation between spectral lines ultimately dis-

appears.

We end up with a single pulse and a continuous spec-

trum that has exactly the same shape as the envelope of the

line spectrum of the continuously repetitive waveform

(Fig. 20c). This, you may recall, is what we found the

spectrum of a single pulse to be in Experiment 2 of the last

chapter.

Incidentally, if we pursue the above logic a step further,

we are led to an interesting conclusion. Since the pulse

train of which this single pulse is actually a part is infinitely

long, every point in the pulse’s spectrum represents a con-

20. Continuous pulse train of infinite length and its spectrum. As

PRF is reduced, spectral lines move closer together. As PRF

approaches zero, spectrum becomes continuous.

(a)

(b)

(c)

4. Except the phasors repre-

senting harmonics in the odd

numbered sidelobes, not

shown in the figure. They are

180° out of phase with the

others.

tinuous wave of infinite duration. How can that be?

Of course, no wave we shall ever see will have extended

to the end of time—and a lucky thing too. However, the

spectra of the signals we are considering here are exactly

the same as if the signals were comprised of infinitely long

waves.

So, in modeling spectral characteristics, it matters little

whether such long waves actually exist. With that point set-

tled, let us return to the question of what the Fourier series

tells us about spectral line width.

Line Width. Knowing the spectrum of a single pulse, we

can easily find the spectrum of a pulse train of limited

length, such as a radar would receive from a target.

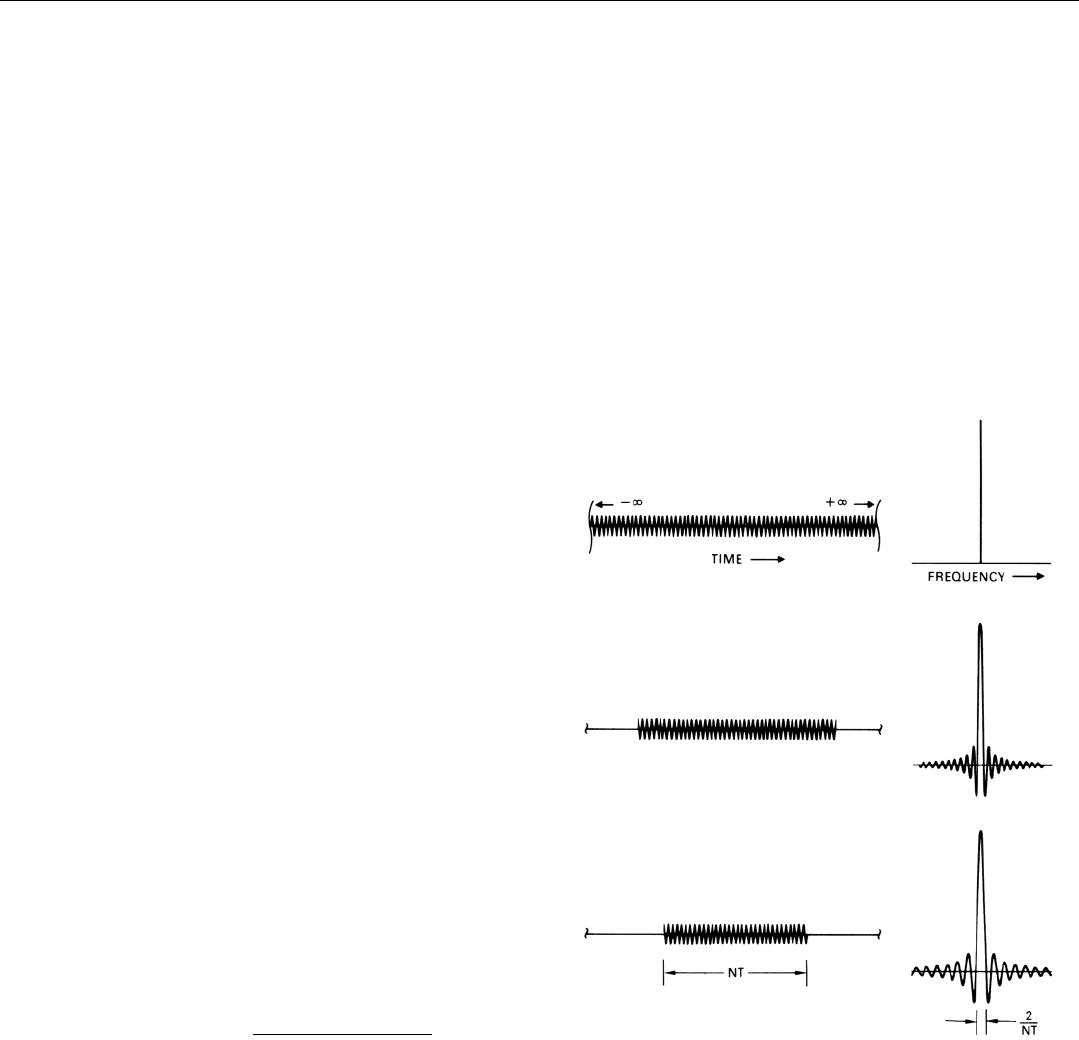
Suppose we wish to find the spectrum of a train of N puls-

es, having an interpulse period T, hence a total length NT.

We start by imagining an infinitely long pulse train. Each

line of the spectrum of this train, remember, represents a

continuous wave having a single frequency and an infinite

duration—a true CW signal. Holding the PRF and pulse

width constant, we gradually reduce the length of the train

(Fig. 21).

Since the constituent CW signals are the same length as

the train, each of them now becomes a single long pulse. As

the length of this pulse decreases, the spectral line repre-

senting it gradually broadens into a sin x/x shape. When we

finally reach the length, NT, of the pulse train in question,

the null-to-null width of the central lobe of this “line”

equals 2/(NT).

Thus, the Fourier series indirectly tells us that the spec-

trum of a pulse train of limited length differs from the spec-

trum of a train of infinite length only in that each spectral

line has a sin x/x shape. The null-to-null width of the line is

inversely proportional to the length of the pulse train.

Line width =

Length of pulse train

That, you’ll recall, is exactly what we found the line width to

be in Experiments 4 and 5 of the preceding chapter.

Some people find the foregoing explanation a bit unsatis-

fying. Somehow, it makes them a little uneasy to assume—

even though only for the sake of illustration—that, when

you key a transmitter “on” for a millionth of a second, you

are in effect transmitting myriad radio waves, waves that

began ages ago and will continue for ages to come, waves

that cancel one another completely throughout all of this

vast time, except for the glorious fraction of a second when

the transmitter is actually “on.”

CHAPTER 17 Mysteries of the Pulsed Spectrum Unveiled

221

21. CW wave represented by a single line in the spectrum of an

infinitely long pulse train. As the length of train is reduced,

this wave becomes a single pulse and its spectrum broadens

into a sin x/x shape.

PART IV Pulse Doppler Radar

222

If you are like these people, you may find it is helpful to

consider the spectrum of a pulsed signal from the point of

view of a lossless narrowband filter.

Spectrum Explained from a Filter’s Point of View

As was explained on page 212, a lossless narrowband fil-

ter integrates the energy of a signal (wave) in such a way

that the filter’s output builds up to a large amplitude only if

the frequency of the signal is the same as that to which the

filter is tuned.

In essence, the filter determines how close the frequen-

cies are to being the same by sensing the shift, if any, in the

phases of successive cycles of the input signal, relative to a

signal whose frequency is that of the filter.

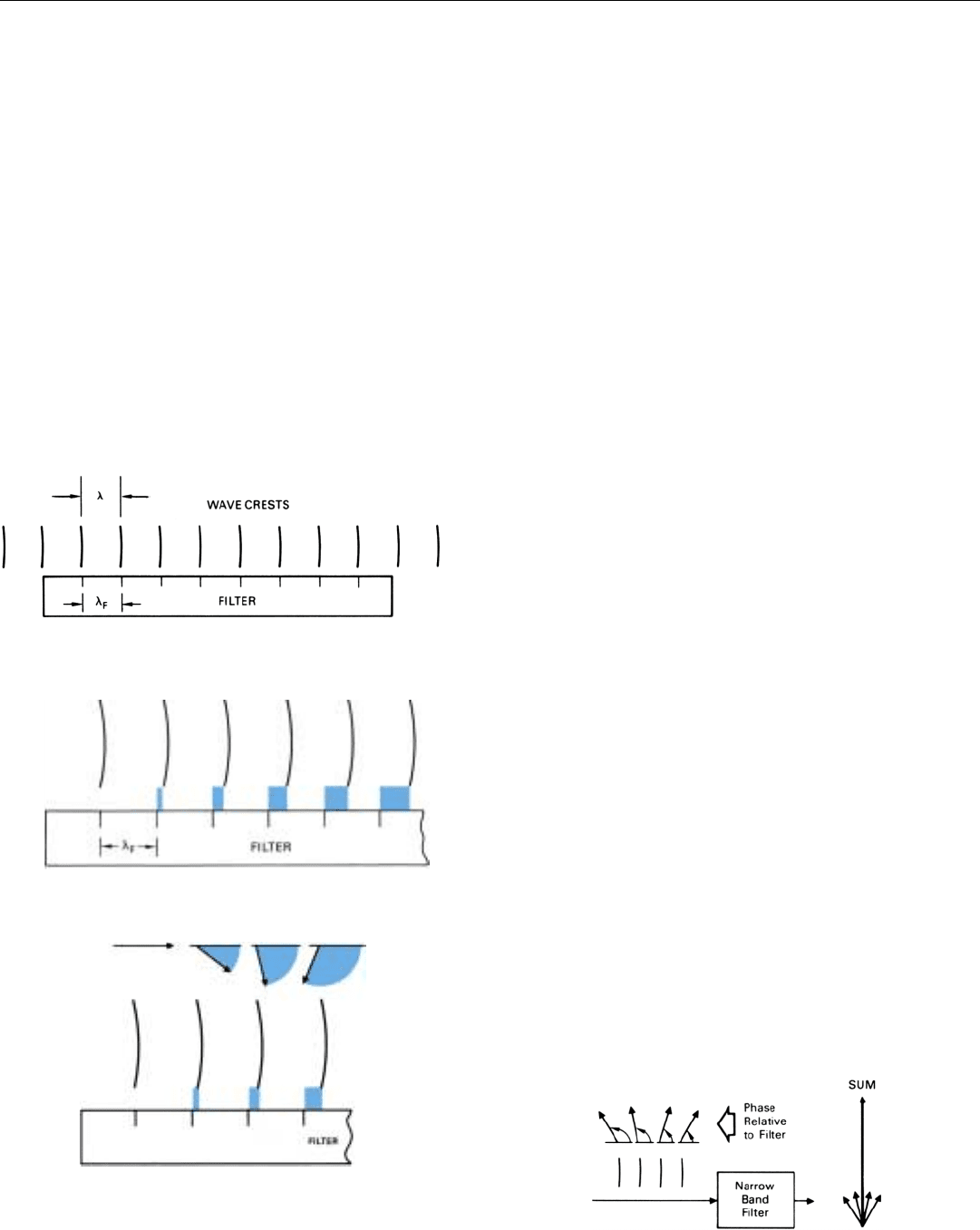
Analogy of a Filter to a Ruler. If the wave crests of the

input signal are represented graphically by a series of verti-

cal lines spaced at intervals equal to a wavelength, the filter

can be thought of as measuring the spacing between wave

crests with an imaginary ruler. On this ruler, marks are

inscribed at intervals of one wavelength for the frequency

to which the filter is tuned.

Quite obviously, if the filter is tuned to the exact fre-

quency of the wave, when the first mark is lined up with a

wave crest, all subsequent marks will similarly line up

(Fig. 22).

If the filter is tuned to a slightly different frequency, how-

ever, the first mark beyond the initial one will be displaced

slightly from the next wave crest; the second mark will be

displaced twice as much from the following wave crest; the

third mark, three time as much, and so on (Fig. 23). The

displacements correspond to the phases of the individual

cycles of the signal as seen by the filter; the progressive

increase in displacement corresponds to the progressive

shift in phase from once cycle to the next.

Now, the amplitude of each cycle of the wave, as well as

the phase of that cycle relative to the corresponding mark

on the ruler, can be represented by a phasor (Fig. 24).

What the narrowband filter does is add up—integrate—the

phasors for successive cycles (Fig 25). If n phasors point in

22. A lossless narrowband filter can be thought of as measuring

the spacing of a signal’s wave crests with an imaginary ruler.

23.

If the filter’s frequency is higher than the signal’s, the phase shift

between the wave crests and the marks on the ruler builds up.

24. The amplitude and phase of each cycle of the wave can be

represented by a phasor.

25. In essence, the filter adds up the phasors for successive cycles.