George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

Now, the role of the filter is to further narrow the receiv-

er passband by integrating the energy of successive pulses.

What the filter does, in effect, is add up the phasors. In the

case of noise, because of the randomness of phase, the puls-

es largely cancel.

At the end of the integration period, the magnitude of the

sum—the integrated noise, N

→

—is little different than the

amplitude of a single noise pulse and only a fraction of the

sum of the amplitudes of the individual pulses. The integra-

tion period, we will assume, corresponds to a single time-

on-target.

Noise Alone, Successive Times-on-Target. We repeat the

experiment a great many times—each repetition corre-

sponding to a separate time-on-target. As expected, because

of the randomness of the noise, the magnitude and phase of

the energy that accumulates in the filter, N

→

, vary widely

from one time-on-target to the next.

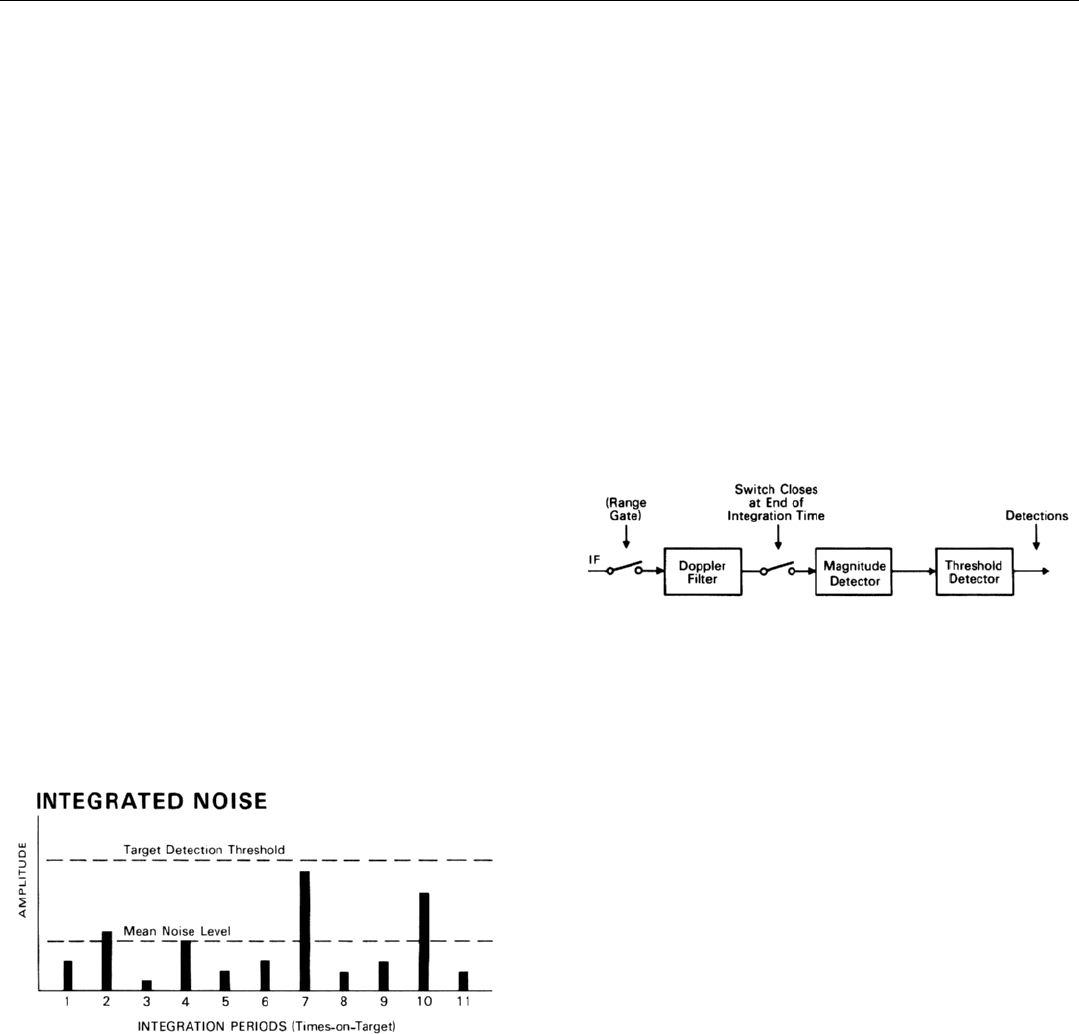
At the end of each time-on-target, the magnitude of the

accumulated energy is “detected” (Fig. 30). That is, a voltage

(video signal) proportional to the magnitude is produced.

Incidentally, since the integration takes place before this

detection, the integration is called predetection integration.

The video outputs for successive times-on-target are

plotted in Fig. 31.

CHAPTER 10 Detection Range

129

30. At the end of each integration period (time-on-target), the

amplitude of the energy accumulated in the filter is detected

and applied to a threshold detector.

31. Outputs of the amplitude detector of Fig. 30 at end of successive

times-on-target.

4. Actually, the phase of a tar-

get’s returns varies from pulse

to pulse in proportion to the

target‘s doppler frequency.

But as seen by a filter tuned to

this frequency, the phase is

constant.

As you can see, over a number of integrated periods, the

magnitude of the integrated noise varies randomly about a

mean value. Though not illustrated here, the variation in

phase is equally random.

Target Signal Only. We repeat the experiment; this time,

with the target present but (through some magic) with the

noise absent. Now each time the range gate is closed, the fil-

ter receives a pulse of energy from the target. Unlike the

noise pulses, these all have the same phase.

When integrat-

5. During the very short time

interval discussed here.

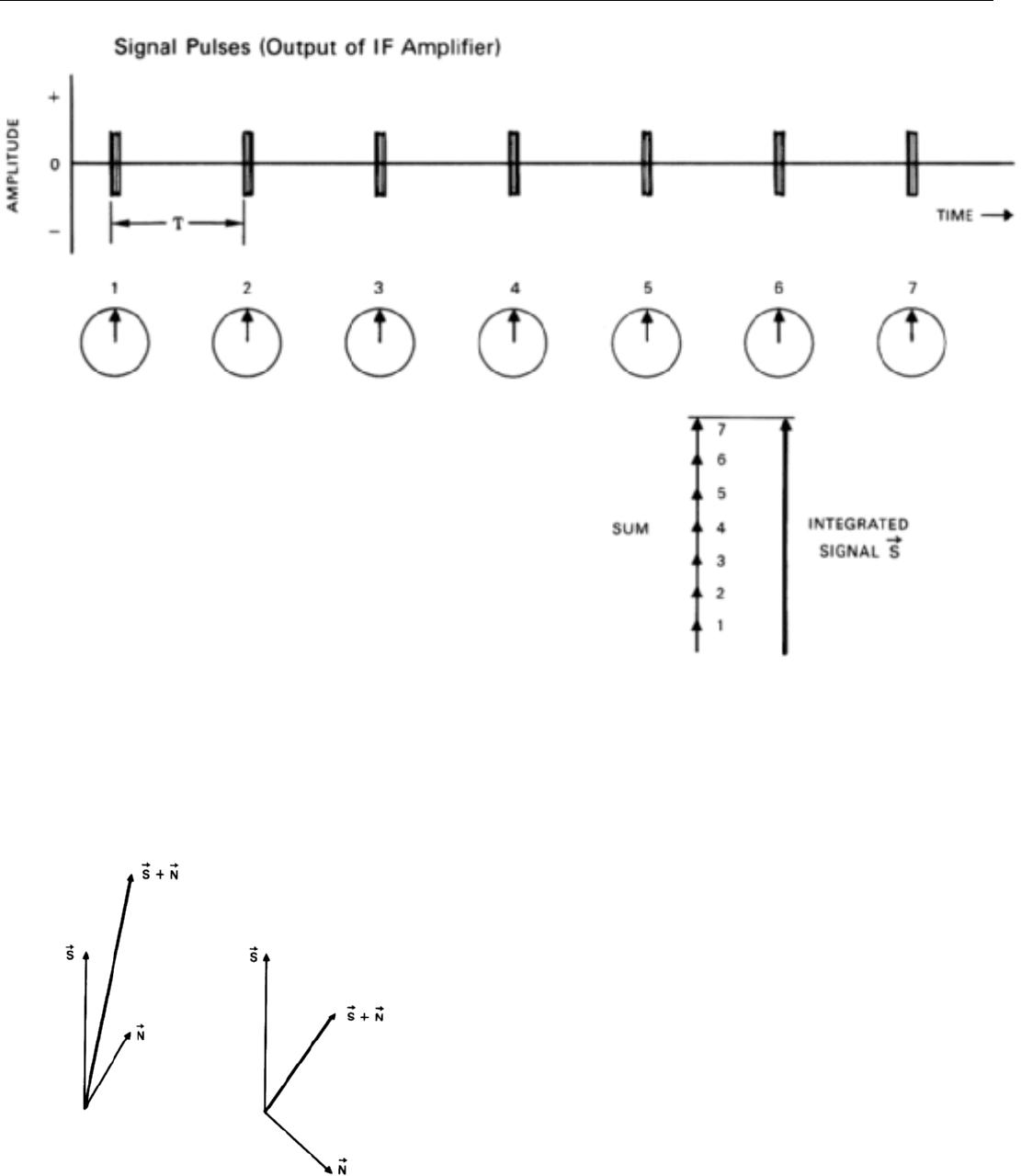
PART III Radar Fundamentals

130

ed by the filter, they add constructively. At the end of each

integration period, their sum (Fig. 32, above)—the magni-

tude of the integrated signal, S

→

—very nearly equals the

sum of the amplitudes of the individual pulses.

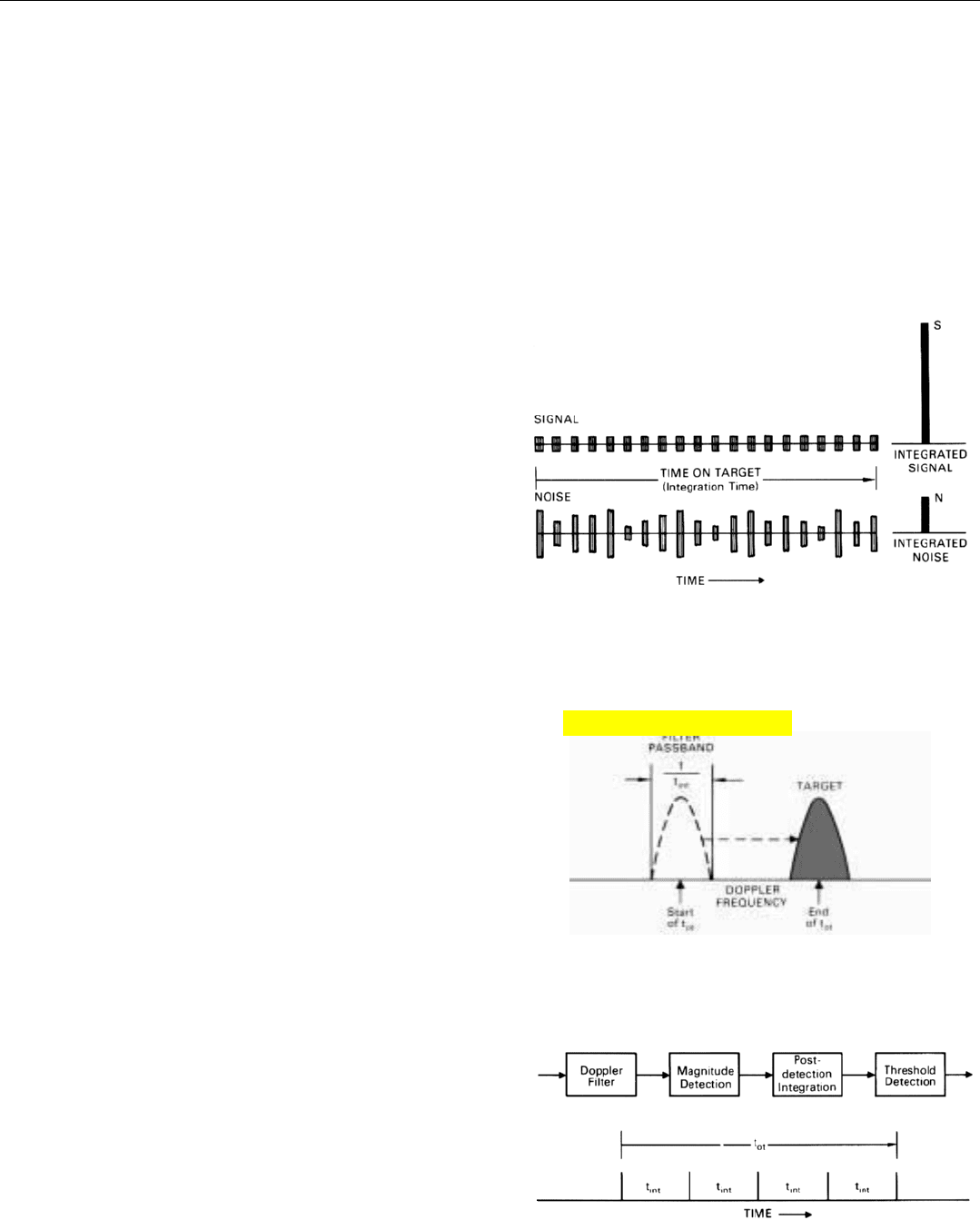
How Signal and Noise Combine. Finally, we repeat the

experiment several times with both target signal and noise

present. Although they are indistinguishably mixed and so

integrate simultaneously, we can visualize the result more

clearly if we think of the signal and noise as being integrat-

ed separately and of their sums, S

→

and N

→

, being vectorially

added together at the end of the time-on-target. The magni-

tude of the vector sum, of course, depends not only upon

the magnitudes of S

→

and N

→

, but upon the phase angle

between them (Fig. 33). If the noise is in phase with the

signal, the two vectors will combine constructively; if the

noise is 180˚ out of phase, they will combine destructively;

and there are myriad possible combinations in between.

For any one time-on-target, therefore, the magnitude of the

energy that accumulates in the filter equals the magnitude

32. Phasor representation of signal pulses applied to doppler filter. Because phase is same from pulse to pulse, integrated signal is many times

amplitude of individual pulses.

33. Amplitude of integrated signal plus noise varies widely,

depending on amplitudes and phases of

→

and

→

of the integrated signal, S

→

, plus or minus some fraction of

the magnitude of the integrated noise, N

→

Improvement in Signal-to-Noise Ratio. How predetec-

tion integration improves the signal-to-noise ratio should

now be fairly clear. Whereas the noise energy that accumu-

lates in the filter may vary widely from one integration peri-

od to another, the mean level of the noise energy is essen-

tially independent of the integration time. The integrated

signal energy (target return), on the other hand, increases in

direct proportion to the integration time. By increasing the

integration time, therefore, the signal-to-noise ratio can be

increased significantly.

An individual target echo, for example, may contain only

one thousandth as much energy as an individual noise

pulse, yet after ten thousand pulses have been integrated,

the signal may be considerably greater than the noise.

Indeed, the improvement in signal-to-noise ratio achiev-

able through predetection integration is limited only by (1)

length of the time-on-target, t

, or (2) the maximum practi-

cal length of the integration time, t

int

, if that is less than t

or (3) the length of time over which the target’s doppler fre-

quency remains close enough to the same value for the tar-

get echoes to be correlated by the filter (Fig. 34). The

greater the improvement in signal-to-noise ratio, of course,

the weaker the target echoes can be and still be detected;

hence, the greater the detection range.

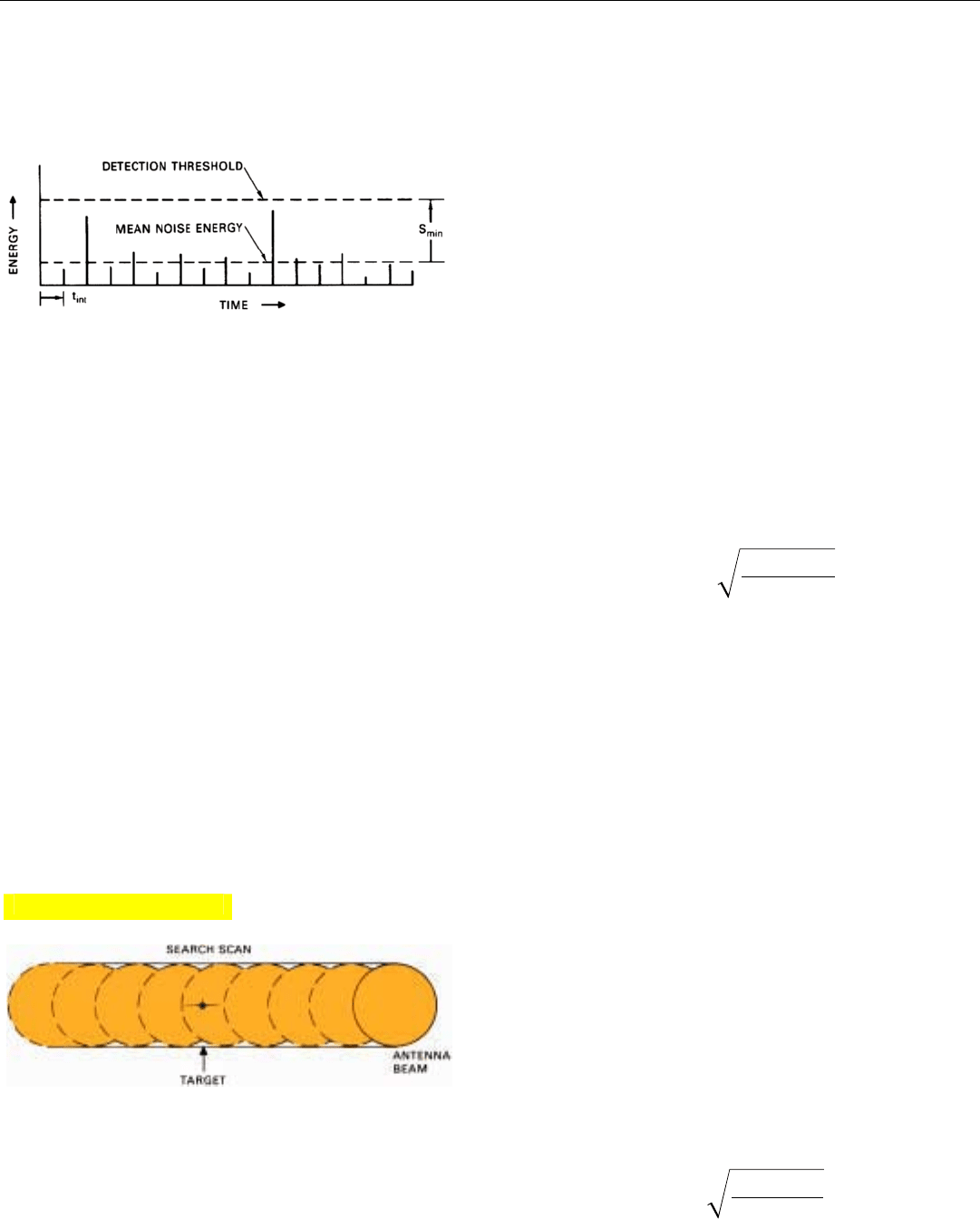
Postdetection Integration

Sometimes, the maximum practical integration time is a

good deal less than the time-on-target. Take, for example, a

situation where the doppler frequencies of expected targets

may be subject to rapid change. Since the width of the filter

passband is inversely proportional to the integration time

(bandwidth ≅ 1/t

int

), making t

int

as long as t

could narrow

the passband to the point where the signal may very well

move out of it long before the time-on-target ends (Fig. 35).

In such instances, rather than lose any of the signal, the

integration time of the doppler filter is made short enough

to provide the required bandwidth, and integration and

video detection are repeated throughout the time-on-target

(Fig. 36). The video outputs for successive integration peri-

ods are then added together (integrated) and their sum is

applied to the threshold detector. This second integration

process is fundamentally the same as that employed in non-

doppler radars. Since it takes place after video detection, it

is called postdetection integration, or PDI.

Once the output of a doppler filter (or the output of the

IF amplifier in a non-doppler radar) has been converted to

CHAPTER 10 Detection Range

131

34. The improvement in signal-to-noise ratio is ultimately limited

only by the time-on-target, provided target echoes remain

correlated.

35. Situation in which target’s doppler frequency changes radi-

cally during time-on-target, t

. If filter integration time, t

int

, is

made equal to t

, target will move out of passband before

integration is finished.

36. Problem is solved by dividing t

into a number of integration

periods short enough to provide adequate doppler bandwidth

and adding up filter outputs for entire time-on-target.

Click for high-quality image

PART III Radar Fundamentals

132

a video signal of single polarity, noise will no longer cancel

when integrated. Rather, it will build up throughout the

integration time in exactly the same way as the signal.

Consequently, with PDI the mean signal-to-noise ratio can-

not be increased. Nevertheless, an equivalent improvement

in detection sensitivity may be achieved. To see why, we

must look a little more closely at PDI.

Actually, PDI is nothing more than averaging. It has the

same effect as passing the video signal through a low-pass

(as opposed to bandpass) filter. You can visualize this most

clearly by thinking of the video signal as consisting of a

constant (dc) component, the amplitude of which corre-

sponds to the mean level of the signal, plus a fluctuating

(ac) component.

The amplitude of the dc component is unaltered by the

averaging, but the amplitude of the ac component is

reduced. The higher the frequency of the fluctuation and

the greater the integration time (i.e., the larger the number

of inputs averaged), the greater the reduction will be.

Averaging improves detection sensitivity in two important

ways.

First, it reduces the average deviation of the integrated

noise energy. Consequently, without increasing the false-

alarm probability, the target-detection threshold can be set

closer to the mean noise level (Fig. 37). The integrated sig-

nal need not be as great to cross the threshold, and the

weaker echoes of more distant targets can be detected.

The second improvement averaging makes is more sub-

tle. As we just saw, when target return is received, the inte-

grated signal is vectorially added to the integrated noise.

Because of the randomness of the noise, as often as not, the

noise will be out of phase with the signal and so will com-

bine with the signal destructively.

However, when the integrated signal plus noise is aver-

aged over many integration periods, the fluctuations due to

the noise tend to cancel out, leaving only the signal. The

possibility of missing an otherwise detectable target because

of the destructive combination of it with noise is thus great-

ly reduced.

Together, these two effects of PDI can substantially

reduce the signal-to-noise ratio required for detection. As

illustrated in Fig. 38, the fluctuations in the noise and in

the signal-plus-noise can, in the extreme, be reduced to the

point where a signal can be detected when the mean signal-

to-noise ratio is substantially less than one.

Sometimes, the equivalent of postdetection integration is

approximated by using a so-called “m out of n” detection

37. By averaging the noise outputs of a doppler filter during the

time-on-target, PDI enables the target-detection threshold to be

set much lower, without increasing the false-alarm probability.

38. The two effects of PDI allow a signal to be detected even when

the mean signal-to-noise ratio is less than one.

Click for high-quality image

criteria. If the time-on-target spans n predetection integra-

tion periods, rather than requiring only one threshold

crossing per time-on-target as a condition for detection, the

signal processor requires m crossings (Fig. 39).

The chance of isolated noise spikes producing false

alarms is thereby reduced. The detection threshold can be

lowered without increasing the false-alarm probability, and

more distant targets can be detected.

Summary

Since radio waves of the frequencies used by airborne

radars travel essentially in straight lines, a target must be

within the line of sight to be detected. Range may be fur-

ther limited by clutter or man-made interference. Ulti-

mately, it is determined by the signal-to-noise energy ratio.

The principal source of noise is thermal agitation in the

input stages of the receiver. The noise energy is commonly

expressed in terms of a figure of merit, F

, relating it to an

approximation of the external noise, provided by thermal

agitation in a resistor connected across the receiver’s input

terminals. In the case of low-noise receivers, external noise

sources become more significant, and noise is expressed in

terms of an equivalent “system” noise temperature.

How much energy is received from a target depends pri-

marily upon (1) the radar’s average transmitted power,

antenna gain, and effective antenna area; (2) the time-on-

target; (3) the target’s range, R, and radar cross section, σ—

a factor which accounts for the size, reflectivity, and direc-

tivity of the target.

Most radars integrate the return received as the antenna

scans across a target. If performed before video detection

(predetection integration), the integration increases the sig-

nal-to-noise ratio in direct proportion to integration time. If

performed after video detection (PDI), the integration

accomplishes two things: (1) averages out the fluctuations

in the noise, thereby reducing its peaks, and (2) averages

out the destructive combination of the noise with the sig-

nal, thereby reducing the possibility of missing an other-

wise detectable target.

For a target to be detected, the integrated signal must

exceed a threshold set high enough to keep the probability

of noise crossings acceptably low. In doppler radars, to

maintain a constant, optimum false alarm rate (CFAR), the

threshold setting of the magnitude detector for each

doppler filter’s output is based on the mean noise level in

the outputs of an ensemble of adjacent filters, as well as on

measurement of the mean noise level in the outputs of all

the filters.

CHAPTER 10 Detection Range

133

• Mean noise power = F

k T

B or k T

B watts

= Receiver noise figure

= Noise temperature (nominally 290° K)

k = Boltzmann’s constant

= 1.38 x 10

-23

watt-second / °K

B = Receiver bandwidth (hertz)

= System noise temperature (including

internal + external noise)

• Mean noise energy = kT

B t

= duration of the noise

• Mean noise energy =

(Matched filter)

• Mean noise energy = kT

(Doppler radar)

• Signal energy =

(4π)

avg

= Average transmitted power, watts

G = Antenna gain

σ = Radar cross section of target

= Effective area of antenna

= Time on target

R = Range

k T

avg

G σ A

Some Relationships To Keep In Mind

39. Sometimes the equivalent of PDI is obtained by requiring m

out of n threshold crossing in a time-on-target for a detection.

Here m = 2 and n = 8.

135

The Range Equation,

What It Does and

Doesn’t Tell Us

n the last chapter, we learned that within the line of

sight, in the absence of interference and competing

ground return, detection range is ultimately deter-

mined by the ratio of the energy received from a tar-

get—the signal—to the energy of the background noise.

We identified the principal factors which determine the

signal and noise energies and became acquainted with the

detection process.

Building on that knowledge, in this chapter we will

write a general equation for maximum detection range and

analyze it to see how the individual factors we have identi-

fied influence the range. We will then narrow down to the

special case of volume search. Finally, we will consider the

statistical variation in detection range and see how it is

accounted for.

General Range Equation

As we saw in the preceding chapter, when the radar

antenna is trained on a target (Fig. 1), the energy received

from the target during any one integration time is roughly

Received signal energy ≅

avg

G␴A

int

(4␲)

where

avg

= average transmitted power

G = antenna gain

σ = radar cross section of target

= effective antenna area

int

= integration time

R = range

1. Factors determining the received signal energy.

Click for high-quality image

For the target to be detected, this energy plus the accom-

panying noise energy must exceed a certain threshold

value. It is set just high enough above the mean noise level

to reduce the probability of noise peaks crossing the thresh-

old—false alarms—to an acceptably low value.

On average, the minimum energy that a signal must have

to cross the detection threshold is the difference between

the detection threshold and the mean level of the noise.

This difference (Fig. 2) is commonly represented by the

term S

min

Minimum detectable signal energy = S

min

Assuming perfect integration, the maximum range at

which a given target will be detected is the range at which

the received signal energy becomes equal to S

min

. Setting

the expression for signal energy equal to S

min

and solving

for range, therefore, yields a simple equation for the maxi-

mum detection range.

max

≅

avg

G␴A

int

(4␲)

min

(Antenna trained on target)

As it stands, the equation applies only when the antenna is

continuously trained on the target and the target is in the

center of the mainlobe, i.e., when a target is being spotlight-

ed. (Bear in mind that though the antenna may be continu-

ously trained on the target, t

int

is limited to the period of

time that the phase of the target signal remains correlated.)

In search, the maximum integration time is limited to the

time the antenna takes to sweep across the target—the

time-on-target, t

. Moreover, the beam is actually centered

on the target only for an instant, if centered at all. We can

eliminate the first limitation simply by replacing t

int

with t

Temporarily, at least, we can get around the second limita-

tion by pretending that the antenna gain is the same over

the entire solid angle encompassed by the mainlobe and

that, for the particular scan being used, the target is cen-

tered in the beam’s path (Fig. 3).

Under these conditions, the equation gives the maxi-

mum detection range for a single search scan.

max

≅

avg

G␴A

(4␲)

min

(Single scan of antenna)

PART III Radar Fundamentals

136

2. Integrated noise energy at end of successive integration times,

int

. On average, for a target to be detected integrated signal

energy must equal S

min

3. Simple range equation can be applied to search by pretend-

ing that transmitted energy is uniformly distributed over cross

section of antenna beam and target is centered in beam’s

path.

Click for high-quality image

Incidentally, if we replace t

with the pulse width, τ, and

avg

with the peak power, P, the equation gives the range for

single-pulse detection.

max

≅

PG␴A

␶

(4␲)

min

(Single pulse: non-doppler radar)

Assuming that postdetection integration is accounted for

separately, this form of the equation applies to non-doppler

radars (Fig. 4).

Omissions. Regardless of which of these forms we use,

the equation is incomplete. Among the more obvious omis-

sions are

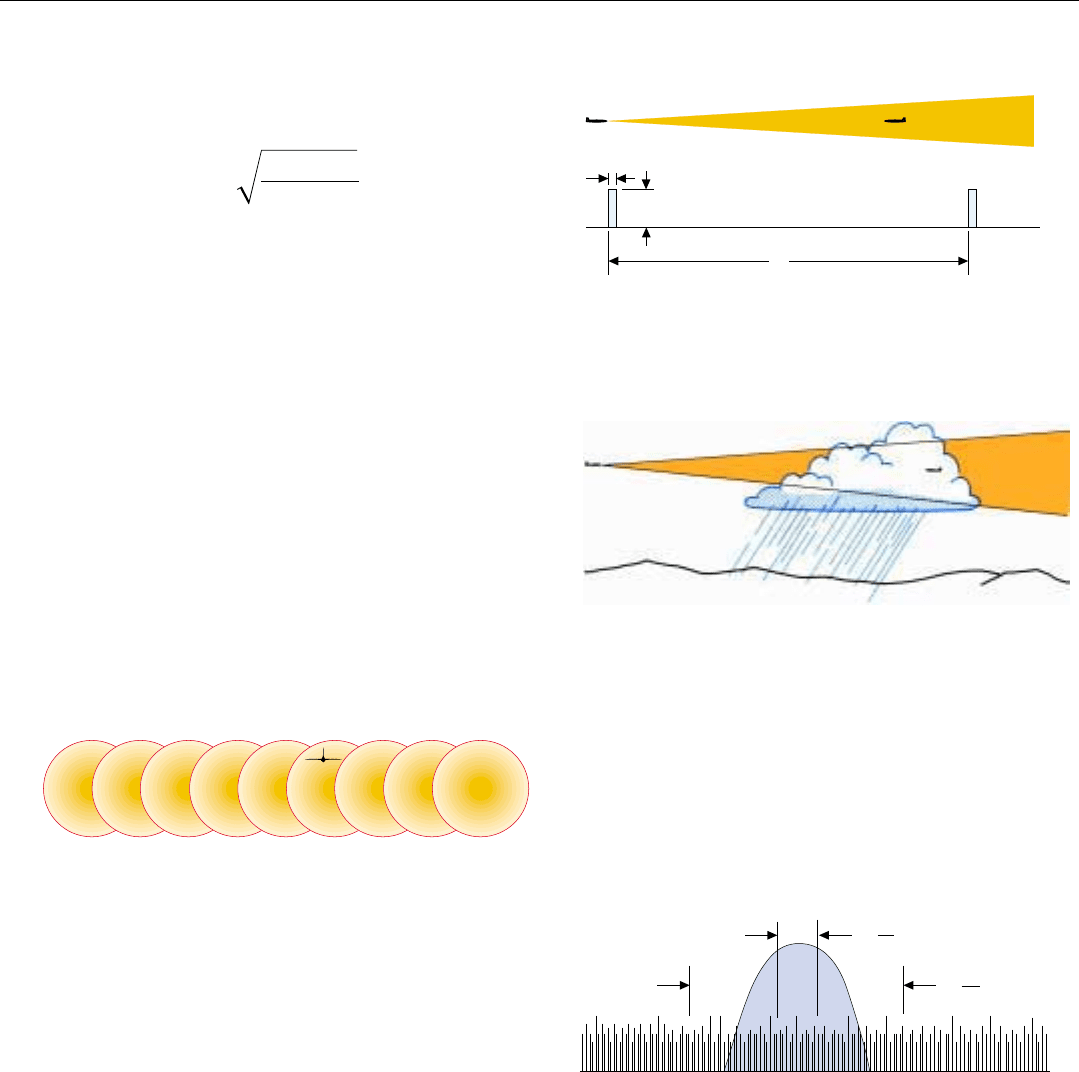
• Absorption and scattering in the atmosphere (Fig. 5)

• Reduction in signal energy due to the target not neces-

sarily being centered in the path of the scanning

antenna beam (this is called elevation beamshape loss)

• The further reduction in signal energy as the beam

sweeps across the target (Fig. 6) due to the fall-off in

two-way antenna gain at angles off beam center (this

is called azimuth beamshape loss)

• Losses due to imperfect IF-filter matching—some

noise being unnecessarily passed and/or some signal

energy being rejected (Fig. 7)

• Loss due to the target not necessarily being centered

in a doppler filter

• Degradation of signal-to-noise ratio due to imperfect

integration of the target return

• Effects of system degradation in the field

Nevertheless, the equation illustrates the relative contribu-

tions of what we have seen to be some of the more funda-

mental factors.

A More Revealing Form of the Equation. The contribu-

tion of a couple of the factors represented by terms in the

range equation can be seen more easily if we modify it

CHAPTER 11 The Range Equation: What It Does and Doesn’t Tell Us

137

4. Range equation can be applied to non-doppler radars by sub-

stituting pulse width, ␶, for t

int

and peak power P, for P

avg

Postdetection integration must be accounted for separately.

5. One of the many important losses not accounted for by the

simple range equation is atmospheric attenuation.

6. Other factors not directly accounted for include possibility of

target not being centered in beam’s path and fall off in two-

way gain of the antenna at angles off beam center.

1. All omitted factors which

reduce the signal-to-noise

ratio are accounted for by

including a loss factor, L, in

the denominator.

(a)

(b)

7. IF–filter mismatch: (a) some signal being rejected that is

stronger than accompanying noise; (b) some noise being

passed that is stronger than accompanying signal.

10. Decreasing system noise has the same effect on detection

range as increasing power by the same factor.

PART III Radar Fundamentals

138

9. Tripling transmitter power would increase detection range by

only 32 percent.

8. Since the detection threshold is related to mean noise level in

a complex way, detection range can be expressed in terms of

noise energy most simply by solving for the range at which the

integrated signal-to-noise ratio is one.

slightly. First, since S

min

is related in a fairly complex way to

the mean noise energy, kT

, if we back off from solving for

the maximum detection range and solve merely for the range

at which the integrated signal-to-noise ratio is one, we can

substitute kT

, directly for S

min

(Fig. 8). Second, since

antenna gain is proportional to effective antenna area divid-

ed by wavelength squared (G ∝ A

/λ

), we can consolidate

terms relating to the antenna by substituting A

/λ

for G.

With these changes, the equation for a single search scan

becomes

∝

avg

σt

␭

(Single search scan: SNR = 1)

where R

is the range at which the integrated signal-to-

noise ratio (SNR) is one, ␭ is the wavelength, and the other

terms are as previously defined.

What the Range Equation Tells Us

Incomplete as it is, the equation reveals a good deal not

only about the effect of changing various parameters, but

about some of the trade-offs which must be made in

designing a radar.

Average Power. The equation tells us, for example, that

increasing the power of the transmitter by a given factor

increases the detection range by only about the fourth root

of that factor. If we were to increase the power by, say, three

times (Fig. 9), the detection range would increase by only

about 30 percent (R

= R

公僒3 ≅ 1.32).

Noise. At the same time, the equation tells us that

decreasing the mean level of the background noise (kT

) by

a given factor has the same effect as increasing the average

power by the same factor. If we could reduce the noise by

50 percent, for example, the detection range would increase

by the same amount (Fig. 10) as if we had doubled the

power, which is about 20 percent (R

= R

公僒2 ≅ 1.19 R

CHAPTER 11 The Range Equation: What It Does and Doesn’t Tell Us

139

13. Doubling antenna diameter would double detection range,

provided scan was slowed to provide same time-on-target.

Time-on-Target. The equation also enables us to predict

the effect of changes in time-on-target, or integration time.

Suppose that by slowing down the scan, we were to double

the time-on-target. Provided the target return could still be

integrated, this would have the same effect as doubling the

power (Fig. 11).

Radar Cross Section. The equation further enables us to

predict the differences in the ranges at which a given radar

can detect targets of different sizes.

Suppose, for example, that the radar detects a target hav-

ing a certain radar cross section at a range of 40 miles.

Provided that the targets’ aspect and directivity remaining

the same, the radar should be able to detect a target having

four times this radar cross section (Fig. 12) at a range of

about 66 miles. (R

= R

公僒4 ≅ 40 x 1.41 ≅ 66)

Antenna Size. Similarly, the equation enables us to pre-

dict the effects of changes in size of the antenna. Suppose

the antenna is circular and we double its diameter.

Assuming that the aperture efficiency remains the same, this

increase would increase A

by 2

. (A

⬀ d

η.) The range

equation tells us that the increase in A

(Fig. 13) would

increase the range at which the radar might detect a given

target by a factor of two, R

= R

公僒僒僒僒(2

)

= 2R

, provided we

were spotlighting the target.

Doubling the antenna diameter, however, would cut the

beamwidth in half. So, if the radar was searching for targets,

we would have to slow down the antenna scan to maintain

the same time-on-target. If we didn’t, t

would be cut in

half, and the range would be increased by a factor of only

about 1.68. (R

= R

公僒僒僒僒僒僒16 ⫻僒僒僒0.5 ≅ 1.68 R

)

Wavelength. Since wavelength squared is in the denomi-

nator of the equation, decreasing λ would appear to have

the same effect on the radar’s detection range as increasing

the effective area of the antenna, A

But here, an important limitation of our simple equa-

tion shows up. Depending upon what the original wave-

length was and how much we decreased it, the first order

effect of decreasing λ might be offset to a considerable

extent by such factors as increased atmospheric absorption,

one of the factors not accounted for in the equation.

Whereas the range equation indicates that decreasing the

wavelength, λ, from 3 centimeters to 1 centimeter would

increase the radar’s detection range by about 70 percent

(i.e., R

= R

公僒僒僒僒僒僒僒僒1/(

/3)

≅ 1.73), one look at a plot of atmos-

pheric attenuation versus wavelength (Fig. 14) tells us that

this is simply not so.

11. Doubling time-on-target would have the same effect as dou-

bling transmitter power.

12. An increase in radar cross section has the same effect as a

proportional increase in time-on-target.

14. First order effect of decreasing wavelength may be offset by

such factors as increased atmospheric attenuation.