Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

ABRUPT CHANGES OF COEFFICIENTS 199

pressed as

( f ) =

|A( f , n)|

. (13.22)

Since the characteristics of the power spectrum are determined by

the frequency r e sponse function A( f ,n), we can obtain good estimate s of

the time-varying spectru m by controlling the smoothness of A( f ,n). By

considerin g the smoothness of A( f ,n) with respe ct to n, we can obtain

the following mo dels for the change over time of the AR coefﬁcients.

Considering the k-th difference of the A( f ,n) to evaluate the smoo thness

of the change over time of the AR coefﬁcients, we obtain

∆

A( f , n) =

∑

j=1

∆

n j

−2

i j f

. (13.23)

Then, taking the integral of the square of ∆

A( f , n), we obtain

−

|∆

A( f , n)|

d f =

∑

j=1

(∆

)

. (13.24)

Therefore, it is possible to curtail the change over time of the power

spectrum, by reducing the sum of the squares of the k-th differences

of the AR coefﬁcients. Since the squares of the k-th differences of the

AR coefﬁcients add up with the same weights to each term in equation

(13.24), this is equivalent to making the natural assumption that in equa -

tion (13.10),

= ··· =

, (13.25)

and that

∆

= v

n j

, v

n j

∼ N(0,

), j = 1, ···,m. (13.26)

13.5 Abrupt Changes of Co efﬁcients

For the seismic data shown in Figure 13.1, it can be seen that the behavior

of the wave form changes abruptly as a new sig nal arrives at a c ertain

time. In this case, the estimated time-varying coefﬁcients o ften becom e

too variable or too smooth to capture the change of th e characteristics as

seen in Figure 13.2.

In such a case, by applying th e locally stationary AR model shown

in Chapter 8, we can obtain estimates of the change points. By using the

estimates of arrival times of a n ew signal, we may obtain better estimates

200 TIME-VARYING COEFFICIENT AR MODEL

of the time-varying AR coefﬁcients. Abrupt changes are assumed to be

detected at times n = n

,.. ., n

. Corresponding to these points, the noise

term v

n j

of ( 13.10) takes a large negative or positive value. This indica te s

that it is necessary to increase the variance

at the time po ints n =

,.. ., n

Precisely, when

is incr eased in this way, the absolute value of the

k-th time-difference of a

n j

also becomes larger. Thus, for k = 1, the co -

efﬁcient a

n j

shows a stepwise behavior and pr oduces a discontinu ous

point. On the other hand, for k = 2, the slope of a

n j

changes abruptly

and yields a bending point. To yield a jump for a mod el with k ≥ 2, it is

necessary to add noise to each component of the state vector. Therefore,

we ca n realize the jum p e ither by initializing the state and the variance-

covariance matrix x

n|n−1

and V

n|n−1

or by adding a large positive value

to all diagonal elements of V

n|n−1

for n = n

,.. ., n

. T his method is ap-

plicable to trend estimation as well as for the time-varying coefﬁcient

modeling.

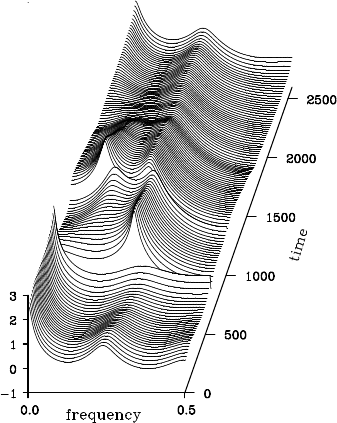
Figure 13.4 Time-varying spectrum estimated by assuming discontinuities in the

parameters.

ABRUPT CHANGES OF COEFFICIENTS 201

Example (Time-varying spectrum with abrupt structural changes)

Figure 13.4 shows the time-varying AR coefﬁcients and the time-varying

spectrum estimated by the model with k = 2 and m = 4 and by assuming

that sudden jum ps occur at n = 630 and at n = 1026, that correspond to

the arrivals of the P-wave and the S-wave, respectively. The estimated

coefﬁcients jump twice at those two points but change very smoothly

elsewhere.

Moreover, from Figure 13.4, we can observe two characteristics

of th e series, ﬁrstly, that the dominant frequencies gradually shift to

the right after the S-wave arrives, and secondly, that the direct current

( f = 0) component increases towards its value in the spectrum of the

backgr ound microtremors.

Problems

1. Give a n example of a heteroscedastic (variance changing over time)

time series o ther tha n earthqua ke data.

2. Co nsider a method of estimating a regression model whose coefﬁ-

cients change over time.

Chapter 14

Non-Gaussian State-Spa ce Mode l

In this chapter, we extend the state-space model to cases where the

system noise and/or the observation noise are non-Gaussian. This non-

Gaussian model is applicable when there are sudden changes in the pa -

rameters caused by structural changes of the system or by outliers in the

time series. For the general non-Gaussian models we consider here, it

may often be the case that w e do not obtain good estimate s of the state

by using Kalman ﬁltering and the smoothing algorithms. E ven in such

cases, however, we can derive a similar exact sequential formula to real-

ize ﬁltering and smoothing algorithms using numerical integration.

14.1 Necessity of Non-G aussian Models

As shown in the previous chapters, various types of time series models

can be expressed in terms of the linear-Gaussian state-space mod el

= Fx

n−1

+ G v

= Hx

+ w

, (14.1)

where y

is the time series, x

is the unknown state vector, and v

and w

are Gaussian white noises.

The state-space model is a very useful tool for time series modeling,

since it is a natural representation of a time series model and provides us

with very efﬁcient computational methods, such as Kalman ﬁltering and

smoothing algorithm s. Although many impo rtant time series models are

expressible as linear-Gaussian state-space models, there are some other

situations where extensions of the model are nec essary, such as the case

of a nonstationary tim e series with time-varying stochastic structure that

sometimes contains both smooth an d abr upt changes. Although a linear-

Gaussian state-space mode l c an reason a bly express gradu a l structural

changes of nonstationary time series, it is necessary to build a complex

model to properly address abrupt ch anges. To remove the inﬂuenc e of

outliers in the da ta , development of an automatic detection method for

203

204 NON-GAUSSIAN STATE-SPACE MODEL

the ou tliers a nd a robust estimation procedu re is necessary (West (1981),

Meinhold and Singpurwalla (1989) and Carlin et al. (1 992)). In addition,

nonlinear systems and discrete proce sses cannot be ad equately modeled

by standard linear Gaussian state-space models.

Let us consider possible solutions to these problems. In state-space

modeling, changes in the stochastic structure are often reﬂected by

changes in the state. Assuming a heavy-tailed distribution such as the

Cauchy distribution for the system noise v

, both smooth changes that

occur with high probability and abrupt cha nges that oc cur with low prob-

ability can be expressed by a single noise distribution.

Similarly, it is reasonable to deal with outliers in time series by us-

ing a heavy-tailed distribution for the observation noise w

. On the other

hand, if the system contains nonlinea rity or if the observations are dis-

crete values, the distribution of the state vector inevitably becomes non-

Gaussian.

Therefore, as a key to the solution of problems that occur with

standard state-space modeling, a treatment of non-Gaussian state dis-

tributions is essential. In the following sections, the recursive ﬁlter and

smoothing algorithms for the estimation of the unknown states of n on-

Gaussian state-space models an d their applications a re presented.

14.2 Non-Gaussian State -Space Models and State Estimation

Consider the following state-sp a ce model

= Fx

n−1

+ Gv

(system mod e l) (14.2)

= Hx

+ w

(observation model) (14.3)

where the system noise v

and the observation no ise w

are white noises

that follow the density functions q(v) and r(w), respe c tively. In contrast

to the state-space models presented in the previous chapters, these distri-

butions are not necessarily Gaussian.

In this case, the distribution of the state vecto r x

generally becomes

non-Gaussian. Consequently, the state-sp ace model of equations (14.2)

and (14.3) is called a non-Gaussian state-space model. Clearly, this non-

Gaussian state-space model is an extension of the standard state-sp ace

model.

As in Chapter 9, the information from the time series obtained by

time j is denoted as Y

≡ {y

,.. ., y

}. Similarly, the set of re alizations

of the state x

up to tim e j is denoted as X

≡ {x

,.. ., x

}. Further, the

initial state vector x

is assumed to be distributed accor ding to the prob-

ability density function p(x

). Here, the state estimation problem is

STATE ESTIMATION 205

to obtain the conditional distribution of the state vector x

, given the in-

formation Y

. There are three versions of the state estimation problem,

depending on the r e la tion between n and m. Speciﬁcally, for n > m, n = m

and n < m, it is called the prediction pro blem, the ﬁltering problem and

the smoothin g problem, respe ctively.

For the linear-Gaussian state-space mode l, the Kalman ﬁlter provides

a recursive algorithm for obta ining the con ditional mean and the condi-

tional variance-covariance matrix of the state vector. On the other hand,

with the general non-Gaussian state-space model, it is necessary to ob-

tain the conditio nal densities for state estimation.

However, f or the state-space models deﬁned by (14.2) and (14.3), by

using the relations p(x

n−1

) = p(x

n−1

) and p(y

n−1

) =

p(y

), we can derive recu rsive formulas for obtaining the one-step-

ahead predictive distribution p(x

n−1

) and the ﬁltering distribution

p(x

) as follows (Kitagawa (1987)). No te that the fo llowing algorithm

can be applied to general nonline a r state-space model (Kitagawa (1991),

Kitagawa and Gersch (1996)).

[ One-step-ahead prediction ]

p(x

n−1

) =

∞

−∞

p(x

n−1

)dx

n−1

∞

−∞

p(x

n−1

)p(x

n−1

)dx

n−1

∞

−∞

p(x

n−1

)p(x

n−1

)dx

n−1

, (14.4)

[ Filtering ]

p(x

) = p(x

n−1

)

p(y

n−1

)p(x

n−1

)

p(y

n−1

)

p(y

)p(x

n−1

)

p(y

n−1

)

, (14.5)

where p(y

n−1

) is obtained as

p(y

)p(x

n−1

)dx

. The one- step-

ahead prediction formula (14.4) is an extension of the one-step-ahead

prediction of the Kalman ﬁlter. He re, p(x

n−1

) is the density function

of the state x

when the previous state x

n−1

is given, which is deter-

mined by the system model (14. 2). Ther e fore, if the ﬁlter p(x

n−1

)

of x

n−1

is given, the one-step-ahead predictor p(x

n−1

) can be evalu-

ated. On the other hand, the ﬁlter formula (14.5) is an extension of the

206 NON-GAUSSIAN STATE-SPACE MODEL

ﬁltering step of the Kalman ﬁlter. p(y

) is the conditional distribu-

tion of the observation y

, when the state x

is given. It is determined by

the ob servation model of (14.3). Therefore, if the predictive distribution

p(x

n−1

) of x

is given, then the ﬁlter density p(x

) is comp utable.

Next, we consider the smoothing proble m. Using the equation

p(x

n+1

) = p(x

n+1

) that h olds for the state-space models of

(14.2) and (14 .3), we obtain

p(x

n+1

) = p(x

n+1

)p(x

n+1

)

= p(x

n+1

)p(x

n+1

)

= p(x

n+1

)

p(x

)p(x

n+1

)

p(x

n+1

)

= p(x

n+1

)

p(x

)p(x

n+1

)

p(x

n+1

)

. (14.6)

Integration of both sides of ( 14.6) yields the following sequential for-

mula for the smooth ing problem:

[ Smoothing formula ]

p(x

) =

∞

−∞

p(x

n+1

)dx

n+1

= p(x

)

∞

−∞

p(x

n+1

)p(x

n+1

)

p(x

n+1

)

n+1

. (14.7)

In the right-hand side of the formula (14.7), p(x

n+1

) is determined by

the system model (14.2). On the other hand, p(x

) and p(x

n+1

) are

obtained by equations ( 14.4) and (14.5), respectively. Thu s, the smooth-

ing formula (14.7) indicates that if p(x

n+1

) is given, we can co mpute

p(x

Since p(x

) can be obtained by ﬁltering (14.5), by re peating the

smoothing for mula (14.7) for n = N −1,...,1 in a similar way as for

the ﬁxed interval smoothing presented in Chapter 9, we can obtain the

smoothing distributions p(x

N−1

),... , p(x

), successively.

14.3 Numerical Computation of the St ate Estimation Formula

As shown in the previous section, we can derive recursive estimation

formu las for the non-Gaussian state-space model that are natural exten-

sions of the Kalman ﬁlter. Adopting this compreh ensive a lgorithm, we

can extensively treat various types of time series mo dels. However, in

NUMERICAL COMPUTATION 207

the practical application of the algo rithm, difﬁculties often arise in cal-

culating the formulas of the ﬁlter and smoother.

For a linear Gau ssian state-space model, all the conditional dis-

tributions p(x

n−1

), p(x

) and p(x

) become normal distribu-

tions. Therefore, in that case, only the mean vectors and the variance-

covariance matrices need to be evaluated, and correspondingly (14.4),

(14.5) and (14.7) become equivalent to the ordinary Kalman ﬁlter and

the smooth ing algorithms. However, since the conditional distribution

p(x

) of the state generally beco mes a non-Gau ssian distribution,

it cannot be speciﬁed using only the mean vector and the variance-

covariance matrix. Various algorithms have been presented, for instance,

the extended Kalman ﬁlter (Anderson and Moore (1979)) and the sec-

ond order ﬁlter, to appr oximate the non -Gaussian distribution by a sin-

gle Gaussian distribution with properly determin ed me an vector and

variance-covariance matrix. In general, however, they do not perform

well.

This section deals with the method of realizing the non-Gaussian ﬁl-

ter an d the non-Gaussian smoothin g algorithm by numerically approx-

imating the non-Gaussian distributions (Kitagawa (1987)). In this ap-

proach , a non-Gaussian state density function is a pproximated numer-

ically using functions such as a step function , a piecewise linear f unc-

tion or a spline. Then, the formulas (14.4)–(14.7) can be evaluated by

numerical computa tion. Since this approach requires a huge am ount of

computation, it used to be considere d an impractical method. Nowadays,

with the development of high-speed com puters, those numerical meth-

ods have beco me practical, at least f or the low-dimensional systems.

In this section, we approximate the density functions that appeared in

(14.4), (14.5) and (14.7) by simple step functions (Kitagawa and Gersch

(1996)).

To be speciﬁc, the de nsity function f (t) to be approximated is de-

ﬁned on a line: −∞ < t < ∞. To approximate th is density functio n by

a step function, the domain o f the density function is ﬁrstly restricted

to a ﬁnite interval [t

], which is then divided into d sub-intervals

< t

< ··· < t

. Here, t

and t

are assumed to be sufﬁciently small

and large nu mbers, respe ctively, and for simplicity, the width of the

sub-intervals is assumed to be identical. Then the i-th point is given by

= t

+ i∆t with ∆t = (t

−t

)/d. In the actual programming of the ends

of the sub-intervals, however, t

and t

change, adapting to changes in

the location of the density fun ction. For simplicity, however, ends of th e

sub-intervals are assumed to be ﬁxed in the following.

In a step-function appro ximation, the f unction f (t) is approximated

208 NON-GAUSSIAN STATE-SPACE MODEL

Table 14.1: Approximation of density functions.

density fun ction approximation denotation

p(x

n−1

) {d;t

,···,t

; p

,···, p

} ˜p(t)

p(x

) {d;t

,···,t

; f

,···, f

}

f (t)

p(x

) {d;t

,···,t

,···, s

} ˜s(t)

q(v) {2d + 1;t

−d

,···,t

−d

,···, q

} ˜q(v)

by f

on the sub-interval [t

i−1

]. If the function f (t) is actually a step-

function, it is given by f

= f (t

). But in general, it may be deﬁne d by

= ∆t

i−1

f (t)dt. (14.8)

Using those values, the step-fu nction approximation o f the function

f (t) is speciﬁed by {d;t

,.. .,t

; f

,.. ., f

}. I n the fo llowing, the a p-

proxim ated function is denoted by

f (t). For the numerical imp le men-

tation of the non-Gaussian ﬁlter and the smoothing formula, it is neces-

sary to approximate the density functions p(x

n−1

), p(x

)

and the system n oise density q(v) as shown in Table 14.1. Here, it is

clear that we should u se the observation noise de nsity r(v) directly,

without discretizing it. Alterna tive approaches for numerical integrations

are Gauss-Hermite polynomial integration (Schnatter (1992)), a r a ndom

replacement of knots spline function approximation (Tanizaki (1993))

and Monte Carlo integration (Carlin et al. (1992), Fr¨uhwirth-Schnatter

(1994), Carter and Kohn (1993)).

In the following, we show a procedure for numerical evaluation of

the simplest one -dimensional trend model:

= x

n−1

+ v

= x

+ w

. (14.9)

[ One-step-ahead prediction ]

For i = 1,... ,d, compute

= ˜p(t

) =

˜q(t

−s)

f (s)ds

∑

j=1

j−1

˜q(t

−s)

f (s)ds