Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

Chapter 13

Time-Varying Coefﬁcient AR Model

There are two typ es of nonstationary time series, one with a drifting

mean value and another which has a structure that varies aroun d the mean

value over time. In the latter type of nonstation ary time series, the vari-

ance, the autocovariance function, and the power spectrum of the time

series change over time.

In this chapter, two m e thods are presented for the analysis o f such

nonstationary time series. One is an estimation me thod for time-varying

variance and the other is a method for modeling the time-varying coefﬁ-

cient AR model. Estimation of the time-varying variance is equivalent to

the estimation of the stochastic volatility in ﬁnancial time series analysis.

Early treatment of AR mode l with time-varying coefﬁcients are reported

in Whittle (1965), Subba Rao (1970) and Bohlin (1976). A state-space

modeling for the time-varying AR model was introduced in Kitagawa

(1983) and Kitagawa and Gersch (19 85,1996). Extension of the state-

space modeling to multivariate time series was shown in Jian g and Kita-

gawa (1993).

13.1 Time-Varying Variance Model

The time series y

, n = 1,. .. ,N is assumed to be a Gaussian white noise

with mean 0 and time-varying variance

. Assuming th a t

2m−1

if we deﬁne a tran sf ormed series s

,.. ., s

N/2

= y

2m−1

+ y

, (13.1)

is distributed as a

-distribution with 2 degrees of freedom, i.e., an

exponential distribution. Therefore, the probability density function of

is given by

f (s) =

−s/2

. (13.2)

189

190 TIME-VARYING COEFFICIENT AR MODEL

The probability density function of the random variable z

deﬁned by

the transformation

= log





, (13.3)

may be expressed as

g(z) =

exp



z −



= exp

(z −log

) −e

(z−log

)

. (13.4)

This means that the transformed series z

can be written as

= log

+ w

, (13.5)

where w

follows a double expone ntial distribution with probability den-

sity func tion

h(w) = exp{w −e

}. (13.6 )

Therefore, an in dependent time series with time-varying variance is

expressed by the state-spa ce model for the trend of the logarithm of the

variance,

∆

= v

= t

+ w

, (13.7)

and the logarithm of the variance of th e original time series y

is esti-

mated by obtaining the trend of the transformed series z

It should be noted that the distribution of the noise w

is not Gaus-

sian. However, since the mean and the variance of the double expon e ntial

distribution are given by −

= 0.57722 (Euler constant) and

/6, re-

spectively, we can approximate it with a Gaussian distribution as follows:

∼ N



−



. (13.8)

(Wahba (1980) used this property in smoothing the log periodogram with

a cross-validated smoo thing spline.) We can estimate the trend t

with

the Kalman ﬁlter. Then t

m|M

with M = N/2 yields a smoothed esti-

mate of log

. In Chapter 14, an exact me thod of estimating the loga-

rithm of the variance will be given, by usin g the exact probability distri-

bution (13.6) and a non-Gaussian ﬁlter and a smoother.

So far, the transformed ser ie s deﬁned as the mean of two consecutive

squared time series sh own in equation ( 13.1) has been used in estimating

TIME-VARYING VARIANCE MODEL 191

Figure 13.1 Estimation of time-varying variance and standardized time series.

From top to bottom: transformed data, estim ated time-varying log-variance and

the normalized time series.

the variance of the time series. This is just to make the noise distribution

g(z) closer to a Gaussian distribution, and it is not essential in estimating

the variance of the time series. In fact, if we use a non-Gaussian ﬁlter

for tre nd estimatio n, we may use the transformed series s

= y

, n =

1,.. .,N, and with this transformation, it is not necessary to assume that

2m−1

Example (Time-varying variance of a seismic data) Figure 13.1

depicts the transformed time series s

obtained using the equation (13.3)

192 TIME-VARYING COEFFICIENT AR MODEL

for the seismic data shown in Figure 1.1, which are estimates of the

logarithm of the variance, log

, and the normalized time series ˜y

n/2

. The parameters of the trend model used for the estimation are

the order of th e trend k, with a value of 2 and the system no ise variance

, with a value of 0.66 ×10

−5

. By this method, we can ob tain a time se-

ries with a variance roughly equal to 1, a lthough the actual seismic data

are not a white noise.

13.2 Time-Varying C oefﬁcient AR Model

The cha racteristics of stationa ry time series can be expressed by an au-

tocovariance f unction or a power spectrum. Therefore, for nonstationary

time series with a time-varying stochastic struc ture, it is natural to con-

sider that its autocovariance function an d power spectrum change over

time. For a stationary time series, its autocovariance function and p ower

spectrum are cha racterized by selecting the o rders and coefﬁcients of

an AR mod el or ARMA model. Therefore, for a nonstationary time se-

ries with a time-varying stochastic structur e, it is natural to consider that

these coefﬁcients and the order of the model change with time.

In this section, an autoregressive model with time-varying coefﬁ-

cients for the nonstationary time series y

is mo deled as

∑

j=1

n j

n−j

+ w

, (13.9)

where w

is a Gaussian white noise with mean 0 and variance

(Kozin

and Nakajima (1980), Kitagawa (1983)).

This model is called the time-varying coefﬁcients AR model of order

m and a

n j

is called the time-varying AR coe fﬁcien t with time lag j at

time n. G iven the time serie s y

,.. ., y

, this time-varying coefﬁcients AR

model contains at least mN unknown coefﬁcients. The difﬁculty with this

type of m odel is, therefore, that we cannot ob ta in meaningful estimates

by applying the maximum likelihood method or the least squ a res method

to the model (1 3.9).

To circumvent this difﬁculty, we apply a stochastic tr end component

model to represent time-varying parameters of the AR model, similar to

the treatment of the trend model and the seasonal adjustment model. For

a trend component model, the trend component t

was assumed to be an

unknown parameter of the model; w e then introduced a model for time-

change of the parameter. Since the AR coefﬁcient a

n j

changes over time

TIME-VARYING COEFFICIENT AR MODEL 193

n, a constraint model

∆

n j

= v

n j

, j = 1 , ... ,m (13.10)

is used where ∆ is the difference operator with respect to the time n,

deﬁned as ∆a

n j

= a

n j

−a

n−1, j

(Kitagawa (1983), Kitagawa and Gersch

(1985, 1996 )).

In (13.10), k is assumed to be 1 or 2. The vector v

= (v

,.. ., v

)

is an m-dimen sional Ga ussian white noise with mean vector 0 and

variance-covariance matrix Q. Since v

and v

n j

are usually assum ed to

be independent for i 6= j, Q become s a diagonal matrix with diagonal el-

ements

,.. .,

; thus, it can be expressed as Q = diag{

,.. .,

It is assumed further in this section that

= ··· =

. The ratio-

nale for the above assum ption will be discussed later in Sec tion 13.4.

Next, to estimate the AR coefﬁcients of the time-varying AR mod el

(13.9) associated w ith the component model (1 3.10), we develop a cor-

respond ing state-space representation. For k = 1 and k = 2 , the state vec-

tors are deﬁned by x

n j

= a

n j

and x

n j

= (a

n j

n−1, j

)

, respectively. T hen

the time-varying coefﬁcient AR model in equation (13.10) can be ex-

pressed as

n j

= F

(k)

n−1, j

+ G

(k)

n j

, (13.11)

where F

(1)

, F

(2)

, G

(1)

and G

(2)

are deﬁned as

(1)

= G

(1)

= 1

(2)



2 −1

1 0



, G

(2)





. (13.12)

Here, assuming the j-th term of equation (13.9) to be the j-th component

of this model, it can be expressed as

n j

n−j

= H

(k j)

n j

, (13.13)

where H

(1 j)

= y

n−j

and H

(2 j)

= (y

n−j

,0). The n the j-th component of

the time-varying coefﬁcient AR model is given by a state-space m odel

with F

(k)

, G

(k)

and H

(k j)

as follows:

n j

= F

(k)

n−1, j

+ G

(k)

n j

n−j

= H

(k j)

n j

. (13.14)

Moreover, noting that H

(1)

= 1 and H

(2)

= (1,0), H

(k j)

is given by

(k j)

= y

n−j

(k)

. (13.15)

194 TIME-VARYING COEFFICIENT AR MODEL

Using the above component mode l, a state-space representation of

the time-varying coefﬁcients AR model is obtained as

= Fx

n−1

+ Gv

= H

+ w

, (13.16)

where, the km × km matrix F, the km × m matrix G and the km-

dimensional vectors H

and x

are deﬁned by

F =







(k)







= I

⊗F

(k)

G =







(k)







= I

⊗G

(k)

= [H

(k1)

,.. ., H

(km)

] = (y

n−1

,.. ., y

n−m

) ⊗H

(k)

(

,.. ., a

)

, for k = 1

n−1,1

,.. ., a

n−1,m

)

, for k = 2

Q =













, R =

. (13.17)

Here, I

is the m ×m un it matr ix a nd ⊗ deno tes the Kronecker prod-

uct of the matrices A and B, i.e., for the k ×ℓ matrix A and th e m ×n

matrix B, A ⊗B is the km ×ℓn matrix whose (i, j) component is given

by a

p+1,r+1

q+1,s+1

for i −1 = pm + q, j −1 = rℓ + s. Hence, the time -

varying coefﬁcients AR model (13.9) and the component m odel for the

time-varying coefﬁcients are expressible in the form of a state-space

model.

For instance, for m = 2 and k = 2, the state-space model is deﬁned







n−1,1

n−1,2













2 −1 0 0

1 0 0 0

0 0 2 −1

0 0 1 0













n−1,1

n−2,1

n−1,2

n−2,2













1 0

0 0

0 1

0 0











TIME-VARYING COEFFICIENT AR MODEL 195

= (y

n−1

, 0, y

n−2

, 0)







n−1,1

n−1,2







+ w

(13.18)



n,1

n,2



∼ N









, w

∼ N(0,

The above state-space model c ontains several unknown parameters.

For these parameters, since the log-likelihood function can be computed

by the m ethod presented in Chapter 9, the variance

of the observation

noise w

and the variance

of the system noise v

can be estimated by

the maximum likelihood method. The AR orde r m and the order k of the

smoothne ss ca n be determin ed by minimizing the information criterion

AIC. Given the orders m and k and the estimated variances

and

the smoothed estimate of the state vector x

n|N

is obtained by th e ﬁxed

interval sm oothing algorithm. T hen, the (( j −1)k + 1)

element of the

estimated state gives the smoothed estimate of the unknown time-varying

AR coefﬁcient ˆa

n, j|N

Storage of size mk ×mk ×N is necessary to obtain the smoothed esti-

mates of these time- varying AR coefﬁcients simultaneously. If either the

AR order m or the series length N is large, the necessary memory size

may exceed the memory of the computer and may m a ke the computa-

tion impossible. Making an assumption that the AR coefﬁcients change

only once every r time-steps for some integer r > 1 may be the simplest

method of mitigating such me mory problems of th e computin g facilities.

For example, if r = 20, the necessary memory size is obviously reduced

by a factor of 20. If the AR coefﬁcients change slowly and gradually,

such an approximation has only a slight effect on the estimation of coef-

ﬁcients. To execute the Kalman ﬁlter and smoother for r > 1, we repeat

the ﬁltering step r times at each step of the on e-step-ahead prediction.

Example (Time-varying coefﬁcient AR models for seismic data)

Table 13.1 summarizes the AIC’s of time-varying coefﬁcient AR models

ﬁtted to the normalized seismic data shown in Figure 13.1, with various

orders obtained by putting r = 20.

Since the observation noise variance

is assumed to be a c onstant

in the TV CAR modeling, if the variance of the time series signiﬁcantly

changes as can be observed in Figure 1. 1(f), it is better to ﬁt the model to

a transformed time series. For instance, Figure 13.1 shows that the vari-

ance of th e time series is approximately homoscedastic. For this data, the

AIC was minimized at m = 8 for k = 1 and m = 4 for k = 2.

196 TIME-VARYING COEFFICIENT AR MODEL

Table 13.1 AIC’s of time-varying coefﬁcients AR models ﬁtted to normalized

seismic data.

m k = 1 k = 2 m k = 1 k = 2

1 6492.5 6520.4 6 4831.9 4873.8

2 5527.7 5643.2

7 4821.6 4878.7

3 5070.0 5134.5 8 4805.1 4866.9

4 4820.0 4853.9 9 4813.4 4884.9

5 4846.0 4886.0

10 4827.1 4911.9

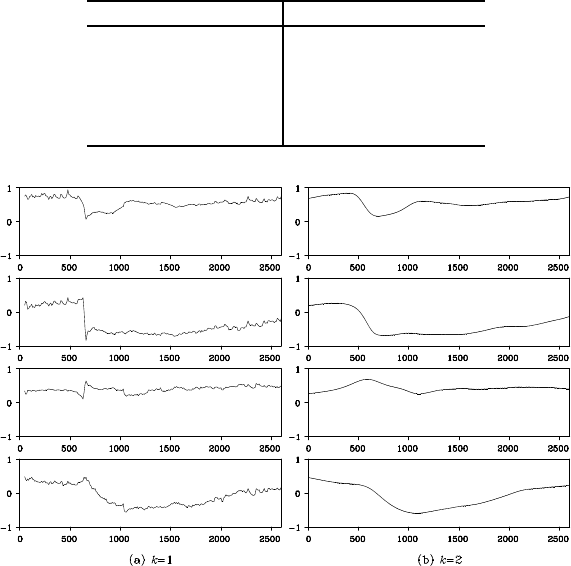
Figure 13.2 Estimated time-varying PARCOR for the normalized seismic data.

Only the ﬁrst four PARCOR’s are shown. Left plots: k = 1, right plots: k = 2.

Horizontal axis: time point, vertical axis: value of PARCOR.

Figure 13.2 shows the time-varying coefﬁcients in the case of the

TVCAR models with the AIC best ﬁt orders m for k = 1 and k = 2. Note

that the ﬁgure depicts the time-varying PARCORs b

for i = 1, 2,3, 4,

instead of the AR c oefﬁcients. The p lots on the lef t-hand side are for

the case of k = 1 and on the right-hand side are fo r the case of k = 2.

From the ﬁgure, we see that the estimated coefﬁcients vary with time

correspo nding to the arrivals of the P-wave and the S-wave at n = 630

and n = 1026, respectively, which were estimated by using the locally

stationary AR model. In Figure 13.2, the estimates using k = 2 are very

ESTIMATION OF THE TIME-VARYING SPECTRUM 197

smooth. However, as is apparent in the ﬁgure, the estimates with k = 2

do not appropriately correspond to the a brupt changes of the time series

that correspond to the arrival of the P-wave an d the S-wave. Compared

with this, the estimates obtained from the TVCAR model with k = 1 are

variable. According to the AIC criterio n, the TVCAR mod e l with k = 1

is considered to be a better model than that with k = 2. In Sectio n 13.5,

we shall consider a method for obtainin g smooth estimates tha t has the

capacity to adapt to abrupt structural changes.

13.3 Estimation of the Time-Varying Spectrum

For a statio nary AR model, the power spectrum is given by

p( f ) =



1 −

∑

j=1

−2

i j f



, −

≤ f ≤

. (13.19)

Therefore, in the case that the AR co e fﬁcients at time n are given by

n j

for the time-varying c oefﬁcient AR model (13.9), the instantane ous

spectrum at time n can be deﬁned by

( f ) =



1 −

∑

j=1

n j

−2

i j f



, −

≤ f ≤

. (13.20)

Using the time-varying AR coefﬁcients a

n j

introdu ced in the pre-

vious section, we can estimate the time-varying power spe ctrum as a

function of time, which is called the time-varying spectrum.

Example ( Time-varying spectrum of a seismic data) Figure 13.3

illustrates the time-varying spectrum obtained from the equation (13 .20).

The left plot shows the case for k = 1, and th e right plot shows the case

for k = 2. In the plots of Fig ure 13.3, the horizontal and the vertical

axes indicate the frequency and the logarithm of the spe ctra, respectively,

and the slanted axis indicates time. From the ﬁgures, it can be seen that

the power of the spectrum arou nd f = 0.25 increa ses with the arr ival of

the P-wave. Subsequently, the power aro und f = 0.1 in creases w ith the

arrival of the S-wave. After that, the pe a ks of the spectra gradually shift

to the right, and the spectrum eventually converges to that of the original

backgr ound motions.

198 TIME-VARYING COEFFICIENT AR MODEL

Figure 13.3: Time-varying spectra of a seismic data.

13.4 The Assumption on Syste m No ise for the Time-Vary ing

Coefﬁcient AR Model

As stated in Section 13.2, the time-varying AR coefﬁcients can be es-

timated by approximating the time-change of AR coefﬁcients using the

trend component models and th en the TVCAR model can be expressed

in a state-spac e form. In the state-space model (13.17), the variance-

covariance matrix for the system noise is assumed to be a diagonal form

given by Q = diag



,···,



. T his seems to be a very strong assump-

tion; however, in this section, it will be shown that it arises naturally,

by considering the smoothne ss of the frequency r esponse function of the

AR operator.

Firstly, we consider th e Fourier transform of the AR coefﬁcients of

the TVCAR model,

A( f , n) = 1 −

∑

j=1

n j

−2

i j f

, −

≤ f ≤

. (13.21)

This is the frequency response f unction of th e AR model considered as

a whitening ﬁlter. Then the time-varying spectrum of (13.20) can be ex-