Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

Chapter 11

Estimation of Trends

In econo mic time series, we frequently face long-lasting increasing or

decreasing trends. In this chapter, we initially c onsider a polynomial re-

gression model to analyze time series with such tendencies. Secondly,

we sha ll introd uce a trend model to estimate a complicated tren d that we

cannot express in terms of a simple parametr ic mode l such as a poly-

nomial or trigonometric regression model. The tr e nd component mo del

treated in this chapter, representing stoc hastic changes of parameters,

forms a framework for modeling various types of nonstationary time se-

ries that will be introduced in succeeding chapters.

11.1 The Polynomial Trend Model

The WHARD data in Figure 1.1 (e) show a tendency to increase over

the entire time domain. Such a long-te rm tendency often seen in eco-

nomic time series such as the one depicted in Figure 1.1(e) is called

trend. Needless to say, estimating the trend of such a time series is a very

natural way o f capturing the tendency of the tim e series and predicting

its future behavior. However, even in the case of analyzing short-term

behavior of a time series with a trend, we often analyze the time series

after removing the trend, because it is not appropriate to directly apply a

stationary time series model such as the AR model to the original series.

In this section, we shall explain the polynomial regression model as a

simple tool to estimate the trend of a time series.

For the polynomial regression model, the time ser ie s y

is expressed

as the sum of the trend t

and a residual w

= t

+ w

, (11.1)

where w

follows a Gaussian distribution with mean 0 and variance

It is assumed that the trend com ponent can be expressed as a polynomial

= a

+ a

+ ···+ a

. (11.2)

159

160 ESTIMATION OF TRENDS

Since the above polynomial regression model is a special case of the

regression model, we can easily estimate the model by the method shown

in Chapter 5. That is, to ﬁt a polynomial trend model, it sufﬁces to d eﬁne

the j-th explan atory variable as x

n j

= x

j−1

, and construct the matrix X

X =







1 x

··· x

1 x

··· x







(11.3)

Then, by reducing the matrix X to upper triang ular form by an ap-

propriate Householder transfor mation U ,

UX =











··· s

1,m+2

m+2,m+2







, (11.4)

the residual variance of the polynomial r egression model of order j is

obtained as

m+2

∑

i= j+2

i,m+2

. (11.5)

Since the j-th order model has j + 2 parameters, i.e ., j +1 regression

coefﬁcients and the variance, the AIC is obtained as

AIC

= N log 2

+ N + 2( j + 2). (11.6)

The AIC best order is then obtained by ﬁnding the minimum o f the AIC

Given the AIC best orde r j, the maximum likelihood estimates ˆa

,···, ˆa

of the regression coefﬁcients are obtained by solving th e system of linear

equations







··· s

1, j+1

j+1, j+1

























1,m+2

j+1,m+2







. (11.7 )

Here, since the matrix S is in upper triangular f orm, this system of linear

equations can be easily solved by backward substitution.

Example (Maximum temperature data) Tab le 11.1 summarizes the

residual variance

and the AIC

values of the polyn omial regression

models ﬁtted to the maximum tem perature data shown in Figure 1.1(c).

THE POLYNOMIAL TREND MODEL 161

Table 11.1 Maximum temperature data: The residual variances and AIC values

of the polynomial regression models.

AIC

0 60.09 1 996.55 4 10.18 1141.74

1 58.89 1 988.81 5 9.64 1 117.51

2 33.61 1 718.14

6 8.97 1084.22

3 23.74 1 551.26 7 8.96 1 085.90

Table 11.2 (L og) WHARD data: The residual variances and AIC values of the

polynomial regression models.

AIC

0 0.02752 −550.91 8 0.00115 −1027.44

1 0.00163 −986.60 9 0.00112 −1029.21

2 0.00150 −998.22

10 0.00107 −1033.60

3 0.00149 −996.98 11 0.00107 −1031.65

4 0.00147 −997.43

12 0.00106 −1031.51

5 0.00142 −1000.63 13 0.00106 −1029.62

6 0.00123 −1021.24 14 0.00105 −1029.76

7 0.00122 −1019.98

15 0.00102 −1032.34

As shown in Table 11.1, the AIC was minim iz e d at order 6, although th e

residual variance

decreases monotonically.

Similarly, Table 11.2 shows the results for the logarithm of the

WHARD data. In this example, although the residual variance decreases

as the orde r increases, the AIC was minimized at order 10.

Plots (a) and (b) of Figure 11.1 show the original time series and the

trends estimated using the AIC best polynomial regression models. In

plot (a) of the ma ximum temperature da ta , a gradual and smooth change

of temperature is reasonab ly captured by the estimated trend. Also in the

case of the logarithm of the WHARD data, plot (b) shows a generally

smoothly changing trend. In this case, however, we see that the estimated

trend c hanges too rapidly at the start of the series. Moreover, the abrupt

drop in sales in 197 4 and 1975, which corresponds to n around 95 in plot

(b), is not clear ly detected. We shall consider a method to solve these

problems later in Section 11.3.

162 ESTIMATION OF TRENDS

Figure 11.1 Trends of maximum temperature data and WHARD data estimated

by the polynomial regression model.

11.2 Trend Component Model–Model for Probabilistic Structural

Changes

The polynomial trend model treated in the previous section can be ex-

pressed as

∼ N(t

). ( 11.8)

For this model, it is assumed that the time series is distributed as a nor-

mal distribution with mean value given by the polynomial t

and constant

variance

This type of parametric model can yield a good estimate of the trend,

when the actual trend is a polynomial or can be closely approximated

by a polyn omial. However, in other cases, a parametric mo del may no t

reasonably c apture the characteristics of the trend or it may become too

sensitive to random noise.

TREND COMPONENT MODEL 163

Consider a polynomial of the ﬁrst order, i.e., a straight line, given by

= an + b. (11.9)

Here, if we deﬁne the time shift operator ∆ b y ∆t

≡ t

−t

n−1

, then we

have

∆t

= a, ∆

= 0. (11.10)

This means that the ﬁrst ord e r polynomial is the solu tion of the initial

value pro blem for the seco nd order difference equation

∆

= 0, ∆t

= a, t

= b. (11.11)

In general, a polynomial of order k −1 can be considered a solution of

the difference equation of order k,

∆

= 0. (11.12)

In ord er to make the polynomial more ﬂexible, we assume that ∆

≈

0 instead of using the exact difference equation (11.12). T his can be

achieved by introducing a stochastic difference equation of order k,

∆

= v

, (11.13)

where v

is assumed to be a white noise th a t follows a normal distribu-

tion with mea n 0 and variance

,N(0,

). In the following, we call the

model (11.13) a trend component model ( Kitagawa and Gersch (198 4,

1996). Because the solution of the difference equation ∆

= 0 is a

polynomial of order k −1, the trend comp onent m odel of order k can

be considered a s an extension of a polynomial of order k −1. When the

variance

of the noise is small, the realization of a trend componen t

model locally becomes a smooth function that resembles the polyno-

mial. However, a remarkable difference from the polynomial is that the

trend component mod el can express a very ﬂexible function globally.

Example (Random walk model) For k = 1, this model becomes a

random walk model which can be deﬁned by

= t

n−1

+ v

, v

∼ N(0,

). (11.14)

This model expresses that the trend is locally constant an d c an be ex-

pressed as t

≈t

n−1

For k = 2, the trend component model becomes

= 2t

n−1

−t

n−2

+ v

(11.15)

164 ESTIMATION OF TRENDS

for which it is assumed that the trend is locally a linear function and sat-

isﬁes t

−2t

n−1

n−2

≈0. In general, the k-th order difference o perator

of the trend component model (11.13) is given by

∆

= (1 −B)

∑

i=0

(−B)

. (11.16)

Therefore, using the binomial coefﬁcient c

= (−1)

i+1

, the tren d

component mod e l of order k can be expressed as

∑

i=1

n−i

+ v

. (11.17)

Note tha t c

= 1 for k = 1 and c

= 2 and c

= −1 for k = 2. Although

these models ar e not stationary, they can formally be consid e red as AR

models of order k, by deﬁning the state vector x

and F, G and H as







n−1

n−k+1







, F =







··· c







, G =













H = [ 1 0 ··· 0 ], (11.18)

thus leading to a state-space re presentation of the trend model,

= Fx

n−1

+ Gv

= Hx

. (11.19)

Example (State-space representation of trend models) For k = 1,

the state-space mode l is obtained by putting

= t

, F = G = H = 1. (11.20)

For k = 2, the state-space models of the trend models are obtained by



n−1



, F =



2 −1

1 0



, G =





, H = [ 1 0 ]

(11.21)



−t

n−1



, F =



2 1

−1 0



, G =





, H = [ 1 0 ].

(11.22)

TREND MODEL 165

Note that the model (11.22) yields the can onical representation of the

trend model treated in Chapter 9. Moreover, for k = 2, the state vector

may alternatively be deﬁned as x

= (t

)

F =



1 1

0 1



, G =





, H = [ 1 0 ]. (11.23)

Since

≡ ∆t

holds for this model, we ca n easily conﬁrm that it is

equivalent to the model (11.21). The advantage of using this representa-

tion is that it can easily be gener alized (Harvey (1989)); we can extend

the trend component model by setting





, F =



1 1

0 1



, G =



1 1

0 1



, H = [ 1 0 ]. (11.24)

Here, the trend component satisﬁes

n−1

+ v

= t

n−1

+ v

(11.25)

= t

n−1

+ v

In contrast to the ordinary trend mod e l with one-dimensional system

noise, in this case, we have ∆t

+ v

. This extended tre nd m odel

has th e characteristic of allowing both level an d slope to have indepen-

dent noises, thus expressing a more ﬂexible trend compo nent.

11.3 Trend Model

A trend in a time series expresses a rough tendency of the phenomenon.

In other words, an ac tually o bserved time series represents a superposi-

tion of a trend and various variations around it. Here, we consider th e

simplest case where the time series is expressed as

= t

+ w

, (11.26)

where w

is a white noise. This is the simplest model tha t expresses a

generating mechanism for observations; it can be considered as a special

form of the observation model given in Chapter 9.

To estimate the trend com ponent t

from the time series y

, we co n-

sider the following trend model that consists of the trend component

model and the above observation model,

∆

= v

(11.27)

= t

+ w

. (11.28)

166 ESTIMATION OF TRENDS

Here, v

is similar to (11.13), a Gaussian white noise with m ean 0 and

variance

, and w

is a Gaussian white noise with mean 0 and variance

The observation m odel in equation (11.28), y

= t

+ w

, is assumed

to express the condition that the time series y

is obtained by adding an

indepen dent noise to the trend. On the other hand, the trend co mponent

model (11.27) expresses the change in the trend. Actual time series are

usually not as simple as this; they o ften require more sophisticated mod-

eling and this will be treate d in the next chapter. Based on the state-space

representation of the trend componen t model, the state-space represen-

tation of the trend model is as follows:

= Fx

n−1

+ Gv

= Hx

+ w

, (11.29)

where the state vector x

is an appropriately deﬁned k-dimensional vec-

tor, and F, G and H are th e k ×k matrix, the k-dimensional column vecto r

and th e k-dim ensional row vector determined by (11.27) and (11.28), re-

spectively. This mode l differs from the trend compo nent model (11.18)

only in that it contains an additional observation no ise. As an exam ple,

for k = 2, the matrice s and vectors above are deﬁned by



n−1



, F =



2 −1

1 0



, G =





(11.30)

H = [ 1 0 ].

Once the order k of the trend mod e l and the variances

and

have

been speciﬁed, the smoothed estimates x

1|N

,···, x

N|N

are obtained by the

Kalman ﬁlter and the ﬁxed-interval smoothing algorithm presented in

Chapter 9 . Since the ﬁrst component of the state vector is t

, th e ﬁrst

component of x

n|N

, namely, Hx

n|N

, is the smoothed estimate of the trend

n|N

Example (Trend of maximum temperature data) Figure 11.2

shows various estimates of the tren d of the max imum temperature data

obtained by changing the variance of the system noise

for th e ﬁrst

order trend model, k = 1. The variance of the observation noise

estimated by the maximum likelihood method. Plot (a) shows the ca se of

= 0.223 ×10

−2

. The estimated trend reason ablly captures the annual

cycles of the temperature data. In plot (b) where the model is k = 1 and

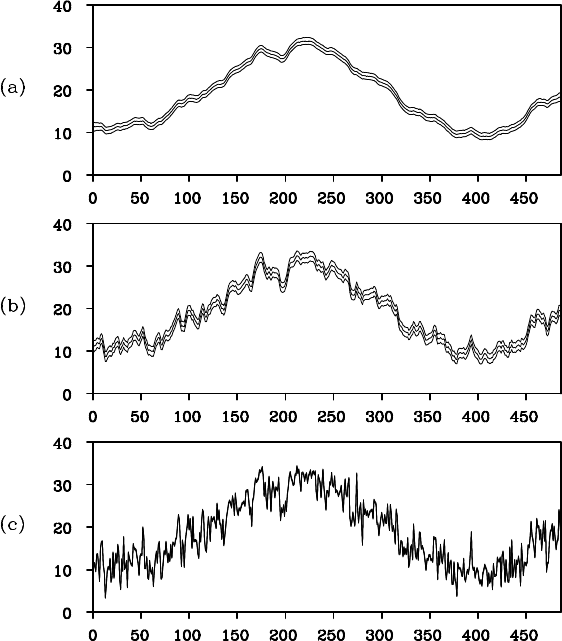
TREND MODEL 167

Figure 11.2 Trend of the temperature data obtained by the ﬁrst order t rend mod-

els.

= 0.223, the estimated trend reveals more detailed changes in tem-

perature. Plot (c) shows the case of k = 1 a nd

= 0.223 ×10

. The

estimated trend just follows the observed time series.

On the other hand, Figure 11.3 shows the estimated trends ob-

tained by the models with k = 2. The estimated trend in (a) obtained

= 0.321 ×10

−5

is to o smooth and th e estimated trend in (c) ob-

tained by

= 0.0321 becomes an undulating curve. But in plot (b), it is

evident that the estimate obtained by

= 0.321 ×10

−3

yields a reason-

able trend. Comparing Figures 11.2 (a) and (b) with Figure 11.3 (b), we

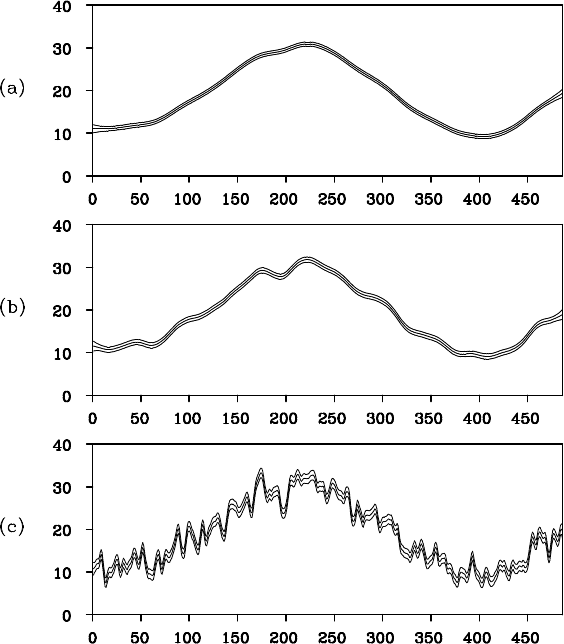
168 ESTIMATION OF TRENDS

Figure 11.3 Trend of temperature data obtained by the second order trend mod-

els.

can see that the second order trend model yields a considerably smooth e r

trend. As shown in the above examples, the trend model contains the or-

der k and the variances

and

as parameters, which yield a variety of

trend estimates. To o btain a good estimate of the trend, it is necessary to

select appropriate parameters.

The e stima tes of the variances

and

are obtain ed by the ma x-

imum likelihood method. Using the method shown in Subsection 9.6,

however, if the ratio

is speciﬁed, the estimate of

is auto-

matically obtained. Therefore, the estimate of the trend is controlled by