Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

STATE ESTIMATION VIA THE KALMAN FILTER 139

1|0

→ x

2|0

→ x

3|0

→ x

4|0

→ x

5|0

→

⇓

1|1

⇒ x

2|1

→ x

3|1

→ x

4|1

→ x

5|1

→

⇓

1|2

← x

2|2

⇒ x

3|2

→ x

4|2

→ x

5|2

→

⇓

1|3

← x

2|3

← x

3|3

⇒ x

4|3

→ x

5|3

→

⇓

1|4

← x

2|4

← x

3|4

← x

4|4

⇒ x

5|4

→

⇓

Figure 9.1 Recursive computation by the Kalman ﬁlter and smoothing algo-

rithm. ⇒: prediction, ⇓: ﬁlter, ←: smoothing, →: increasing horizon prediction.

[One-step-ahead prediction]

n|n−1

= F

n−1|n−1

n|n−1

= F

n−1|n−1

+ G

. (9.12)

[Filter]

= V

n|n−1

n∗n−1

+ R

)

−1

n|n

= x

n|n−1

+ K

−H

n|n−1

) (9.13)

n|n

= (I −K

n|n−1

In the algorithm for one-step-ahead prediction, the predictor (or

mean) vector x

n|n−1

of x

is obtained simply by multiplying the tran-

sition matrix F

by the ﬁlter of x

n−1

, x

n−1|n−1

. Moreover, the variance-

covariance matrix V

n|n−1

consists of two terms; the ﬁrst te rm expresses

the inﬂuence of the transformation by F

, and the second shows the inﬂu-

ence of the system noise v

. In the ﬁlter algorithm, the Kalman gain K

initially obtained. The prediction error of y

and its variance-covariance

matrices are obtained as y

−H

n|n−1

and H

n|n−1

+ R

, r e spec-

tively. Here, the mean vector of the ﬁlter of x

can be obtained as the

sum of the prediction vector x

n|n−1

and the prediction error multiplied

by the Kalman gain. Then, since x

n|n

can be re-expre ssed as

n|n

= K

+ (I −K

n|n−1

it can b e seen that x

n|n

is a weighted sum of the new observation y

and

the predicto r, x

n|n−1

140 ANALYSIS OF TIME SERIES WITH A STATE-SPACE MODEL

Next, V

n|n

can be written as

n|n

= V

n|n−1

−K

n|n−1

Here, the second term of the right-h and side shows the improvement in

accuracy of the state estimation of x

, resulting from the information

added by the new observation y

9.3 Smoothing Algorithms

The problem of smoothing is to estimate the state vector x

based on the

time series Y

= y

,···,y

for m > n. There are th ree types of smoothing

algorithm . If m = N, the smoothing algorithm estimates the state based

on the entire set of observations and is called ﬁxed-interval smooth ing. If

n = m −k, it always estimates the state k steps before, and is ca lled ﬁxed-

lag smoothin g. If n is set to a ﬁxed time point, e.g., n = 1, it estimate s a

speciﬁc point, such as the initial state, and is called ﬁxed-point smooth-

ing. Compared with the ﬁltering algorithm that uses the observations up

to time n for e stima tion of the state x

, ﬁxed-interval smoothing yields a

more accurate estimate of th e state x

, by using all available data.

Fixed-interval smoothing

= V

n|n

n+1

−1

n+1|n

n|N

= x

n|n

+ A

n+1|N

−x

n+1|n

) (9.14)

n|N

= V

n|n

+ A

n+1|N

−V

n+1|n

As shown in this algorithm, the ﬁxed-interval smoo thing estimates,

n|N

and V

n|N

, can be derived from results obtained by the Kalman ﬁl-

ter, i.e., x

n|n−1

, x

n|n

, V

n|n−1

and V

n|n

. T herefore, to perform ﬁxed-interval

smoothing, we initially obtain x

n|n−1

n|n

n|n−1

n|n

, n = 1, ···,N by

the Kalman ﬁlter and compute x

N−1|N

, V

n−1|N

through x

1|N

, V

1|N

back-

ward in time (see Figure 9.1). It should be noted that the initial values

N|N

and V

N|N

necessary to perfo rm the ﬁxed-interval smoothing algo-

rithm can be obtained by the Kalman ﬁlter.

9.4 Increasing Horizon Prediction o f the State

It will be shown that by repeating one-step-ahead prediction by means of

the Kalman ﬁlter, we can perform increasing horizon prediction, tha t is,

to obtain x

n+k|n

and V

n+k|n

for k = 1,2,···. Let us co nsider the problem

of estimating the increasing horizon prediction, i.e., estimating the state

PREDICTION OF TIME SERIES 141

n+ j

for j > 1 based on the time series Y

= y

,···, y

. Firstly, the mea n

vector x

n+1|n

and th e variance-covariance matrix V

n+1|n

of the one-step-

ahead predictor of x

n+1

are obtained by the Kalman ﬁlter. Here, since the

future observation y

n+1

is u navailable, it is assumed that Y

n+1

= Y

. In

this case, we have that x

n+1|n+1

= x

n+1|n

and V

n+1|n+1

= V

n+1|n

. There-

fore, from the one- step-ahead prediction algorithm of the K alman ﬁlter

for the period n + 1, we have

n+2|n

= F

n+2

n+1|n

n+2|n

= F

n+2

n+1|n

n+2

+ G

n+2

. (9.15)

This means that two-step-a head prediction can be realized by repeat-

ing the prediction step of the Kalman ﬁlter twice without the ﬁltering

step. In general, j-step-ahead prediction based on Y

can be performed

using the relation that Y

= Y

n+1

= ··· = Y

n+ j

, by repeating the predic-

tion step j times. Summarizing the above, the algorithm for the increas-

ing horizon prediction x

n+1

,···, x

n+ j

based on the observation Y

can be

given as follows:

The increasing horizon prediction

For i = 1,···, j, repeat

n+i|n

= F

n+i

n+i−1|n

n+i|n

= F

n+i

n+i−1|n

n+i

+ G

n+i

. (9.16)

9.5 Prediction of Time Series

Future values of time series can be imm ediately predicted by using the

predicted state x

obtained as shown above. When Y

is given, from

the re lation between the state x

and the time series y

, which is ex-

pressed by the observation model (9.2), the mean and the variance-

covariance m a trix o f y

n+ j

are denoted by y

n+ j|n

≡ E(y

n+ j

) and

n+ j|n

≡ Cov(y

n+ j

), respectively. Then, we can obtain th e mean and

the variance-covariance matrix of the j-step-ahead predictor of the time

series y

n+ j

n+ j|n

= E (H

n+ j

+ w

n+ j

)

= H

n+ j

n+ j|n

(9.17)

n+ j|n

= Cov(H

n+ j

+ w

n+ j

)

= H

n+ j

Cov(x

n+ j

+ H

n+ j

Cov(x

n+ j

)

+ Cov(w

n+ j

+ Cov(w

n+ j

)

= H

n+ j

n+ j|n

n+ j

+ R

n+ j

. (9.18)

142 ANALY SIS OF TIME SERIES WITH A STATE-SPACE MODEL

As indic ated previously, the p redictive distribution of y

n+ j

based on

the observation Y

of the time series becomes a nor mal distribution with

mean y

n+ j|n

and variance-covariance matrix d

n+ j|n

. These are easily ob-

tained by (9.17) and (9 .18). That is, the mean of the predictor of y

n+ j

given by y

n+ j|n

and the standard error is given by (d

n+ j|n

)

1/2

. It should

be noted that the one-step-ahead predictor y

n|n−1

and d

n|n−1

of the time

series y

have already b e en ob ta ined and were applied in the algorithm

for the Kalman ﬁlter (9.13).

Example (Increasing horizon prediction of BLSALLFOOD data)

Figure 9.2 sh ows the results of the increasing horizon prediction of the

BLSALLFOOD data, N = 156. In this p rediction, the AR model was

ﬁtted to the initial 120 observations and the estimated AR mo del was

used f or increasing horizon prediction of the succeeding 36 observations,

121

,···, y

156

. In the estimation of the AR model, we ﬁrstly obtain a time

series with mean zero, y

∗

by de leting the sample mean, ¯y of the time

series,

∗

= y

− ¯y,

and then the parameters of the A R model a re obtained by applying the

Yule-Walker method to the time series y

∗

,···, y

∗

The increasin g horizon prediction of the time series y

∗

n+ j|n

is obtained

by applying the Kalman ﬁlter to the state-space representation of th e AR

model; the increa sing horizon prediction value of the time series y

n+ j

then obtain ed by

n+ j|n

= y

∗

n+ j|n

+ ¯y.

Figure 9.2 shows th e mean y

120+ j|120

, j = 1,···,36, and its ±1 stan-

dard error interval y

120+ j|120

of the p redictive distribution

obtained by this method. The actual time series is indicated by a solid

curve for n ≤ 12 0 and by the symbol ◦ for n > 120 .

Plots (a), (b), (c) and (d) show the results o f the increasing ho rizon

prediction obtained by AR mo dels of orders m = 1, 5, 10 and 15, re-

spectively. In the case of the ﬁrst order AR model shown in plot (a),

the increasing horizon p rediction value rapidly attenuates exponentially,

which indicates that the information on the periodic behavior of this data

is not effectively used for the prediction. In the case of m = 5 shown in

plot (b), the pr edictor reasonably reproduced the cyclic behavior for the

ﬁrst year, but after one year passed, the predicted value rapidly decayed.

The predictors for the AR model with m = 10 repr oduce the actual be-

havior of the time series relatively well. Finally, the predic tors for the AR

model with m = 15 accurately reproduce the details of the wave form of

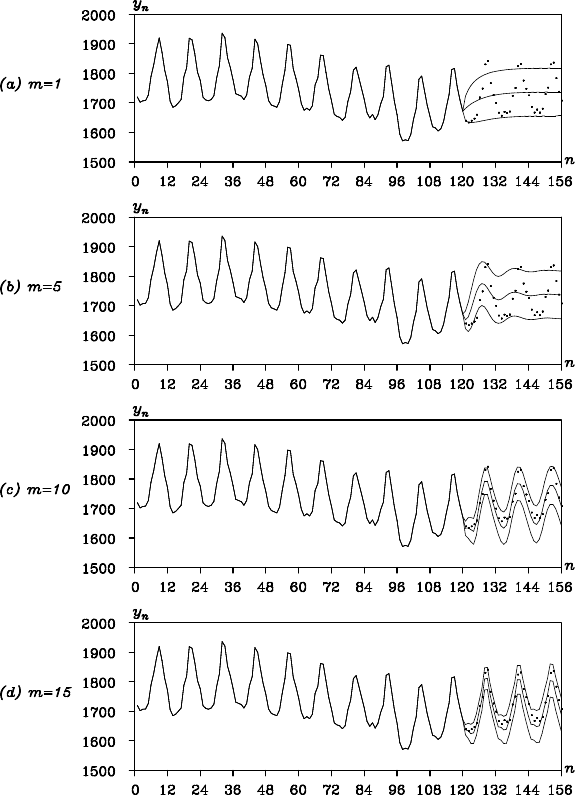
PREDICTION OF TIME SERIES 143

Figure 9.2 Increasing horizon predictive distributions (bold l ine: mean, thin

line: ± (standard deviation) and ◦: observed value). Orders of the AR models

are 1, 5, 10 and 15, respectively.

144 ANALY SIS OF TIME SERIES WITH A STATE-SPACE MODEL

the actual time series. In contrast to the one-step-ahead prediction, the

increasing horizon prediction may lead to sig niﬁcant differences among

the results from AR models of different assumed orders. These re sults

indicate that prediction by a model of improper order may yield such an

inappropriate prediction that appropriate model selection is extremely

important for the increasing horizon prediction.

9.6 Likelihood Computation and Parameter Estimation for a

Time Series Model

Assume that the state-space representation for a time series model spec-

iﬁed by a parameter

is given. When the time series y

,···, y

of length

N is given, the N dimensional joint density function of y

,···, y

speci-

ﬁed by this time series model is denoted by f

,···, y

). Th en, the

likelihood of this model is deﬁned b y

) = f

,···, y

). (9.19)

By repeatedly applying th e r elation

,···,y

) = f

n−1

,···, y

n−1

,···, y

n−1

for n = N, N −1,···, 2, the likelihood of the time series model can be

expressed as a product of con ditional density f unctions:

) =

∏

n=1

,···, y

n−1

) =

∏

n=1

n−1

). (9.20 )

For simplicity of notation here, we let Y

= ∅ (empty set) and then

) ≡ g

). By taking the logar ithm of L(

), the log-

likelihood of the model is obtaine d as

ℓ(

) = log L(

) =

∑

n=1

log g

n−1

). (9.21)

As shown in (9.17) and (9.18), since g

n−1

) is the conditional

distribution of y

given the observation Y

n−1

and it is, in fact, a normal

distribution with mean y

n|n−1

and variance-covariance matrix d

n|n−1

, it

can be expressed as (Kitagawa and Gersch (1996))

n−1

) =



√



ℓ

n|n−1

−

×exp



−

−y

n|n−1

)

−1

n|n−1

−y

n|n−1

)



.(9.22)

LIKELIHOOD AND PARAMETER ESTIMATION 145

Therefore, b y substituting this d ensity function into (9.21), the log-

likelihood of this state-space model is obtained as

ℓ(

) = −



ℓN log 2

∑

n=1

log|d

n|n−1

∑

n=1

−y

n|n−1

)

−1

n|n−1

−y

n|n−1

)



. (9.23)

Stationary time series models such as the AR models, the ARMA

models and many other nonstationary tim e series models such as trend

and seasonal adjustme nt models can be expressed in the f orm of linear

Gaussian state-space mo dels. Accordingly, for such tim e series mode ls,

a uniﬁed algorithm for computing the log-likelihood can be obtained by

using the Kalman ﬁlter and (9.23). Th e maximum likelihood estimates

of the parame ters of the time series model can be obtained by ma ximiz-

ing this log-likelihood b y a numerical optimization method, which will

be described later in Appendix C. Examples of parameter estimation for

state-space models are described in Ch a pter 1 0 to Chapter 15.

In this way, the parameters c ontained in the state-space model can

be estimated b y numerical ma ximization of the log -likelihood of ( 9.23),

but this generally requires considerable computation. Therefore, if the

maximum likelihood estimate or a good app roximation can be o btained

analytically, this method should be used for efﬁcient estimation. For in-

stance, on the assumption that there is no missing observation in esti-

mating an AR model, we should use the Yule-Walker method, the least

squares method or the PARCOR method, which have been shown in

Chapter 7, rath er than the above method. Furthermore, whenever an ex-

act ma ximum likelihood e stima te is necessary, we should use these ap-

proxim ations as an initial estimate of the numerical optimization.

When maximization of the log-likelihoo d is necessary but there is

not such an approximation method available, we may red uce the d imen-

sion of the parameter vector to be estimated by n umerical optimization.

In the state-spac e models (9 .1) and (9.2), it is assumed that the dimen-

sion of the time series is ℓ = 1 and the variance of w

is constant with

. Then, if

n|n

n|n−1

, and

R are deﬁned by

n|n−1

, V

n|n

R = 1, (9.24)

then it follows that the Kalman ﬁlters (9.12) and ( 9.13) yield identical

results, even if those param eters are used.

146 ANALY SIS OF TIME SERIES WITH A STATE-SPACE MODEL

In one-step-ahead prediction, it is obvious th at we can obtain ide n-

tical results, even if we replace V

n−1|n−1

and V

n|n−1

n−1|n−1

and

n|n−1

, respectively. In the ﬁltering step, we have

= V

n|n−1

+ R

)

−1

n|n−1

−2

n|n−1

+ 1)

−1

n|n−1

−1

. (9.25)

Assuming th at

R = 1, th e obtained Kalman gain

is iden tical to

. Ther e fore, in the ﬁltering step, we may use

n|n

and

n|n−1

instead of

n|n

and V

n|n−1

. Furthermore, it can be seen that the vectors x

n|n−1

and

n|n

of the state do not change under these modiﬁcations. In summary, if

is time-invariant and R =

is an unknown p arameter, we may apply

the Kalman ﬁlter by setting R = 1. Since we then have d

n|n−1

from (9.18), this yields

ℓ(

) = −

(

N lo g 2

πσ

∑

n=1

log

n|n−1

∑

n=1

−y

n|n−1

)

n|n−1

)

(9.26)

From the likelihood equation

∂

ℓ

∂σ

= −

(

−

(

)

∑

n=1

−y

n|n−1

)

n|n−1

)

= 0, (9.27)

the maximum likelihood estimate of

is obtained by

∑

n=1

−y

n|n−1

)

n|n−1

. (9.28)

Furthermore, denoting the pa rameters in

except for the variance

∗

, by substituting (9.2 8) for (9.26), we have

ℓ(

∗

) = −

(

N log 2

∑

n=1

log

n|n−1

+ N

)

. (9.29)

By th is method, it is possible to reduce the dimension of the param e -

ter vector by one. Su mmarizing the above, the proced ure u sed here is as

follows:

INTERPOLATION OF MISSING OBSERVATIONS 147

1. Apply the Kalman ﬁlter by putting R = 1.

2. Obtain an estimate of the variance

by (9.28).

3. Obtain the log-likelihood ℓ(

∗

) by (9.29).

4. Repeating the above steps (1)–(3), obtain the maximum likeli-

hood estimate

∗

by maximizing the log-likelihood ℓ(

∗

) by

means of numerical o ptimization.

9.7 Interpolation of Missing Observations

In observing time series, a part of the time series might not be able to

be obtained because of unexpected factors, such as the bre akdown of

the observational devices, physical constraints of the observed objects

or the observation systems. In such cases, the actual unobserved data

are called missing observations, or missing values. Even when only a

few percent of the obser vations ar e missing, the length of continuously

observed data that can be used fo r the analysis mig ht become very short.

In such a situation, sometimes we may ﬁll the missing observations with

zeros, the mean value of the tim e series or by linear interpolation. As can

be seen in the numerical example s following, such ad hoc interpolation

for missing o bservations may cause a large bias in the analysis, since it

is equivalent to arbitrarily assuming a particular model.

In this section, we shall explain a method of computing the likelihood

of the time series model and interpolating the missing ob servations using

the state-space model and the Kalman ﬁlter (Jones (1980), Kohn and

Ansley (1986), Kitagawa and G e rsch (1996)). Applying th e state-space

model of time series, it is p ossible to compute an exact likelihood even

when there are missing observations in the data. Thus, we ca n o btain

maximum likelihood estimates of unknown parameters.

Let I(n) be the set of time instances at which the time series was

actually observed. If there are no missing observations, it is obvious that

I(n) = {1,···,n}. The n, for the observations Y

≡{y

|i ∈ I(n)}, the log-

likelihood of the time series is given by

ℓ(

) = log p(Y

)

∑

n∈I(N)

log p(y

n−1

). (9.30)

Since Y

≡Y

n−1

holds when the obser vation y

is missing, as in the

case of increasing horizon prediction, the Kalman ﬁlter algorithm can

be performed by just skipping the ﬁltering step. Namely, the predictive

distribution p(x

n−1

) of the state, or equivalently, the mean x

n|n−1

and

148 ANALY SIS OF TIME SERIES WITH A STATE-SPACE MODEL

the variance-covariance matrix V

n|n−1

, can be obtained by repeating the

prediction step for all n and the ﬁltering step for n such that n ∈ I(N).

Therefore, after computing y

n|n−1

and d

n|n−1

by equation s (9.17) and

(9.18), similarly to the prec e ding section, the log-likelihood of the time

series mode l is deﬁned as

ℓ(

) = −

∑

n∈I(N)



ℓlog 2

+ log|d

n|n−1

+ (y

−y

n|n−1

)

−1

n|n−1

−y

n|n−1

)



. (9.31)

If a tim e series model is already given, th e model can be used for

interpolation of missing observations. Sim ilar to the likelihood com-

putation, ﬁrstly, we obtain the p redictive distributions {x

n|n−1

, V

n|n−1

}

and the ﬁlter distributions {x

n|n

, V

n|n

} using the Kalman ﬁlter and skip-

ping the ﬁltering steps. Then, we can o btain the sm oothed estimates of

the missing observations by applying the ﬁxed-interval smoothing algo-

rithm (9.14). The variance-covariance matrix of the estimate is obtain ed

by d

n|N

= H

n|N

+ R

. Consequently, an estimate of the missing ob-

servation y

is obtained as y

n|N

= H

n|N

Thus, the results of inter polation by op timal models are sig niﬁcantly

different from conventional inter polations, which a re generated by re-

placing missing observations with the me a n or by straight-line interp o-

lation. As can be seen from this example, interpolation o f the missing

observations by a particular algorithm co rresponds to assuming a partic-

ular time series model, different from the true model gen e rating the data.

Therefore, if we perform interpolation without carefully selecting the

model, it may cause signiﬁcant bad effects in the subsequent analysis.