Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

THE PARCOR METHOD 109

relation between the coefﬁcients of the AR model of order m −1 and the

coefﬁcients of the AR model of order m:

= a

m−1

−a

m−1

m−j

. (7.23)

Therefore, if we can estimate the PARCOR a

, the other c oefﬁcients

can be automatically determined by using the above relation. In Levin-

son’s algorith m, we used the following formula for the estimation of

that is obtained by substituting the sample autocovariance functions

,···,

into (B.8) in the Appendix B:

ˆa



−

m−1

∑

j=1

ˆa

m−1



−1



−

m−1

∑

j=1

ˆa

m−1

m−j





m−1



−1



−

m−1

∑

j=1

ˆa

m−1

m−j



. (7.24)

In this section, we present another method of estimating PARCOR

directly from the time series y

,···, y

without using th e sample au-

tocovariance functions. First of all, let w

m−1

denote the pr e diction error

of the backward AR model with order m −1:

m−1

∑

j=1

m−1

n+ j

+ w

m−1

. (7.25)

In the case of univariate time series, since the autocovariance func-

tion is an even function, the AR coefﬁcients of the forward model coin -

cide with those of the backward mo del. Using this property, from Ap-

pendix (B.2), we have the expression

−

m−1

∑

j=1

m−1

m−j

= E



−

m−1

∑

j=1

m−1

n−j



n−m



= E



m−1

n−m



= E



m−1

n−m



. (7.26)

Therefore, the left-hand side of Equation (7.26) can be approximated by

N −m

∑

n=m+1

m−1

n−m

. (7.27)

110 ESTIMATION OF AN AR MODEL

On the other hand, from (B.4), we have

−

m−1

∑

j=1

m−1

= E



n−m

−

m−1

∑

j=1

m−1

n−m+ j



n−m



= E



m−1

n−m



= E



m−1

n−m



. (7.28)

Using the equality E



m−1

n−m



= E



m−1



, various estimates of (7.2 6)

can be obtain e d corresponding to (7.28) a s follows,

N −m

∑

n=m+1



m−1

n−m



(7.29)

N −m



∑

n=m+1



m−1

n−m



∑

n=m+1



m−1





(7.30)

2(N −m)



∑

n=m+1



m−1

n−m



∑

n=m+1



m−1





. (7.31)

Based on these estimates, we obtain the following three estimators

of PARCOR

ˆa

∑

n=m+1

m−1

n−m



∑

n=m+1



m−1

n−m





−1

(7.32)

ˆa

∑

n=m+1

m−1

n−m



∑

n=m+1



m−1

n−m



∑

n=m+1



m−1





−

(7.33)

ˆa

= 2

∑

n=m+1

m−1

n−m



∑

n=m+1



m−1

n−m



∑

n=m+1



m−1





−1

(7.34)

In addition to these estimators, we can deﬁne another estimator that

could be obtained by replacing



m−1

n−m



with



m−1



in (7.32). The

estimate of PARCOR obtained by (7.32) is a regression coefﬁcient when

the prediction error v

m−1

of the forward mode l is regressed on the pre-

diction error w

m−1

n−m

of the backward model. More over, the estima te of

(7.33) corresponds to the deﬁnition of PARCOR, since it is the correla-

tion coefﬁcient o f v

m−1

and w

m−1

n−m

. The estimate of (7.34) minimizes the

mean of the variances of the forward prediction e rrors a nd th e backward

LARGE SAMPLE DISTRIBUTION OF THE ESTIMATES 111

prediction errors, and consequently Burg’s algorithm based on the maxi-

mum entropy method (MEM) is obtained (Burg (1967)). The procedures

to estimate the AR model from the time series y

,···, y

using the PAR-

COR m ethod are described below. Here, for simplicity, the mean value

of the time series y

is assumed to be 0.

1. Set v

= w

= y

, for n = 1,···, N. In add ition, for the AR

model of ord er 0, compute

= N

−1

∑

n=1

, and AIC

N(log 2

+ 1) + 2.

2. For m = 1, ···,M, repeat the following steps (a)–(f).

(a) Estimate the PARCOR ˆa

by any of the formulae (7.32),

(7.33) or (7.34).

(b) Obtain the AR coefﬁcients ˆa

,···, ˆa

m−1

by (7.23).

= v

m−1

− ˆa

m−1

n−m

(d) For n = m + 1,···,N, obtain the backward prediction error

as w

n−m

= w

m−1

n−m

− ˆa

m−1

(e) Estimate the in novation variance of the AR model of order

m by

m−1



1 −( ˆa

)



(f) Obtain AIC by AIC

= N(log 2

+ 1) + 2(m + 1).

7.5 Large Sample Distribution of t he Estimates

On the assumption that th e time series is generated by an AR model of

order m, for large sample size n, the distribution of the estimates of the

AR parameters is app roximately given by

ˆa

∼ N



−1



, (7 .35)

where Σ is the Toepliz matrix (7.2) g enerated fro m the autocovariance

function and

is the innovation variance (Brock w ell and Davis (1991),

Shumway and Stoffer (2000).

On the oth e r hand, if the time series f ollows AR model of order m,

and if j is larger than m, the estimated PARCOR a

, i.e., the j-th au-

toregressive coefﬁcient of the AR model of order j ( j > m), are approxi-

mately distributed independently with varaince 1/n (Q uenouille (1948),

Box and Jenkins (1970), Shumway and Stoffer (2000)), i.e.,

Var

ˆa

≃

for j > m. (7.36)

This pro perty can be used to check the adequacy of the estimated order

112 ESTIMATION OF AN AR MODEL

Table 7.1 Innovation variances and AI C values of the AR models of various

orders ﬁtted to the sunspot number data.

AIC

0 0.22900 317.05 7 0.06694 46.95 14 0.05766 26.45

1 0.09204 108.49 8 0.06573 44.73 15 0.05716 26.47

2 0.07058 49.17

9 0.05984 25.02 16 0.05701 27.84

3 0.06959 47.90 10 0.05829 20.96 17 0.05701 29.84

4 0.06868 46.85 11 0.05793 21.52 18 0.05669 30.53

5 0.06815 47.08

12 0.05780 23.02 19 0.05661 32.21

6 0.06805 48.72 13 0.05766 24.47 20 0.05615 32.32

of the model. The relation between AIC and the estimated PARCOR is

considered in Problem 1 of this Chapter.

Example (AR modeling for sunspot number data) Table 7 .1 sum-

marizes the results of ﬁtting AR mo dels of orders up to 2 0 by the Yule-

Walker method to the logarithm of the sunspot number data shown in

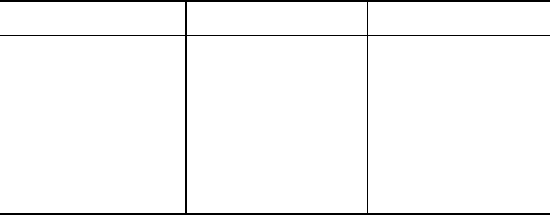
Figure 1.1(b) . Figure 7.1(a) shows the estimated PARCORs for orders

1,.. .,20. From Figure 7.1( b) that shows the ch ange in AIC values as m

varies, it can be seen that AIC is minimized at m = 10, and for larger m

it gradually increases.

Since the sample size of the sunspot number data is n = 231, f rom

(7.36), the large sample standard error of the estimated PARCOR is

(231)

−1/2

≃ 0.066. It can be seen that the PARCORs for m = 11,. . . ,16

are very small compare d with this standara d error that supports the order

selected by AIC.

On the other hand, plot (c) shows the spectrum obtained by the AR

model of order m = 10 that min imizes the AIC. A strong peak is seen

in the vicinity of the frequency f = 0.1, corresponding to a cycle of

approximately 10 years.

Example (AR modeling and power spectr a estimated through AR

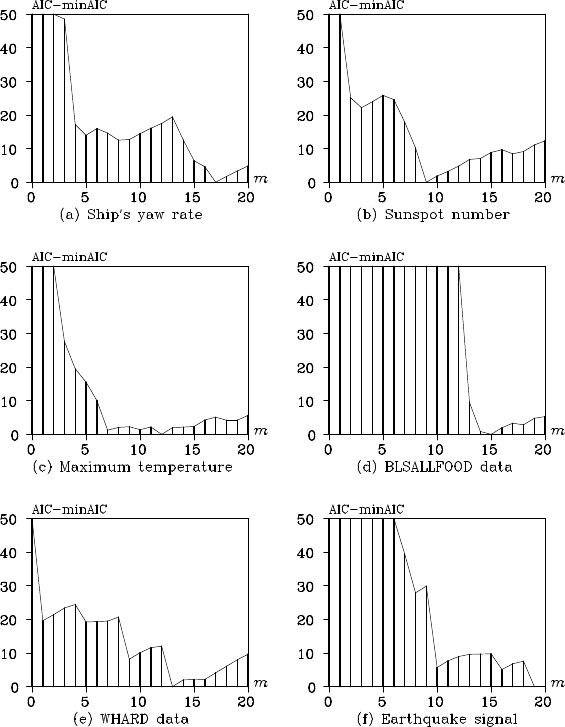
models) Figure 7 .2 (a)–(f) shows the changes of AIC, when AR mod-

els with orders 1 to 20 are ﬁtted to the time series shown in Figure 1.1

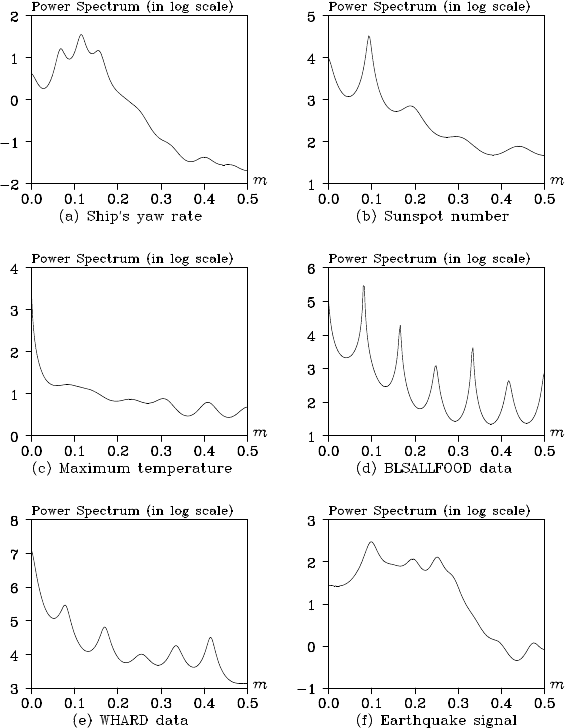
(a)–(f) by the Yule-Walker method. Figure 7.3 shows the power spectr a

of the tim e series obtained by the method presented in Chapter 6 using

the AIC best AR model among the orders up to 20.

THE YULE-WALK ER METHOD FOR MAR MODEL 113

Figure 7.1 Changes of PARCOR and AIC and estimated spectrum by the AIC

best AR model for t he sunspot number data.

7.6 Estimation of a Multivariate AR Model by the Yule-Walker

Method

In this section, estimation methods for multivariate AR models are

shown. Here inafter k denotes the number of variables (or dimensio ns) of

a multivariate time series. The parameter s of the multivariate AR model

of order m

∑

i=1

n−i

+ v

, v

∼ N(0,V

), (7.37)

are the variance-covariance matr ix V

of the innovation v

and the AR

coefﬁcient matrices A

,···, A

(Akaike and Nakagawa (1989)).

When a multivariate AR model is given, the cross-covariance f unc-

tion is obtained from (6.28) and (6.29). On the other hand, using these

equations, the estimate s of the p a rameters of the multivariate AR model

can be obtained through the sample cross-covariance function. For actual

computation, similarly to the univariate AR model, they can be deter-

114 ESTIMATION OF AN AR MODEL

Figure 7.2: Change in AIC values, as the order varies.

THE YULE-WALK ER METHOD FOR MAR MODEL 115

Figure 7.3: Estimated spectra by AR models with minimum AIC orders.

116 ESTIMATION OF AN AR MODEL

mined efﬁciently by the following algorithms. However, for a multivari-

ate time series, the backward mod e l is different from the forward model.

In the case of a univariate time series, the forward AR mode l coincides

with the backward A R model, b ecause the autocovariance func tion is an

even function. But th is property is not satisﬁed by multivariate time se-

ries. Therefore, in order to derive an efﬁcient algorithm similar to Levin-

son’s algorithm , in a ddition to (7.37), we have to consider the b a ckward

multivariate AR model

∑

i=1

n+i

+ u

, u

∼ N(0,U

), (7.38)

and we need to estimate the variance-covariance matrix U

and the co-

efﬁcients B

, as well as A

and V

, simultaneously (Whittle (1963)).

1. Set

= C

and compute the AIC of the AR model of

order 0 as

AIC

= N(k log 2

+ log|

|+ k) + k(k + 1).

2. For m = 1, ···,M, repeat the following steps (a)–(e).

(a) W

= C

−

∑

m−1

i=1

m−1

m−i

(b) Obtain the PARCOR matrices of the fo rward and backward

AR models by A

= W

−1

m−1

and B

= W

−1

m−1

AR models by A

= A

m−1

−A

m−1

m−i

and B

= B

m−1

−

m−1

m−i

for i = 1,...,m −1.

(d) Compute the innovation variance-covariance m atrices by

= C

−

∑

i=1

and U

= C

−

∑

i=1

(e) Compu te the AIC value of the AR model of order m by

AIC

= N(k log 2

+ log|

|+ k) + k(k + 1) + 2k

By the above-mentioned algorithm, we compute AIC

,···, AIC

and select the m that results in the minimum AIC value as the best order

of the mu ltivariate AR mode l. In this method, it is assumed that the au-

toregressive coefﬁcients a

(i, j ) have common orders for all i and j.

Example Table 7.2 shows the results of ﬁtting thr ee-variate AR mo d-

els of orders up to 20 by the Yule-Walker method for the ship’s data

shown in Figure 1.1. The AIC is minimized at m = 10, and increases

gradua lly afterward. The power spectra, the cross spectra, the coherency,

and th e noise contribution, etc., that are shown in Chapter 6 are obtained

from the multivariate AR mo del of ord e r m =10 , which attains the min-

imum AIC value.

LEAST SQUARES METHOD FOR MAR MODEL 117

Table 7.2: AICs of mult ivariate AR models ﬁtted to ship’s data.

m AIC

0 7091.71 7 5105.83 14 510 0.98

1 6238.80

8 5096.35 15 5113.05

2 5275.36 9 5087.91 16 511 6.52

3 5173.02 10 5083.79 17 512 9.42

4 5135.20

11 5093.79 18 5136.06

5 5136.63 12 5091.42 19 514 3.56

6 5121.02 13 5097.98 20 515 7.37

7.7 Estimation of a Multivariate AR Model by the Least Squares

Method

To obtain the least squares estimates of the parameters of a m ultivariate

AR m odel by the Householder method, w e ﬁrst transform the model

(7.37) to the fo llowing expression with instan ta neous response:

= B

∑

i=1

n−i

+ w

, w

∼ N(0,W ). (7.39)

(Ta kanami and Kitagawa (1991), Kitagawa and Gersch (1996)). Here,

is a lower triangular matrix whose components on and above the di-

agonal are zero, thus







0 0 ··· 0

(2,1) 0 ··· 0

(k,1 ) ··· b

(k,k −1) 0







. (7.40)

The variance-covariance matrix W is assumed to be a diagonal ma trix

W =







0 ··· 0







. (7.41)

Since the model (7.39) can be expressed as

= (I −B

)

−1

∑

i=1

n−i

+ (I −B

)

−1

, (7.42)

118 ESTIMATION OF AN AR MODEL

by putting

= (I −B

)

−1

V = (I −B

)

−1

W (I −B

)

−T

, (7. 43)

there is a one-to-one correspondence be tween the multivariate AR model

(7.38) and the mu ltivariate model with instantaneo us response given in

(7.39). Therefore, if the coefﬁcient matrices B

,···, B

and the vari-

ances

,···,

of the model (7.39 ) are estimated , the multivariate AR

model will also be o btained by (7.43).

The advantage of this method is that we do not need to estimate all

of the coefﬁcients simultaneo usly, since the variance-covariance m a trix

W is a diagonal matrix. Na mely, if we denote the coefﬁcient matrix B







(1,1) ··· b

(1,k )

(k,1 ) ··· b

(k,k)







, (7.44)

the coefﬁcients of the k models, that is, {b

(p,q ), i = 1, ···,m, q =

1,···, k,

} for p = 1, ···,k can b e estimated indepen dently.

This method is far more computation a lly efﬁcient than the method

that estimates all of the coefﬁcients at once. To realize the above estima-

tion by the Householder method, ﬁrstly w e construct an (N −m)×(km +

k) matrix

X =







··· y

m+1

··· y

m+2

N−1

··· y

N−m







, (7.45)

and transform it to an upper triangular matrix by the Householder trans-

formation,

S =







··· s

1,km+k

km+k,km+k







. (7.46)

It should be note d here that the (km + 1) ×(km + 1) upper-left sub-

matrix has all the necessary infor mation to estimate the following mode l

for the ﬁrst component:

(1) =

∑

i=1

(1,1)y

n−i

(1) + ···+

∑

i=1

(1,k )y

n−i

(k) + w

. (7.47)