Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

THE POWER SPECTRUM OF THE ARMA PROCESS 89

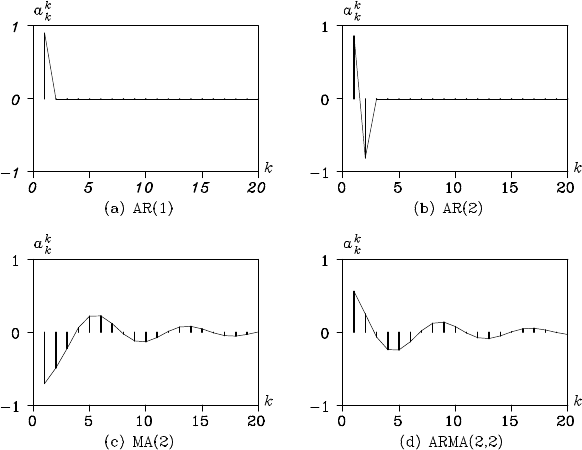
Figure 6.3: PARC ORs of the four models.

∞

∑

k=−∞



∞

∑

j=0

n−j



∞

∑

p=0

n−k−p



−2

ik f

∞

∑

k=−∞

∞

∑

j=0

∞

∑

p=0



n−j

n−k−p



−2

ik f

Here, using g

= 0 for p < 0, from (6.2), the power sp ectrum is ex-

pressed as

p( f ) =

∞

∑

k=−∞

∞

∑

j=0

j−k

−2

ik f

∞

∑

j=0

∑

k=−∞

−2

i j f

j−k

−2

i(k−j) f

∞

∑

j=0

∞

∑

p=0

−2

i j f

ip f



∞

∑

j=0

−2

i j f



, (6.18)

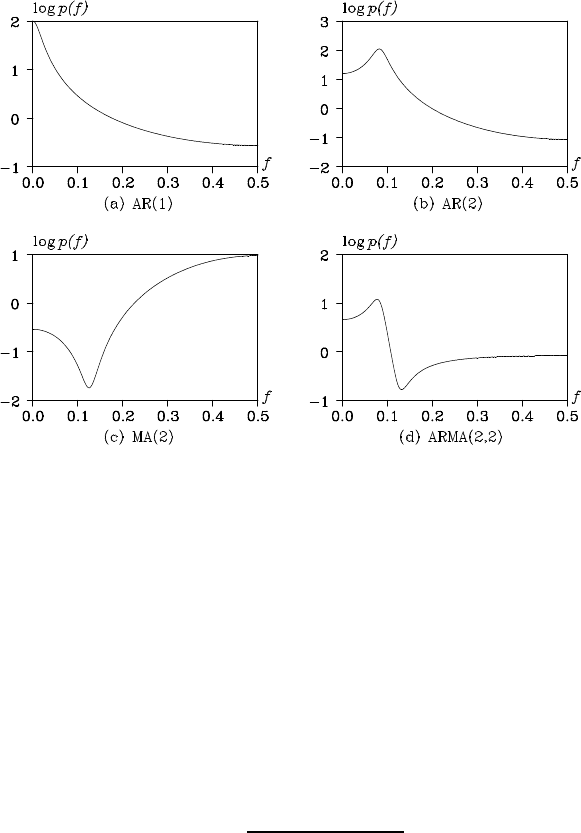
90 ANALYSIS OF TIME SERIES USING ARMA MODELS

Figure 6.4: Logarithm of the power spectra of the four models.

where

∑

∞

j=0

−2

i j f

is the Fourier transform of the impulse response

function and is called the frequency response function. On the other hand,

putting B = e

−2

i f

in (6. 7), it can b e expressed as

∞

∑

j=0

−2

i j f



1 −

∑

j=1

−2

i j f



−1



1 −

ℓ

∑

j=1

−2

i j f



. (6.19)

Therefore, substituting the above frequency response function in to

(6.18), the power spectrum of the ARMA model is given b y

p( f ) =



1 −

ℓ

∑

j=1

−2

i j f



1 −

∑

j=1

−2

i j f



. (6.20)

Example. Figure 6.4 shows the logarithm of the power spe ctra of

the four models. The power sp ectrum of the AR model with or der one

THE POWER SPECTRUM OF THE ARMA PROCESS 91

Figure 6.5: Line-like spectrum of ARMA(2.2).

does not have any peak or trough. A peak is seen in the plot (b) of the

spectrum of the seco nd order AR model and one trough is seen in the

plot (c) of the second order MA model. On the other hand, the spectrum

of the ARMA model of order (2.2) shown in the plot (d) has both one

peak and one tro ugh.

These examples indicate that there must be close relations between

the AR and MA orders and the nu mber of pe aks and troughs in the spec-

tra. The logarithm of the spectrum, log p( f ) shown in Figur e 6.4, is ex-

pressible as

log p( f ) = log

−2 log



1 −

∑

j=1

−2

i j f



+ 2 log



1 −

ℓ

∑

j=1

−2

i j f



(6.21)

Therefore, the peak and the trough of the spectrum appear at the

local minimum of |1 −

∑

j=1

−2

i j f

| and at the local minim um of

|1 −

∑

j=1

−2

i j f

|, respectively. The number of pea ks and troughs, re-

spectively, correspond to the number of roo ts of th e AR operato r a nd the

MA operator as will be explained in the next subsection. To express k

peaks or k troughs, the AR order or the MA order must be hig her than

or equa l to 2k, respectively. Moreover, the lo cations and the heights of

the peaks o r the troughs are determined by the angles and the absolute

values of the complex roots of the characteristic equation.

In particular, when the angles of the complex roots of the AR oper a-

tor coincide with th ose of the MA operator, a line spectrum appears. For

example, if the AR and MA co efﬁcients of the ARMA (2.2) model are

given by

m = 2 , a

= 0.99

√

2, a

= −0.99

ℓ = 2, b

= 0.95

√

2, b

= −0.95

92 ANALYSIS OF TIME SERIES USING ARMA MODELS

both characteristic equations have roots at f = 0.125 ( = 45 degrees), and

log p( f ) has a lin e-like spectral peak a s shown in Figure 6.5.

6.6 The Charac teristic Equation

The characteristics of an ARMA model are determined by the roots of

the following two polynomial equations:

a(B) = 1 −

∑

j=1

= 0 (6.22)

b(B) = 1 −

ℓ

∑

j=1

= 0. (6.23)

Equations (6. 22) and (6.23) are called the characteristic equation associ-

ated with the AR operator, and th e MA operator, respectively. The roots

of these equations are c alled the characteristic roots. If the roots of the

characteristic equation a(B) = 0 of the AR operator all lie outside the

unit circle, the inﬂuen c e o f noise turbulence at a certain time decays as

time progresses, and then the ARMA model becomes stationary.

On the other hand, if all ro ots of the characteristic equatio n b(B) = 0

of the M A operator lie outside the un it circle, the coefﬁcient of h

b(B)

−1

∑

∞

i=0

converges and the ARMA model can be expressed

by an AR model of in ﬁnite order as

= −

∞

∑

i=1

n−i

+ v

. (6.24)

In this case, the time series is called invertible.

As mentioned in the previous section, the positions of the roots of the

two chara cteristic polynomials have a close relation to the shape of the

spectrum. The peak of the spectrum (or troug h) appears at f =

, if

the complex root of AR (or MA) o perator is expressed in the form

z =

+ i

= re

. (6.25)

Further, the closer th e root r appr oaches to 1, the sharper the peak

and trough of the spectrum become. Figure 6.6 shows th e position s of

the characteristic roots of the four models that have been used for the

examples in this ch apter. The symbols ∗and + den ote the roots of the AR

operator a nd the r oots of the MA operator, respectively. For convenience

in illustration, the position of z

−1

= r

−1

−i

is displayed in Figure 6.6

instead of z.

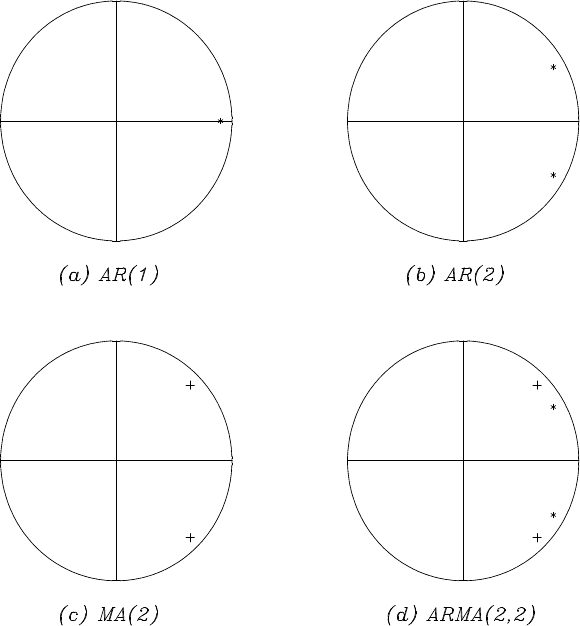
THE MULTIVARIATE AR MODEL 93

Figure 6.6 Characteristic roots. (a) AR model of order 1, (b) AR model of order

2, (c) MA model with order 2 and (d) ARMA model with order (2,2).

6.7 The Multivariate AR Model

For multivariate time series, y

= (y

(1),···, y

(ℓ))

, similar to the case

of univariate time series, the model that expresses a present value of the

time series as a linear combination of pa st values y

n−1

,···, y

n−M

and

white noise is called a multivariate autoregressive mod e l (MAR model)

∑

m=1

n−m

+ v

, (6.26)

94 ANALYSIS OF TIME SERIES USING ARMA MODELS

where A

is the autoregressive coefﬁcient matrix who se (i, j)-th element

is given by a

(i, j ), and v

is an ℓ dimensional white noise that satisﬁes

E(v

) =













, E(v

) =







···

1ℓ

ℓ1

···

ℓℓ







= W

E(v

) = O, for n 6= m (6.27)

E(v

) = O, for n > m.

Here, O denotes the ℓ ×ℓ matrix with 0 eleme nts, a nd W is an ℓ ×ℓ

symmetric matrix satisfying

i j

. The cross-covariance function of

(i) and y

( j) is deﬁned by C

(i, j ) = E



(i)y

n−k

( j)



. Then, the ℓ ×ℓ

matrix C

= E(y

n−k

), the (i, j)-th component of which is C

(i, j ), is

called the cross-covariance function. Similar to the case of the univariate

time series, for the multivariate AR model, C

satisﬁes the Yule-Walker

equation

∑

j=1

−j

+W (6.28)

∑

j=1

k−j

(k = 1,2,···). (6.2 9)

As noted in Chapter 2, the cross-covariance function is not symmetr ic .

Therefore, for multivariate time series, the Yule-Walker equations for the

the backward AR model and the forward AR model are different.

The Fourier transform of the cross-covariance function C

(s, j) is

called the cross spectral density function

s j

( f ) =

∞

∑

k=−∞

(s, j)e

−2

ik f

∞

∑

k=−∞

(s, j) cos(2

k f ) −i

∞

∑

k=−∞

(s, j) sin(2

k f ).

(6.30)

Since the cross-covariance function is not an even function, the cross-

spectrum g iven by (6.30) has an imaginary part and is a complex number.

If the ℓ ×ℓ matrix P( f ) is deﬁned by

P( f ) =







( f ) ··· p

1ℓ

( f )

ℓ1

( f ) ··· p

ℓℓ

( f )







, (6. 31)

THE MULTIVARIATE AR MODEL 95

then the relation s betwe e n the cross-spectrum matrix P( f ) an d the cross-

covariance matrix C

are given by

P( f ) =

∞

∑

k=−∞

−2

ik f

(6.32)

−

P( f )e

ik f

df . (6.33)

For time ser ie s tha t follow the multivariate AR mo del, the cross-

spectrum can be obtained b y (Whittle (1963))

P( f ) = A( f )

−1

W (A( f )

−1

)

∗

, (6. 34)

where A

∗

denotes the complex conjugate of the matrix A, and A ( f ) de-

notes the ℓ ×ℓ matrix whose ( j, k)-th component is deﬁned by

( f ) =

∑

m=0

( j,k )e

−2

im f

. (6.35)

Here, it is assumed that a

( j, j) = −1 and a

( j,k ) = 0 fo r j 6= k. Given

a freque ncy f , the cross spectrum is a complex n umber and can be ex-

pressed as

( f ) =

( f )e

( f )

, (6.36)

where

( f ) =

(ℜ{p

( f )})

+ (ℑ{p

( f )})

( f ) = arctan



ℑ{p

( f )}

ℜ{p

( f )}



ℜ and ℑ denote the real and imaginary parts of the complex number,

respectively. Then,

( f ) is called th e amplitude spectrum and

( f )

is the phase spectrum. Moreover,

coh

( f ) =

( f )

j j

( f )p

( f )

(6.37)

denotes the square of the correlation coefﬁcient be tween frequency com-

ponen ts of time series y

( j) and y

(k) at frequency f and is called the

coherency.

For convenience, A( f )

−1

will be denoted as B( f ) =



( f )



in the

96 ANALYSIS OF TIME SERIES USING ARMA MODELS

following. If the components of the white noise v

are mutually uncor-

related and the variance-covariance matrix becomes the diagonal matrix

W = diag{

,···,

ℓ

}, then the power spectrum of the i-th component

of the time series can b e expressed as

( f ) =

ℓ

∑

j=1

i j

( f )

i j

( f )

∗

≡

ℓ

∑

j=1

i j

( f )|

. (6.38)

This indicates that the power of the ﬂuctuation of the c omponent

i at frequency f can be decomposed into the effects of ℓ noises, i.e.,

i j

( f )|

. Ther efore, if we deﬁne r

i j

( f ) by

i j

( f ) =

i j

( f )|

( f )

, (6.39)

it represents th e ratio of the effect of v

( j) in the ﬂu ctuation of y

(i) at

frequency f .

The r

i j

( f ) is called the relative power contribution, which is app li-

cable to the analy sis of a feedback system (Akaike (1968), Akaike and

Nakagawa (1989)). However, for convenience in drawing ﬁgures, a cu-

mulative power contribution is an effective tool, which is deﬁned by

i j

( f ) =

∑

k=1

( f ) =

∑

k=1

( f )|

( f )

. (6.40)

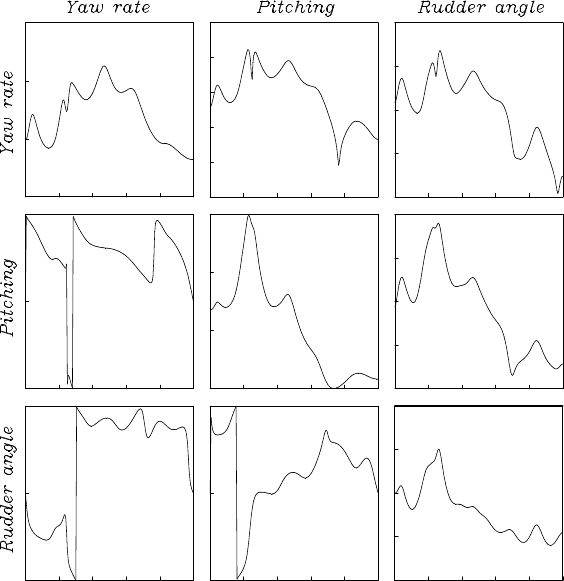
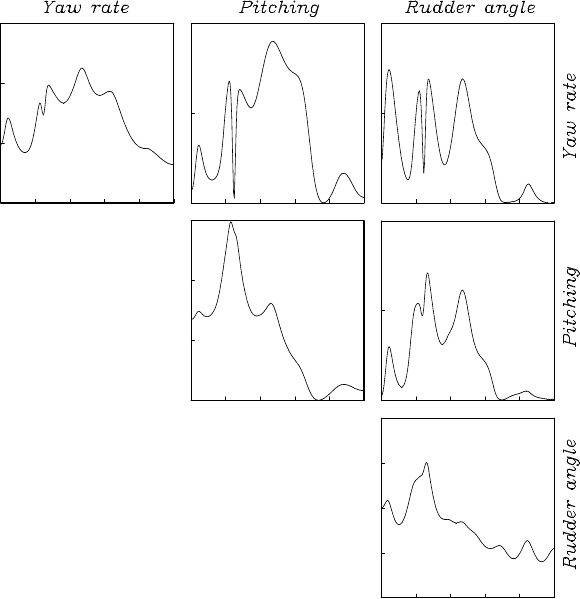
Example Figure 6.7 shows the cross spectra obtained by using a

three-variate AR model for the three- variate time series composed of

the yaw rate, the pitch rate and the rudder angle shown in (a) and (h) of

Figure 1.1 (N = 500 and △t = 2 second) that were originally sampled

every second. T hree of nine plots on the d iagonal in the ﬁgu re show the

logarithm of the power spectra of the yaw rate, the pitch rate and the

rudder angle, respectively. As for the power spectra of the yaw rate, the

maximum peak is seen in the vicinity of f = 0.25 (8 seconds cycle) and

for the pitch rate and the rudder an gle in the vic inity of f = 0.125 (16

seconds cycle). On the other hand, three plots above the diagonal show

the absolute values of the amplitude spectra of the cross spectra, that is,

the logarithm of the amplitude spectra and three plots below the diagonal

show the phase spectra where some discontinuous jumps are seen. The

reason for this is that the phase spectra are displayed with in the range

[−

THE MULTIVARIATE AR MODEL 97

Figure 6.7 Spectra (diagonal), amplitude spectra (above diagonal) and phase

spectra ( below diagonal) for t he ship data.

Figure 6.8 shows the power spectra and the coherencies. Three p lots

on the diagonal show the power spectra similarly to Figure 6.7. Three

other plots above the diagonal show the coherencies. Yaw rate and pitch-

ing both have two sig niﬁcant peaks at the same frequencies. Th e peak

of the rudder angle has slightly smaller frequency than those of yaw rate

and pitching.

On the other hand, Figure 6.9 shows the power contributions. In Fig-

ure 6.9, the two plots on top, respectively, show the a bsolute and the

relative power c ontributions of th e yaw rate. Here, the plots in the left

column show the absolute cumulative power co ntribution and the plots

in the right column show th e cumulative relative power contribution. All

plots in both columns of Figure 6.9 show the contribution of the yaw rate,

98 ANALYSIS OF TIME SERIES USING ARMA MODELS

Figure 6.8: Power spectra (3 in diagonal) and coherencies.

the pitch rate and th e rudder angle f rom the bottom to the top in each

plot, respectively. The inﬂuen c e of the rudder angle is clearly visible for

f < 0.13. However, the inﬂuence of the rudder angle is barely noticeable

in the vicinity of f = 0.14 a nd 0.23, where the dominant power of the

yaw rate is found. This is probably explained by noting that this data set

has been observed under the control of a conventional PID autopilot sys-

tem that is designed to suppress the power of variation in the frequ e ncy

area f < 0.13.

Two plots in the seco nd row show the power contribution of the

pitching. The contribution of the rudder angle is almost 50 percent in the

vicinity of f = 0.1, where the power spectrum is strong. This is thought

to be a side effect of the steering to suppress the variation of the yaw