Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

THE MULTIVARIATE AR MODEL 99

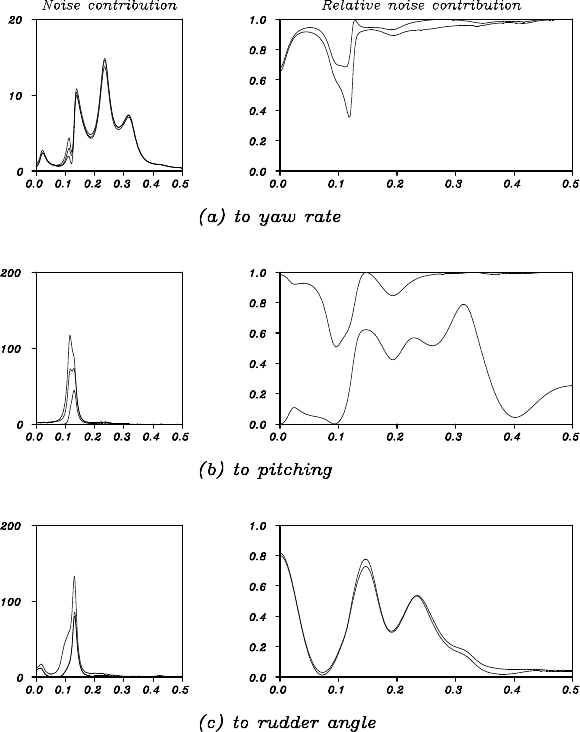
Figure 6.9: Power contributions.

rate. On the other hand, actual power is very small for f > 0.14 thou gh

a strong inﬂuence of the yaw rate is seen.

Two ﬁg ures in the third row show the power contribution to the rud-

der angle. It can be seen that the inﬂuence of the yaw rate is extreme ly

strong in the vicinity of f = 0.12, wher e the m ain power is located.

100 ANALYSIS OF TIME SERIES USING ARMA MODELS

Moreover, it can also be seen that, in the range of f < 0.08 , the con-

tribution of the yaw rate becomes greater as the freq uency decreases.

Problems

1.(1) Show the stationa rity condition for AR(1).

(2) Show the stationarity condition for AR(2).

2. For an AR(1), y

= ay

n−1

+ v

, v

∼ N(0,

(1) Obtain the one-step-ahead prediction e rror variance.

(2) Obtain the two-step-ahea d prediction error variance.

(3) Obtain the k-step-ahead prediction error variance.

3. Assuming that the time series follows the models shown below and

that v

follows a white noise with mean 0 and variance

, obtain the

autocovariance function C

(1) AR model of order 1: y

= −0.9y

n−1

+ v

(2) AR model of order 2: y

= 1.2y

n−1

−0.6y

n−2

+ v

(3) MA model of order 1: y

= v

−bv

n−1

(4) ARMA mode l of order (1,1): y

= ay

n−1

+ v

−bv

n−1

4. Assume that a time series follows an AR model of order 1, y

n−1

+ v

, v

∼ N(0,1).

(1) When the noise term v

is not a white noise but follows an autore-

gressive process of order 1, v

= bv

n−1

+ w

, show that y

follows

an AR mode l of order 2.

(2) Obtain the autocovariance functio n C

, k = 0,1,2, 3 of the contam-

inated series x

, deﬁned by x

= y

+ w

∼ N(0,0.1 ).

5.(1) Using the result of Problem 3 for Chap ter 3 and the deﬁnition of

the power spectrum, show that the power spectru m of MA model

with order 1 can be expressed as p( f ) = |1 −be

−2

i f

, where the

right-ha nd side can be expressed as 1 + b

−2bcos(2

f ).

(2) Using the fact that if

= 1, the spectrum of an AR model of o rder

1, y

= ay

n−1

, can be expressed as p( f ) = (1 −2a cos(2

f )+

)

−1

, and show that the maximum and the minimum of the spec-

trum occurs at f = 0 or f = 0.5. Also, consider where the spectrum

p( f ) attains its maximum .

6. For an AR model of order 2, y

= a

n−1

+ a

n−2

+ v

, v

∼

N(0,

THE MULTIVARIATE AR MODEL 101

(1) Show the form ula to obtain the autocovariance function C

,.. . .

(2) Show the expression to obtain the power spectrum p( f ), 0 ≤ f ≤

1/2.

(3) Obtain C

, C

when a

= 0.8, a

= −0.6 and

= 1.

(4) For the same case, obtain the expression for the power sp e ctrum

p( f ). Investigate for which fre quency f , p( f ) attains its maxi-

mum.

7. Assume that a time series y

follows an MA m odel of order 1; y

−bv

n−1

, v

∼ N(0,1).

(1) Obtain the autocovariance function C

, k = 0,1,2, 3.

(2) Express the time series by an AR model.

8.(1) Obtain the variance of the k-step -ahead prediction error

n+k|n

for

an MA model of order 1; y

= v

−bv

n−1

, v

∼ N(0,1).

(2) Express an AR model o f order 1, y

= ay

n−1

+ v

, using an MA

model of inﬁnite order and ob tain the variance of the k-step-ah ead

prediction error variance.

(3) Using the formal expansion of the rand om walk model y

= y

n−1

, obtain the MA model of inﬁnite order. Using that expression,

obtain the k-step-ahead prediction error variance of the random

walk model.

Chapter 7

Estimation of an AR Model

Among the stationary time series models discussed in th e pr eceding

chapter, very efﬁcient estimation methods can be derived f or AR mod-

els. This chapter presents methods for estimating the parameters of the

AR model by the Yule-Walker method, the least squares method and the

PARCOR method. A meth od of determining the order of the AR model

using the AIC is also shown. In addition, the Yule-Walker method and

the least squares me thod for parameter estimation of the multivariate AR

model are shown.

7.1 Fitting an AR Model

Assuming that a time series y

,···, y

is given, we consider the problem

of ﬁtting an autoregressive model (AR model)

∑

i=1

n−i

+ v

, (7.1)

where m denotes the order of the autoregression, a

is the autoregre ssive

coefﬁcient and v

is w hite noise that follows a norma l distribution with

mean 0 and variance

(Akaike (1969), Box and Jenkin s (1970), Akaike

and Nakagawa (1989), Brockwell and Davis (1991)).

is sometimes

called the innovation variance.

To ide ntify an AR model, it is necessary to determine the order m

and estimate the autoregressive coefﬁcients a

,···, a

and the variance

based on the data. In the following, these parameters will be denoted

= (a

,···, a

)

Under the assumption that the order m is given, consider the estima-

tion of the parameter

by the m a ximum likelihood method. The joint

distribution of tim e series y = (y

,···, y

)

, following the AR model, be-

comes a multivariate norma l distribution. When the model (7.1) is given,

the mean vector of the auto regressive pr ocess y is 0 and the variance-

103

104 ESTIMATION OF AN AR MODEL

covariance matrix is given by

Σ =







··· C

N−1

··· C

N−2

N−1

N−2

··· C







, (7. 2)

where the autocovariance function C

is deﬁned by (6.12). Therefore, the

likelihood of the AR model is obtained by

) = p(y

,···, y

)

= (2

)

−

|Σ|

−

exp



−

−1



. (7. 3)

However, when the number N o f data is large, the computation of the

likelihood by this method becomes difﬁcult because it involves the inver-

sion and computation of the determinant of the N ×N matrix Σ. To obtain

the maximum likelihood estimate of

that max imizes (7.3), it is neces-

sary to apply a numerical optimization method, since the likelihoo d is a

complicated function of the parameter

. In general, however, the likeli-

hood of a time ser ies model can be efﬁciently calculated by expressing

it as a product of conditional distributions

) = p(y

,···, y

)

= p(y

,···, y

N−1

)p(y

,···, y

N−1

)

∏

n=1

p(y

,···, y

n−1

). (7.4)

Using a Kalman ﬁlter, each term in the right hand side of (7.4) can be

efﬁciently and exactly evaluated, which makes it possible to compute the

exact likelihood of the ARMA model and other time series models. Such

a method will be treated in Chapter 9. When the maximum likelihood

estimate

of the AR model has been obtained, the AIC for the m odel is

deﬁned by

AIC = −2 (maximum log-likelihood)+ 2 (number of parameters)

= −2 log L(

) + 2(m + 1). (7.5)

To select the AR order m by the minimum AIC method, we calculate

the AICs of the AR models with orders up to M, that is, AIC

,···, AIC

and select the ord e r that results in the minimum AIC value (Akaike

(1973, 1974 ), Sakamoto et al. (1986), Konishi and Kitagawa (2008)).

YULE-WALKER METHOD AND L EVINSON’S ALGORITHM 105

7.2 Yule-Walker Method and Levinson’s Algorithm

As shown in Chapter 6, the autocovariance function of the AR model

(7.1) of order m satisﬁes the Yule-Walker equation (Akaike (1 969), Box

and Jenkins (197 0))

∑

i=1

(7.6)

∑

i=1

j−i

. (7.7)

On the other hand, once the time series has been o btained, by com-

puting the sample autocovariance functions

and substituting them into

(7.7), we obtain a system of linear equations for th e unknown autoregres-

sive coefﬁcients a

,···, a







···

m−1

···

m−2

m−1

m−2

···































. (7.8)

By solving this equation, the estimates ˆa

of the AR coefﬁcients are ob-

tained. Then, from (7.6), an estimate of the variance

is obtained by

−

∑

i=1

ˆa

. (7.9)

The estimates ˆa

,···, ˆa

, and

obtained by this method are called

the Yule-Walker estimates. Since the variance of the predictio n errors of

the AR model with coefﬁcients a

is given by





= E



−

∑

i=1

n−i



= C

−2

∑

i=1

∑

i=1

∑

j=1

i−j

, (7.10)

we obtain equa tion (7.7 ) from

∂

E(v

)

∂

= −2C

+ 2

∑

j=1

i−j

= 0. (7.11)

106 ESTIMATION OF AN AR MODEL

Therefore, we can consider that the Yule-Walker estimates ob tained

by solving (7.8) after substituting

for C

in (7.11 ) approximately min-

imize the variance of prediction errors. To obtain the Yule-Walker esti-

mates for a n AR model of order m, it is necessary to solve a system of

linear equations with m unknowns. In a ddition, to select the order of the

AR mod el by the minimum AIC method, we need to evaluate the AIC

values of the models with orders up to M, the maximum order. Namely,

we have to estimate the coefﬁcients by solving systems of linear equa-

tions with one unknown, ... , M unk nowns.

However, with Levinson’s algorithm, the se solutions can be obtained

quite efﬁciently. Hereina fter, the AR coefﬁcients and the innovation vari-

ance of the AR model of order m are denoted as a

and

, respectively.

Then Levinson’s algorithm is deﬁned as fo llows:

1. Set

and AIC

= N(log 2

+ 1) + 2

2. For m = 1, ···,M, repeat the following steps

(a) ˆa



−

m−1

∑

j=1

ˆa

m−1

m−j





m−1



−1

(b) ˆa

= ˆa

m−1

− ˆa

ˆa

m−1

m−i

for i = 1,...,m −1,

(c)

m−1

{1 −( ˆa

)

(d) AIC

= N(log 2

+ 1) + 2 (m + 1).

In Levinson’s algo rithm, the PARCOR ˆa

introdu ced in Chapter 6

plays an impo rtant role. This algorithm will be explained in detail later

in Appendix B.

7.3 Estimation of an AR Model by the Least Squares Method

In this section , the least square s method explained in Ch a pter 5 will be

applied to the estimation of the AR model. Putting

= (a

,···, a

)

from (7.4) , the log-likelihood of the AR mo del becomes

ℓ(

) =

∑

n=1

log p(y

,···, y

n−1

). (7.12)

Here, for the AR mod el of order m, since the distribution of y

is spec-

iﬁed by the values of y

n−1

,···, y

n−m

for n > m, each term in (7.12) is

given by

p(y

,···, y

n−1

) = p(y

n−m

,···, y

n−1

)

THE LEAST SQUARES METHOD 107

= −

√

πσ

exp



−



−

∑

i=1

n−i





log p(y

,···, y

n−1

) = −

log 2

πσ

−



−

∑

i=1

n−i



(7.13)

Therefore, by ignoring the initial M (M ≥ m) terms of (7.12), the log-

likelihood of the AR model is obtained a s

ℓ(

) = −

N −M

log 2

πσ

−

∑

n=M+1



−

∑

i=1

n−i



(7.14)

(Kitagawa and Akaike (1978), Saka moto et al. (1986), Kitagawa and

Gersch (1996)).

Similar to th e case of the regression model, for arbitrarily given au-

toregressive coefﬁcients a

,···, a

, the max imum likelihood estimate of

the variance

maximizing (7.14) satisﬁes

∂

ℓ(

)

∂σ

= −

N −M

)

∑

n=M+1



−

∑

i=1

n−i



= 0, (7.15)

and is obtained as

N −M

∑

n=M+1



−

∑

i=1

n−i



. (7.16)

Substituting this into (7.14), the log-likelihood beco mes a function

of the autoregre ssive c oefﬁcients a

,···, a

ℓ(a

,···, a

) = −

N −M

log 2

−

N −M

. (7.17)

Here, since the logarithm is a monotone in creasing function, maximiza-

tion of the approximate log-likelihood (7.17) can be achieved by mini-

mizing the variance

. This means that the approximate maximum like-

lihood estimates of the AR model can be obtained by the least squares

method. To obtain the least squares estimates of the AR models with or-

ders up to M by the Householder transformation discussed in Chapte r 5,

deﬁne the matrix Z and the vector y by

Z =







M−1

··· y

M+1

··· y

N−1

N−2

··· y

N−M







, y =







M+1

M+2







. (7.18)

108 ESTIMATION OF AN AR MODEL

For actual computatio n, construc t the (N −M) ×(M + 1) matrix

X = [ Z | y ] =







··· y

M+1

··· y

M+2

N−1

··· y

N−M







, (7.19)

and transform it to an upper triangular matrix

HX =











··· s

1,M+1

M,M+1

M+1,M+1







, (7.20)

by Householder transformation.

Then, for 0 ≤ j ≤M, the innovation variance and the AIC of the AR

model of order j are obtained by

N −M

M+1

∑

i= j+1

i,M+1

AIC

= (N −M)(log 2

+ 1) + 2( j + 1). (7.21)

Moreover, the least squares estimates of the autoregressive coefﬁcients

that are the solutions of the linear equations







··· s

1 j

j j

























1,M+1

j,M+1







, (7.22)

can be easily obtained by backward substitution a s follows:

ˆa

j,M+1

j j

ˆa

i,M+1

−s

i,i+1

ˆa

i+1

−···−s

i, j

ˆa

, i = j −1,···, 1.

7.4 Estimation of an AR Model by the PARCOR Method

Assuming that the autocovariance functions C

,··· are given, Levin-

son’s algorithm of Section 7.2 can be executed by using the following