Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

VARIABLE SELECTION BY AIC 79

and reducing it to an upper triang ular matrix by a Householder transfor-

mation.

Therefore, to perform a Householder transf ormation of data length

longer than L, we ﬁrst obtain an upper triangular matrix S by putting

N = L, and then repeat the upd ate of S by adding M = L −m −1 data

elements.

On the other hand, if th e upper triangular matr ix S

has already been

obtained from a new data set {y

,···,x

}, n = N + 1,···,N + M,

then we deﬁne a 2(m + 1) ×(m + 1) matrix by





, (5.28)

and by reducing it to upper triangular fo rm, we can obtain the same ma-

trix as S

′

For M ≫ m, since the number of rows o f the matrix X

is smaller

than the number of rows of X

and X

, the amount of computation for the

Householder transformation of X

is signiﬁcantly less than that required

for th e oth e r methods. Th is metho d w ill be used in Chapter 8 to ﬁt a

locally stationary AR model.

5.5 Varia ble Select ion by AIC

In Section 5.3, the method of selection of the orde r for the model by AIC

was explained. However, in that section, it was implicitly assumed that

the order of adopting the explanatory variables was provided beforehand,

and only a model o f the form

∑

i=1

(5.29)

was considered.

This method of selecting variables is quite natural for the autoregres-

sive model shown in Section 6.1 and the polynomial regression model

shown in Section 11.1. However, with respect to a multivariate regres-

sion model and multivariate tim e series models, the orde r of adopting

variables as explanatory variables is not generally provided beforehand.

Assuming that (ℓ

,···,ℓ

) is an index vector th at indicates the order of

adopting the explanatory variables, the optimal model could be selected

among models of the form

∑

i=1

ℓ

n,ℓ

. (5.30)

80 THE LEAST SQUARES METHOD

In this case, even if the order j is provided, there are

different

models, depending o n the index vector. Such a model is called a subset

regression model. To ﬁt subset regre ssion models with explanator y vari-

ables in the order of (ℓ

,···, ℓ

), transform the uppe r triangular matrix S

to the matrix T that co nsists of m+1 column vectors with the numbers of

non-ze ro elem ents given by j

,···, j

, respectively, by the Householder

transformation. Here, j

,···, j

is the inverse function of the index vec-

tor (ℓ

,···,ℓ

), satisfying ℓ

= i.

Example For the case of m = 4 and (ℓ

,ℓ

) = (2,4,3,1), it

becomes ( j

,···, j

) = (4,1,3, 2) and the matrix T is given by

T =







0 t

0 0 0 t

0 0 0 0 t







. (5.31)

Then, the residual variance an d the AIC of the model that uses the j

explanatory variables {x

,···, x

} are given by

(ℓ

,···, ℓ

) =

m+1

∑

i= j+1

i,m+1

AIC(ℓ

,···, ℓ

) = N log2

(ℓ

,···, ℓ

) + N + 2 ( j + 1).

(5.32)

Regression coefﬁcients are then obtained by solving the linea r e quation







1,ℓ

··· t

1,ℓ

O t

j,ℓ













ℓ













1,m+1

j,m+1







(5.33)

by backward substitution.

However, in actual computation, it is not ne cessary to exchange the

order of explanatory variables and red uce the matrix to upper triangular

form. We can easily o btain them from the upper triangular matrix T of

(5.31) by the following backward sub stitution:

ˆa

ℓ

= t

−1

j,ℓ

j,m+1

(5.34)

ˆa

ℓ

= t

−1

i,ℓ

i,m+1

−t

i,ℓ

ˆa

ℓ

−···−t

i,ℓ

ˆa

ℓ

), i = j −1, ···,1.

VARIABLE SELECTION BY AIC 81

Problems

1. Obtain the AIC when the variance

is known in the regression

model in (5.1).

2. Assume that N pairs of d ata {x

},.. . ,{x

} are given.

(1) Obtain the least squares estimates ˆa and

b of the second-order

polynomial regression model y

= ax

+ bx

that passes

through the origin.

(2) Obtain a second-order polynomial regression model tha t passes

through the origin and the point (c,0), and consider how to ob-

tain the least squares estimate of the mod el.

Chapter 6

Analysis of Time Series Using

ARMA Models

The features of time series can b e concisely described using time series

models. I n this chapter, we co nsider methods for obtaining the impulse

response function, the autocovariance function, the partial autocorrela-

tion (PARCOR), the power spectrum and the roots of the characteristic

equation from the univariate ARMA model (Box and Jenk ins ( 1970),

Brockwell and Davis (1991), Shumway and Stoffer (2000)). The rela-

tions between the AR coefﬁcients and the PARCORs are also shown.

Further, methods of obtainin g the cross spectrum and the relative power

contribution based on the multivariate AR model are presented.

6.1 ARMA Model

A model that expresses a time series y

as a linear combination of past

observations y

n−i

and white noise v

n−i

is called an autoregressive mov-

ing average model (ARMA model),

∑

i=1

n−i

+ v

−

ℓ

∑

i=1

n−i

. (6.1)

Here, m an d a

are called the autoregre ssive order and the autoregres-

sive coefﬁcient (AR coefﬁcient), respectively. Similarly, ℓ and b

denote

the moving average order a nd the moving average coefﬁcient (MA co-

efﬁcient), respectively. The AR order and the MA order (m,ℓ) taken to-

gether are called the ARMA order. Further, we assume that v

is a white

noise th a t follows a n ormal distribution with mean 0 and variance

and

is independent of the past time series y

n−i

. That is, v

satisﬁes

E(v

) = 0,

E(v

) =

E(v

) = 0, for n 6= m

E(v

) = 0, for n > m.

(6.2)

84 ANALYSIS OF TIME SERIES USING ARMA MODELS

A time series y

that follows an ARMA model is called an ARMA

process. I n practical terms, the most important model is an AR model

(autoregressive model) of order m that expresses the time series as a

linear combination of the past values y

n−i

and the white noise v

and is

obtained by putting ℓ = 0,

∑

i=1

n−i

+ v

. (6.3)

On the other hand, the model obtained by putting m = 0,

= v

−

ℓ

∑

i=1

n−i

, (6.4)

is called the moving average model (MA model) of order ℓ.

It should be noted that almost all analysis of stationary time series

can be achieved by the use of AR models.

6.2 The Impulse Response Function

Using the time shift operator (or lag operator) B deﬁned by By

≡ y

n−1

the ARMA mod el can be expressed as



1 −

∑

i=1





1 −

ℓ

∑

i=1



. (6.5)

Here, let the AR operator a nd the MA operator be deﬁned, respectively,

a(B) ≡



1 −

∑

i=1



, b(B) ≡



1 −

ℓ

∑

i=1



then the ARMA model can be concisely expressed as

a(B)y

= b(B)v

. (6.6)

Dividing both sides of (6.6) by a(B), the ARMA model can be ex-

pressed as y

= a(B)

−1

b(B)v

. T herefore, if we deﬁne g(B) as a formal

inﬁnite series

g(B) ≡ a(B)

−1

b(B) =

∞

∑

i=0

, (6.7)

THE AUTOCOVARIAN CE FUNCTION 85

the time series y

that follows the ARMA mo del can be expressed by a

moving average model with inﬁnite ord er

= g(B)v

∞

∑

i=0

n−i

, (6.8)

i.e., a linear combination of present and pa st realizations of wh ite noise

The coefﬁcients g

; i = 0,1, ···, correspond to the inﬂuence of the

noise at time n = 0 to the time series at time i, and g

is called the impulse

response function of the ARMA model. Here, the impulse response g

obtained by the following recursive formula:

= 1

∑

j=1

i−j

−b

, i = 1,2,···, (6.9)

where a

= 0 for j > m and b

= 0 for j > ℓ.

Example Consider the following four models:

(a) The ﬁrst orde r AR model: y

= 0.9y

n−1

+ v

(b) The second o rder AR model: y

= 0.9

√

n−1

−0.81y

n−2

+ v

= v

−0.9

√

n−1

+ 0.81v

n−2

(d) The ARMA model with order (2,2):

= 0.9

√

n−1

−0.81y

n−2

+ v

−0.9

√

n−1

+ 0.81v

n−2

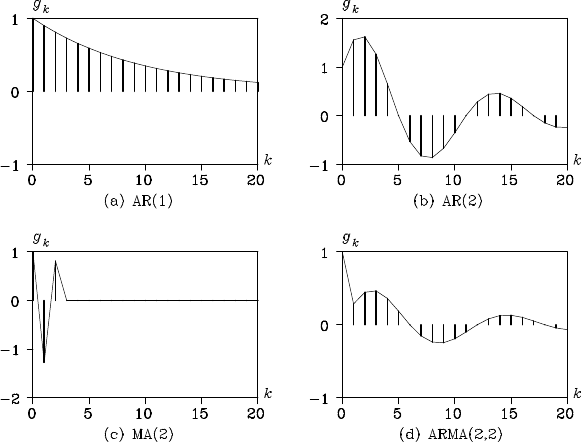
The plots (a), (b), (c ) and (d) of Figure 6.1 show the impulse response

functions obtained from (6.9) for the four models. The impulse response

function of the MA model is non-zero only for the initial ℓ p oints. On the

other han d, if the model contains AR pa rt, the impulse resp onse function

has non-zero values a lthough it gradually decays.

6.3 The Autocovariance Function

Taking the expectation after multiplying by y

n−k

on both sides of (6.1),

yields

E(y

n−k

) =

∑

i=1

E(y

n−i

n−k

)+E(v

n−k

)−

ℓ

∑

i=1

E(v

n−i

n−k

). (6.10)

Here, fr om the expression of the ARMA model using the impulse re-

sponse given in (6.7), the covariance b etween the time series y

and the

86 ANALYSIS OF TIME SERIES USING ARMA MODELS

Figure 6.1: Impulse response f unctions of four models.

white noise v

is given by

E(v

) =

∞

∑

i=0

E(v

m−i

) =

(

0 n > m

m−n

n ≤ m

. (6.11)

We obtain the following equation with r e spect to the autocovariance

function C

≡ E(y

n−k

∑

i=1



1 −

ℓ

∑

i=1



(6.12)

∑

i=1

k−i

−

ℓ

∑

i=1

i−k

, k = 1,2,···.

Therefore, if the orders m and ℓ, the autoregressive and moving

average coefﬁcients a

and b

, and the in novation variance

of the

ARMA model a re given, we ﬁrst compute the impulse response function

,···, g

ℓ

by (6.9) and then obtain the autocovariance function C

,···

THE AUTOCOVARIAN CE FUNCTION 87

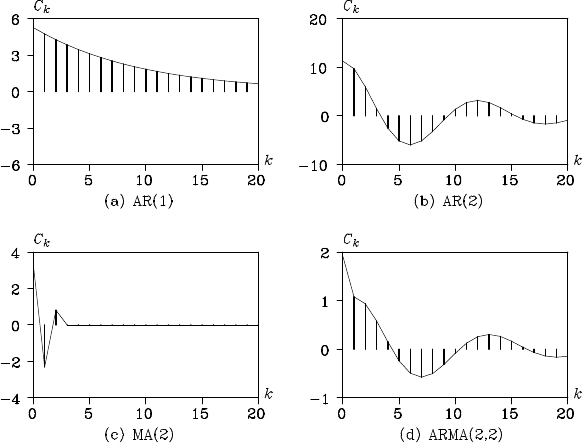
Figure 6.2: Autocovariance functions of the four models.

by solving (6.13) . In particular, the following equation f or the AR model

obtained by putting ℓ = 0 is called the Yule-Walker equation

∑

i=1

∑

i=1

k−i

. (6.13)

Note that, since for univariate time series, the autocovariance f unction

satisﬁes C

−k

= C

, the backward model satiﬁes the same equation .

Example Figure 6.2 shows the autocovariance functions of the four

models (a), (b), (c) and (d) shown in Figure 6.1. The autocovariance

functions of (b) and (d) in dicate a damped oscillation. O n the o ther hand,

for the MA model shown in (c), the autocovariance function becomes

= 0 for k > 2.

88 ANALYSIS OF TIME SERIES USING ARMA MODELS

6.4 The Relation Between AR Coefﬁcients and the PARCOR

As shown in Appe ndix B in this book, the following re la tion holds be-

tween the coe fﬁcients of the AR model with order m −1, a

m−1

, and the

coefﬁcient a

of the AR model with order m

= a

m−1

−a

m−1

m−i

, i = 1, ···,m −1. (6.14)

The coefﬁcient a

is called the m-th PARCOR (partial a utocorre-

lation coefﬁcient). If the M PARCORs, a

,···, a

, are given, repeated

application of Eq. (6.14) yields the entire set of coefﬁcients of the AR

models with orders 2 through M. On the other hand, it can b e seen from

(6.14) that, if the coefﬁcients a

,···, a

of the AR model of the highest

order are given, by solving the e quations

= a

m−1

−a



m−j

+ a

m−1



(6.15)

for j = i and m −i, the coefﬁcients of the AR model with order m −1 are

obtained by

m−1

+ a

m−i

1 −(a

)

. (6.16)

The PARCORs a

,···, a

can be obtained by repeating the above

computation. This argumen t reveals that estimation of the coefﬁcients

,···, a

of the AR model of order m is equivalent to estimation of the

PARCORs up to the order m, a

,···, a

Example Figure 6.3 shows the PARCORs of the four mo dels (a) , (b) ,

= 0 for

i > m for the AR model with order m, and they gradually decay in th e

cases of the MA model and the ARMA model.

6.5 The Power Spectr um of the ARMA Process

If an ARMA model of a time series is given, the power spectr um, as

well a s the au tocovariance function, can be obta ined. Actually, the power

spectrum of the ARMA process (6.1) can be ob ta ined from (6.8) as

p( f ) =

∞

∑

k=−∞

−2

ik f

(6.17)

∞

∑

k=−∞

E(y

n−k

−2

ik f