Gebali F. Analysis Of Computer And Communication Networks
Подождите немного. Документ загружается.

6.12 Weakly Periodic Markov Chains 207
where n > 30. As a verification, we chose
s(0) =
0.20.20.20.20.20
t
and found the following distribution vectors
s(30) =
0.2349 0.1651 0.3105 0.0895 0.1179 0.0821
t
s(31) =
0.1175 0.0825 0.3105 0.0895 0.2358 0.1642
t
s(32) =
0.2349 0.1651 0.1552 0.0448 0.2358 0.1642
t
s(33) =
0.2349 0.1651 0.3105 0.0895 0.1179 0.0821
t
s(34) =
0.1175 0.0825 0.3105 0.0895 0.2358 0.1642
t
We see that the distribution vector repeats itself with a period of three iterations.
Specifically, we see that s(30) = s(33), s(31) = s(34), and so on.
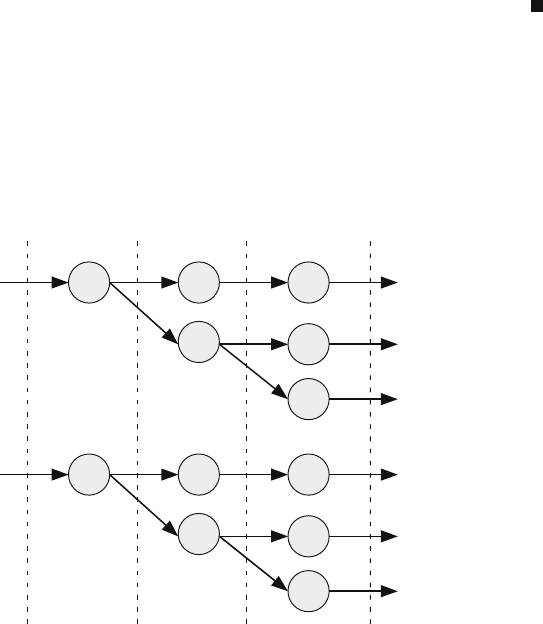
Example 6.10 Assume a wireless packet transmission system that employs an adap-
tive forward error correction scheme. There are two levels of data forward error
correction that could be employed depending on the number of errors detected
in the received packet as shown in Fig. 6.7. The upper row of states corresponds
to lower error levels and the lower row of states corresponds to higher error
levels.
Transmission
in channel
Reception/
adaptation
AFEC
coding
to s
1
s
1
s
4
s
3
s
7
s
8
s
9
s
2
s
5
s
6
s
12
s
11
s
10
to s
1
to s
2
to s
1
to s
2
to s
2
Fig. 6.7 An adaptive forward error correction scheme that uses two levels of encoding depending
on the number of errors introduced in the channel

208 6 Periodic Markov Chains
For example, if the coder is in state s
1
and errors occur during transmission, we
move to state s
4
. If the receiver is able to correct the errors, we move to state s
8
.
We then conclude that the error correction coding is adequate, and we move to state
s
1
for the next transmission. If the errors cannot be corrected, we conclude that the
error coding is not adequate and we move from state s
9
to s
2
at the next transmission.
Write down the transition matrix and show that it corresponds to a weakly peri-
odic Markov chain.
The sets of periodic states are identified at the bottom of the figure. We can see
that we have three sets of states such that the states in each set make transitions
only to the next set. This seems to imply a weakly periodic Markov chain. As a
verification, we construct the transition matrix and see its structure.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0000p
15
p
16
0000p
25
p
26
p
31
p
32
0000
p
41
p
42
0000
00p
53
p
54
00
00p
63
p
64
00
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
We see that the transition matrix has the same structure as a weakly periodic
Markov chain with period γ = 3. The exact values of the transition probabilities
will depend on the details of the system being investigated.
6.13 Reducible Periodic Markov Chains
A reducible periodic Markov chain is one in which the transition matrix can be
partitioned into the canonic form
P =
⎡
⎣
CA
0T
⎤
⎦
(6.59)
where
C = square column stochastic periodic matrix
A = rectangular nonnegative matrix
T = square column substochastic matrix
Some of the eigenvalues of the transition matrix will lie on the unit circle. The
other eigenvalues will be inside the unit circle as shown in Fig. 6.8. Note that the
periodic matrix C could be strongly periodic or could be weakly periodic.

6.13 Reducible Periodic Markov Chains 209
Fig. 6.8 The eigenvalues of a
reducible periodic Markov
chain. Some of the
eigenvalues lie on the unit
circle in the complex plane
and some lie inside the unit
circle
Complex plane
Unit circle
Re
Im
Example 6.11 Check to see if the given matrix below corresponds to a reducible
periodic Markov chain.
P =
1
2
3
4
5
12 34 5
⎡
⎢
⎢
⎢
⎢
⎣
00.100.11
00.300.20
10.200.20
00.300.40
00.110.10
⎤
⎥
⎥
⎥
⎥
⎦
where the state indices are indicated around P for illustration. Rearrange the rows
and columns to express the matrix in the form of (6.59) and identify the matrices C,
A, and T. Verify the assertions that C is column stochastic, A is nonnegative, and T
is column substochastic.
The best way to study a Markov chain is to explore its eigenvalues.
λ
1
= exp
j2π ×
1
3
λ
2
= exp
j2π ×
2
3
λ
3
= exp
j2π ×
3
3
λ
4
= 0.6exp
(
j2π
)
λ
5
= 0.1exp
(
j2π
)
Thus we see that we have two decaying modes, but three other eigenvalues lie on
the unit circle. We classify this system as a weakly periodic Markov chain.
The vector corresponding to the unity eigenvalue is given by
x =
0.5774 0 0.5774 0 0.5774
t
210 6 Periodic Markov Chains
The zero components of the eigenvector indicate that we have transient states,
namely s
2
and s
4
. The fact that we have only one eigenvalue, that is unity, indicates
that we have one set only of closed states: C = 1, 3, and 5. Based on that, we
further classify this system as reducible weakly periodic Markov chain.
We cluster states 1, 3, and 5 together since they correspond to the closed states,
and cluster states 2 and 4 together since they correspond to the transient states.
We perform this rearranging through the elementary exchange matrix E(2, 5) which
exchanges states 2 and 5:
E(2, 5) =
⎡
⎢
⎢
⎢
⎢
⎣
10000
00001
00100
00010
01000
⎤
⎥
⎥
⎥
⎥
⎦
The exchange of states is achieved by pre- and post-multiplying the transition
matrix:
P
= E(2, 5) PE(2, 5)
This results in
P
=
1
5
3
4
2
15 34 2
⎡
⎢
⎢
⎢
⎢
⎣
0100.10.1
0010.10.1
1000.20.2
0000.40.1
0000.20.3
⎤
⎥
⎥
⎥
⎥
⎦
We see that the transition matrix represents a reducible periodic Markov chain,
and matrices C, A, and T are
C =
⎡
⎣
010
001
100
⎤
⎦
A =
⎡
⎣
0.10.1
0.10.1
0.20.2
⎤
⎦
T =
0.50.1
0.20.3
The sum of each column of C is exactly 1, which indicates that it is column
stochastic and strongly periodic. The sum of columns of T is less than 1, which
indicates that it is column substochastic.

6.14 Transient Analysis 211
The set of closed periodic states is C ={
1, 3, 5
}, and the set of transient states
is T ={
2, 4
}
Starting in state 2 or 4, we will ultimately go to states 1, 3, or 5. Once we are
there, we cannot ever go back to state 2 or 4 because we entered the closed periodic
states.
6.14 Transient Analysis
After n time steps, the transition matrix of a reducible Markov chain will still be
reducible and will have the form
P
n
=
C
n
Y
n
0T
n
(6.60)
where matrix Y
n
is given by
Y
n
=
n−1
i=0
C
n−i−1
AT
i
(6.61)
We can always find C
n
and T
n
using the techniques discussed in Chapter 3 such
as diagonalization, finding the Jordan canonic form, or even repeated multiplica-
tions.
The stochastic matrix C
n
can be expressed in terms of its eigenvalues using (3.80)
on page 94.
C
n
= C
1
+λ
n
2
C
2
+λ
n
3
C
3
+··· (6.62)
where it was assumed that C
1
is the expansion matrix corresponding to the eigen-
value λ
1
= 1.
Similarly, the substochastic matrix T
n
can be expressed in terms of its eigenval-
ues using (3.80) on page 94.
T
n
= λ
n
1
T
1
+λ
n
2
T
2
+λ
n
3
T
3
+··· (6.63)
Equation (6.61) can then be expressed in the form
Y
n
=
m
j=1
C
j
A
n−1
i=0
λ
n−i−1
j
T
i
(6.64)
After some algebraic manipulations, we arrive at the form
Y
n
=
m
j=1
λ
n−1
j
C
j
A
I −
T
λ
j
n
I −
T
λ
j
−1
(6.65)

212 6 Periodic Markov Chains
This can be written in the form
Y
n
= C
1
A
(
I −T
)
−1
I −T
n
+
λ
n−1
2
C
2
A
I −
1
λ
2
T
−1
I −
1
λ
n
2
T
n
+
λ
n−1
3
C
3
A
I −
1
λ
3
T
−1
I −
1
λ
n
3
T
n
+··· (6.66)
If some of the eigenvalues of C are repeated, then the above formula has to be
modified as explained in Section 3.14 on page 103.
Example 6.12 Consider the reducible weakly periodic Markov chain of the pre-
vious example. Assume that the system was initially in state 4. Explore how the
distribution vector changes as time progresses.
We do not have to rearrange the transition matrix to do this example. We have
P =
⎡
⎢
⎢
⎢
⎢
⎣
00.100.11
00.300.20
10.200.20
00.300.40
00.110.10
⎤
⎥
⎥
⎥
⎥
⎦
The eigenvalues for this matrix are
λ
1
= exp
j2π ×
1
3
λ
2
= exp
j2π ×
2
3
λ
3
= exp
j2π ×
3
3
λ
4
= 0.1exp
j2π ×
3
3
We see that the period of this system is γ = 3. The initial distribution vector is
s =
0010
t
The distribution vector at the start is given by
s(0) =
00010
t
s(1) =
0.1000 0.2000 0.2000 0.4000 0.1000
t
s(2) =
0.1600 0.1400 0.2200 0.2200 0.2600
t

6.15 Asymptotic Behavior 213
s(3) =
0.2960 0.0860 0.2320 0.1300 0.2560
t
s(4) =
0.2776 0.0518 0.3392 0.0778 0.2536
t
s(5) =
0.2666 0.0311 0.3035 0.0467 0.3522
t
Continuing the iterations, the distribution vector settles down to the following
sequence.
s(19) =
0.3265 0.0000 0.3775 0.0000 0.2959
t
s(20) =
0.2959 0.0000 0.3265 0.0000 0.3775
t
s(21) =
0.3775 0.0000 0.2959 0.0000 0.3265
t
s(22) =
0.3265 0.0000 0.3775 0.0000 0.2959
t
s(23) =
0.2959 0.0000 0.3265 0.0000 0.3775
t
s(24) =
0.3775 0.0000 0.2959 0.0000 0.3265
t
We note that after about 20 time steps, the probability of being in the tran-
sient state 2 or 4 is nil. The system will definitely be in the closed set composed
of states 1, 3, or 5. The distribution vector will show periodic behavior with a
period γ = 3.
6.15 Asymptotic Behavior
Assume we have a reducible periodic Markov chain with transition matrix P that is
expressed in the form
P =
CA
0T
(6.67)
According to (6.60), after n time steps, the transition matrix will have the form
P
n
=
C
n
Y
n
0T
n
(6.68)
where matrix Y
n
is given by (6.65) in the form
Y
n
=
m
j=1
λ
n−1
j
C
j
A
I −
T
λ
j
n
I −
T
λ
j
−1
(6.69)
214 6 Periodic Markov Chains
when n →∞; T
n
will become zero since it is column substochastic. Further-
more, the eigenvalues of C satisfy the following equations because of the periodicity
of C.
|
λ
i
|
= 11≤ i ≤ K (6.70)
|
λ
i
|
< 1 K < i ≤ m (6.71)
The eigenvalues that lie in the unit circle will have no contribution at large values
of n, and matrix P
∞
becomes
P
∞
=
EF
00
(6.72)
The matrices E and F are given by
E =
K
k=1
λ
i
k
C
k
(6.73)
F =
γ
i=1
K
k=1
λ
i−1
k
C
k
AT
i−1
(
I −T
γ
)
−1
(6.74)
where I is the unit matrix whose dimensions match that of T.
Example 6.13 Find the asymptotic transition matrix for the reducible weakly peri-
odic Markov chain characterized by the transition matrix
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
000.90.10.10.30.1
000.10.90.20.10.3
0.20.80000.10
0.80.2000.10 0.1
00000.20.20.1
00000.10.10
00000.30.20.4
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
The components of the transition matrix are
C =
⎡
⎢
⎢
⎣
000.90.1
000.10.9
0.20.
80 0
0.80.20 0
⎤
⎥
⎥
⎦
6.15 Asymptotic Behavior 215
A =
⎡
⎢
⎢
⎣
0.10.30.1
0.20.10.3
00.10
0.10 0.1
⎤
⎥
⎥
⎦
T =
⎡
⎣
0.20.20.1
0.10.10
0.30.20.4
⎤
⎦
C is a weakly periodic Markov chain whose eigenvalues are
λ
1
= 1
λ
2
=−1
λ
3
= 0.6928 j
λ
3
=−0.6928 j
and C
i
can be decomposed into the form
C
i
= C
1
+(−1)
i
C
2
where
C
1
=
⎡
⎢
⎢
⎣
0.25 0.25 0.25 0.25
0.25 0.25 0.25 0.25
0.25 0.25 0.25 0.25
0.25 0.25 0.25 0.25
⎤
⎥
⎥
⎦
C
2
=
⎡
⎢
⎢
⎣
0.25 0.25 −0.25 −0.25
0.25 0.25 −0.25 −0.25
−0.25 −0.25 0.25 0.25
−0.25 −0.25 0.25 0.25
⎤
⎥
⎥
⎦
According to (6.72), the matrix E has the value
E =
⎡
⎢
⎢
⎣
0.2742 0.3044 0.3018
0.2742 0.3044 0.3018
0.2258 0.1956 0.1982
0.2258 0.1956 0.1982
⎤
⎥
⎥
⎦
According to (6.72), the matrix
F has the value
F =
⎡
⎢
⎢
⎣
0.2742 0.3044 0.3018
0.2742 0.3044 0.3018
0.2258 0.1956 0.1982
0.2258 0.1956 0.1982
⎤
⎥
⎥
⎦

216 6 Periodic Markov Chains
The asymptotic value of P is given by the two values
P
1
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.50.50 0 0.2258 0.1956 0.1982
0.50.50 0 0.2258 0.1956 0.1982
000.50.50.2742 0.3044 0.3018
000.50.50.2742 0.3044 0.3018
00000 0 0
00000 0 0
00000 0 0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
P
2
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
000.50.50.2742 0.3044 0.3018
000.50.50.2742 0.3044 0.3018
0.50.50 0 0.2258 0.1956 0.1982
0.50.50 0 0.2258 0.1956 0.1982
00000 0 0
00000 0 0
00000 0 0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
At steady state, the two matrices are related by
P
1
= PP
2
P
1
= PP
1
Therefore, at steady state, the system oscillates between two state transition ma-
trices and periodic behavior is observed.
We can make several observations on the asymptotic value of the transition
matrix.
(a) The columns are not identical as in nonperiodic Markov chains.
(b) There is no possibility of moving to a transient state irrespective of the value of
the initial distribution vector.
(c) The asymptotic values of the transition matrix has two forms P
1
and P
2
such
that the system makes periodic transitions between the states, and a steady-state
value can never be reached.
6.16 Identification of Markov Chains
e are now able to discuss how we can determine if the given transition matrix cor-
responds to a periodic Markov chain or not and to determine if the chain is strongly
or weakly periodic. Further, we are also able to tell if the Markov chain is reducible
or irreducible and to identify the transient and closed states.
