Gebali F. Analysis Of Computer And Communication Networks
Подождите немного. Документ загружается.

6.10 Transition Diagram 197
This matrix can be obtained by proper ordering of the states and will have a period
γ = m, which can be easily proved (see Problem 5).This matrix is also known as
a circulant matrix since multiplying any matrix by this matrix will shift the rows or
columns by one location.
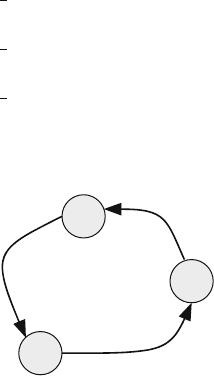
6.10 Transition Diagram
Based on the above theorems, specifying the structure of a strongly periodic Markov
chain, we find that the transition diagram for a strongly periodic Markov chain of
period γ = 3 is as shown in Fig. 6.5. We see that each set of periodic classes
consists of one state only, and the number of states equals the period of the Markov
chain.
Example 6.5 Prove that the given transition matrix is periodic and determine the
period.
P =
⎡
⎢
⎢
⎢
⎢
⎣
01000
00001
10000
00100
00010
⎤
⎥
⎥
⎥
⎥
⎦
The given matrix is column stochastic, full rank, and all its rows and columns
are zeros except for five elements that contain 1 at unique locations in each row
and column. Thus P is periodic according to Theorem 6.6. From MATLAB, the
eigenvalues of P are given by
λ
1
= 1∠144
◦
= exp
j2π ×
2
5
λ
2
= 1∠ − 144
◦
= exp
j2π ×
3
5
λ
3
= 1∠72
◦
= exp
j2π ×
1
5
Fig. 6.5 Transition diagram
for a strongly periodic
Markov chain with period
γ = 3
S
2
S
1
S
3

198 6 Periodic Markov Chains
λ
4
= 1∠ − 72
◦
= exp
j2π ×
4
5
λ
5
= 1∠0
◦
= exp
j2π ×
5
5
Thus the period is γ = 5. As a verification, MATLAB assures us that P
5
= I.
6.11 Composite Strongly Periodic Markov Chains
In general, a composite strongly periodic Markov chain can be expressed, through
proper ordering of states, in the canonic form
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
C
1
00··· 00
0C
2
0 ··· 00
00C
3
··· 00
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· C
h−1
0
000··· 0C
h
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(6.48)
where C
i
is an m
i
× m
i
circulant matrix whose period is γ
i
= m
i
. The period of
the composite Markov chain is given by the equation
γ = lcm
(
γ
1
,γ
2
, ···,γ
h
)
(6.49)
Figure 6.6 shows the periodic classes of a composite strongly periodic Markov
chain. The states are divided into noncommunicating sets of periodic
classes.
Fig. 6.6 Transition diagram
for a composite strongly
periodic Markov chain. The
states are divided into
noncommunicating sets of
periodic classes
S
2
S
4
S
5
S
1
S
3
S
7
S
8
S
9
S
6
6.11 Composite Strongly Periodic Markov Chains 199
Example 6.6 Find the period of the following periodic transition matrix
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0001000
1000000
0100000
0010000
0000001
0000100
0000010
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
We identify C
1
as a circulant 4 × 4 matrix with period γ
1
= 4, and we identify
C
2
as a circulant 3 × 3 matrix with period γ
2
= 3. Indeed, the eigenvalues of
P are
λ
1
= 1∠180
◦
= exp
j2π ×
2
4
λ
2
= 1∠90
◦
= exp
j2π ×
1
4
λ
3
= 1∠ − 90
◦
= exp
j2π ×
3
4
λ
4
= 1∠0
◦
= exp
j2π ×
4
4
λ
5
= 1∠120
◦
= exp
j2π ×
1
3
λ
6
= 1∠ − 120
◦
= exp
j2π ×
2
3
λ
7
= 1∠0
◦
= exp
j2π ×
3
3
We expect P to have a period equal to the least common multiple of 3 and 4,
which is 12. Indeed, this is verified by MATLAB where the smallest power k for
which P
k
= I is when k = 12.
Example 6.7 Find the period of the following transition matrix for a strongly peri-
odic Markov chain and express P in the form given by (6.48).

200 6 Periodic Markov Chains
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
000100000
000000010
100000000
001000000
000000100
000000001
000001000
010000000
000010000
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
By inspection, we know that the given matrix is periodic since the elements are
either 1 or 0 and each row or column has a single 1 at a unique location.
Indeed, all the eigenvalues of P lie on the unit circle
λ
1
= 1∠120
◦
= exp
j2π ×
1
3
λ
2
= 1∠ − 120
◦
= exp
j2π ×
2
3
λ
3
= 1∠0
◦
= exp
j2π ×
3
3
λ
4
= 1∠0
◦
= exp
j2π ×
2
2
λ
5
= 1∠180
◦
= exp
j2π ×
1
2
λ
6
= 1∠180
◦
= exp
j2π ×
2
4
λ
7
= 1∠90
◦
= exp
j2π ×
1
4
λ
8
= 1∠ − 90
◦
= exp
j2π ×
3
4
λ
9
= 1∠0
◦
= exp
j2π ×
4
4
Using MATLAB, we find that P
3
= I, P
2
= I, and P
4
= I. However, the LCM
of 2, 3, and 4 is 12 and P
12
= I.
We notice that there are three eigenvalues equal to 1; mainly
λ
3
= λ
4
= λ
9
= 1
6.11 Composite Strongly Periodic Markov Chains 201
The eigenvectors corresponding to these eigenvalues give three sets of periodic
classes:
C
1
={1, 3, 4}
C
2
={2, 8}
C
3
={5, 6, 7, 9}
Each set is identified by the nonzero components of the corresponding eigen-
vector.
To group each set of periodic states together, we exchange states 2 and 4 so
that C
1
will contain the new states 1, 3, and 4. This is done using the elementary
exchange matrix
E(2, 4) =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
100000000
000100000
001000000
010000000
000010000
000001000
000000100
000000010
000000001
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
The new matrix will be obtained with the operations
P
= E(2, 4) ×P ×E(2, 4)
Next, we group the states of C
2
together by exchanging states 5 and 8 so that C
2
will contain the new states 2 and 8, and C
3
will contain the states 5, 6, 7, and 9. The
rearranged matrix will be
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
010000000
001000000
100000000
000010000
000100000
000000001
000001000
000000100
000000010
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦

202 6 Periodic Markov Chains
From the structure of the matrix, we see that the periods of the three diagonal
circulant matrices is γ
1
= 4, γ
2
= 2, and γ
3
= 3. The period of the matrix is
γ = lcm(4, 2, 3) = 12. As a verification, we find that the first time P
n
becomes the
identity matrix when n = 12.
6.12 Weakly Periodic Markov Chains
Periodic behavior can sometimes be observed in Markov chains even when some
of the eigenvalues of P lie on the unit circle while other eigenvalues lie inside the
unit circle. In spite of that, periodic behavior is observed because the structure of the
matrix is closely related to the canonic form for a periodic Markov chain in (6.47) on
page 196. To generalize the structure of a circulant matrix, we replace each “1” with
a block matrix and obtain the canonic form for a weakly periodic Markov chain:
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
000··· 00W
h
W
1
00··· 000
0W
2
0 ··· 000
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· 000
000··· W
h−2
00
000··· 0W
h−1
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(6.50)
where the block-diagonal matrices are square zero matrices and the nonzero matri-
ces W
i
could be rectangular but the sum of each of their columns is unity since P is
column stochastic. Such a matrix will exhibit periodic behavior with a period γ = h
where h is the number of W blocks.
As an example, consider the following transition matrix
P =
⎡
⎢
⎢
⎢
⎢
⎣
000.10.60.5
000.90.40.5
0.50.2000
0.10.4000
0.40.4000
⎤
⎥
⎥
⎥
⎥
⎦
≡
0W
2
W
1
0
(6.51)
We know this matrix does not correspond to a strongly periodic Markov chain
because it is not a 0–1 matrix whose elements are 0 or 1. However, let us look at the
eigenvalues of this matrix:
λ
1
=−1
λ
2
= 1
6.12 Weakly Periodic Markov Chains 203
λ
3
= 0.3873 j
λ
4
=−0.3873 j
λ
5
= 0
Some of the eigenvalues are inside the unit circle and represent decaying modes,
but two eigenvalues lie on the unit circle. It is this extra eigenvalue on the unit circle
that is responsible for the periodic behavior.
Let us now see the long-term behavior of the matrix. When n > 25, the contri-
bution of the decaying modes will be < 10
−10
. So let us see how P
n
behaves when
n > 25.
P
25
=
⎡
⎢
⎢
⎢
⎢
⎣
000.40.40.4
000.60.60.6
0.32 0.32000
0.28 0.28000
0.40 0.40000
⎤
⎥
⎥
⎥
⎥
⎦
(6.52)
P
26
=
⎡
⎢
⎢
⎢
⎢
⎣
0.28 0.28000
0.40 0.40000
000.40.40.4
000.60.60.6
0.32 0.32000
⎤
⎥
⎥
⎥
⎥
⎦
(6.53)
P
27
=
⎡
⎢
⎢
⎢
⎢
⎣
000.40.40.4
000.60.60.6
0.32 0.32000
0.28 0.28000
0.40 0.40000
⎤
⎥
⎥
⎥
⎥
⎦
(6.54)
We see that P
n
repeats its structure every two iterations.
We can make several observations about this transition matrix:
1. The transition matrix displays periodic behavior for large value of n.
2. P
n
has a block structure that does not disappear. The blocks just move vertically
at different places after each iteration.
3. The columns of each block in P
n
are identical and the distribution vector will be
independent of its initial value.
4. The period of P
n
is 2.
Let us see now the distribution vector values for n = 25, 26, and 27. The initial
value of the distribution vector is not important, and we arbitrarily pick
s(0) =
0.20.20.20.20.2
t
(6.55)
204 6 Periodic Markov Chains
We get
s(25) = P
25
s(0) =
0.240 0.360 0.128 0.112 0.160
t
(6.56)
s(26) =
0.160 0.240 0.192 0.168 0.240
t
(6.57)
s(27) =
0.240 0.360 0.128 0.112 0.160
t
(6.58)
We notice that the distribution vector repeats its value for every two iterations.
Specifically, we see that s(25) = s(27), and so on.
Example 6.8 The following transition matrix can be expressed in the form of (6.50).
Find this form and estimate the period of the Markov chain.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
00.50.1000
00.30.5000
00.20.4000
0.90 0000
0.10 0000
000111
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
Our strategy for rearranging the states is to make the diagonal zero matrices
appear in ascending order. The following ordering of states gives the desired result:
1 ↔ 62↔ 53↔ 4
The rearranged matrix will be
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
000111
0.10 0000
0.90 0000
00.20.4000
00.30.5000
00.50.1000
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
The structure of the matrix is now seen to be in the form
P =
⎡
⎣
00W
3
W
1
00
0W
2
0
⎤
⎦
6.12 Weakly Periodic Markov Chains 205
where
W
1
=
0.1
0.9
W
2
=
⎡
⎣
0.20.4
0.30.5
0.50.1
⎤
⎦
W
3
=
111
The eigenvalues for P are
λ
1
= exp
j2π ×
1
3
λ
2
= exp
j2π ×
2
3
λ
3
= 1 = exp
j2π ×
3
3
λ
4
= 0
λ
5
= 0
λ
6
= 0
The period of P is 3. As a verification, we chose
s(0) =
0.20.20.20.20.20
t
and found the following distribution vectors
s(3) =
0.2000 0.0400 0.3600 0.1520 0.1920 0.0560
t
s(4) =
0.4000 0.0200 0.1800 0.1520 0.1920 0.0560
t
s(5) =
0.4000 0.0400 0.3600 0.0760 0.0960 0.0280
t
s(6) =
0.2000 0.0400 0.3600 0.1520 0.1920 0.0560
t
s(7) =
0.4000 0.0200 0.1800 0.1520 0.1920 0.0560
t
We see that the distribution vector repeats itself over a period of three iterations.
Specifically, we see that s(3) = s(6), s(4) = s(7), and so on.

206 6 Periodic Markov Chains
Example 6.9 The following transition matrix has the form of (6.50). Estimate the
period of the Markov chain and study the distribution vector after the transients have
decayed.
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
00000.31
00000.70
0.90.60000
0.10.40000
000.50.900
000.50.100
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
The eigenvalues for this matrix are
λ
1
= exp
j2π ×
1
3
λ
2
= exp
j2π ×
2
3
λ
3
= 1 = exp
j2π ×
3
3
λ
4
= 0.438 exp
j2π ×
1
3
λ
5
= 0.438 exp
j2π ×
2
3
λ
6
= 0.438 exp
j2π ×
3
3
The period of this matrix is γ = 3.
The transients would die away after about 30 iterations since the value of the
eigenvalues within the unit circle would be
λ
30
= 0.438
30
= 1.879 ×10
−11
The value of P
n
at high values for n would start to approach an equilibrium
pattern
P
n
=
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.5873 0.5873 0001
0.4127 0.4127 0000
000.7762 0.7762 0 0
000.2238 0.2238 0 0
00000.5895 0.5895
00000.4105 0.4105
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
