Gebali F. Analysis Of Computer And Communication Networks
Подождите немного. Документ загружается.


6.5 The Transition Matrix Determinant 187
We start by performing repeated multiplications to see when P
k
= I for some value
of k. We are lucky since
P
2
= I
The period of this Markov chain is γ = 2. The given transition matrix is also known
as a circulant matrix where the adjacent rows or columns advance by one position.
The matrix P could also be considered a permutation matrix or exchange matrix
where rows 1 and 2 are exchanged after premultiplying any 2 ×m matrix [2].
6.5 The Transition Matrix Determinant
This section provides one specification on the transition matrix of a strongly peri-
odic Markov chain. Theorem 6.1 indicates the allowed values of the determinant of
the transition matrix.
Theorem 6.1 Let P be the transition matrix of a strongly periodic Markov chain.
The determinant of P will be given by [3]
⌬ =±1
Proof We start by assuming that the Markov chain is strongly periodic. We have
from the assumptions
P
γ
= I (6.9)
Equate the determinants of both sides
⌬
γ
= 1 (6.10)
where ⌬ is the determinant of P and ⌬
γ
is the determinant of P
γ
.
Taking the γ -root of the above equation, we find that ⌬ is the γ -root of unity:
⌬ = exp
j2π ×
k
γ
k = 1, 2, ···,γ (6.11)
But ⌬ must be real since the components of P are all real. Thus, the only possible
values for ⌬ are ±1. This proves the theorem.
From the properties of the determinant of the transition matrix of a strongly
periodic Markov chain, we conclude that P must have the following equivalent
properties:

188 6 Periodic Markov Chains
1. The m ×m transition matrix P of a strongly periodic Markov chain is full rank,
i.e., rank(P) = m.
2. The rows and columns of the transition matrix P of a strongly periodic Markov
chain are linearly independent.
3. λ<1 can never be an eigenvalue for the transition matrix P of a strongly periodic
Markov chain. Any value of λ<1 would produce a determinant that is not equal
to ±1.
4. All eigenvalues must obey the relation |λ|=1. This will be proved in the next
section.
6.6 Transition Matrix Diagonalization
The following theorem indicates that the transition matrix of a strongly periodic
Markov chain can be diagonalized. This fact naturally leads to a great simplification
in the study of strongly periodic Markov chains.
Theorem 6.2 Let P be the transition matrix of a strongly periodic Markov chain
with period γ>1. Then P is diagonalizable.
Proof If P is diagonalizable, then its Jordan canonic form will turn into a diagonal
matrix. Let us assume that P is not diagonalizable. In that case, P is similar to its
Jordan canonic form
P = UJU
−1
(6.12)
Since P is periodic, we must have
P
γ
= UJ
γ
U
−1
= I (6.13)
Multiplying both sides of the equation from the right by U, we get
UJ
γ
= IU = UI (6.14)
This implies that we must have
J
γ
= I (6.15)
The above equation states that the matrix J
γ
is equal to the diagonal matrix I.
However, J can never be diagonal if it is not already so. Thus the above equation is
only possible when the Jordan canonic form J is diagonal, which happens when P
is diagonalizable, and the theorem is proved.

6.6 Transition Matrix Diagonalization 189
Example 6.2 Verify that the following transition matrix is diagonalizable.
P =
⎡
⎢
⎢
⎣
0010
1000
0100
0001
⎤
⎥
⎥
⎦
We start by finding the Jordan canonic form for the matrix P.
[V,J] = jordan(P)
V=
0.3333 0.3333 0.3333 0
0.3333 -0.1667 - 0.2887j -0.1667 + 0.2887j 0
0.3333 -0.1667 + 0.2887j -0.1667 - 0.2887j 0
1.0000 0 0 1.0000
J=
1.0000 0 0 0
0 -0.5000 + 0.8660j 0 0
0 0 -0.5000 - 0.8660j 0
0 0 0 1.0000
Thus we see that P is diagonalizable. We also see that all the eigenvalues lie on
the unit circle.
λ
1
= exp
j2π ×
1
3
λ
2
= exp
j2π ×
2
3
λ
3
= exp
j2π ×
3
3
λ
4
= exp
j2π ×
3
3
where j =
√
−1.
The following theorem will add one more specification on the transition matrix
of a strongly periodic Markov chain.
Theorem 6.3 Let P be the transition matrix of a strongly periodic Markov chain.
Then P is unitary (orthogonal)
Proof Assume x is an eigenvector of the transition matrix P, then we can write
Px= λ x (6.16)
190 6 Periodic Markov Chains
Transposing and taking the complex conjugate of both sides of the above equa-
tion, we get
x
H
P
H
= λ
∗
x
H
(6.17)
where the symbol H indicates complex conjugate of the transposed matrix or vector,
and λ
∗
is the complex conjugate of λ.
Now multiply the corresponding sides of Equations (6.16) and (6.17) to get
x
H
P
H
Px= λ
∗
λ x
H
x (6.18)
or
x
H
P
H
Px=
|
λ
|
2
|
x
|
2
(6.19)
where
|
x
|
2
= x
∗
1
x
1
+ x
∗
2
x
2
+···+x
∗
m
x
m
(6.20)
We know from Theorem 6.5 that the eigenvalues of P lie on the unit circle, and
(6.19) can be written as
x
H
Yx=
|
x
|
2
(6.21)
where Y = P
H
P. The above equation can be written as
m
i=1
m
j=1
x
∗
i
y
ij
x
j
=
m
i=1
x
∗
i
x
i
(6.22)
This equation can only be satisfied for arbitrary values of the eigenvectors when
m
j=1
x
∗
i
y
ij
x
j
= x
∗
i
x
i
(6.23)
Similarly, this equation can only be satisfied for arbitrary values of the eigenvec-
tors when
y
ij
= δ
ij
(6.24)
where δ
ij
is the Kronecker delta which satisfies the equation
δ
ij
=
1 when i = j
0 when i = j
(6.25)

6.7 Transition Matrix Eigenvalues 191
We conclude therefore that
P
H
P = I (6.26)
Thus P is a unitary matrix whose inverse equals the complex conjugate of its
transpose. Since P is real, the unitary matrix is usually called orthogonal matrix.
This proves the theorem.
6.7 Transition Matrix Eigenvalues
So far, we have discovered several restrictions on the transition matrix of a strongly
periodic Markov chain. The following theorem specifies the allowed magnitudes of
the eigenvalues for strongly periodic Markov chains.
Theorem 6.4 Let P be the transition matrix of a Markov chain. The Markov chain
will be strongly periodic if and only if all the eigenvalues of P lie on the unit circle.
Proof Let us start by assuming that the Markov chain is strongly periodic. Accord-
ing to Theorem 6.1, the determinant of the transition matrix is
⌬ =±1
The determinant can be written as the product of all the eigenvalues of the tran-
sition matrix
⌬ =
i
λ
i
(6.27)
but we know that ⌬ =±1 and we can write
i
λ
i
=±1 (6.28)
Since P is column stochastic, all its eigenvalues must satisfy the inequality
|
λ
i
|
≤ 1 (6.29)
The above inequality together with (6.28) imply that
|
λ
i
|
= 1 (6.30)
This proves one side of the theorem.
192 6 Periodic Markov Chains
Let us now assume that all the eigenvalues of P lie on the unit circle. In that case,
we can write the eigenvalues as
λ
i
= exp
j2π
γ
i
(6.31)
Therefore, we can write the transition matrix determinant as
⌬ =
i
λ
i
(6.32)
Raising the above equation to some power γ , we get
⌬
γ
=
i
λ
γ
i
(6.33)
Thus we have
⌬
γ
= exp
j2π
γ
γ
1
+
γ
γ
2
+···+
γ
γ
m
(6.34)
If γ is chosen to satisfy the equation
γ = lcm(γ
i
) (6.35)
where lcm is the least common multiple, then we can write
⌬
γ
= 1 (6.36)
According to Theorem 6.1, this proves that the Markov chain is strongly periodic.
This proves the other part of the theorem.
Figure 6.4 shows the locations of the eigenvalues of P in the complex plane. We
see that all the eigenvalues of a strongly periodic Markov chain lie on the unit circle
as indicated by the ×s. Since P is column stochastic, the eigenvalue λ = 1must
be present as is also indicated. The figure also indicates that complex eigenvalues
appear in complex conjugate pairs.
Example 6.3 Consider the following transition matrix
P =
⎡
⎢
⎢
⎣
0010
1000
0100
0001
⎤
⎥
⎥
⎦
Verify that this matrix is strongly periodic and find its period.
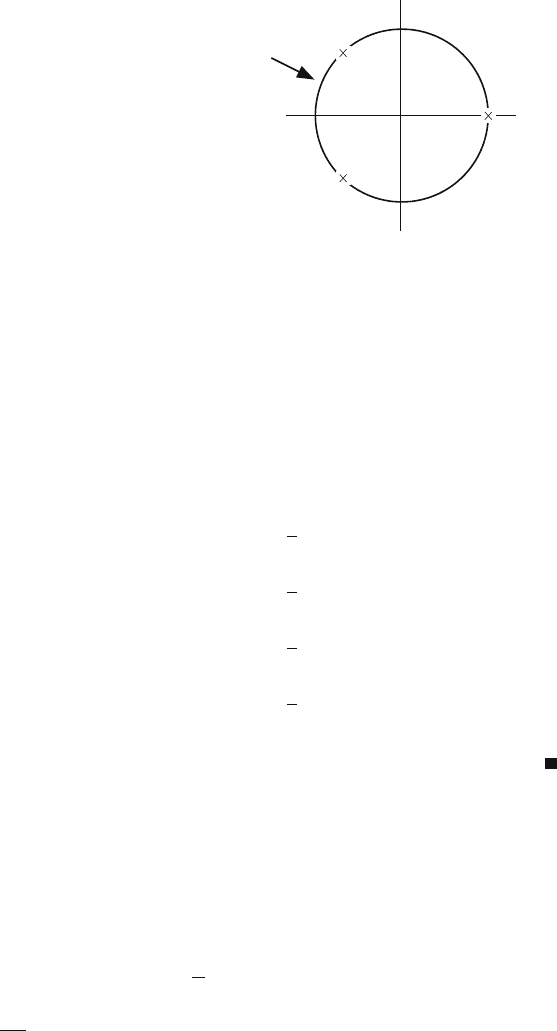
6.7 Transition Matrix Eigenvalues 193
Fig. 6.4 All the eigenvalues
of a strongly periodic Markov
chain lie on the unit circle in
the complex plane
Complex plane
Unit circle
Re
Im
The determinant is det(P) = 1, and the rank of the transition matrix is rank
(P) = 4.
Performing repeated multiplications, we find that
P
3
= I
The period of the given transition matrix is γ = 3.
The eigenvalues of the transition matrix are
λ
1
= exp
j2π ×
1
3
λ
2
= exp
j2π ×
2
3
λ
3
= exp
j2π ×
3
3
λ
4
= exp
j2π ×
3
3
Thus all the eigenvalues lie on the unit circle.
The following theorem defines the allowed eigenvalues for the transition matrix
of a strongly periodic Markov chain.
Theorem 6.5 Let P be the transition matrix of an irreducible strongly periodic
Markov chain with period γ>1. Then the eigenvalues of P are the γ -roots of
unity, i.e.,
λ
i
= exp
j2π ×
i
γ
i = 1, 2, ···,γ (6.37)
where j =
√
−1.

194 6 Periodic Markov Chains
Proof Since we proved in Theorem 6.2 that P is diagonalizable, it is similar to a
diagonal matrix D such that
P = XDX
−1
(6.38)
where X is the matrix whose columns are the eigenvectors of P, and D is the diagonal
matrix whose diagonal elements are the eigenvalues of P.
Since P is periodic, we must have
P
γ
= XD
γ
X
−1
= I (6.39)
Multiplying both sides from the right by X, we get
XD
γ
= IX = XI (6.40)
Therefore, we must have
D
γ
= I (6.41)
This implies that any diagonal element d
γ
i
of D
γ
must obey the relation
d
γ
i
= 1 (6.42)
Therefore, the eigenvalues of P are the γ -root of unity and are given by the
equation
d
i
= exp
j2π ×
i
γ
i = 1, 2, ···, m (6.43)
This proves the theorem. Note that the theorem does not preclude repeated eigen-
values having the same value as long as P can be diagonalized.
Example 6.4 The given transition matrix corresponds to a strongly periodic Markov
chain. Confirm the conclusions of Theorems 6.1, 6.2, and 6.5
P =
⎡
⎢
⎢
⎣
0100
0010
0001
1000
⎤
⎥
⎥
⎦

6.8 Transition Matrix Elements 195
The period of the given matrix is 4 since P
4
= I. Using MATLAB, we find that
the determinant of P is ⌬ =−1. The eigenvalues of P are
λ
1
= 1 = exp
j2π ×
4
4
λ
2
= j = exp
j2π ×
1
4
λ
3
=−j = exp
j2π ×
3
4
λ
4
=−1 = exp
j2π ×
2
4
The matrix can be diagonalized as
P = XDX
−1
where
X =
⎡
⎢
⎢
⎣
0.5 −0.49 −0.11 j −0.49 +0.11 j −0.5
−0.50.11 −0.40 j 0.11 +0.49 j −0.5
0.50.40 +0.11 j 0.49 −0.11 j −0.5
−0.5 −0.11 +0.40 j −0.11 −0.49 j −0
.5
⎤
⎥
⎥
⎦
and
D =
⎡
⎢
⎢
⎣
−10 0 0
0 j 00
00−j 0
0001
⎤
⎥
⎥
⎦
We see that Theorems 6.1, 6.2, and 6.5 are verified.
6.8 Transition Matrix Elements
The following theorem imposes surprising restrictions on the values of the elements
of the transition matrix for a strongly periodic Markov chain.
Theorem 6.6 Let P be the m ×m transition matrix of a Markov chain. The Markov
chain is strongly periodic if and only if the elements of P are all zeros except for m
elements that have 1s arranged such that each column and each row contains only
a single 1 entry in a unique location.
Proof We begin by assuming that the transition matrix P corresponds to a strongly
periodic Markov chain. We proved that P must be unitary which implies that the

196 6 Periodic Markov Chains
rows and columns are orthonormal. This implies that no two rows shall have nonzero
elements at the same location since all elements are nonnegative. Similarly, no two
columns shall have nonzero elements at the same location. This is only possible if
all rows and columns are zero except for a single element at a unique location in
each row or column.
Further, since we are dealing with a Markov matrix, these nonzero elements
should be equal to 1. This completes the first part of the proof.
Now let us assume that the transition matrix P is all zeros except for m elements
that have 1s arranged such that each column and each row of P contains only a
single 1 entry in a unique location.
The unique arrangement of 1s implies that P is column stochastic. The unique
arrangement of 1s also implies that the determinant of P must be ±1. Thus the
product of the eigenvalues of P is given by
i
λ
i
=±1 (6.44)
Since P was proved to be the column stochastic, we have
|
λ
i
|
≤ 1 (6.45)
The above equation together with (6.44) imply that
|
λ
i
|
= 1 (6.46)
Thus we proved that all the eigenvalues of P lie on the unit circle of the complex
plane when P has a unique distribution of 1s among its rows and columns. Accord-
ing to Theorem 6.4, this implies that the Markov chain is strongly periodic. This
proves the theorem.
6.9 Canonic Form for P
A strongly periodic Markov chain will have its m × m transition matrix expressed
in the canonic form
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
000··· 001
100··· 000
010··· 000
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· 000
000··· 100
000··· 010
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(6.47)
