Есин О.А., Гельд П.В. Физическая химия пирометаллургических процессов. Часть 2

Подождите немного. Документ загружается.

лено

тем

[109],

нто

они

разрь1вают

свя3и и

умень1пают ра3мерь|

анионов' например:

_о

о_

\./

,,,

$|\

о о

^-+

0\|

|/о

-о751

,5|\ о

\о/

о_

2Р-

_о-

-о_

_о

_о_.

,|!

го_г

.[,ля

су>кдения

том'

на

какие

анионь1

распадается

трех-

мерная сетка'

больтпое

значение имеет

факт

слабого

умень1ше_

ния

энергии активации

вязкого

течения в

интервале

составов

от 100/9

(или20о|9)

ло

50о7'

Р1е*0.3тими

анионами'

по-видимо-

му'

не

могут

бьтть бесконечнь1е

цепи,

лентьт и

листь1, наблюдае-

мь1е в

кр|тсталл|1ческих

силикатах' Фни

сильно

различаются

по

структуре. |!ри их появлении

следовало

бьт

о>кидать

ре3ких

изменений Ё,

лри содер)каниях

33, 43 и50о|о

]у1е*Ф,.тего

дей-

ствительн|о'сти

не наблюдае}ся.

.&1едленньтй

спад величиньт Ё,,

ука3ь]вает

на

маль1е и

посте-

пеннь1е изменения

структурь1

анионов.

!,>к.

Бокрис

соавто-

рьт

[9!}

полагают, что

интервале составов

от

10%

(20о/о)

до

50о|о

Р1е*Ф

анионь]

представляют собой

постепенно

умень11]аю-

щиеся

<<комочки>>

с общей

формулой

($!"Ф2"".3)6_.

Аргументом

в пользу

такого

строения является

то,

что

в этом случае

угол

ме)кду

свя3ями

в 5|

5! составляет

около 135",

т.

е.

наиболее

6лизок

наблюдаемому

стеклах

(140').

€ут!кство_вание

анал'огичньтх

структур бьтло

обнарух(ено

ранее

Ё.

3. Беловьтм

[110],

нашедш:им

в-

минерале

миларите

1шестичленнь1е

<<двухэта}кнь1е>>

анионь1

(5!:Ф?_)

о.

|!ри_п:^7

(или

6) образ_уются наиболее

кр.упнь1е

<<комоч_

к|1>>

(51э:о!ь

)

илп

(5|9цо!;

на

которь1е

распадается

трехмерная сетка

5!Ф2

при

добавлении

к ней 11-12о|9 !т1е2Ф.

Аналогично при

п:4

появляются

анионь] (5!12Ф!7

отве_

чающие

20о|1

|1еФ'

|1оследовательное

увеличение

содерх(ания

окислов

металла ведет

умень|пению

размера

<<комочка>>

до

200

простого

трехчленного

кольца

513о3-,

что соответствует

не-

прерь|вному

слабому

падению

ё'.

Анион

5!3о3_

на

базе ко_

торого

постр,оень1

вь||пеука3аннь1е

комплексьт,

обнару}|(ен

ре-

11]етках

минералов

бентонита

и волластонита.

Ёа

его сущест-

вование

ра-сплавах

указь|вает

пони}|(ение

точки замерзания

0аР2

п!и

добавлении

маль]х

порший

метасиликата

кальция.

Фно.ока1алось

три

ра3а

мень|пе'

чем

отвечающее

формуле

€а5!@3.

Фтсюда

следует'

-что

метасиликат'

раствор""сь

в'саРэ,

дает

анионь:

5|3Ф

{111].

Ёачиная

509о

-й'*о,

энергия

активации

падает

бь:стрее,

что

мох{ет

бьтть

объяснено

появлением

3начительно

мень11]их

единиц

течения'

а именно'

простейтших

анионов

5|о!_

||о

мне-

нию

1. Боока;[1.11],

интервале

составов

от 50

до

66'6% 11е*Ф

расплаве

имеются

ли1пь

два

сорта

анион,ов:

5|3о

5!Ф!-

поль3у

чего

говорит

почти

прямолинейное

изме-

нение

вя3кости

с составом

Фднако

наличие

небольтцого

максимума

ё,

при

52о|о

]у|еФ

привело

[>к.

Бокриса

и соавторов

[94]

другому

заключению.

(-'ни'полагают'

что

при

добавлении

5|Ф2

к ортосиликату

про-

исходит

обр_азо-вание.линейньтх

цепочечнь]х

анионов

с обйей

формулой

(5|"о3'+')(2п+2)

3аметное

увеличение

единиць|

течения

от

51@|-

к 5!2@!-

5-;'о?ы

т.

д.

вь]3ь1вает

относительн'о,

бь:стрь:*

подъем

ё'.

€

известной

длиньу

цепи

становятся

менее

устойнивьтми,

чем

кольца'

4_п^ер9ходят

в них.

Ёаибольтпая

длина

цепи

достигает_

:т дву

520|о

|1еФ,

когда

линейньтй

анион

имеет'

формулу

)|'096'_.

||ри

этом

х{е

составе

энергия

активации

вязкого

течения

становится

максимальной.

3атем

цепи

превращаются

кольца

5|3о3_

мень1пего

ра3мера

величина

?'..й''"*'

пони)кается

|!ри

температурах

вы|пе

1700"с энергия

активации

вязко-

гс

течения

становится

мень[пе

у расплавов

€аФ

5!Ф2

всех

!|зученнь1х

составов.

Бозмох{но,

что

усиленнь1е

тепловь1е

коле-

бания

ослабляют

связи

о,

что приводит

к частичному

распаду

комплекснь|х

анионов

на

более

прость1е

и легко теку_

щие.

9мень1пение

величинь|

Ё1 с 7

ограничивает

применимость

простейтпего

уравнения

(!|!,

18).

Фпь:т

пока3ь!вает

(см.

табл.'8),

нто

для

одновалентнь1х

ка-

тион0в

Ё,

падает

(при

330/9_45016

||е2Ф)

увеличением

кул,о-

новского

притях(ения

их

к аниону

кпслорода (|)'

€ледова-

тельно,

тормозит

вя3кое

течение не

свя3ь

катионов с аниона-

ми'

стерические

3а"руднения.9ем

более

ра3мер

катиона'

тем

201

больш_тие силь1 отталкивания

испь1ть1вает

он при перемещении

и тем

больтпе

при

равных

условиях

велинина

ё'.

|(огда концентрация

одновалентнь|х

кати'о'нов невелика

(15-20у0

]у1еэФ)'

стерические

затруднения

становятся

мало

существеннь1ми

по сравнению

с таковь1ми

для

анионов. 3

этих

условиях

Ё'практинески

перестает

3ависеть от-природьт

ка-

тиона.

|1ри'одном

и том

х(е мольном

проценте

Р[е*Ф концен-

трация

двухвалентнь]х

катионов

два

раза

меньше' чем

одно-

Рис.

73.

3ависимость

вязкости

шлаков

системн

€аФ

5!о2

А1203 от

состава

при 1900'6

валентнь]х.

|!оэтому

стерические

трудности

при

их

перемеще_

нии могут бь:ть обЁару>кены

только

при

концёнтраши{х

!т1е*0

больтпих,

чем

изученнь:е

(}450/6

|4еФ).

||ри

добавлении

йе'Ф

51@2

сильно

ц3щецяет9я

прецэкс-

понейциальньтй

мно)китель

уравнения

(|1|'18)

[ля

обсух<-

дения

этого вопроса

Ах<.

Бокрис

и соавторь|

[94]

используют

теорию

переходного состояния'

согласно

когорой

ц:+*,{#}*,{+}.

(11т

24)

3десь

число Авогадро,

!а

постоянная

|1ланка,

молярнь:й

объем

единицы

тёнения,

А$*

энтропия

актива_

шии.

.(опустив

плотную

упаковку

атомов

кислорода'

они

под_

считали

для

вышеуказанных

единиц

течения

(настиш

5|Ф2

2о2

203

дискретнь|х

анионов).

3ная !,

||,!

Ё,

они

оценили

А$*

по

уравнению

(11|'24).

||ри

этом

ока3алось'

что

для

чистой

двуокиси

кремния

^5*

20.

3десь,

как

в'оды,

А5*

боль-

!пая

полох(ительная

величина.

Б воде'единицей

течения

яв_

ляется

молекула

Ё2Ф.

Фбразование'

переходного

состояния

сопрово>кдается

ра3рь|вом

ряда

водороднь]х

связей,

вследствие

чего

энтролия

в этом

состоянии (5*)

больтше,

чем

началь-

ном

(5).

Аналогично

вя3кое

течение

5!Ф2

'ак>ке

сопровох(_

дается

ра3рь]вом

сравнительно

прочнь|х

связей

о,

чем

фсл

о'влен

поло'{ител

ьньтй

н а

к энтр

о л\1\4

акт|4в

ацит4.

||ри

добавлен\4и

окисл,ов

металлов

величина

А5*

резко

падает

к-отрицательнь|м

3начениям.

Ёачиная

х<е

с 100/о /т1е2Ф

и 20!о

||!еФ

уцзменения

энтро[1н\4

акт11вации

становятся

маль|-

{1^

Б этих

условиях

едини!дей

течения

являются

не

частиць{

51Фэ,

а,

Аискретнь1е

анионьт.

|1ереходное

состояние

для

них

ока3ь]вается

менее

вероятнь]м'

чем

исходное'

величина

А5*

приобретает

отрицательнь:й

знак.

1(роме

-того'

двухвалентнь]е

(3!1!Ф:ЁБ1

'обладают большой

долей

,ковалентной

сЁязи

обра-

уют

<<м

ости'ки)>

м е)кду

а н,и,он

м,и. Бол

ее

упорядо'чен

на

ястр

ук-

тура

умень1пает

энтропию

исходного

состояння,

6лаго'даря

че-

му

А5*

становится

3десь

менее

,отрицательной,

чем

у''Ёй'''-

лентнь1х

катионов.

}*"ч.^образом,

исследование

бинарнь:х

расплавов

$е*о

5|о2

показь1вает'

что

'вя3кость

их определяется

глав-

ньтм

образом

ра3мерами

и структурой

компйекснь:х

анионов

отчасти

энергией

интерионного

в3аимодействия

!{е2+

и Ф2-.

Бязкость

системь1

с9.9^_

Аьо3_5|о2

и3учалась

р'л'*

авторов

(см.,

например

[112]).

последние

годь|

она

тщатель_

но

про^мерена

интервале

1600-2100.с

[113].

(ак

видн,о

из

рис.

73,

лин|1|1

равной

вязкост].| (из-окомь!)

имеют

'о."у''.',,

которая

отвечает

отнотпению

€аФ75|Фэ

1. |1о_вилимойу,

та-

кой

ход

и3оком

обусловлен

и3менением

координаци|1

иона

А1'*,].

е. амфотерйостью

глино3ема.

основных

*''*'"

А1!1,

подобно

крем}|ию,

окрух(ен

четырьмя

анионами

кислорода'

'в

кисльтх-

1пестью.

3тодоятверх(дается

так}|(е

максимумом

энергии

активации

при

€аФ/51о2

!!.

Бязкость

(ц)

х<илкогю'глнно3ема

при

2100.€

ока3алась

сравнительно

небольтшой_0,5

пз. Ёапротив,

поверхностное

натя)кение^(9)

окиси

алюминия

достат0_чно велико

[!:з]

со-

ставляет

650 эре.см-2.

1акое

сочетание

малой-

вя]кости

оольшого

натя)|(ения

свойственно

жидкостям

ионныйи

связя.ми'

например

]ч1а€|.

Ёапротив,

окислы

со

3начительпой

долей

ковалентной

связи,

напринер

5'о2.в2о3,

обьтчно

обла.

дают большей

и мень1пим

{]:з].'

3язкость

и3вестково-глино3емисть1х

расплав,ов

исследова-

лась

так}ке

А.

11]алам0вь1м

[. 1(уколевьтм

[114].

€огласно

и.

|ультяй

соавторам

15]

о'кись

калия

ло-

вьт|:]ает велини,у

системе

€аФ-А1эФ1--

1$1-Фэ_

особенно

основнь|х

шлаках.8близи

состава'

гАе

9о€аФ|оБ9|о'-.|,

цд$дрдается

минимум

ц.

Богатьтй

экспериментальньтй_мате-

оиал бьтл

получен

по влиянию

на вязкость

расплавов

€аФ

йво-5!Ф2

глинозема

т[115],

а таюке

окиси

6ария

маг-

ния

16].

||ри

этом

оказалось'

что п-ри

постоянном

отно1шении

сао7з;6,

"ё'",'"а

в системе

6аФ-&1вФ-51о2

ростом

содерх(ания

}19Ф проходит

через

максимум'

а в

расплавах

€аФ^-

БаФ

5|о, с повь11пением

количества

БаФ

чере3

ми-

нимум

[116].

Авторьт

свя3ь!вают

это с

различнь1м

размером

*омйлейсов

5!"ог

катионов

.]!18'* и

Ба2+.

Бязкость

систе-

мь1

1у1пФ

5|о;

А12о3

и3учалась

ш.

м.

}1икиаш:вили

и соавторами

[117].

Ами о6нару)кен

ми*нимум

для

состава

700/9

}1пФ и 300/о 5|Фэ,

гАе отн'о'1шениео/51:4

присутствуют

простейтшие

ионь1

5'о

.[обавка

$!@э и

А1эФз

ведет

укруп_

Рие. 74.

3ависимость энер-

ги}1 акт|ивации и вязкости

от состава

расплава

|'{а:Ф. 35|Фэ

РеФ

Ре2Ф3

нению

комплекснь1х

анионов

повь1шению

ц.

Фтметим,

что

вязкость

гли-

ноземно-титанисть]х

11]лаков

исследовалась

€.

А.

(унильни-

ковь1м

соавторами

[118]'

даннь1е

для

систем

€аФ

!:Фь,

}19Ф

!яФь,

Рьо

!эФь

других

бьтли

получень|

Б. .[!. 3язевьтм

'119].

Ёа

рис.

74 п'риведеньт

ре-

3ультать1

измерений

Б.

-[.-(ор-

пачева

соавторов

[103].

3десь

вя3кость

системе

}']а:Ф'

.35;о2

РеФ

Ре2Ф3

сних{а_

ется

при

увеличении

содер)ка_

ния

0кислов

х(елеза

сперва

силь'но

(ло

35о/,

РеФ

Ре2Ф3),

?,соо.

|гзоо"

/,6

0,0

?01

!чЁ

'г

со

|;}-]-со

;' !

о0

(|е0,гер')'%/гсол)

а 3атем

медл,еннее.

Бол,ее

резкий

п'ерело'м

примерно

!пр'и

том

х(е

,соста|ве

имеет кр,ивая

!ля

энерпии

активации.

€казанн'ое

свидетельствует

о существеннь1х

изменениях

строении

рас-

плава

при

переходе

от силиката

на-трия

к окислам

}келеза'

Бслй

оценить

по

уравнению

[120]

од:0,63(+)"|':!тРл

201

{7,

ккол/гтоль

объем

радиус

дь|рок'

возникающих при плавлении' то

их

величинь1

для

всех

ука3анных

11а

рис.

74 составов ока3ь|ваются

блуазкими

(,,.:

1,49-|,24

А)

ра3мерам

ио'на

кислоРоАа Ф2-

|,32 А).

Бсли

предполо>кить' что вся

энергия

активацт,!и

расхолуется

только

на

образование вакансий, т. е.

Ё,

Ё'

:4'г2д',

(где

Ёд-энергия

образования

дь]рки'

о-поверхностное

натяжение),

то по

опь1тнь1м

значениям

Ё' (переснитанньтм

на

одну настицу)

о'

мох(н,о

найти

радиусь|

дь|рок'

необхо.

димь|х

для

вя3кого

течения.

[ля

1400"€

они

имеют 3на-

чения' приведеннь|е

в табл.9.

9 последних

трех соста-

вов

3Ёачения

г 6лизки

к ве-

личинам

гд.

|1о-видимому,

расплавах'

содер}кащих

менее

50%

51о2,

единицами

течения

являются

одноатом-

ньте

ионь1.

Бероятно,

3десь'

?аблица

Р!д!у(ы

днрок,

нео6ходиино

для

вя'кого

точэ!.'я

11,0

53,5

2,57

48,8

2,48

39,6

1,90

20,8

1,53

1,47

1,26

как

неасооциированнь]х

х<идкостей'

величинь| Ё!

опрелеляются

основном

энергией

образо'вания

дь:рок

Ё'.

расплавах

с концентРа(ией

двуокиси

кремния

более

500/9'

зна'чения

превь|1пают

гд,

расхо)кдение

мех{ду ними

увели_

чивается

вместе

содерх(анием

5!Фэ. Фневидно,

11ач||ная

с этих

концентраций

51Ф:,

доминирующая

роль

в определении

свойств

расплава

переходит

к }кестким

свя3ям 5|

5!.

/\идкостьстановится

достаточно

сильно

ассоциированной,

величина

Ё,

больше Ё^.

Аополнительная

3атрата

энергии

Ёп: (Б;-Ё*)

мох(ет

бьтть

обусловлена

двумя

причинами:

увеличением

размер'ов

еди.ниць1

вязкого

течения

усилением

прочности

связи

ее

окру}|{ающими

частицами.

Бсли

бьт

имела

место

только

пер-

вая

причина'

то вь1численные

радиусьт

дь1рок

были бьт недо_

статочнь|ми,

чтобьл

целиком

вместить

кремнекислороднь1е

к,омплексь1

указь]ваемьтх

литературе

размеров

(г)3

А).

\онечно' не

исключена

во3мох{ность'

что

некоторь!е

из

комп-

лексов'

например

линейнь:е,

осуществляют

вя3кое течение

(подобно

полимерам

длиннь]ми

цепями) отдельнь1ми

сегмен-

тами.

Рсли

допустить'

что

основн,ой

является

вторая причина'

то

единиць1

течения

останутся

небольшими,

дополнительнь|е

,'"'

[

.,',,

3атраты

энергии

(Б")

булут обусловлень:

необходимостью

растягивать

да)ке

обрь:вать

некоторь1е из связей 51

$1,

что6ьт единица

течения

могла переместиться

ва-

кансию.

Бязкость

)кидкости

умень1шается

ростом

свободного

объ-

ема

числа

(п)

ъакантнь|х мест. Белинину

/}}

мо)кно оценить

по

прират'{ению

объема Ао при плавлении:

Б,

|)д

Беря приблих<енно

Ао

равнь:м ра3ности

объем,ов при

1400

ут 20'

находим'

что

значе({ие

для

с||л|тката

натрия

(0,35.

1023)

понти

на

порядок величинь1

мень1пе'

чем

у,окислов

}|{елеза

(3,36.

|023

тлтук|моль).

1аким образом,

резкое

падение вязкости и

энергии акти-

вации

при

переходе от силиката

ъ1атр|1я

г\а2Ф.3$!о2

к окислам

)келеза мох(ет бьтть пояснено значительнь]м

увеличением

чис-

ла

дь|рок

х(идкости и

умень1пением

числа направленнь1х

связей.

!]иффу3ия

подв]||шнооть

]|онов

в ц|лаке

Аля

определения

коэффишиентов

диффузпи

(Р)

в окислах

1плаках

применялись

различнь1е

методь1' обзор которь|х

дан'

например' 8. [4.

.д}1алкинь1м

и Б. .&1. !!1огутновь1м

[|2\),

такх{е

Ё{. €. [орбуновь|м

и 9. А. йзвековьтм

т[122].

Аля

расплавов

наибольтпее

распространение

получил метод

капилляра

(п,о_

давление

конвекции)

в сочетании

радиои3отопами.

1ак,

,[,х<.

9'и,пман

[1'23]

соавторь1

,и3учали

при

температурах

1350-1450'€

распределение

изотопа

€а{5

по сечению

11|лака'

содерх{ащего

40$

€аФ,400/о

5|Ф2

и 20%

51о2.

3начения 26д,

вБ|т|[€леннь]е по и3менению концентрации

и3отопа

вдоль

центральной

осн,_оказались

рав,нь1ми'

напри-

мер, 3,3

\0-т

см2. сек-|

при 1350'6, а энергия активацип Ё

70г*

ккал|е-атом.

*1а!гденнь1е величинь:

бь:ли

подтвер}|(_

день]

по3днее

Ёибо{4

[|24|'

однако

его

даннь|е

для

сильно

расходятся

для

6лизкпх

составов.

1ак,

1шлака

из 409о €аФ,

407о $|@:

и20оБ

А1эФз

значения

Рс^

п Ё

составляют

3,3.

\0-7

см2.

сек-|

ккал|е-ато]]4'

то время

как

для

расплава

с 430|1 €аФ,

390/9

5|Фэ

18% А12о3 они

соответственн,о

равнь|

5,2.

\0_7

см2.

сек-|

и 30

ккал|е-атом' Б

более

ранней

работе

других

авторов

так}|(е

получена энергия

активации

не 70,

а 29 ккал|е-атом. |1ри

этом,

'однако'

коэффишиенты

диффузии

206

2о7

(в

тшлаке с

37'50Б

€аФ,52,5о|о

5|Фэ

100/0

А!2о3)

бьтли вь:тпе,

"менно

9,6.

10_6 см2.

сек-1

(при

1450" €).

|1олагая,

что электричество

в исследованном

шлаке

пере-

носится

ли1пь

катионайи

кальция'

А>к.

9ипман

соавто_

рь:

[123]

вы.числяют

'по

коэффишиенту

9ч

уравнению

Ёернстй-эантптейна

сначала

подвих(ность

(ш)

ттона:.

2ео

ы'-

нт

по

ней

удельную

электропроводность

х 1шлака:

|.|2

.|0'

"о

'т

3десь

Ё_константа

Больцмана,

€-элементарнь:й

заряд'

2-вале11'|ность'

.а с-концентрация

(нисло ионов

\ см3),

||ри

1450'€

раснет

дает

х:

0-,0-6]-

ом-|'см-1'

то_

время

как

экспериментально

найденная

[125]

велин11!1а

х:

0,098.

}чить:_

вая ойибки

измерений

их,

так-х(е

прибли>кенность

(о

при_

менимо,сти

уравн'ения

Ёернста

3йнштейна

см.

них<е)

вы_

тисл'ений, мох(но'считать

с'огласие

вел'ичин

пр'о'водим'ости

удо'вл

етво'р ител.ьн

ь|м.

в. с.

31ронйов и

соавторьт

[126]

обнарух{или

наряду

9:б"-

емной

еще

й поверхност"ук!

лФФтзию

6а+ь

1плаках с 39,4?о

€аФ,

38,80/9

5!Фэ и

2\,20|о

А12о3.

Б графитовь1х

тиглях' не

сма-

чиваемь|х

расплавом'

коэффишиент

!6"

(вь:нисленньтй

по

кон_

центра1{иям

€а{5,

усреАне}!ньтм

по сечениям'

перпендикуляр-

нь]м

н.аправлению

дффузии)

бьтл

на порядок

величиньт

боль-

ше,

чем

в корунди3овь]х

трубках,

хоро1по

смачивающихся

|плаком.

Б последнем

случае

найденньте 3начения

|4'

6лттзкп

полученнь!м

другими

авторами

(табл.

10).

@днако энергия

1аблица 10

хо'.рф!цх.нтч

диффу'хи

1с;вэ'сетс_|

'о|ов

п!п}цх'

.}осфоР.

Р!сп'!в!'

€а@

А|1@9

51Ф9

|р

[126]

Бс,

1|26) !1

231

ос

1300

1350

1400

1450

1 500

1540

(8-12).10-7

(1,4+2,5).10-6

4,5.10-6

4,4.

10-6

(3,1-5,6).10-7

(0,9-

,8).

10-6

2,4.10-6

3,8.10-6

3,5.10-7

0,68.!0г-6

|,3.10-6

2,1. 10-6

3,4.10-6

зцтивации

(€6')

них<е,

нем в

работах

[123]

и составляет

56,6

ккал|е-атом,

что согласуется

с величиной .8о"

ккал|е-

атом,

найденной

работе

[\27]

для

основнь|х

|шлаков.

Расчет

.Р6д

по

даннь1м

[\25]

для

электропроводности

(х:

:0,!29

ом-|.см-|

для

1450:€

и состава

45о|о €аФ,

350/9 5|@2

|9оА

А12о3) с помощью

уравнения

Ёернста-3йнтлтейна

при_

водит

к 3начению

Р^

,-:

'9:ч"

:2,5.

1г6

см'.

сек-1

€а.|

Р2э2с

очець близкому

непосредственно

и3меренному

(2,4.

10_6).

Бесьма

примечательнь1м

является то

обстоятельство,

что

коэффишиент

Аиффузии

фосфора

не

мень1пе' чем

кальция.

1' ц.

самое

бьтло полунено

для

расплава,

содер'{ащего

30%

€аФ

70о|9

Р2Ф5

при

температурах

980-1000'с

[12в].9тобь:

убедиться,

что

близость

коэффициентов

|р

|44

не

вьтзвана

конвекционнь|ми

помехами'

и3мерения

производились

[128]

ни'(е

точки плавления (750-800'€)

течение 200_250

в стеклообразном

состоянии.

1(ак видно

и3

даннь|х

табл.

!1,.

величинь1

|р

|1а

остались

близкими

и в случае

полного

устранения

конвекции.

1аблица

ко'ффхц'.п'ш

лхффуз|х

фосфоР!

х к.'}ц'я

1(оэфпциент

диффузии

температура'

ос

750-800

оР

|с^

(4,3-6,7).!0-8

(3,1-4,6).10-8

(2,6_2,7).1о_6

(3,0-5,0).10-6

6казацное

подтвер}кдает'

что

фосфор

Аиффундиру9т

в 1плаках

не

виде

сло)кного

комплексного

аниона. 3то

согла-

суется

с его

перемещением

к катоду

при электролизе

[м].

Бо_

лее того'

полученнь]е

даннь1е

приводят

к правильному

3наче-

нию электр опроводности.

!,ействительно'

.{подвих(но'сть,иона

кальция

|с.2+,

рас-

считанная по смещению

изотопа €а{5 под

действием

электри-

ческого поля' составляет

8. 10-5

см2.

в-|.

сек-|

!,ля

1плака

307о €аФ и

700ь

Р2о6

при

1150'с

[64].

€

унетом

числа

пере-

11оса пса2+ это

дает

подви>кность

фосфора,

!авн}ю

ир:

3,4. 10-5

см2

в-|

'.^сек-|.

Фтсюда

удельная

электропровод_

ность

|'плака

х:0,16 ол_1

.см-|,

что

мало

отличается

от

непо.

средственно

измеренной

величиньт

х:0, 168

ол_1

см-1

Боль.

тшой

коэффициент

лиффузии

фосфора

вь|зь|вает

удивление'

так как

!51

согла€но

[123],

Аесйть

раз

меньтпе, нем-!6д.

.[|,иф_

фузия

€а{5

расплавах

6аФ

5!Фэ,_€аФ

А12Ф3,

€аФ.51@'-

А|2о3 и- €аФ

А12о3

5!о2

&1вФ

исследовалась

также в

ра-

6отах

[!27].

|1олуненнь|е

ре3ультатьт

близки

к вь:1пеприведен-

ньтм. |1орядок

величин

'са

ле)кит

пределах 10-6_[0_7

см2.

сек-|,

значения

энергии

активации

колеблются от 40

до

ккал|е-атом.

.(ерги

и соавторь!

[123]

определили

методом

капилляра

с помощью

радиои3отоп4

А126

коэффициентьт

самолиффузии

алюминия

расплавах

€а@

А12о3

5!о2.

Фни натллй,

нто

для

|плака

соста'ва 47,2о|о

(а@,47о|9

5!Ф2

и 60/о А12о3

величи_

на

!)д1

опись1вается вь!рах(ением

ьт

:4,3

104

ехр

850Ф7(?},

а-

д!я

Рас_цл1в1

с ббльтпим

содер>канием

глинозема

(43,80/0

€аФ,47,30|9

5|Ф2

|2,5оь

А1эФз):_

0.,

:5,4.

10д

ехр

60000/&г}.

|1ри

этом

3начение

.}.1з+

10-7 см2

сек-| (при

1450'с)

мень11]е'

нем

|""э1

1,3. 10-6,

но

несколько

боль_

1пе,

чем

4.'

!,2.

!0-7

,''. ,''_т

у\23!'

1акое

расп'оло}кение

величин

соответствует

доле

ковалентности

связях

!у|е

она возрастает

РяА}

€а, А1,

51.

Амфотерно9т1-

А!эФз

проявляется

в том'

что с

увеличением

отно1пения

€аФ/А1э@з

растет

Аоля

ионов А13+,

}1аходящаяся

|пестерной

координации.

3то

приводит

к повь]1пению

их

подви)кности,

следовательно'

коэффишиента

лиффузии

уьт3*

3начения

этих

велич14н

для

€аФ/51Фэ:

и 1450.с

приведень1

табл' 12.

1аблица

значэняя |,* н

т1

р.спп.в.х

сао-А|?о'_5!о2

при

6а@/5!@2-1

1450о-с

ь\'о",

|о

о.!0?'

с'12,сек

пв

12,5

6,0

0,1

0, !5

Ёстественно'

что

при

этом

уменьшается

Ёя3кость,

так как

происходит

ра3укрупнение

крем1{еалюмокислороднь|х

(Фй|!.

л_ексов'

т.

е.

поних(ение

числа

)|(естких'

ковале!|тнь|х связей.

Ёапротив,

электропроводность'

3ависящая

главнь1м

образом

от

,подвих(ности

числа

катионов

€а2*

повьттпается.

Аля

полнотьт

информации

лиффузии

ионов в

системе

6аФ

51о2

А1эФз

необходимо

бь:ло,

кроме коэффицие-нтов

|с^,

|ьт

б., оценить

еше

09.

Аля

этой

цели

в-

-_работе

[129}

исп'ользовались

стабильнь1е

и3отопь1

кислорода:

9:т

6:в.

1(он-

центрации

их

определялись

помощью

масс-спектрометра

газовой

фазе,

полученной

вос-

становлением

отдельнь1х

участ-

ков

!шлака

графитом.

14змере-

ния пока3али'

что

коэффишиент

лиффузии

кислорода

весьма

велик

(10-12.

10_6

см2.

сек_|

лрп

1475" 6)

превосходит

да-

>ке таковой

для

кальция.

||одобньте

х(е

ре3ультать|

бьтли

найдень|

другой

работе

[130]

при и3учении

скоро-

сти

растворения

пу3ь1рьков

кислорода

расплавленнь1х

стеклах

(например,

Р62_

\,4-2'5. 10-6 см2

сек_| лрп

1300" с).

Рис.

75.

€опоставление

коэффиши-

}(оэффишиентьт

лиффузии

ентов

диффу3ии

кислорода'

каль-

стаоильнь1х

изотопов

могут

ция'

серы'

алюминия,

фосфора

бьтть представлень1

[129]

сле-

'кремния

'(идких

1шлаках

дующими

уравнениями:

|6тт

3,73

105 ехр

85000/&т}

Р9:з:{,$$.105ехр{*850ф/кг}'

и3 которь]х.следует,

что энергия

активации

этом

случае

весьма

велика.

Ёа

рис.

75 оопоставленьт значения

коэффишиентов

для

ионов €а, А1, 5! и Ф, а такх{е

для

[126]

[131].

то время

как прямь1е

19 2, 7-|

располагаются

для

и,о,нов €а, 5, А1

в соответствии с их

размерами

долей

ковалентности

связей

[у1е_ Ф, поло>кение

прямь1х

для

кислорода

фосфора

ках(ет-

ся неох(иданнь1м.

€ледует

заметить'

что

коэффициенть1

|о, |с1'

Рд1

|3у

определеннь|е

с помощью

и3отопов

расплаве

6аФ

А1эФз

5|@2, могут

бь:ть названь|

коэффишиентами самодиффу3ии

ионов

Р''.

Б этом случае

ион

дви)кется

,в

среде'

которой все

остальнь|е'

]-ионь:

не

имеют направленных перемещений,

так

как

градиенты

концентраций

для

них отсутствуют. Беличина

2{0

2'1

Р]

пропорциональна

поэтому

квадрату

смещения

единицу

времени

при беспорядо,чном

тепловом

дви}(ении

иона

яв_

ляется

характеристикой

его в

данной

среде

при

-фиксирован_

ной

темпщатур-е.

|{ри

диффу3ии'

например'

€а{5

в €а@

А1эФз

5|о2

происходит

простой

обмен

местами

ме}кду

иона-

ми

радиоактивного

стабильного

и3отопов.

Ёапротив,

случае

электропроводности

дви)кение

иона

[

происходит

среде,

которой и

другие

ионь:

]

могут

пере-

мещаться.

Б этом случае

создается

не один'

а !1есколько

пото_

ков

частиц, которь1е

могут

ока3ь1вать

влияние

друг

на

друга.

Б связи с этим

уравнение

Ёернста

3йнтштейна' связь1вающее

коэффишиенть|

самодиффузии

ионов с их подви>кностями

или

электропроводностью

мох(ет стать

несправедливь|щ.

Аействи-

тельно' как показали

Ах<.

Бокрис

соавторь1

[132],

вьтпислен-

ная по коэффишиентам

самодиффузии

ионов

()ш"*

1,53

.\0_ц

см2.

сек-|

|сл_

0,83

.\0-+

см2.

сек-|) сумма

их

подви)кностей в

расплавленной

;\1а€1

(при

935" с) 3аметно

вьтгше

[(2,27

-р

0,05)

,\0_3

см2.

сек_|

в-!|,

найденной

непосред-

ственнь1ми

и3мерениямп

(\,62.

10-3 см2

сек-|

а*').

Авторьт

объясняют

это тем,

что

лиффузия

включает

еще

совместное

перемещение

пар ионов \а+'€1-,

которь1е' естест-

венно'

не

участвуют

в электропр'оводности.

||оэтому в коэф-

фициентьт

самодиффузип

|* входит не

только

величина, от1!о-

сящаяся к

подви}кности

иона

(|1

или

|_\,

но еще и

слагае-

мое,

обусловленное

перемеще1{ием

парь1 ]'{а+ и

€1-, т. е.

)$^*

:}*"+

!*"+.",-; 2",-: Р",-

р*'+.",-'

,0Б9,3;|1

с'о

,сказан,нь|м

ура1внен'ие

Ё,ернста

9й,нш:тейна

следует п,одставлять

не коаффициент

|*',

велин,ину .01, т. е.

}ш"с|-${о""**)",_)'

3ная

!{ }шас:

можн0

оценить

все три коэффишиента

Аиффузии'

которь1е

этом

случае

ока3ались

равнь]ми:

0*"*:

1,19' 10_4;

Р",,,_:0,49'

10_{ и

2ш"с:

:0,34

10-4

с'Р

сек_|.

|!озднее

подобньте

результаты

бьтли

[133]

уточнень|

полу_

чень1

не

только

для

}.{а€1,

но и

для

пьс1,

€в€1,

}',[а.}'

1олько

расплавленном

,}ч[а.!

величиной

}ша"т мох{но

пренебрень;

во

всех

осталь[{ь|х

случаях

она бь:ла

достаточно

заметной.

Бос'

поль3овав1пись

термодинамикой

необратимь1х

(стационарнь:х)

процессов,

Р.

[\айти

[134]

показал'

что при

известнь1х

допу-

щениях

велинина

},;,

характери3ующая

электропроводность

ионов

расплавленттой

соли, мох(ет

бьтть представлена

вь|ра-

жением

'л.1/Р2

а'[,,-

[,',

котором

коэффициент

[;;

свя3ан с

<диффу3ионной>>

подви)к_

ностью

иона

(т.

е.

параметР

|,сэ

учить1вает

изменения

этой

подви}кности

вследствие

п,отока противополох(но

3аря-

}кен}1ь1х

ионов. 8 частности,

для

}:{а€1

при

800" с эти

коэффи-

циенть1

равнь|:

[++

13,5.

10-9,

[_-

6,1

10-9

|-+-: 2,6-

|0-9

моль.

см2.0эю-|

сек_|.

?аким

образом, причинь1

отклонения

от

уравнения

Ёерн-

ста

9йнш:тейна,

во,обше гов,оря'

могут бьтть

разньте

(лиф-

фузия

'ио'нной

|парьт'

1взаимное

1влияние

п'отоков

'и

т.

:п.).

.[|.

9нг

и [.

.(ерги

[135]

склоннь1

полагать'

что в

расплав-

леннь|х силикатах и

1плаках

так>ке следует ох(идать

ра3лич-

нь]е механизмь1

для

лиффузии

электропров,одности. €

этим

различием

они свя3ь|вают' в

частности' несовпадение энергии

ак'г14ваци|4 проводимости

диффузии'

вь1численнь!х

измерен-

нь1х

величи11 х'

а так>ке больгпой коэффишиент

иона

кисло-

рода.

Ёе

исключена' однако'

во3мох(ность' что значительная

вя3-

кость

1плаков' а так}(е

нередко

их

униполярная

проводимость

сильно

уменъ1пают

влия1{ие

других

потоков на

данньтй

по3во-

ляют

тем

самь1м применять

уравнение

Ёернста

3йнш:тейна

ним с больп:ей точностью'

чем

расплавленнь1м

соля1\1.

Аействительно'

согласно

Б. 14.

&1алкину и Б. .|!1. !!1огутно-

ву

[136]'

коэффициент самолиффузии

натрия

в вязком

(ц

125 пз)

расплаве

1.{а2Ф.25|о2 опись1вается

в интервале

температур

970-1210"

€

уравнением

1€0*'*

:2,74-

||ри

этом

энергия активации

диффузии

Ёо:

||,9 ккал|е-

атом хорогг]о

согласуется с

полученной

[68]

для

электропро_

водности

Ё"

\2,0

ккал/е-атом, а коэффициент 2ш"+,

вы-

численньтй

для

1473"

€

по

уравнению

Р{ернста-3йнп_ттейна

},&1

|{а

аРэ

весьма

близок

(2ш,+

3,6.

\0-5 см2.

сек-\\,

эксперимен-

тально найденному

$'2+.

10_5).

3то

позволило

авторам

сде-

лать

вь1вод о тох<дестве|{ности

механизмов

лиффузии

и про-

водимости

ионов !.{а+

расплаве

1.,1аэФ.251о2.

1очно так

>ке коэффициенть|

самодиффузии

ионов }келеза

расплавах

РеФ

5'о2

(насьтщеннь:х

5|Ф2)'

вь1численньте[65]

и| подви;кности

Ре2+

по

формуле

Ёернста

3йн:.птейна'

для

1250"

составляют

0г"

5,8.

10_5 см2

сек-|' т. е.

не

сильно

отличаются от непосредственно

[135]

и3мереннь1х

(|г":

7,9

10-5).

€казанное мох(ет

слу)к.ить

оправданием

для

расчета

ко-

эфф'ишиента

лиффузии

|с^у+

по

данньтм

электро,про|водн'ости'и

чисел

переноса

01^2+,

которьтй

бьтл предпринят

п. п.

Булни-

ковь1м

и соавторами

[137].

Более того' они получили при

час-

тичной

заме}{е €аФ

на БаФ в

расплавах

|1з 54,850/о 6аФ,

22,85о|о

А12о3,

16,60/0

РеэФз

и 6,160/о 51Фэ

максимум

для

|662*

тлри

1,00[ БаФ и температурах

1330-1480"с, что отвечает

максимуму

вязкости.

€ледует, однако. 3аметить,

что

связь

коэффишиентов

диф-

фузии

с величинами

вязкости

(ц)

в силикатах мо)кет

не

под-

ч,иняться

зак,ону €токса. 1ак как

э}{ергия активации

(д

)

проводимости

больгпе' чем

вязкого течения' то

величина

формуле

}}'.ц:€Ф[51

больтпе

единиць|. ||оскольку

3начения

Р и ?,, согласно

урав-

нению

Ёернста

3йнтптейна' пропорциональнь{

друг другу'

то

о,

ч:

€Фг151:.

Аругими

словами'

коэффишиент

диффузии

обратно

про-

порционален

не первой

степени вя3кости,

как это требует

закон

€токса:

-ьт

о_

|(роме того' величина

ра3личнь|х

ионов.

14звестнь:м

подтвер)кдением

сказанному мо'{ет

слу)кить

табл.

13,

в которой помещень|

даннь1е

Р.

€.

3оронцова

[13;

133]

для

коэффициентов

лиффузии

Р,

€а, $ и

Ре

в |плаках'

содер)кащих

40-43%

€аФ,

210/о

А1эФз

и 35-33%

5!Фэ. 3десь

прои3ведение

|г

,о'ста,ется

|постоян'нь]м

только

для

'ионов

Ре2+

(а2*,

уко,торь1х'вел'ич'инь1

г,соответств,енн,о

6лцзки

друг

другу.

||ри

заметном

и3менении

ра3мера

иона'

напри-

мер'

при переходе

от €а2+ к

52_ коэффициеят

| меняется

слабо,

произведенпе |г

оказьтвается переменнь1м.

Аналогичньте

ре3ультатьт

бьтли

получень1

А.

Б. Банюковь]м

и Р1.

./!1онтильо

[139]

для

1плаков с

39,90/9

5|Ф2,

2|о|9

(аФ,

19,1?0

РеФ,

9,8?о

А1эФз

10,2о|9

.]!1вФ.

21,

апг!|

мох{ет бьтть неодинаковой

для

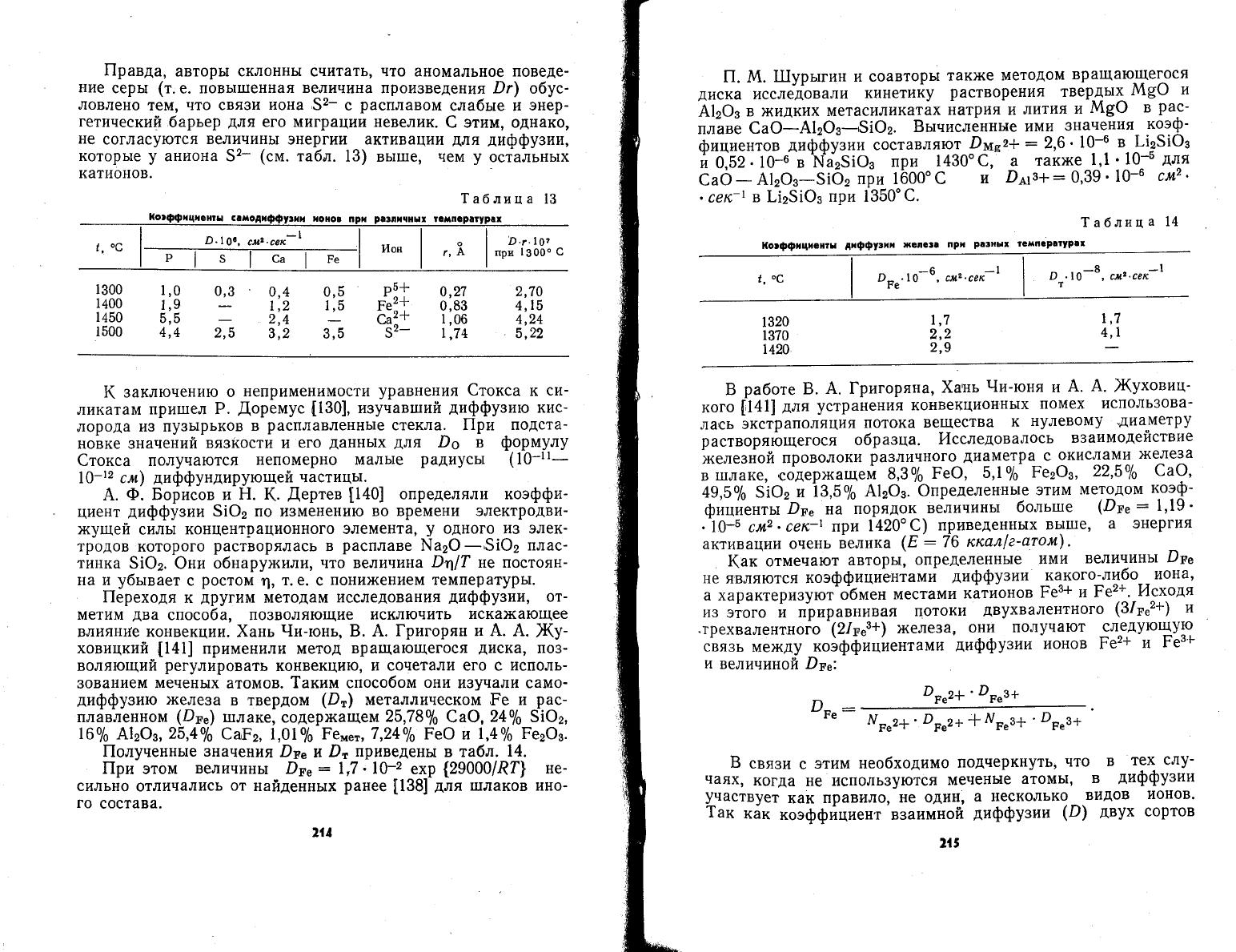
|!равда,

авторь1 склоннь1 считать' что аномальное поведе_

ние

серь1

(т.

е.

повьттпенная

величина

произведения

Рг) обус-

ловлено

тем'

что свя3и

иона

52_

расплавом

слабьте и

энер-

гетический

барьер

для

его миграции невелик.

6 этим, однако'

не

согласуются

величинь1

энергии активаци||

\ля

лиффузии,

которь1е

аниона 5:*

(см.

табл.

13) вь]|пе' чем

остальнь1х

катионов.

1аблица

-с

|.||о,41з.''*

'|.г.\0а

при

|300о с

|,ь

1300

1400

1450

1500

1,0

1,9

5,5

4,4

2,5

0,4

1,2

2,4

3,2

0,5

1,5

3,5

Р:1

Ре'}

€а2*

52-

0,21

0,83

,06

!,74

2,70

4,15

4,24

5,22

(

заключению

неприменимости

уравнения

(токса

си-

ли1(атам

при1пел Р.

Аоремус

[130],

изучав1|]ий

диффузию

кис_

лорода

из пузь1рьков

расплавленнь]е

стекла. ||ри

подста_

новке значений

вя3кости и его

даннь|х

для

|о в

формулу

€токса получаются

непомерно

маль1е

радиусь1

(10_::-

\0_|2 см)

диффунлирующей

частиць|.

А.

Ф. Борисов и

Ё.

Аертев

[140]

определяли

коэффи-

циент диффузии

5!Ф2 по и3менению

во времени электродви-

)кущей

силь1

концентрационного

элемента'

одного

из элек'

тродов которого

растворялась

расплаве

}'{а2Ф

5|Фэ

плас-

тинка

51Фэ. Фни

обнару>кили'

что величина

|т1|[

не постоян-

на и

убь:вает

ростом 1,

1. €.

пони)кением температурьт.

||ереходя

другим

методам

исследования

диффузии,

от-

метим

два

способа, позволяющие

исключить

иска)кающее

вл\4ян|1е конвекции. !,ань

9и-юнь. 3. А. [ригорян

и А. А.

)[{у-

ховицкий

[141]

применили метод

вращающегося

диска'

по3-

воляющий

регулировать

конвекцию,

и сочетали его с

исполь-

3ова1{ием

меченых

атомов.

?аким способом

они

и3учали само-

диффу3ию

}келеза

в твердом

(2')

металлическом

Ре

рас-

плавленном

(|р.)

:плаке'

содер}кашем

25,78$

€аФ,

24?о 51Фа,

16?о

А1яФз'

25,4о|о

€аР2,

1,010/о

Ре,'.',7,24о10 РеФ и

1,47о Ре:Фз.

|1олуненнь:е

3}{ачения

|у"

уц

приведены

в табл.

14.

||ри

этом

величинь|

!г'

\,7

|0_э

ехр

{29000/&1}

не-

сильно

отличались

от

найденных

ранее [138]

лля

!цлаков ино-

го

состава.

7|а

215

п. м.

111урьтгин

и соавторь|

так)ке

методом

вращаю]цегося

диска

исследовали

кинетийу

растворения

твер-дь|х

}19Ф

А1яФз

в >кидких

метасиликатах

натрия \|

л|1т!4я

&19Ф

рас-

,'-'"ё

саФ-А1э@3-'5|Ф2.

Бь:численные

ими

3начения

к9?ф-

фициентов Аиффузии

со1тавляют

|*"'+

2,6'

10-6

!-1-э51Фз

й о'ьу.

10_6 в

ша]з;о,

при

1430'с,_

так}ке

1,1

'10^_5

для

-.о

А12о3-5!бэ

пЁи :6оо'с

2д:3+: 0,39

10_6

см2

сек_|

в [!э51Фз

при 1350'€'

\а6лица

ко'фф|циэптч

диффу3и|

жЁлэ'|

пРи

р!зннх

та}п|Р.туР|[

1320

1370

1420

1,1

оо

работе

Б.

А. |ригоряна'

!,а'нь

9и-юня

А.

)(уховиц_

кого

[141]

для

устранения

конвекционнь1х

помех

исполь3ова_

лась

экстраполяция

пото,ка

вещества

нулевому

диа.метру

растворяющегося

образца.

14сследовалось

взаимодействие

х<елезной

проволоки

различного

диаметра

окислами.

)келе3а

11]лаке'

,содер)кащей

8,3у'

гео,

5,1'/,

Ре2Ф3,

22,5о|о

€аФ,

49,5оь 5;оэ

!з,5%

А1:Фз.

бпреАеленнь!е

этим

методом

коэф_

фишйентьт

.}р6

Ё8

порядок

величиньт

больтпе

(0п.

1,19'

.\0_5

см2.сек_|

при

|420'

€)

привелен11ых

вь1ше,

энергия

активации очень

велика

(Ё

:76

ккал|е-атом).

|(ак отмечают

авторь1'

определеннь|е

ими

величиньт

2ве

не являются

коэффициентамй лиффузии

какого-либо

иона'

а характеризуют_обмен

местами

к6тйонов

Ре3+

и Ре2+.

Р1сходя

из

этого и

приравнивая

потоки

двухвалентного

(31р.э+1

.трехвалентного

(21р93+)

)келеза,

они

получают

сл€дующуР

.'"з"

ме*ду

*оэ6фйшиентами

лиффузии

ионов Ре2+

Ре3'|

величиной |уы.

|_:

|е

,"."*.

2""'*

[""'+

Р"',*

*""".*

'0"".*

связи

этим

необходимо

подчеркнуть'

что

тех

слу-

чаях'

когда

не

1]споль3уются

меченые

атомь|,

диффузии

участвует

как

правило'

не один'

а несколько

виАо8

ионов.

1ак

кйк

коэффйшиен'г в3аимной

диффузии

(,)

двух

сортов

частиц

уа

свя3ан

с коэффишиентами

(|'

и !д)

для

от-

дельнь1х

веществ

соотно1шением

[142]

Р'.

00,

0,.

Б),

то

для

определения

величиньт

(|д),

относящейся

к одному

компоценту

ну>кно,

чтобьт его

концентрация

бьтла

доста_

точно

мала.

1огда .[д(&в

|= |д'

1{роме

того'

если

раствор разбавлен

достаточно,

то коэф_

фицие:*т

активности

}а

п!актит{ески

не

3ависит

от состава.

согласии

вь|рах(ением

|,,-|*'(,*#3)

величина !д

в этом

случае булет

равна

коэффи:диенту

са'!1о-

лиффузии

да}-|ного

вида

настиц

(2]

,(ругими

сйовами,

определяя

в этих

условиях

каким-либо

методом

коэффициент

.Р,

мьт

получим

з'нанение

,Р,

|!ри

лиффузии

нескольких

сортов ионов'

например'

катио_

на

и аниона .4-

возни,кает

электрический потенциал

тор_

мозящий

двих(ение

ионов

одного 3нака и

ускоряющий

тако-

вое

частиц

другого

3нака. Б связи

этим

скорость

(о.;)

перемещен11я

иона | запитшется

0|:-,,(+

+,'+\.

3десь ,'

1подв;иж['Ф'€]Б,

р'

хим'ический

потенциал'

21-ч||сло

3арядов иона,

-постоянная

Фарадея' а

х-ко-

ордината

дви}<ения.

}мно>кая

!на

концентрацию

€;

@'экв|см3)'получим

потокионов

1;9е!ез

\смэ

(|4:

с1о,;). [\о-

лагая прибли>кенно,

что

р': р0+

1п

с; и

учить1вая,

что

о,:$,

находим'

что

|1риравнивая

ем,

ёр/4.х. 3атем

ходим'

что

!;:

|;$

+',',','$.

потоки

катионов

!ц

и анио|1ов [д,

исключа_

подставляем

его

вьтра}кение

для

[ц

на-

!к:

о+

216

где

|кадцдсц* 9д2кшкск

...

(ш1,25)

2кшцсц

2АцАсА

том случае'

когда

концентрация

диффундирующего

ка-

тиона' например

[62*,

он€ттБ мала по сравнению

таковой

|\ля

ан|7она'

например Ф2-, слагаемьтми € 4;с 1!1Ф)кЁо

прене-

брень. 1огда

измеряемая

величина | буд.'

равна

коэффи-

циенту

лиффузии

катиона' т. е.

2дс.

Аналогичнь:й вьтвод

бь:л сделан

еще в 1899

г. при анали3е

ьл'\яния

одного электролита

(полох<им,

(€1)

на

лиффузию

другого

(нс1)'

имеющего

ним

общий ион

[143].

|1ри

пяти-

кратном избь:тке

!(€1 электрическое

поле'

возникающее

бла_

годаря

отставанию ионов

(1_,

практически вь1равнивается ка-

тионами

калия. ||оэтому

ионьт водорода перемещаются

со

скоро,стью',определяюшейся

их

собственнь:м

коэффи:{иентом

лиффузии.

14зло>кенное

по3воляет

определять коэффициентьт само-

диффузии

ионов в

1плаке' когда их

концентрация мала' мето-

!'ам14'

не

использующими

мечень|х

атомов.

Б частности,

ю. |[. Ёикитин

[144],

применив

метод

поля_

р143аци|1

электрода

(главньтм

образом, Ре-€)

переменнь|м

током

с частотой

Ф,

оценил значения Рт"'+ в 1плаках по вели-

чине

так назь1ваемого

сопротивления

(&9)

диффузии,

рав-

ного:

&-:

э2Р2

значен,я о-

'!1

с!

1абдица

',"'+

шлак.х при

'550-|580'с

(аФ'

!о

5,о,'

^1"о",

'А

РеФ'

!о

о.|оо'

с112.сек

50, 9

37,2

30,

31,0

9,8

41,2

14,5

19,8

1,1

0,8

0,5

2,4

0,!

6,8

!(ак

следует

из табл. 15, полуненньте этим

способом

ре-

3ультать]

близкп

[1{{]

к найденньтм

другими

методами.

||рав-

да.

малое

3начение

&в,

наблюдав1шееся в этих опь|тах'

сних{а-

ет

точность

приведеннь1х

коэффишиентов

|у2-|.

217

в. и. }1усихин

[145],

измерив

предельньте

токи

(|")

кон_

центрационной

поляри3ации

при катодном

осах(дении

ряда

элементов, сделал

попь1тку сравнить

величишь|' пропорцио-

нальнь1е их коэффициентам

лиффузии

1|]лаках.

.[,опуская,

что

данном

электроли3ере

при.

фиксированной

температуре

составе

расплава

3наче!1ия

|, могут

бьтть

представлень|

формулой

[146]

.!,:2-ь.Р"|',

он

рассчитал

по экспериментально

найденнь:м !"

(ма|см2)

величинь1

Ё|.

0казалось,

что

для

<<алюминатного>>

|плака

450|о

(а0,46,7о|о

А1зФз,

6?о .]!1вФ ут

2,\о|о БэФз) значения

Ё|

при 1550"€

катионов

Ре2*, .]!1пэ+,

(о2+

и ]т{12_Р близки к

3000

!песть-семь

ра3

больтше,

чем

ион0в

в&}, т|4+, 514+, у5+,

\б{+ и

7т4+,

для

которьтх

н,о= 460'

||роме>куточное поло>ке-

ние

3анимают

ионь1

хрома и

фосфора.

3начение

Ё|

для

(т

(1600)

блих<е к таковому

для

ионов

первой группьт'

для

(800)

ко

второй.

Аналогичнь1е

ре3ультать:

бьтли

получень1

для

<<силикат-

ного>> 1плака

(40о19

€аФ,40?о

51Фэ и

20%

А12о3)

при 1460"с.

связи с такими

ра3личиями

в коэффициентах

лиффузии

бьтло

вьтсказано предполо)кение,

что ионь1

Ре, }1п,

€о,

€г

дви)кутся

виде отдельнь1х катионов'

ионь1

5!,

т|,

Б, \б и

7г

перемещаются совместно с анионом

кислорода.

Бозмо>кно,

что в последнем

случае

реали3уется

схема'

предло)кенная

для

крупнь1х

частиц

€'

[лестоном и

соавторами

[145].

|1ри этом

относительно больтпие

по

ра3меру

сочетания

ионов второй

группь]

кислородом' }1апример 5!

Ф и т.

п.' ли1пь занима-

ют места'

освободивш:иеся вследствие

перемещения

катионов

первой группь1 по

дуге

вокруг аниона Ф2_.

1ак

как

величина

такого

перемещения

велика по сравнению со

сдвигом

на ва-

кантное место' то

значения

Ё|т

3аметно

мень1пе,

чем

&!:т.

!{тобьт

сравнить энергетические

барьерьт

обеих

групп

ионов' к тем

}|(е 1плакам бьтл применен метод

осциллографии

при

заданной плотностп

тока

[1{5].

Фн

по3воляет найти

коэф-

фициент

диффузии

иона

по времени

[, прп котором

концен-

трация

|1она

становится

катода

равной

нулю'

если то:<

вь1ше

предельного

о:

4!!

л22г2с2

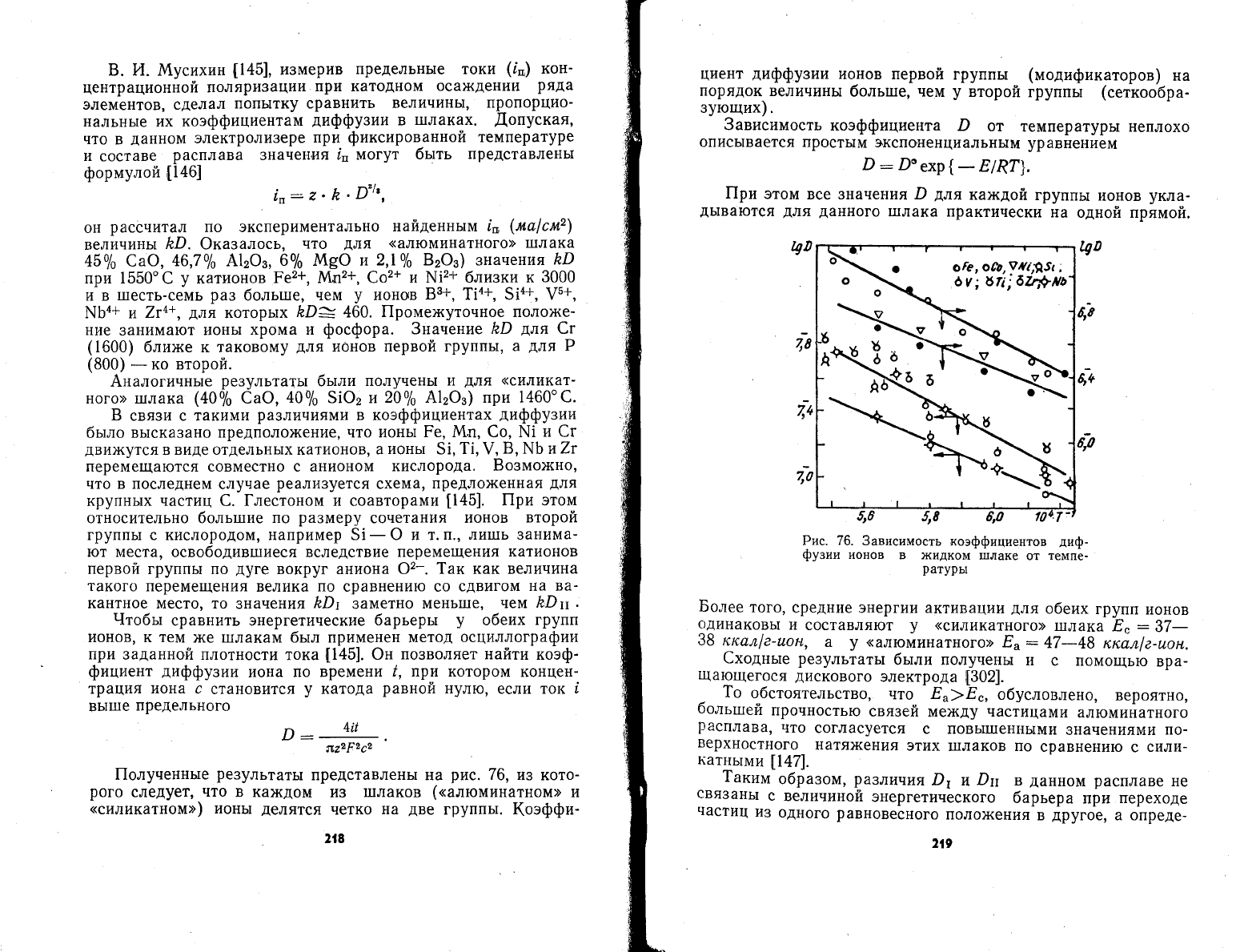
||олуненные

ре3ультать1

представлень| на

рис.

76,

из кото-

рого

следует'

что

ках(дом

из

шлаков

(<<алюминатном)>

<<силикатном>) ионьт

делятся

четко

на

две

группь[.

(оэффи-

циент лиффузии

и0нов первой

группьт

(модификаторов)

на

порядок величиньт

больп:е, чем

второй

группь|

(сеткоо6ра_

зующих).

3ависимость

коэффишиента

от

температурьт неплохо

опись|вается прость1м

3кспо'ненциальным

уравнением

Р:|"ехр{_

в/Рт\.

||ри

этом

все значения |

для

ка>кдой

группы

ионов

укла_

дь1ваются

для данного

|шлака практически

на

одной прямой.

ц'

оге'ос',1и|я5.;

ёт

;

6т!;

67'#шо

ч0

Рис. 76. 3ависимость

коэффициентов

лиф_

фузии

ионов

Ё#{ьт

1цлаке

от темпе_

Более

того'

средние энергии акт14ъац|1и

для

обеих

групп

ионов

одинаковь1

составляют

<<силикатного>>

1плака

Ё"

37-

ккал|

е-шон,

<<алюминатного>>

Ба:47-48

ккал|

е-шон'

€ходнь:е

результать1

бьтли получе1ь1

с помощью

вра-

щающегося

дискового

электрода

[302].

?о

обстоятельство'

что

Б'}Ё",

обусловлено,

вероятно'

больтшей

прочностью

связей мех{ду частицами

алюминатного

расплава'

что

согласуется

с повь11пеннь1ми

значениями

по-

верхностного

натя)кения

этих

1плаков по

сравнению

сили-

катньтшти

[147].

1аким

образом,

различия

|т

Ртх

данном

расплаве

не

свя3ань|

величиной

энергетического

барьера

при

переходе

частиц

и3

одного

равновесного

поло}кения

другое'

а опреде_

7,0

7,4

7'|

т.

5'8