Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

2.1.

Релейная

обратная

связь

При выполнении условия |/| < 1 исследование стабилизируемости

системы (2.13) сводится к анализу устойчивости нуля уравнений

Х2 = -Sgn(x2 + CXi).

(2.14)

Для исследования этой системы построим ее фазовый портрет, кото-

рый получается в результате "сшивания" по линии о- = жг + cxj = О

фазовых траекторий двух систем

_ Г 3Ci = Х2, г -• /

XI - Х2,

XI - -1,

действующих, соответственно, в полуплоскостях (т <

и (т > 0.

2.1.9. Скользящий реж:им на отрезке

Траектории систем Ei,S2 — суть параболы, которые при с > О рас-

положены так, как это показано на рис. 2.24. На рисунках обозна-

£7 = 0

Рис.

2.24

(т=0

чены две точки Aw. В, являющиеся точками касания фазовых траек-

торий систем Ej и Ег прямой линии

= 0. Координаты этих точек

определяются из условий касания (о- = О, (Т = 0): А = (1/с^,—1/с),

В — (—l/c"^, 1/с). После "сшивания" фазовых траекторий получаем

итоговый фазовый портрет, изображенный на рис. 2.25.

V Vi*

Рис.2

.25

С^

сг=0

Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

Из рис. 2.25 можно сделать выводы о том, что:

• отношение 1/L < 1 и, следовательно, изображающая точка за ко-

нечное число переключений релейного элемента попадает на отре-

зок АВ;

• на отрезке АВ идет "встречное" движение по фазовым траекто-

риям систем El и Ег и, следовательно, изображающая точка не

может покинуть отрезок АВ, т.е. возникает скользящий режим.

Для нахождения уравнения движения в скользящем режиме прове-

дем эвристические рассуждения. В режиме скольжения

(7 = Х2 + СХ1 = О,

но по определению

Х\ = ж, Х2 = Xi

Значит, за уравнение скольжения можно принять уравнение вида

+ сх = 0.

При О

оно экспоненциально устойчиво, что влечет за собой устой-

чивость рассматриваемой релейной системы.

2.1.10. Реальный скользящий режим на отрезке

Пусть в релейной системе (2.14) имеется пространственное запаздыва-

ние Д в переключении релейного элемента, т.е. фактически мы имеем

дело с системой

_ f ii = ^2

Ч^й.

{X2

+ CXi).

(2.15)

Для получения ее фазового портрета следует наложить фазовые

портреты систем Ef (рис. 2.2ба) и Ej ( 2.2б<5). Тогда в результате мы

* . "*\i » '

^ .i\

Х2

Рис.

2.26

2.1.

Релейная

обратнгл

связь

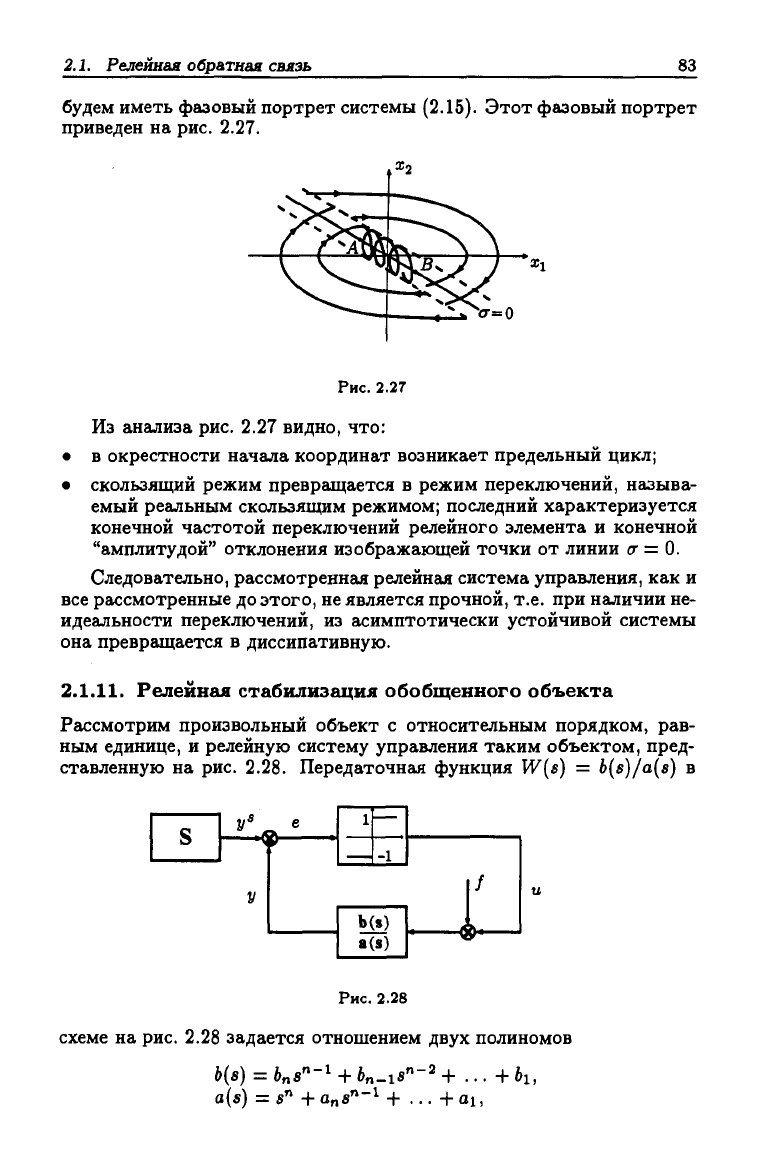
будем иметь фазовый портрет системы (2.15). Этот фазовый портрет

приведен на рис. 2.27.

.Х2

v=o

Рис.

2.27

Из анализа рис. 2.27 видно, что:

• в окрестности начала координат возникает предельный цикл;

• скользящий режим превращается в режим переключений, называ-

емый реальным скользящим режимом; последний характеризуется

конечной частотой переключений релейного элемента и конечной

"амплитудой" отклонения изображающей точки от линии

(Г

= 0.

Следовательно, рассмотренная релейная система управления, как и

все рассмотренные до этого, не является прочной, т.е. при наличии не-

идеальности переключений, из асимптотически устойчивой системы

она превращается в диссипативную.

2.1.11.

Релейная стабилизация обобщенного объекта

Рг1ссмотрим произвольный объект с относительным порядком, рав-

ным единице, и релейную систему управления таким объектом, пред-

ставленную на рис. 2.28. Передаточная функция W{s) = h{s)/a{s) в

—

-1

b(s)

a(s)

' Ч

у'

Рис.

2.28

схеме на рис. 2.28 задается отношением двух полиномов

6(s)=6„e"-l+6„_iS"-2-l-...-b6i,

a(s) = в"-Н a„s"-^ + ... +01,

84 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

откуда следует, что устойчивость системы в нуле при условии |/| < 1

возможна только тогда, когда полином b{s) гурвицев, а полином a(s)

не имеет нулей в правой полуплоскости переменной s и не более двух

его нулей лежит на мнимой оси плоскости переменной s. Подобные

объекты называют минимально фазовыми.

Из сказанного выше следует вывод о том, что релейная обратная

связь является стабилизирующей, если:

• объект минимально фааовый;

• имеет относительный порядок г < 2;

• задание и возмущение равномерно ограничены.

Кроме того, релейные системы не являются прочными, а их решения,

а значит, и их свойства зависят от возмущений.

2.2.

Стабилизация объекта

с неопределенным оператором

Качественно новую ситуацию в объекте управления создает неопре-

деленность, в частности,' неопределенность параметрическая. Для ре-

шения задачи стабилизации необходимо привлечение новых методов

синтеза и алгоритмов управления. Рассмотрению некоторых уже из-

вестных подходов к этой проблеме и посвящен настоящий раздел.

2.2.1.

Общие положения

При расчете обратной связи обычно используется математическая мо-

дель объекта с оператором Р (рис. 2.29а), однако, как правило, опе-

ратор объекта управления известен с некоторой погрешностью АР, и

поэтому фактически стабилизируется объект с неопределенным опе-

ратором Р + АР (рис. 2.296). Если погрешность ДР в определен-

/ /

Р+ДР

Рис.

2.29

ном смысле мала, а регулятор R, рассчитанный по точной модели

Р,

делает замкнутую систему (рис. 2.30а) прочной, то тот же са-

мый регулятор годится и для стабилизации неопределенного объекта

(рис.

2.306). Математическим выражением прочности замкнутой си-

стемы управления служит сохранение качественного поведения дина-

мической системы при вариации условий задачи, в частности, при

малых регулярных и сингулярных возмущениях.

2.2.

Стабилизация объекта

с неопределенным

оператором

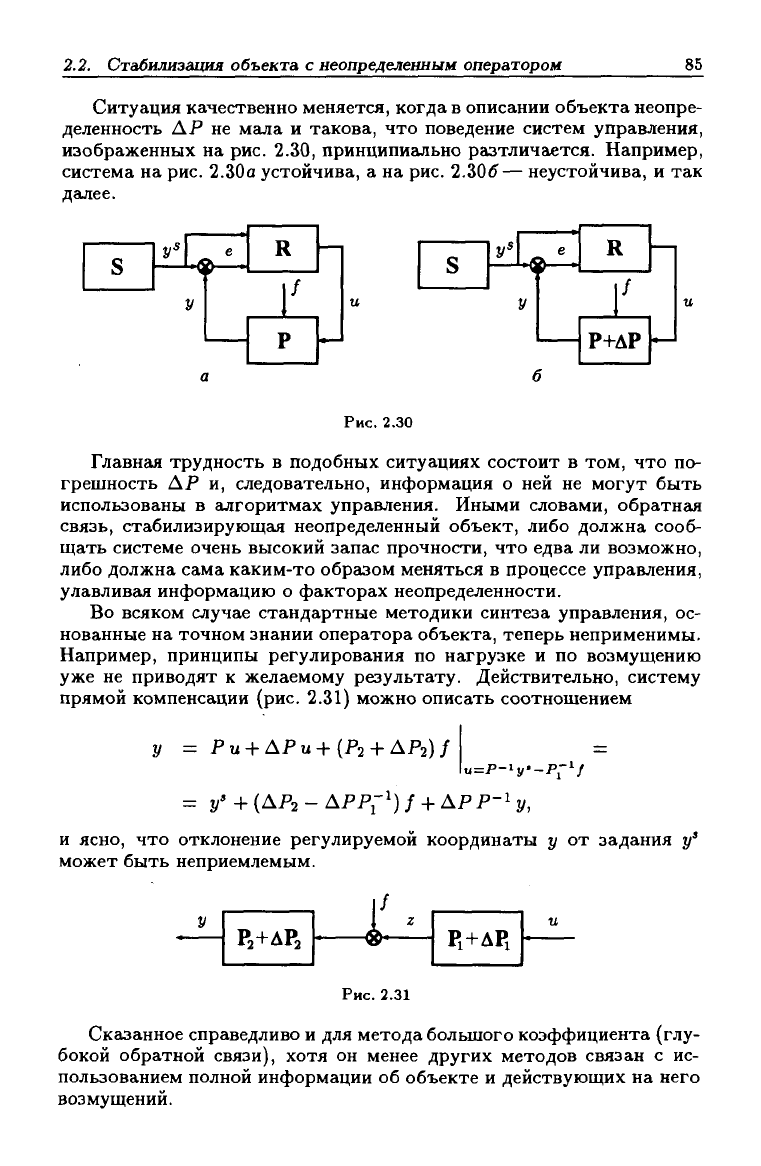
Ситуация качественно меняется, когда в описании объекта неопре-

деленность АР не мала и такова, что поведение систем управления,

изображенных на рис. 2.30, принципиально разтличается. Например,

система на рис. 2.30а устойчива, а на рис. 2.306— неустойчива, и так

далее.

у'

е R

!/*

Р+АР

Рис. 2.30

Главнгш трудность в подобных ситуациях состоит в том, что по-

грешность АР и, следовательно, информация о ней не могут быть

использованы в алгоритмах управления. Иными словами, обратная

связь, стабилизирующая неопределенный объект, либо должна сооб-

щать системе очень высокий запас прочности, что едва ли возможно,

либо должна сама каким-то образом меняться в процессе управления,

улавливая информацию о факторах неопределенности.

Во всяком случае стандартные методики синтеза управления, ос-

нованные на точном знании оператора объекта, теперь неприменимы.

Например, принципы регулирования по нагрузке и по возмущению

уже не приводят к желаемому результату. Действительно, систему

прямой компенсации (рис. 2.31) можно описать соотношением

у = Pu + APu+(P2 + AP2)f

u=P-'-y-P-^f

у'

+ (ДРг - АРР^^) f + AP Р-1 у,

и ясно, что отклонение регулируемой координаты у от задания у'

может быть неприемлемым.

P,+AR

Pi+APi

Рис. 2.31

Сказанное справедливо и для метода большого коэффициента (глу-

бокой обратной связи), хотя он менее других методов связан с ис-

пользованием полной информации об объекте и действующих на него

возмущений.

86 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

В самом деле, рассмотрим последствия, которые возникают при

устремлении коэффициента к к бесконечности (рис. 2.32), где струк-

'" 6

Р+ЛР

Рис. 2.32

тура воздействия возмущения /(<) та же, что и в системе на рис. 2.31.

Уравнение этой системы управления имеет вид

y = {P + AP)kRe + {P2 + ДРг) /•

Поскольку е = у'

—

у, то для ошибки стабилизации имеем выражение

е = —к {Р + АР) Re — (Рг + АРг) /. После приведения подобных и

деления на к получаем уравнение

+ {P + AP)R

e = ~(P2 +

AP2)f.

В пределе, при к -> ос, возникает уравнение {Р + AP)R = е, ко-

торое ответственно за основные черты поведения системы с Ьлубо-

кой обратной связью. Видно, что это поведение зависит от факторов

неопределенности. Следовательно, глубокая обратная связь в общем

случае не обеспечивает стабилизацию неопределенного объекта.

Если, однако, неопределенность каким-либо способом структури-

рована, то возможности по стг1билизации такого неопределенного объ-

екта расширяются. Пусть, например, неопределенность в операторе

объекта АР может быть приведена к управляющему входу. В этом

случае говорят, что неопределенность удовлетворяет условию согласо-

ванности или, иначе, matching condition (МС-условию). При выполне-

нии МС-условия неопределенный объект можно представить схемой,

изображенной на рис. 2.33. Для такого объекта применение глубо-

АР

-Л-

Рис. 2.33

2.2.

Стабилизация объекта

неопределенным

оператором

кой обратной связи может дать желательный результат,

т.е.

застг^би-

лизировать неопределенный объект

при

устремлении коэффициента

обратной связи

к к

бесконечности

по

схеме

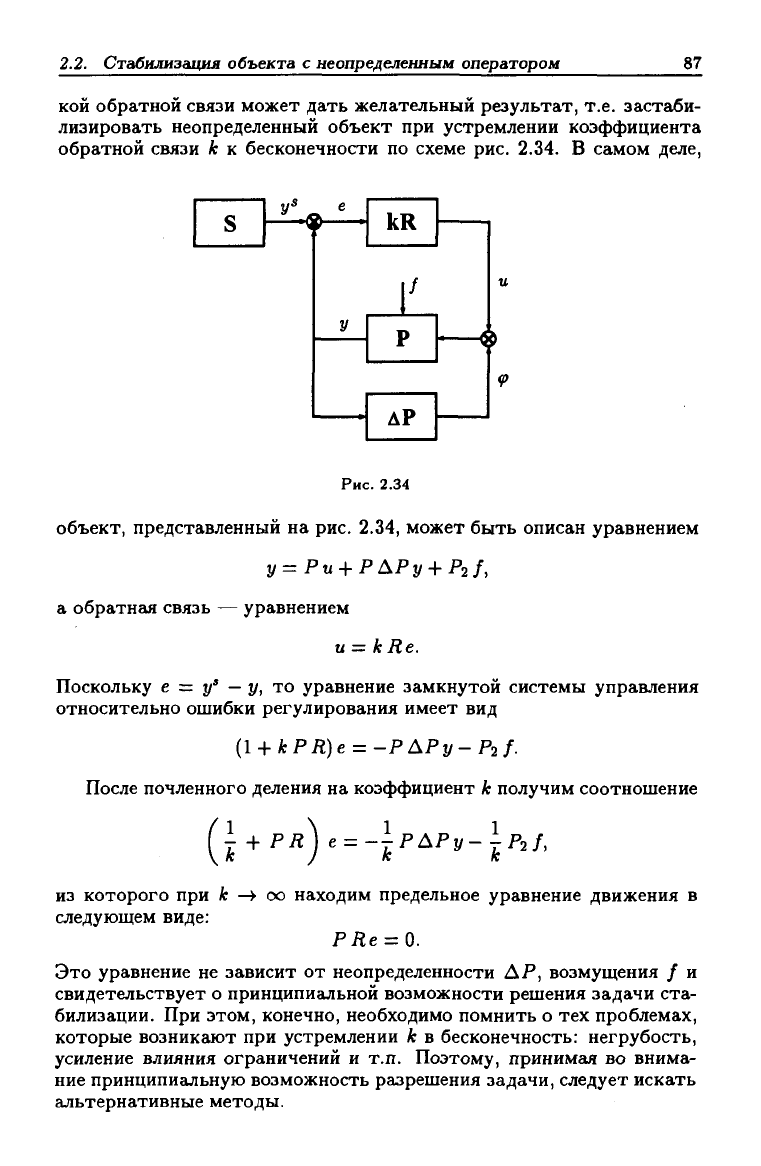
рис. 2.34. В

самом деле.

)

АР

•

|ф|

Рис.

2.34

объект, представленный

на рис. 2.34,

может быть описан уравнением

= Pu +

PAPy

+ P2f,

а обратная связь

—

уравнением

= к Re.

Поскольку

е = J/'

—

у, то

уравнение замкнутой системы управления

относительно ошибки регулирования имеет

вид

kPR)e

= -PAPy-P2f.

После почленного деления

на

коэффициент

получим соотношение

+ PR)e = -lpAPy-lp2f,

из которого

при fc

—>

находим предельное уравнение движения

следующем виде:

PRe

Это уравнение

не

зависит

от

неопределенности

АР,

возмущения

/ и

свидетельствует

принципиальной возможности решения задачи ста-

билизации.

При

этом, конечно, необходимо помнить

о тех

проблемах,

которые возникают

при

устремлении

к в

бесконечность: негрубость,

усиление влияния ограничений

и т.п.

Поэтому, принимая

во

внима-

ние принципиальную возможность разрешения задачи, следует искать

альтернативные методы.

Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

2.2.2.

Принцип каскадного регулирования

Как выяснилось, весьма часто простым увеличением коэффициента

усиления главной обратной связи (рис.2.34) задача стабилизации не

решается, так как предельная система неустойчива. Напомним, что

для устойчивости при введении глубокой обратной связи по выходу

необходимо, чтобы объект был минимально фазовым и имел относи-

тельный порядок г < 2.

Понятно, что эти условия выполняются далеко не всегда. По-

этому представляют интерес методы, использующие местные глубо-

кие обратные связи, когда указанные выше условия реализуются ло-

кально, в каком-то месте структурной схемы системы.

Такие местные глубокие обратные связи, надлежащим образом со-

гласованные, порождают иерархию коэффициентов усиления и связан-

ную с этим раэнотемповость движений в различных контурах обрат-

ных связей. Одновременно это часто упрощает синтез управления,

так как при решении локальной задачи стабилизации обычно имеют

дело с системой более низкого порядка по отношению к порядку ис-

ходной системы.

Часто разнотемповость в системе имеет физическую природу (на-

пример, в электромеханических системах), и поэтому подобный спо-

соб управления не кажется искусственным. Такую иерархию глубоких

обратных связей вводит принцип каскадного регулирования.

Пример 11. Иерархия обратных связей. Рассмотрим задачу ста-

билизации в нуле объекта, покгъзанного на рис. 2.35. Считается, что кон-

i + Xj

^— ттг '—^—

S + A.1

Рис.

2.35

станты Ai, Лг и внешние силы /i, /2 неизвестны, а для управления могут

использоваться только координаты у и г.

Дифференциальные ургшнения этого объекта имеют вид

Аг

у = /г

-Н

г,

Xi Z

= fi + и.

(2.16)

(2.17)

Очевидно, что в этой задаче условия применимости стандартных методов

компенсации не выполнены. Определенные трудности возникают и 1фи ис-

пользовании обычной глубокой обратной связи, так как возмущение /г не

удовлетворяет МС-условию. Поэтому организация обрей'ной связи по име-

ющейся информации

u = -k{cy+z) (2.18)

2.2.

Стабилизация объекта с неопределенным оператором

и устремление к -^ оо не дает требуемого результата, так как предельная

система описывается ургщнением

y + {c + \-i)y = /2,

(2.19)

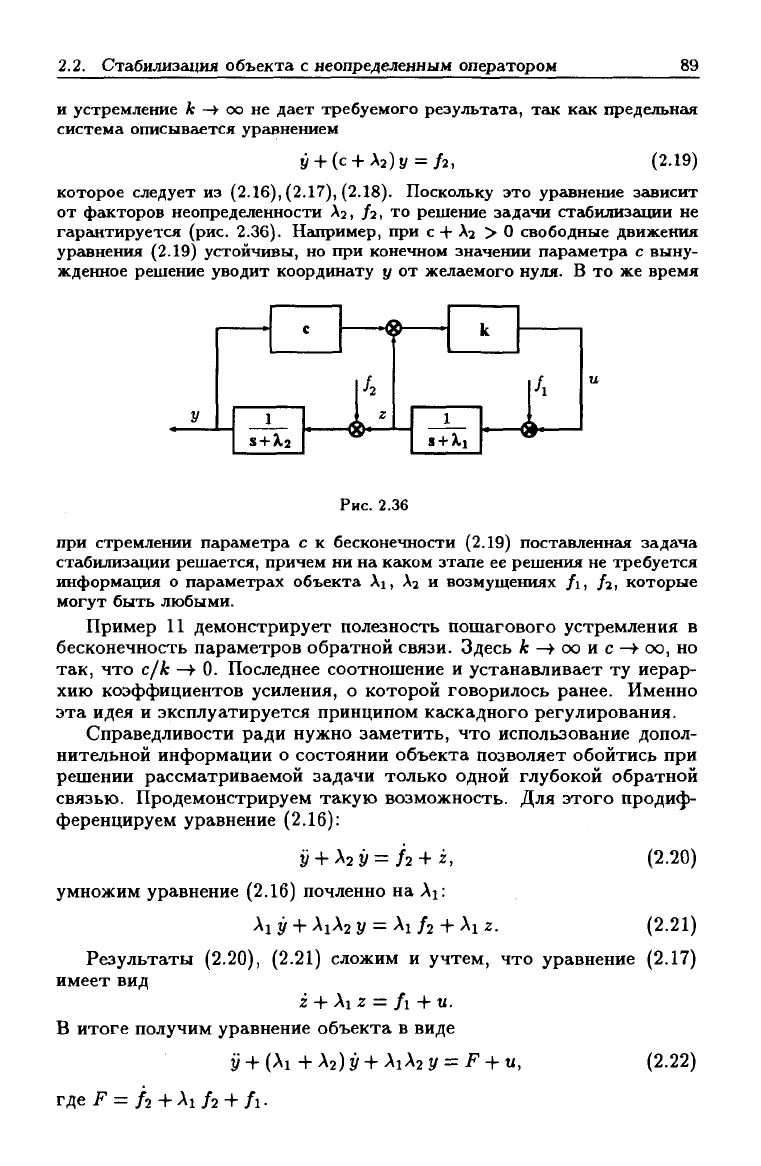
которое следует из (2.16), (2.17), (2.18). Поскольку это ургквнение згшисит

от фсккторов неопределенности Аг, /г, то решение задачи стабилизгщии не

гарантируется (рис. 2.36). Например, при с + Лг > О свободные движения

уравнения (2.19) устойчивы, но при конечном значении параметра с выну-

жденное решение уводит координату у от желаемого нуля. В то же время

S+Xi

Рис.

2.36

при стремлении параметра с к бесконечности (2.19) поставленная задача

стабилизации решается, причем ни на каком этапе ее решения не требуется

информация о параметрах объекта Ai, А2 и возмущениях /i, /2, которые

могут быть любыми.

Пример 11 демонстрирует полезность пошагового устремления в

бесконечность параметров обратной связи. Здесь Л

—)•

оо и с

—»•

ос, но

так, что с/к

—)•

0. Последнее соотношение и устанавливает ту иерар-

хию коэффициентов усиления, о которой говорилось ранее. Именно

эта идея и эксплуатируется принципом каскадного регулирования.

Справедливости ради нужно заметить, что использование допол-

нительной информации о состоянии объекта позволяет обойтись при

решении рассматриваемой задачи только одной глубокой обратной

связью. Продемонстрируем такую возможность. Для этого продиф-

ференцируем уравнение (2.16):

+ Лгу = /2 +г, (2.20)

умножим уравнение (2.16) почленно на Ai:

AiJ/ + AiA2y = Ai/2 + Aiz. (2.21)

Результаты (2.20), (2.21) сложим и учтем, что уравнение (2.17)

имеет вид

Z + Xi Z = fi + и.

В итоге получим уравнение объекта в виде

i/ + (Ai+A2)y + AiA2y=:F-i-ti, (2.22)

где F = /2 + Ai/2 + /i-

Глава 2. Некоторые принципы построения нелинейных регуляторов

Достоинство полученного уравнения (2.22) состоит в том, что те-

перь возмущение согласовано с управлением, т.е. удовлетворяет МС-

условию, поэтому использованная процедура и называется приведе-

нием возмущения к управляющему входу. При этом, конечно, нужно

допустить дифференцируемость функции /гСО-

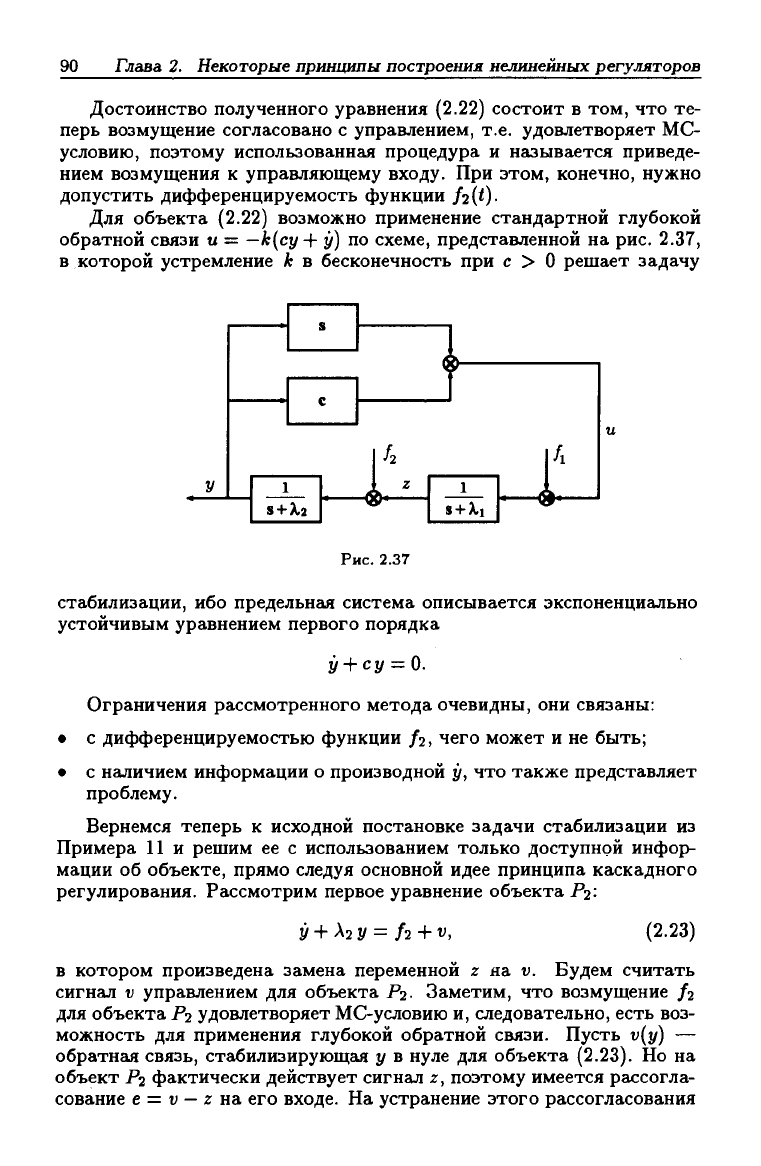
Для объекта (2.22) возможно применение стандартной глубокой

обратной связи и = —к{су + у) по схеме, представленной на рис. 2.37,

в которой устремление к в бесконечность при с > О решает задачу

s + Xi

^ s + Xi ^

Рис.

2.37

стабилизации, ибо предельная система описывается экспоненциально

устойчивым уравнением первого порядка

у + су = 0.

Ограничения рассмотренного метода очевидны, они связаны:

• с дифференцируемостью функции /г, чего может и не быть;

• с наличием информации о производной у, что также представляет

проблему.

Вернемся теперь к исходной постановке задачи стабилизации из

Примера 11 и решим ее с использованием только доступной инфор-

мации об объекте, прямо следуя основной идее принципа каскадного

регулирования. Рассмотрим первое уравнение объекта Рг:

У+

>^2У

f2-\-V,

(2.23)

в котором произведена замена переменной z на v. Будем считать

сигнал V управлением для объекта Рг- Заметим, что возмущение /г

для объекта Рг удовлетворяет МС-условию и, следовательно, есть воз-

можность для применения глубокой обратной связи. Пусть v(y) —

обратнгш связь, стгьбилизирующая у в нуле для объекта (2.23). Но на

объект Рг фактически действует сигнал z, поэтому имеется рассогла-

сование е =

V —

Z на. его входе. На устранение этого рассогласования