Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

2.3.

Стабилизация

регулятором переменной

структуры

111

характеристического полинома замкнутой системы

a(s)S'(s)s'"+^-\-k'y{s)

(2.46)

требуется выполнение неравенства deg f{8) > m + 1. Если полином

(2.46) гурвицев, то система слежения без ошибки воспроизводит по-

линомиальный сигнал (2.45), и тогда говорят, что регулятор

R{8)

fis)

'+1

S'{s)

(2.47)

обеспечивает астатизм (m + 1)-го порядка. Заметим, что, в силу из-

вестного разложения экспоненты

»а«

{atr

г!

т=0

задачу слежения за экспоненциально растущим сигналом

y'{t)

= y4oy

можно интерпретировать как задачу построения системы с бесконеч-

ным порядком астатизма.

Ясно,

что указанным выше способом построить такую систему

слежения нельзя из-за неограниченно возрастающей сложности регу-

лятора. Это наблюдение только подтверждает сделанный ранее вывод

о том, что

• в рамках линейной теории невозможно построение робастной аста-

тической следящей системы.

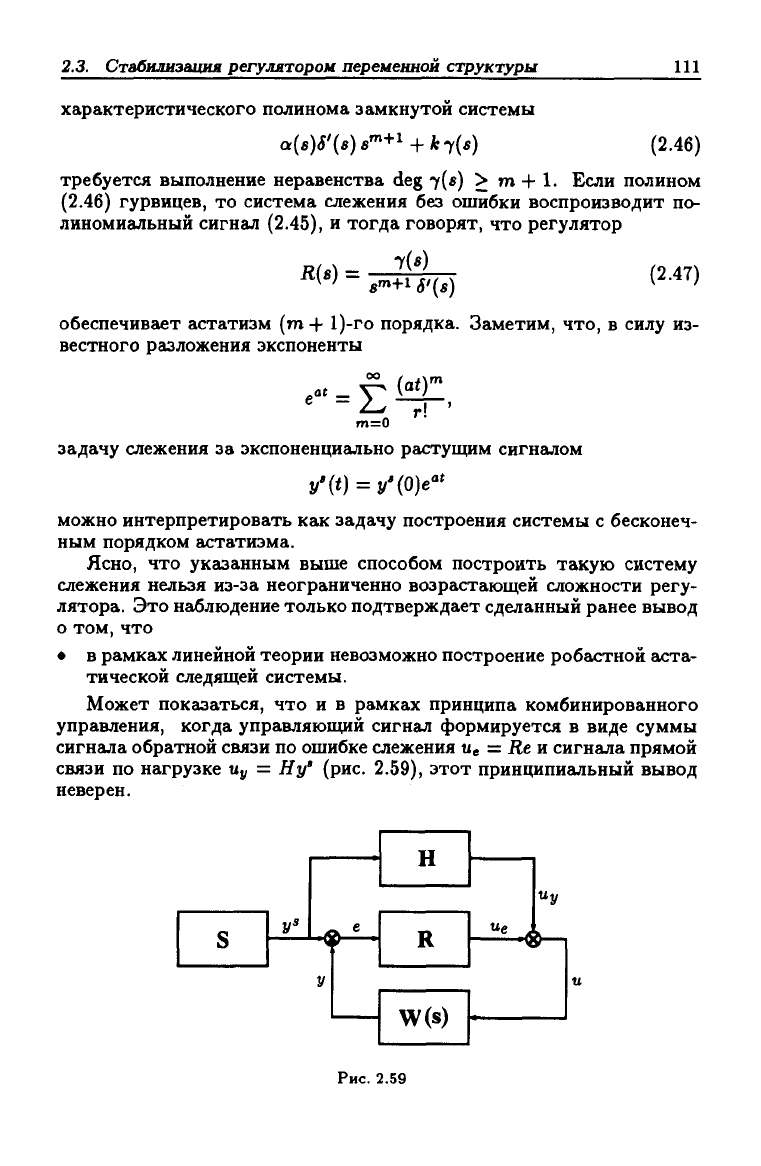
Может показаться, что и в рамках принципа комбинированного

управления, когда управляющий сигнал формируется в виде суммы

сигнала обратной связи по ошибке слежения и^ = Ле и сигнала прямой

связи по нагрузке Uy = Ну' (рис. 2.59), этот принципиальный вывод

неверен.

У^

^ «

Рис. '

W(s)

2.59

"Ч

>—1

112 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

Разберем и эту ситуацию, полагая, как и ранее, что W{s) ~ l/a(s),

R[s) = j{s)/5{s). Из рис. 2.59 имеем следующее уравнение движения

относительно ошибки:

a{s) е

—

a{s) у'

—

= [a{8)-H{s)]y'-R{s)e.

u=Hy'+Re

После приведения подобных имеем дело с уравнением

[ais)S{s)+y{s)]e = S{s)[a(s) - H{s)]y'. (2.48)

В (2.48) оператор прямой связи H{s) надлежит выбрать так, чтобы

правая часть обратилась в тождественный нуль. Имеется несколько

очевидных возможностей решения этой задачи.

Способ I. Можно, например, положить

H{s) = a{s),

тогда прямая связь определяется выражением

«у = a(s) у'

и предполагает п-кратное точное дифференцирование задающего сиг-

нала (напомним, что deg a(s) = п). По неоднократно приводившимся

выше соображениям от этого решения, как неробастного, приходится

отказываться.

Способ П. Можно понизить кратность дифференцироваЦия вос-

производимого сигнала

y'(t),

если

deg /C(s) < deg a{s),

где K.{s) — оператор, аннулирующий

y'[t).

В самом деле, поделим по-

лином a{s) на IC(s), так как, вообще говоря, все нули tC{s) не являются

нулями

oi{s).

В результате деления получится некий остаток y{s), т.е.

a{s) = a'{s)ICis) + T,is), (2.49)

причем справедливы неравенства

deg y{s) < deg

K-{s)

< deg a{s).

Теперь для достижения г1статизма достаточно (при том условии, что

характеристический полином (p(s) = a(s) J(s) + j(s) — гурвицев) по-

ложить

H(s) = ф). (2.50)

Подставляя (2.50) в (2.49), а результат — в (2.48), получаем уравнение

[а{8) Sis) + f(s) ] е = 5(8) [e'(s)

IC{s)

+ ф) - n{s) ]у'=0,

из которого и следует сказанное выше.

2.3.

Стабилизация регулятором переменной структуры

113

Способ III. Если же

deg K.{s) > deg a{s)

и у оператора K{s) есть устойчивые нули, т.е. он представим в виде

IC{s) = lC-{s)K+{s),

где /C_(s) — гурвицев полином, то эти нули можно включить в число

нулей полинома S(s), т.е. взять последний в виде

S(s)^S'(s)IC-{s).

Если при этом еще окажется, что

deg lC+{s) <deg a(s),

то возможен синтез оператора прямой связи H{s) по той же схеме, что

и в Способе II. При невыполнении последнего неравенства использо-

вание прямой связи по нагрузке кардинальным образом не влияет на

возможность построения астатической следящей системы.

Из приведенного выше анализа следует, что в любом случае потре-

буется операция точного многократного дифференцирования, что не

позволяет говорить о решении рассматриваемой задачи.

Пример 14. Точное слежение за задающим воздействием. Про-

иллюстрируем теоретические выкладки предыдущего раздела на простей-

шем примере и рассмотрим следующую постановку задачи: требуется син-

тезировать обратную связь, обеспечивающую точное слежение регулируе-

мой координатой у за задающим воздействием у' (рис. 2.60). Уравнение

•V

Рис.

2.60

системы слежения относительно ошибки е таково: ё = у'

то задачу решает любг1я обратная связь вида

и = ке, к = const > О,

и. Если у' = О,

так как в этом случае уравнение замкнутой системы ё — —ке экспонен-

щ1ально устойчиво. Если же у' ^ О, нашример у' = const (т.е. задание

растет линейно), то статическая обратная связь и = ке уже не решает за-

дачу, так как уравнение движения в отклонениях имеет ненулевую правую

114 Глава 2.

Некоторые

прииципы

построения

нелинейных регуляторов

часть

в положении равновесия ё =

—ке

+ у', и, следовательно, появляется

статииеская ошибка, т.е. установившееся при t

—>

оо значение ошибки регу-

лирования е(оо) = у'/к. Разумеется, увеличением коэффициента усиления

обратной связи к эту погрешность слежения можно устранить, но при этом

возникают характерные для систем с глубокой обратной связью проблемы,

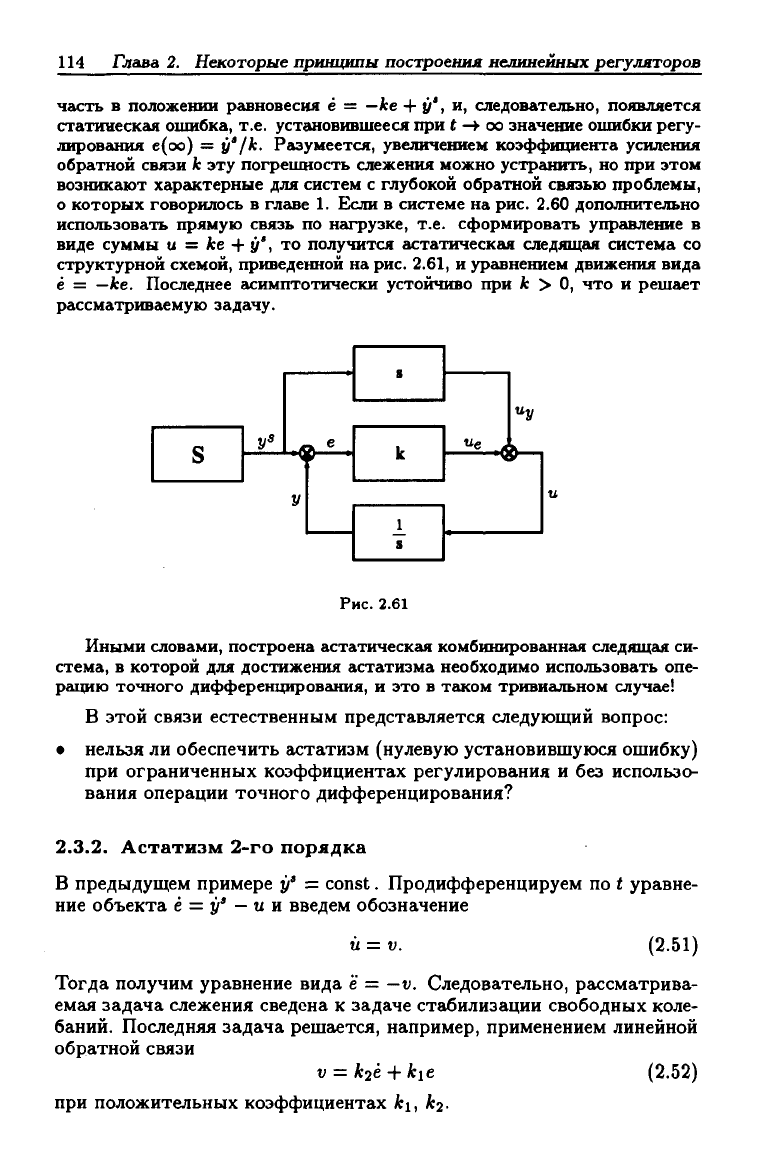
о которых говорилось в главе 1. Если в системе на рис. 2.60 дополнительно

использовать прямую связь по нагрузке, т.е. сформировать управление в

виде суммы

= ке + у', то получится астатическая следящая система со

структурной схемой, приведенной на

рис.

2.61, и уравнением движения вида

ё = —ite. Последнее асимптотически устойчиво при

А;

> О, что и решает

рассматриваемую задачу.

"«<L

Рис.

2.61

Иными словами, построена астатическгш комбинированнгья следящая си-

стема, в которой для достижения астатизма необходимо использовать опе-

рацию точного дифференцирования, и это в таком тривиальном случг^е!

В этой связи естественным представляется следующий вопрос:

• нельзя ли обеспечить астатизм (нулевую установившуюся ошибку)

при ограниченных коэффициентах регулирования и без использо-

вания операции точного дифференцирования?

2.3.2.

Астатизм 2-го порядка

В предыдущем примере у' = const. Продифференцируем по t уравне-

ние объекта ё = у'

—

и и введем обозначение

и = V.

(2.51)

Тогда получим уравнение вида ё = —v. Следовательно, рассматрива-

емая задача слежения сведена к задаче стг^билизации свободных коле-

баний. Последняя задача решается, например, применением линейной

обратной связи

v = k2e + kie (2.52)

при положительных коэффициентах ki, к^-

2.3.

Стабилизация

регулятором переменной

структуры

115

Действительно, соответствующая замкнутая система управления

описывается устойчивым уравнением ё + Лгё + kie = 0. Из (2.51)

и (2.52) получг^м искомую обратную связь в виде пропорционально-

S ^

1—

к, —1

Рис.

2.62

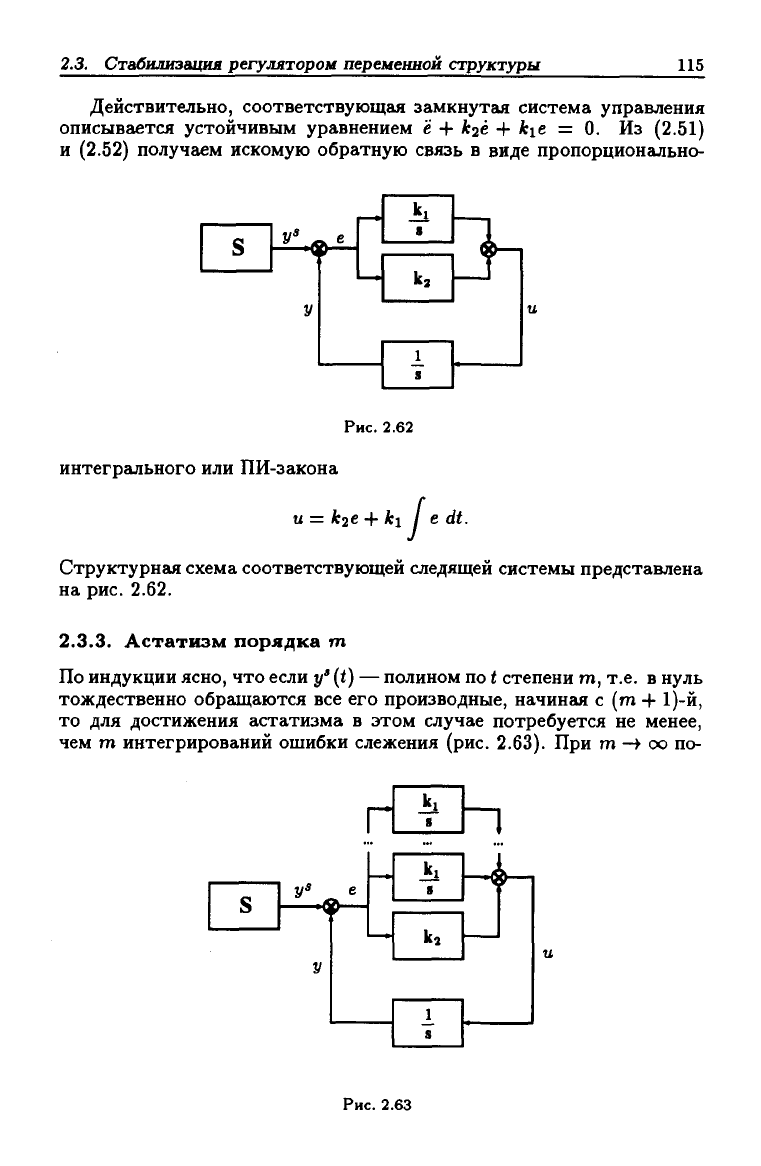
интегрального или ПИ-закона

и = Лгс + ki I е dt.

Структурная схема соответствующей следящей системы представлена

на рис. 2.62.

2.3.3.

Астатизм порядка т

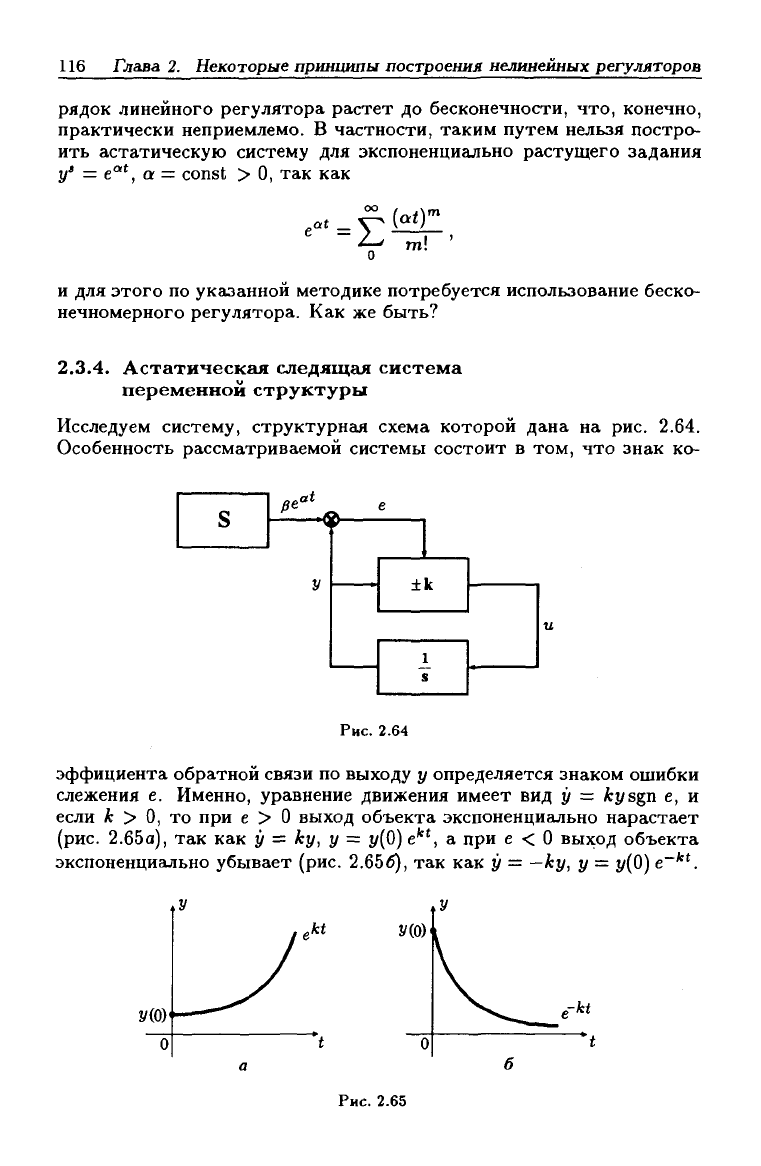
По индукции ясно, что если у' (t) — полином по t степени т, т.е. в нуль

тождественно обращаются все его производные, начиная с (т + 1)-й,

то для достижения астатизма в этом случае потребуется не менее,

чем m интегрирований ошибки слежения (рис. 2.63). При m

—>

оо по-

У-

кг

^ ,

Рис.

2.63

116 Глава 2. Некоторые принципы построения нелинейных регуляторов

рядок линейного регулятора растет до бесконечности, что, конечно,

практически неприемлемо. В частности, таким путем нельзя постро-

ить астатическую систему для экспоненциально растущего задания

у'

= е"', а = const > О, так как

иг

т!

и для этого по указанной методике потребуется использование беско-

нечномерного регулятора. Как же быть?

2.3.4. Астатическая следящгкя система

переменной структуры

Исследуем систему, структурная схема которой дана на рис. 2.64.

Особенность рассматриваемой системы состоит в том, что знак ко-

,e^'^

Рис.

±к

2.64

эффициента обратной связи по выходу у определяется знаком ошибки

слежения е. Именно, уравнение движения имеет вид у = ку sgn е, и

если ^ > О, то при е >

выход объекта экспоненцигшьно нарастает

(рис.

2.65а), так как у

ку, у = у(0)е*', а при е <

выход объекта

экспоненциально убывает (рис. 2.656), так как у = —ку, у = у(0) е~**.

У(0)'

.у

Рис.

2.65

2.3.

Стабилизация регулятором переменной структуры

117

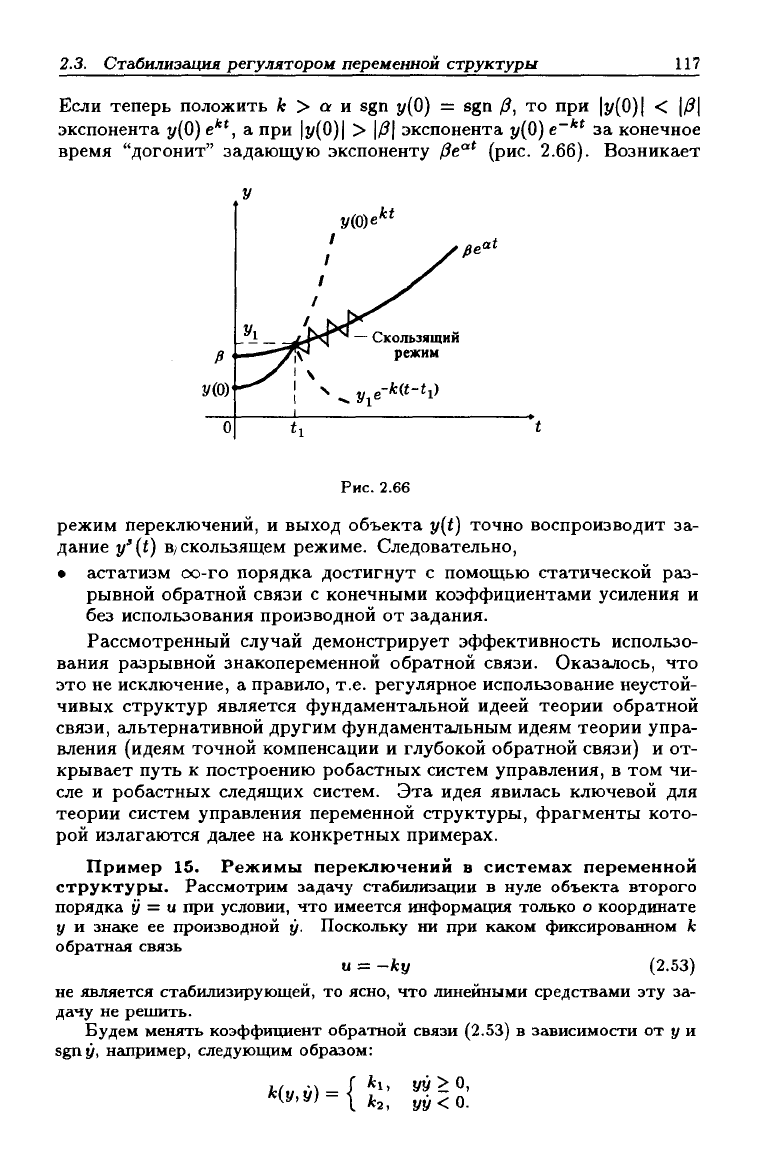
Если теперь положить к > а и sgn j/(0) = sgn /?, то при |j/(0)| < (/?|

экспонента j/(0) е**, а при |j/(0)| > |/?| экспонента у(0) е~*' за конечное

время "догонит" задающую экспоненту

/Зе"*^

(рис. 2.66). Возникает

У(0)

_^J_

у(0)е'='

1 ^/^

-^Jr^C^

—

Скользящий

Tlv^ режим

1 ^ ^ y^e-^^W-*!)

Рис.

2.66

режим переключений, и выход объекта y[t) точно воспроизводит за-

дание y'{t)

скользящем режиме. Следовательно,

• астатиэм оо-го порядка достигнут с помощью статической раз-

рывной обратной связи с конечными коэффициентами усиления и

без использования производной от задания.

Рассмотренный случай демонстрирует эффективность использо-

вания разрывной знакопеременной обратной связи. Оказалось, что

это не исключение, а правило, т.е. регулярное использование неустой-

чивых структур является фундаментальной идеей теории обратной

связи, альтернативной другим фундаментгшьным идеям теории упра-

вления (идеям точной компенсации и глубокой обратной связи) и от-

крывает путь к построению робастных систем управления, в том чи-

сле и робастных следящих систем. Эта идея явилась ключевой для

теории систем управления переменной структуры, фрагменты кото-

рой излагаются далее на конкретных примерах.

Пример 15. Режимы переключений в системах переменной

структуры. Рассмотрим задачу стабилизации в нуле объекта второго

порядка у = и при условии, что имеется информация только о координате

у и знаке ее производной у. Поскольку ни при кгжом фиксированном к

обратная связь

= -ку (2.53)

не является стабилизирующей, то ясно, что линейными средствами эту за-

дачу не решить.

Будем менять коэффициент обратной связи (2.53) в зависимости от у и

sgn у, например, следующим образом:

к(у,у) =

{

ки

*2,

УУ>0,

УУ<0.

118 Глава 2. Некоторые принципы построения нелинейных регуляторов

Тогда замкнутая система упргшления имеет разрывную обратную связь

и описывгкется уравнением

у = -к{у,у)у.

(2.54)

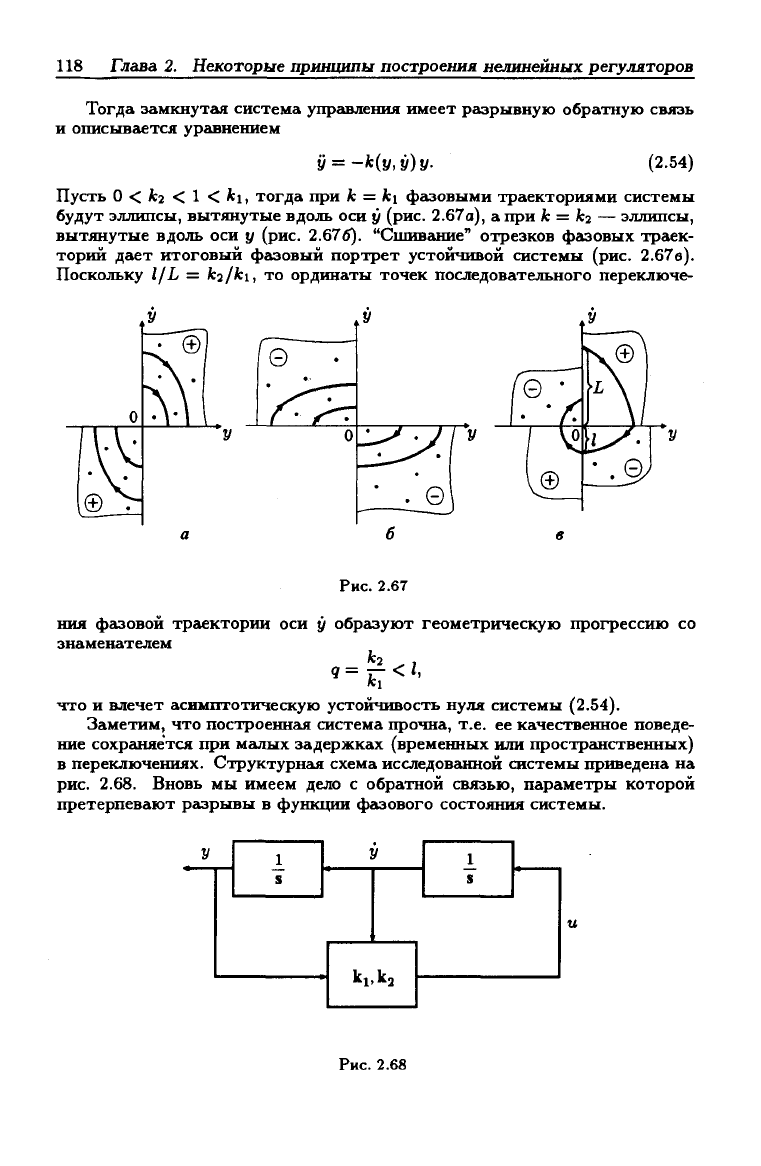
Пусть О < к2 < 1 < ki, тогда при к = ki фазовыми траекториями системы

будут эллипсы, вытянутые вдоль оси у (рис. 2.67а), а при к = к2 — эллипсы,

вытянутые вдоль оси у (рис. 2.676). "Сшивание" отрезков фазовых трг1ек-

торий дг1ет итоговый фг13овый портрет устойчивой системы (рис. 2.67в).

Поскольку 1/L = /cj/fci, то ординаты точек последовательного переключе-

^•?г

К®)

•

• .^

Рис.

2.67

ния фазовой траектории оси у образуют геометрическую прогрессию со

знаменателем

ki ,

что и влечет асимптотическую устойчивость нуля системы (2.54).

Заметим, что построенная система прочна, т.е. ее качественное поведе-

ние сохраняется при малых задержках (временных или пространственных)

в переключениях. Структурнгш схема исследованной системы приведена на

рис.

2.68. Вновь мы имеем дело с обратной связью, параметры которой

претерпевают разрывы в функции фазового состояния системы.

kl.kj

Рис. 2.68

2.3.

Стабилизация регулятором переменной структуры 119

Пример 1в. Системы переменной структуры с движением по

вырожденным траекториям. Рассмотрим задачу стабилизации в нуле

объекта

у=и

при условии, что в обратной связи может быть использована информация

о регулируемой координате у и знаке линейной комбинации

(Г = у + су, с = const > 0. (2.55)

Вновь ясно, что никакгш линейнгья обратная связь вида

= -ку

не решсъет задачи стабилизации. Сделгъем коэффициент к разрывным, на-

пример, по следующему пргшилу:

/ \ / с^. ус^ > О,

тогда получим систему с разрывной обратной связью, описываемую ургш-

нением

У= -c^|y|sgn а.

Для анализа этой системы используем метод фазовой плоскости. В

области ytr > О (на рисунке она обозначена знаком ф) поведение системы

описывается уравнением у = —с'у, его фазовые траектории — эллипсы

(рис.

2.69а). При у<т < О (на рисунке эта область обозначена знаком G)

движение подчинено уравнению у = с*у и его фазовые траектории — ги-

перболы (рис. 2.696). В результате "сшивания" фазовых траекторий по гра-

ницам разрыва получгьем асимптотически устойчивую систему (рис. 2.69в).

В исследуемой системе стсъбилизации каждая тргъектория за конечное время

сг=0

Рис.

2.69

достигает линии

<г

и далее не покидает ее. Действительно, в силу (2.55)

выполнено равенство

-1-

су =

и y(t)

—> О

при t

—>

О, что и требовалось.

120 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

Недостаток данной системы управления состоит в ее непрочности.

Малые задержки в переключениях качественно меняют ее поведение:

апериодические переходные процессы могут стать колебательными

(рис.

2.70а) или даже может наступить неустойчивость (рис. 2.706).

s^^ \

;

Рис. 2.70

2.3.5. Скользящий режим на всей прямой

При рассмотрении режимов переключения и движения по вырожден-

ным траекториям выявляются определенные достоинства принципа

переменности структуры, в том числе: простота закона обратной

связи, уменьшение объема информации, необходимой для стабилиза-

ции объекта по сравнению с линейной обратной связью. Но видны

и недостатки этих режимов: колебательность переходного процесса

в режиме переключений и трудность организации движения по выро-

жденным траекториям при изменении параметров объекта и действии

внешних сил. Не имеют в этих случаях простого ответа и вопросы,

связанные с прочностью систем управления, а также с возможностью

переноса методов синтеза на многомерные системы. Поэтому актуа-

лен следующий вопрос:

• возможно ли при сохранении достоинств принципа переменности

структуры устранение или ослабление указанных выше недостат-

ков?

Ответ на этот вопрос положителен, но для этого следует использовать

скользящий режим на прямой.

Пример 17. Скользящий режим на прямой. Вновь рассмотрим

задачу стабилизации в нуле объекта

у = и

при условии, что в обратной связи возможно использование информации

о координате у и знаке линейной комбинации <т = у -)- су, с = const > 0.

Ясно,

что линейнс1я обратная связь и = —ку ни при каком фиксированном

коэффшдаенте к задачу не решает.