Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

2.4. Библиографический

комментарий

131

окрестности (т = О, негативно сказываются на работе механиче-

ских и электромеханических приводов, которые весьма часто ис-

пользуют на практике в качестве силовых установок. Это обсто-

ятельство делает невозможным практическое использование клас-

сических СПС.

• Моделирование стандартного скользящего режима на дискретной

ЭВМ возможно только методами 1-го порядка (Эйлера, Адамса и

т.д.),

так как методы более высоких порядков требуют существо-

вания производных от правой части дифференциального уравне-

ния. Это условие не выполняется для уравнений, описывающих

СПС.

При "дискретном" скольжении имеют место следующие со-

отношения:

(T~0(/i),

6-~0(/i),

где Л — шаг дискретизации, которые означают, 'что отклонение

траекторий от линии скольжения пропорционально шагу дискре-

тизации. Для повышения точности скольжения нужно уменьшать

шаг дискретизации h, что немедленно приводит к увеличению вре-

мени расчетов, так как последние имеют порядок 1/h. Именно это

обстоятельно делает невозможным прямое использование СПС по

скользящим режимам в системах прямого цифрового управления,

• Трудности стабилизации неопределенного объекта с относитель-

ным порядком г, таким, что 1<г<п

—

1. В значительной степени

эти трудности связаны с получением информации о состоянии не-

определенной системы, в частности, с получением "хороших" оце-

нок производных выходного сигнала объекта.

В связи с перечисленными обстоятельствами можно сформулировать

следующую проблему: построить систему управления со свойствами

идеальной СПС, но с гладкой обратной связью, прочной по отно-

шению к регулярным, сингулярным, функциональным и структурным

возмущениям. Эта проблема и рги;сматривг1ется во второй части мо-

нографии.

2.4.

Библиографический комментарий

Интерес к исследованию разрывных систем возник очень давно, на-

пример, в классической механике он появился в связи с анализом влия-

ния кулоновского трения и гистерезисных явлений, а в электротехнике

и радиотехнике — в связи с появлением стг1билизаторов, различных

генераторов, экономичных усилителей мощности и т.п.

Было замечно, что релейные системы склонны к автоколебаниям,

но наряду с этим некоторые движения в релейных системах мало чув-

ствительны к параметрам и потому оказались полезными при компен-

сации влияния факторов неопределенности на свойства системы ре-

гулирования. Потребность в целенаправленном использовании этого

132 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

свойства, а также необходимость в средствах подавления автоколеба-

ний привели к созданию теории релейных систем. На первых этапах

значительный вклад в эту теорию внесли Х.Л- Хазен (H.L. Hazen) [91],

И. Флюгге-Лотц (I. Flugge-Lotz) [90] и Я.З. Цыпкин [75]. С совре-

менным состоянием теории релейных систем можно ознакомиться по

книгам [9, 14].

Интерес современной теории управления к релейным системам свя-

зан прежде всего с задачами оптимального быстродействия при огра-

ниченных ресурсах [60, 94]. Некоторые г1спекты релейной стабилиза-

ции в условиях неопределенности рг1Ссмотрены в работе [7]. Матема-

тические методы анализа скользящих режимов, возникающих в релей-

ных системах, можно найти в [71]. Проблемам управления неопреде-

ленными объектами посвящено много работ, см., например, [46, 55,

69,

73, 74, 76]. Основы теории систем автоматического управления

переменной структуры изложены в монографии [15].

Часть II

Новые типы обратной связи

Во второй части монографии излагаются теоретические основы по-

строения нового класса нелинейных систем автоматического управле-

ния. Математическую основу построения таких систем управления

составляет принцип бинарности, в соответствии с которым коорди-

наты и операторы нелинейных управляемых систем рассматриваются

в виде единой совокупности ее переменных состояния и между ними

не проводится принципиального различия. Более того, каждый эле-

мент такой совокупности может выступать в качестве координаты

или оператора, а содержательная интерпретация переменной состоя-

ния предопределена ее ролью в конкретном локальном преобразова-

нии, и эта роль может, разумеется, меняться от преобразования к

преобразованию. Это означает, что операторы могут подвергаться

преобразованиям, аналогичным тем, которые используются для пре-

образования координат. Это обстоятельство немедленно ведет к необ-

ходимости введения новых типов обратной связи, когда целью обрат-

ной связи служит не формирование переменной, как в классической

теории регулирования, но оператора.

Сочетание принципа бинарности с принципом регулирования по

отклонению позволяет перейти к автоматическому формированию за-

конов управления в условиях, когда априорной информации недоста-

точно для прямого синтеза обратной связи, сообщающей замкнутой

системе управления требуемой совокупности свойств.

Во второй части развивается понятийный аппарат новой теории,

синтезируются обобщенные структуры замкнутых систем с новыми

типами обратной связи. Значительное внимание уделяется анализу

конкретных примеров.

Библиографическая справка. Общие принципы теории но-

вых типов обратной связи сформулированы в [18, 19, 79]. Первое

систематическое изложение этой теории можно найти в [17]. Раз-

134 Новые

типы обратной

связи

личным ее аспектам посвящены работы [20, 21, 37-42, 85-88]. Ста-

билизация неопределенных систем с использованием нестандартной

обратной связи рассмотрена в работах [26-28, 31-36, 44, 45, 81-84].

Математическая теория разрывных систем разработана А.Ф. Фи-

липповым в работе [72], а с различными прикладными аспектами

стандартных скользящих режимов можно ознакомиться в трудах [9,

14,

68]. Скользящим режимам высших порядков посвящены работы

[22,

23, 80]. Наиболее подробное на сегодня изложение этой теории

содержится в статье [25].

С проблемой получения высококачественных производных сигна-

лЬв можно ознакомиться по работам [1, б, 49]. Математические во-

просы дифференцирования рассмотрены в монографии [66], различ-

ные дискретные аппроксимации можно найти в книге [65], современ-

Н£1Я

трактовка проблемы дифференцирования дана в [2].

Проблема оптимального управления в ее современном виде офор-

милась благодаря ргьботам Л

.С.

Понтрягина (принцип максимума) [63]

и Р. Беллмана (принцип оптимальности) [4]. Оптимальное управле-

ние — наиболее прорг1ботанный и динамично развивающийся раздел

теории управления. Классическая теория представлена в рг1ботах [3,

8, 10, 50, 54, 70, 94]. Численные аспекты оптимального управления

обсуждались в монографии [59]. Современная трактовка основных

идей оптимального управления дана в книге [51]. Обобщения изло-

женного в разделе метода субоптимального управления можно найти

в работах [29, 30, 43].

Глава 3

Общие положения теории

новых типов обратной связи

Основу новой теории составляет принцип бинарности, раскрывающий

двойственную природу сигналов в нелинейных динамических систе-

мах: сигналы могут выступать либо в качестве переменных, над ко-

торыми осуществляются преобразования, либо в качестве операто-

ров,

определяющих эти преобразования. Принцип бинарности позво-

ляет возложить синтез оператора стабилизирующей обратной связи

на вспомогательную нелинейную систему с обратной связью. Разви-

тие этой концепции и соответствующих методик синтеза привело к

необходимости рассмотрения трех новых типов обратной связи: опе-

раторной, операторно-координатной и координатно-операторной.

В данной главе излагаются основные понятия, определения и прин-

ципы построения систем автоматического управления с новыми ти-

пами обратной связи.

3.1.

Вводные замечания

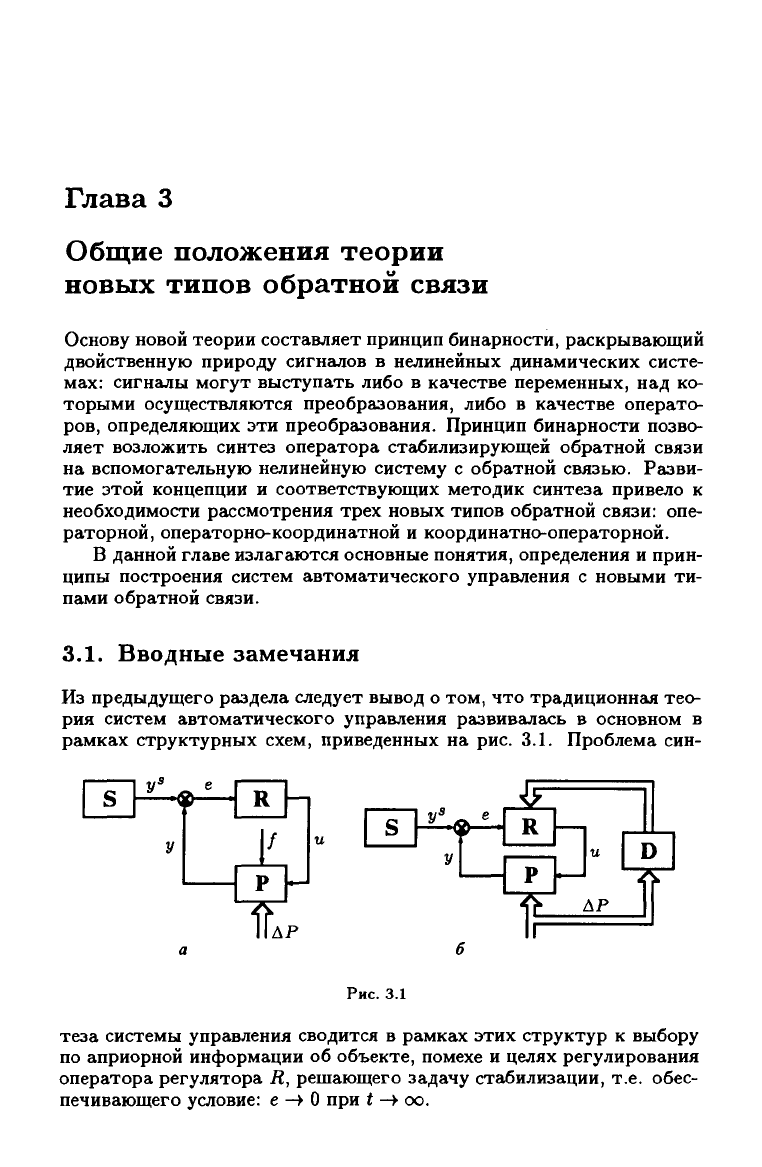
Из предыдущего раздела следует вывод о том, что традиционная тео-

рия систем автоматического управления развивалась в основном в

рамках структурных схем, приведенных на рис. 3.1. Проблема син-

%р

lle-L

АР

Рис. 3.1

теза системы управления сводится в рамках этих структур к выбору

по априорной информации об объекте, помехе и целях регулирования

оператора регулятора R, решающего задачу стс1билизации, т.е. обес-

печивающего условие: е

—»•

при t -> оо.

136 Глава 3. Теория новых

типов обратной

связи

Если априорной информации достаточно для решения задачи син-

теза, т.е. информация точна и допускаются лишь малые отклонения

АР от модели линейного оператора Р, а внешних сил / —• от их вол-

новой модели, если, кроме того, цели регулирования заданы не очень

"жестко", то для синтеза стабилизирующего оператора R вполне при-

менимы описанные в предыдущем разделе классические методы син-

теза.

В тех случаях, когда отклонение АР не мало, а об изменениях ха-

рактеристик объекта управления можно получить в режиме on-line не-

обходимую информацию, в таких случаях можно организовать, также

в режиме on-line, поднастройку оператора обратной связи R по схеме

на рис. 3.15, принятой в теории адаптивного управления.

Если же изменения оператора объекта АР происходят интенсивно

и к тому же неконтролируемым образом, помеха / не является волно-

вой, кроме того, сформулированы "строгие" требования к качеству

регулирования, а также имеются ограничения на фазовые перемен-

ные и управление, то традиционные методы синтеза стабилизиру-

ющих регуляторов неприменимы и следует искать новые подходы к

синтезу САУ в таких сложных условиях.

При определении направления поиска, как обычно, полезно обра-

титься к опыту и аналогиям. Вспомним, что принцип обратной связи

заменил принцип регулирования по возмущению, когда это возмуще-

ние стало неизвестным. И если при известном возмущении целью син-

теза регулятора было получение "программы" u'{t), то при отсут-

ствии информации о возмущении целью синтеза регулятора стало по-

лучение его оператора R, вырабатывающего требуемый сигйал упра-

вления u{t) с помощью обратной связи. Сами же значения сигнала u{t)

стали несущественными, важно лишь то, что при правильном выборе

оператора R замкнутая система управления имеет требуемое свой-

ство,

а именно

e{t) ->

О,

t ^ 00.

Указанный выше переход от формирования сигнала к формированию

оператора, вырабатывающего нужный сигнал, можно возвести в прин-

цип и дать ему, например, следующую формулировку:

• при дефиците информации следует переходить от программного

формирования функции (элемента) к синтезу алгоритма (опера-

тора),

генерирующего функцию.

Как функция времени u{t) — элемент некоторого множества допусти-

мых управлений, так и оператор R — только элемент множества И

стабилизирующих обратных связей. Поэтому для получения требуе-

мого оператора R при дефиците информации используем сформулиро-

ванный выше принцип. Именно, будем синтезировать не сам опера-

тор обратной связи R, но алгоритм его формирования, а поскольку

все это происходит в условиях неопределенности, то без механизма

обратной связи здесь не обойтись. Заметим, что эта идея является

явной альтернативой идее адаптивного управления (рис. 3.16), когда с

3.2. Система базовых понятий

137

помощью процедуры идентификации реализуется "программная" ге-

нерация требуемого оператора R.

Сформулированный выше принцип впредь будем называв принци-

пом генерации. Разумеется, принцип генерации может быть распро-

странен и на формирование алгоритма, генерирующего оператор R, и

т.д.

и т.п. При применении принципа генерации естественным обра-

зом возникают следующие первоочередные вопросы:

• каким образом осуществлять синтез контура генерации;

• что будет ошибкой или регулируемой координатой такого контура;

• что следует применять в качестве регулирующего органа в этом

контуре;

• можно ли из этой идеи извлечь практическую выгоду, ведь контур

генерации можно рассматривать как часть регулятора, и откуда

следует, что такой синтез регулятора "по частям" проще синтеза

регулятора "в целом".

На некоторые из этих вопросов ответы даются легко, на другие

однозначных ответов нет вообще. Это означает, что в реализации

намеченного плана по автоматическому синтезу стабилизирующих ре-

гуляторов в условиях неустранимой неопределенности по априорной

и текущей информации много эвристики и произвола. 0тчг1сти это

можно устранить с помощью следующей системы базовых понятий.

3.2. Система базовых понятий

Для придания развиваемой теории конструктивного характера нам

потребуется ряд нестандартных для классической теории управления

понятий, и ключевое из них вводится в следующем пункте.

3.2.1.

Сигнал-оператор

Для обозначения того, что изменению подвергается оператор, будем

применять двойную стрелку (рис. 3.2). Соответствующую перемен-

ную обозначаем буквами греческого алфавита, например //, и пазы-

Рис.

3.2

138

Глава 3. Теории новых

типов обратной

связи

BBjeu

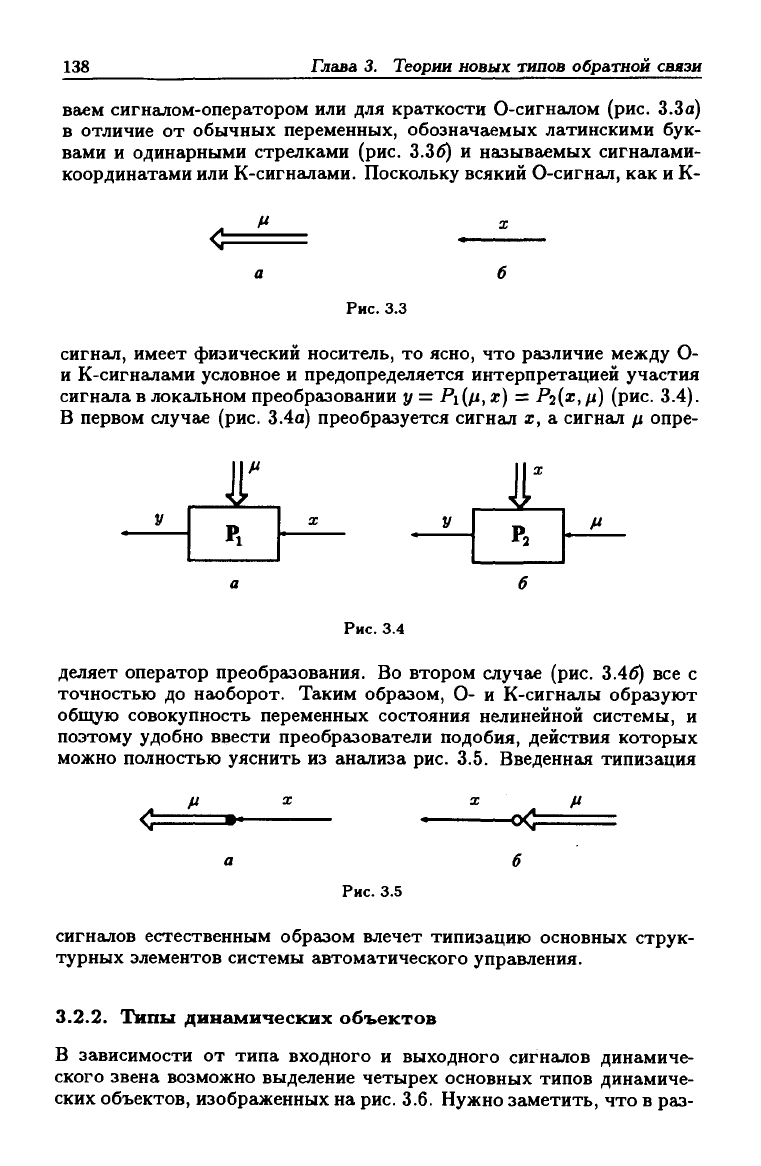
сигналом-оператором или для краткости 0-сигналом (рис. 3.3а)

в отличие от обычных переменных, обозначаемых латинскими бук-

вами и одинарными стрелками (рис. З.Зб) и называемых сигнгиами-

координатами или К-сигнг1лами. Поскольку всякий 0-сигнал, как и К-

Рис. 3.3

сигнал, имеет физический носитель, то ясно, что различие между О-

и К-сигналами условное и предопределяется интерпретацией участия

сигнала в локальном преобразовании у = Pi(n, х) = Р2{х, /i) (рис. 3.4).

В первом случае (рис. 3.4а) преобразуется сигнал х, а сигнал /i опре-

Рис. 3.4

деляет оператор преобразования. Во втором случае (рис. 3.46) все с

точностью до наоборот. Таким образом. О- и К-сигналы образуют

общую совокупность переменных состояния нелинейной системы, и

поэтому удобно ввести преобразователи подобия, действия которых

можно полностью уяснить из анализа рис. 3.5. Введенная типизация

Рис. 3.5

сигналов естественным образом влечет типизацию основных струк-

турных элементов системы автоматического управления.

3.2.2.

Типы динамических объектов

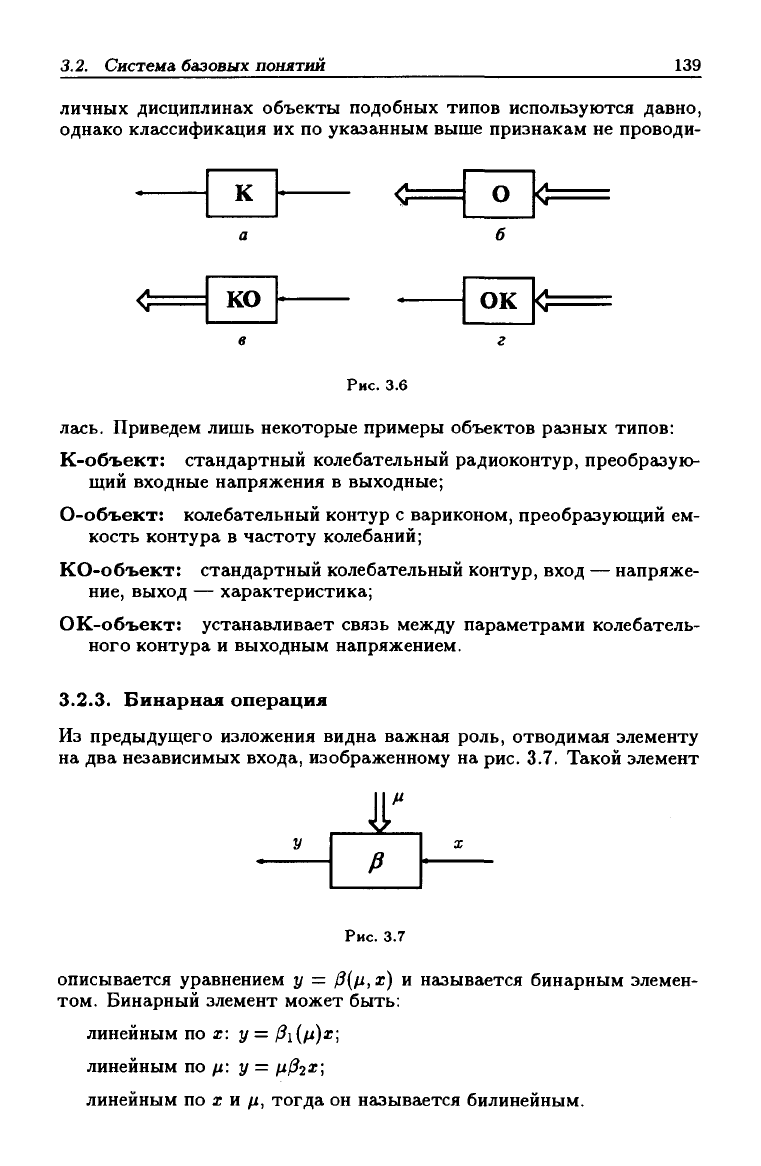
В зависимости от типа входного и выходного сигнгиюв динамиче-

ского звена возможно выделение четырех основных типов динамиче-

ских объектов, изображенных на рис. 3.6. Нужно заметить, что в раз-

3.2.

Система

базовых понятий

139

личных дисциплинах объекты подобных типов используются давно,

однако клги:сификация их по указанным выше признакам не проводи-

ко ок d

Рис.

3.6

лась.

Приведем лишь некоторые примеры объектов разных типов:

К-объект: стандартный колебательный радиоконтур, преобразую-

щий входные напряжения в выходные;

О-объект: колебательный контур с вариконом, преобразующий ем-

кость контура в частоту колебаний;

КО-объект: стандартный колебательный контур, вход — напряже-

ние,

выход — характеристика;

ОК-объект: устанавливает связь между параметрами колебатель-

ного контура и выходным напряжением.

3.2.3.

Бинарная операция

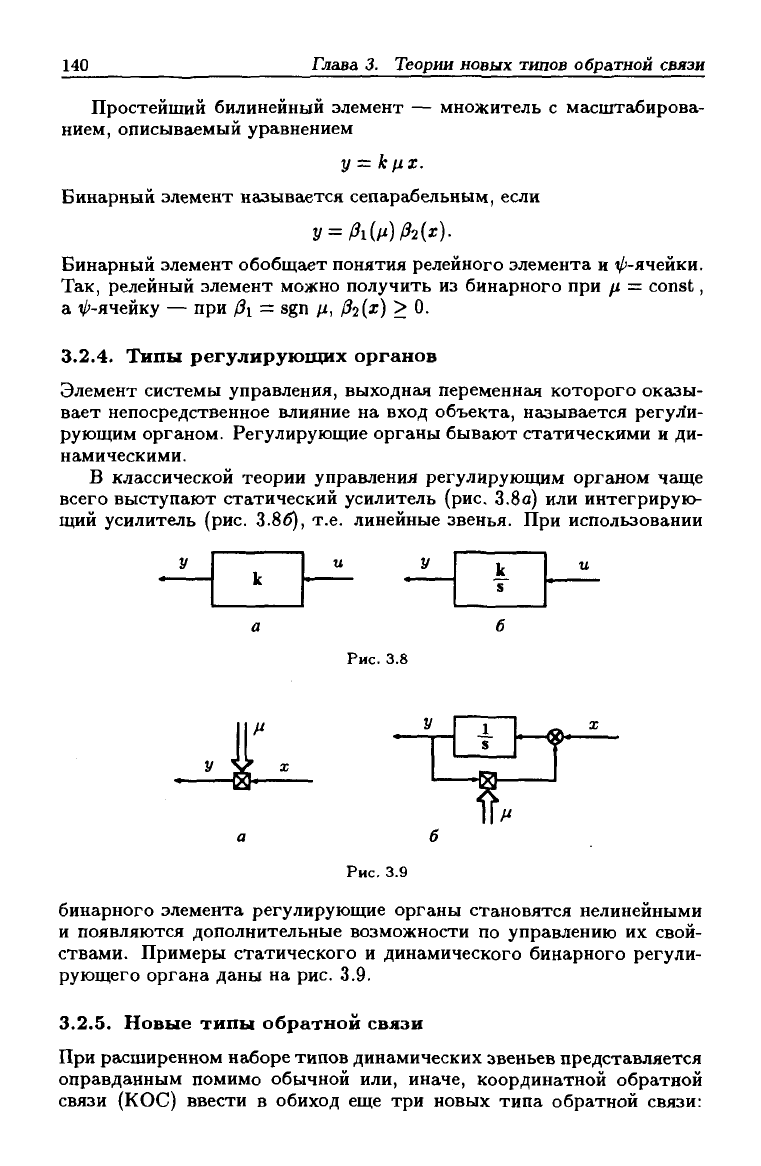
Из предыдущего изложения видна важная роль, отводимая элементу

на два независимых входа, изображенному на рис. 3.7. Такой элемент

К.

Рис. 3.7

описывается уравнением у = /?(^, х) и называется бинарным элемен-

том. Бинарный элемент может быть:

линейным по х: у = ;3i(/i)x;

линейным по /х: у = ц02х;

линейным по Z и /i, тогда он называется билинейным.

140 Глава 3. Теории новых

типов обратной

связи

Простейший билинейный элемент — множитель с масштабирова-

нием, описываемый уравнением

у ~ к fix.

Бинарный элемент называется сепарабельным, если

Бинарный элемент обобщгьет понятия релейного элемента и V'-ячейки.

Так, релейный элемент можно получить из бинарного при fi = const,

а ^/'-ячейку — при /?i = sgn fi, /32{x) > 0.

3.2.4.

Типы регулирующих органов

Элемент системы управления, выходная переменная которого оказы-

вает непосредственное влияние на вход объекта, называется регул'и-

рующим органом. Регулирующие органы бывают статическими и ди-

намическими.

В классической теории управления регулирующим органом чаще

всего выступают статический усилитель (рис. 3.8а) или интегрирую-

щий усилитель (рис. 3.86), т.е. линейные звенья. При использовании

Рис. 3.8

«h.

Рис. 3.9

бинарного элемента регулирующие органы становятся нелинейными

и появляются дополнительные возможности по управлению их свой-

ствами. Примеры статического и динамического бинарного регули-

рующего органа даны на рис. 3.9.

3.2.5. Новые типы обратной связи

При расширенном наборе типов динамических звеньев представляется

оправданным помимо обычной или, иначе, координатной обратной

связи (КОС) ввести в обиход еще три новых типа обратной связи: