Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

3.3.

Структурный

синтез бинарных

систем

151

нимизирующего "расстояние" между jf и у, т.е.

-Popt = argminr(j/* - у),

где г(-,) — надлежащим образом определенное расстояние, напри-

мер,

среднеквадратическое уклонение, когда речь идет о случайных

сигналах.

Стандартно сигналы х и ^ считаются случайными процессами с

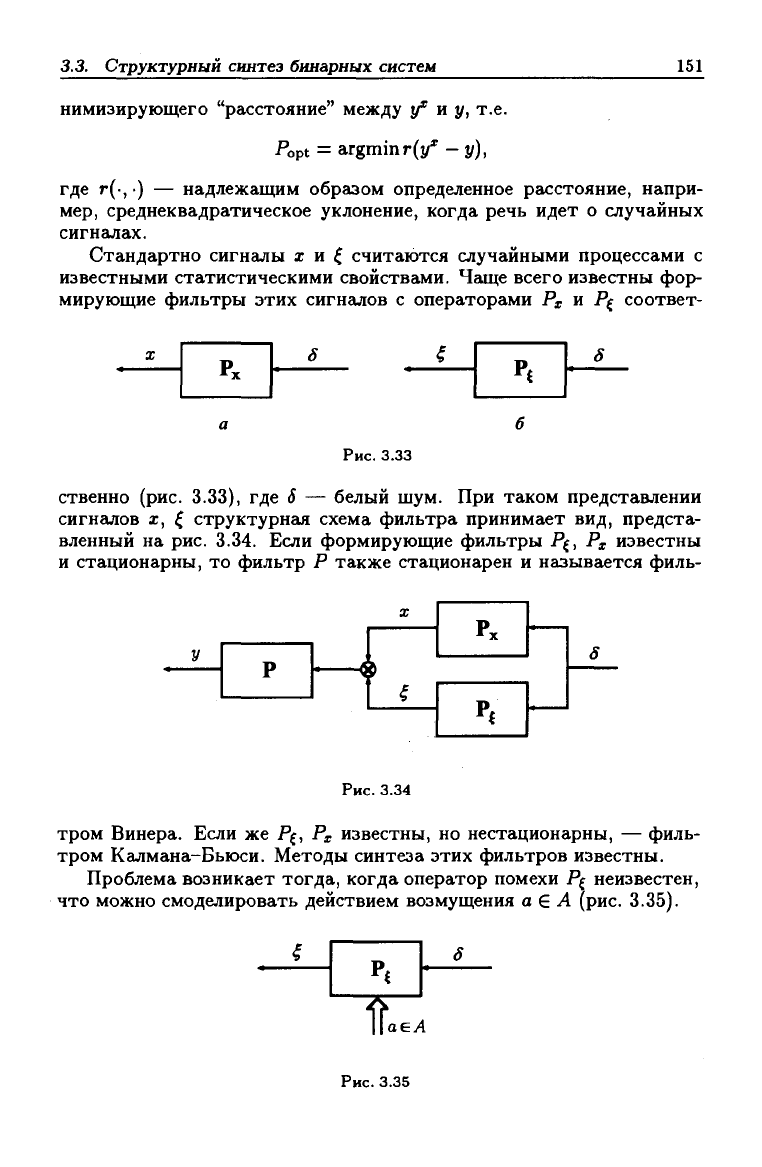
известными статистическими свойствами. Чгице всего известны фор-

мирующие фильтры этих сигналов с операторами Рх и Р( соответ-

Рис.

3.33

ственно (рис. 3.33), где S — белый шум. При таком представлении

сигналов X, ^ структурная схема фильтра принимает вид, предста-

вленный на рис. 3.34. Если формирующие фильтры Р(, Р^ известны

и стационарны, то фильтр Р также стационарен и называется филь-

-9

Рис.

3.34

тром Винера. Если же Р^, Рх известны, но нестационарны, — филь-

тром Калмана-Бьюси. Методы синтеза этих фильтров известны.

Проблема возникает тогда, когда оператор помехи Р( неизвестен,

что можно смоделировать действием возмущения а £ А (рис. 3.35).

еА

Рис.

3.35

152

Глава 3. Теории новых

типов обратной

связи

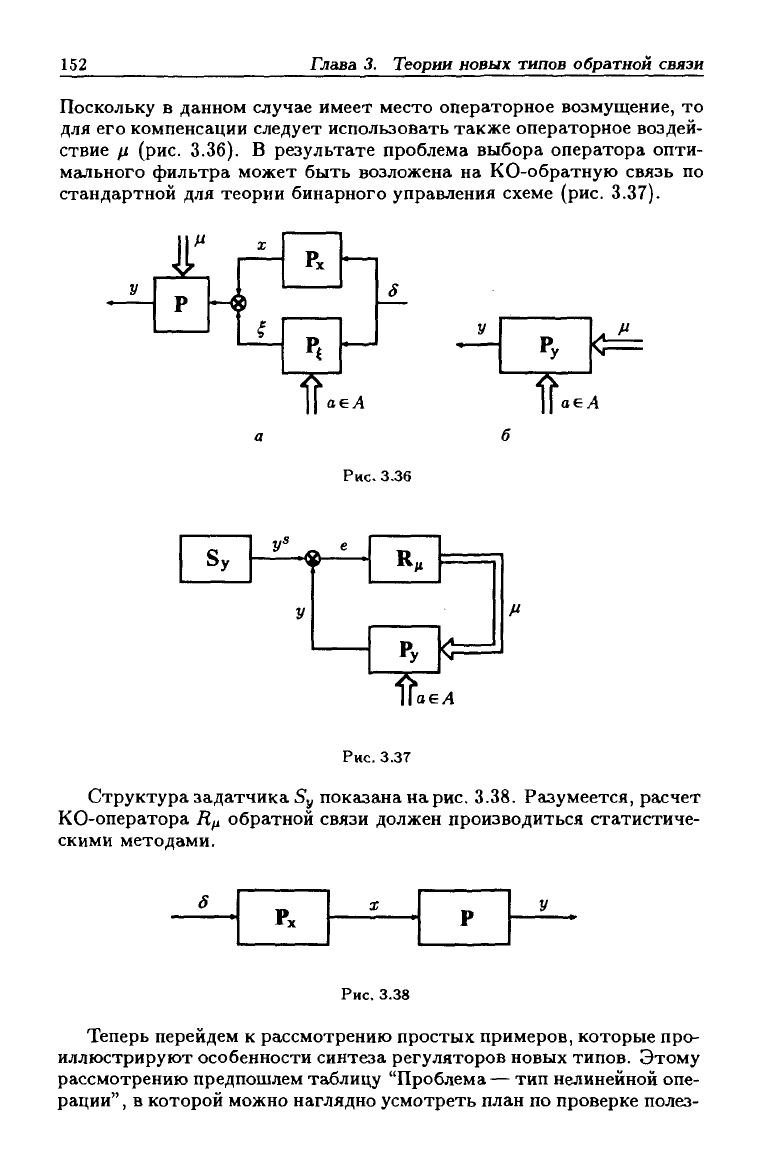
Поскольку в данном случае имеет место операторное возмущение, то

для его компенсации следует использовать также операторное воздей-

ствие /л (рис. З.Зб). В результате проблема выбора оператора опти-

мального фильтра может быть возложена на КО-обратную связь по

стандартной для теории бинарного управления схеме (рис. 3.37).

Рх

i'i

т^

еЛ

оеЛ

Рис.

3.36

'" б

•

Нд

/*—'

^j—'

¥а

еА

Рис.

3.37

Структура задатчика 5у показана на

рис.

3.38. Разумеется, расчет

КО-оператора Л^, обратной связи должен производиться статистиче-

скими методами.

Рис.

3.38

Теперь перейдем к рассмотрению простых примеров, которые про-

иллюстрируют особенности синтеза регуляторов новых типов. Этому

рассмотрению предпошлем таблицу "Проблема — тип нелинейной опе-

рации"

в которой можно наглядно усмотреть план по проверке полез-

3.3.

Структурный синтез

бинарных

систем

153

ности изложенной выше конструкции на стандартных задачах теории

управления.

Проблема

Стабилизация

Фильтрация

и дифференцирование

Оптимальность

Инвариантность

Тип нелинейной операции

Унарная Бинарная

Заштрихованный столбец таблицы отражает достижения класси-

ческой теории регулирования, в которой бинарная операция не ис-

пользовалась активно. Достоинства и недостатки получаемых при

этом результатов упоминались выше. Во втором столбце таблицы

клетки не заштрихованы, и еще предстоит разобраться, что нового

дает принцип бинарности для решения этих задач.

Глава 4

Теория координатно-операторной

обратной связи

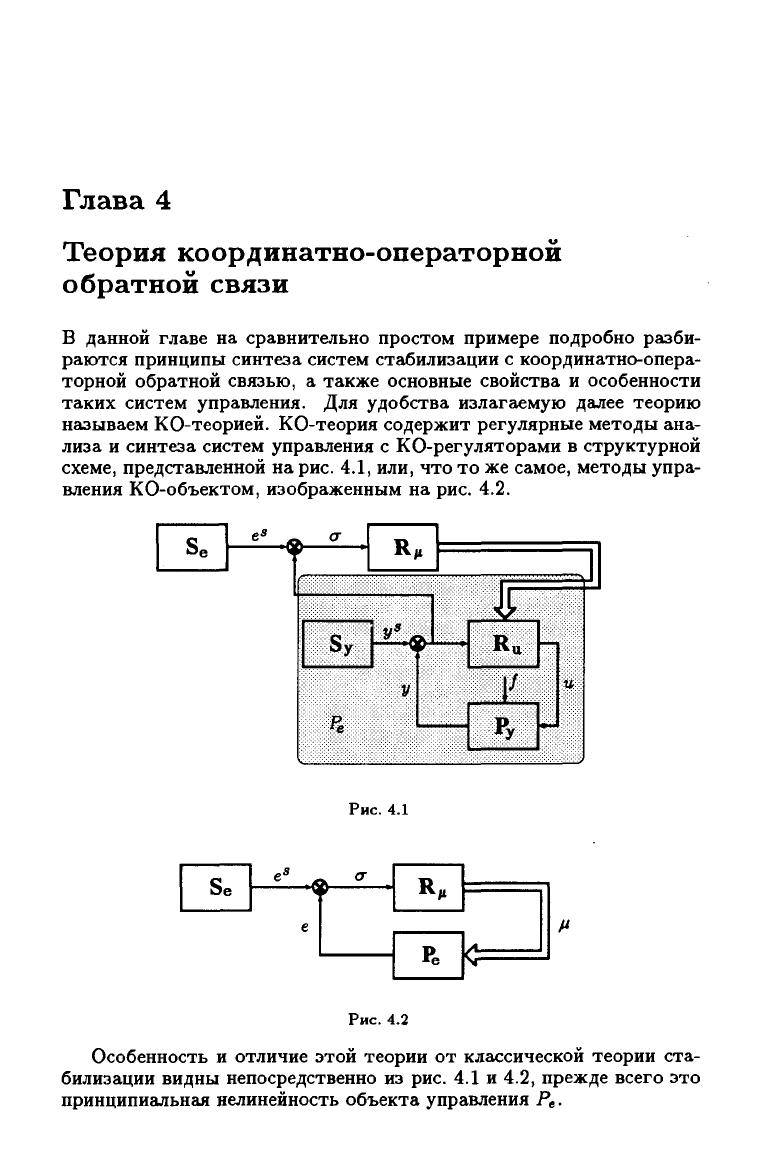
в данной главе на сравнительно простом примере подробно разби-

раются принципы синтеза систем стабилизации с координатно-опера-

торной обратной связью, а также основные свойства и особенности

таких систем управления. Для удобства излагаемую далее теорию

называем КО-теорией. КО-теория содержит регулярные методы ана-

лиза и синтеза систем управления с КО-регуляторами в структурной

схеме, представленной на рис.

4.1,

или, что то же самое, методы упра-

вления КО-объектом, изображенным на рис. 4.2.

>3е

е« _

-ч

«•М

•^

*е

Рис.

4.1

iff-

Рис.4

К,

Ре

Г"

Ru -

Ру •

/•

Ч|

Особенность и отличие этой теории от классической теории ста-

билизации видны непосредственно из рис. 4.1 и 4.2, прежде всего это

принципиальная нелинейность объекта управления Ре-

4.1.

Стабилизация объекта второго

порядка 155

Следовательно, стандартные методы синтеза обратной связи не-

применимы и нужно искать новые подходы. Продемонстрируем по-

лезность и конструктивность использования для этой цели изложен-

ных в предыдущей главе принципов генерации и бинарности новых

типов обратных связей.

4.1.

Стабилизация объекта второго порядка

с неизвестными параметрами

и внешним воздействием

Рассмотрим простейший объект второго порядка Е'':

XI = 12,

Х2 = axi+bu + f, (4.1)

y = CXi +Х2,

с неизвестными параметрами а, 6 и возмущением /, удовлетворяю-

щими включениям

аеА = {а\\а\<ао},

е В = {Ь \0 <Ь- <Ь <Ь+},

/eF*='{/|l/l</m},

где числа оо, 6^ и функция /„ известны. Этот объект, называ-

емый далее Е^-системой, позволяет дать содержательный набросок

КО-теории, отражающий, практически без изъятий, ее основные по-

ложения и результаты.

В задаче стабилизации Е*"-системы требуется указать робастную

гладкую обратную связь по состоянию, стабилизирующую Е^-систему

при произвольном изменении параметров а £ А, Ь £ В и любом воз-

мущении f Е F.

Из предшествующего изложения совершенно ясно, что стандарт-

ные подходы к этой задаче не гарантируют ее решения, ибо:

• глубокая обратн£1Я связь неробастна;

• адаптивное управление неприменимо, так как не выполнены основ-

ные условия: квазистационарность параметров и действие исчеза-

ющего возмущения;

• методы СПС ориентированы на использование разрывного упра-

вления, когда робастность не достигается.

При синтезе КО-регулятора будем следовать рекомендациям об-

щей теории систем с новыми типами обратной связи, но прежде ука-

жем два полезных и сильно упрощающих дело нгьблюдения.

156 Глава 4. Теория

коордиматно-операторной обратной

связи

4.1.1.

Принцип скаляриэации и уравнение объекта

в пространстве ошибок

Этот принцип позволяет при естественных условиях и при выполне-

нии МС-условия (т.е. условия согласованности возмущения) свести

задачу стабилизации многомерного объекта к задаче стабилизации

скалярного объекта.

Действительно, нетрудно убедиться, что выход Е^-системы экспо-

ненциально стремится к нулю (что и означает решение задачи ста-

билизации), если при некотором числе d >

обеспечено выполнение

связи

xi-|-rfxi=0. (4.2)

Величину

(Т

= ii + dXi

Х2 + dxi

назовем ошибкой реализации желаемой связи (4.2).

Теперь очевидно, что стабилизация ошибки

<т

в нуле и будет озна-

чать решение исходной задачи. Но отсюда еще не следует, что задача

стала скалярной. Для того чтобы убедиться в этом, перейдем от ис-

ходного пространства координат (xi,X2) к пространству ошибок —

координатам (xi,

<т).

Для этого находим сначала, что

О'

= XI -f dx\ =

Х2

-f dx2 = axi + bu -|- / -f dx2.

Из уравнения a =

+ dxi выражаем переменную X2:

X2 =

<T —

dxi.

В уравнениях S''-системы заменяем X2 найденным выражением. В

результате получаем искомые уравнения движения в виде

XI = -dxi +

(т,

(4.3)

&i=da+{a + d^)xi + bu + f. (4.4)

Уравнение (4.3) будем называть далее Ef-системой, а (4.4) — Е^-

системой. Из уравнений (4.3), (4.4) видно, что при <г —> О автома-

тически следует, что и xi

—*

0. Следовательно, для решения задачи

стабилизации можно ограничиться скалярным Ез-уравнением.

Если ввести обозначение

f = f + (a + d^)xr,

то указанными преобразованиями исходная проблема сводится к ста-

билизации скалярного Е2-объекта вида

dcr

+ bu + f, (4.5)

находящегося под воздействием неизвестного возмущения f Е F, для

которого известна только мажоранта

^={/|

\f\<{d^+ao)\xi\ + fm=fm}.

4.1.

Стабилизация объекта второго порядка

157

Поскольку уравнение

а — Х2 + dxi =

(4.6)

определяет прямую на плоскости (11,12)1 то геометрически принцип

скаляризации означает создание выбором управления условий, при ко-

торых прямая (4.6) является аттрактором, т.е. притягивающим ин-

вариантным множеством (рис. 4.3а). В пространстве ошибок этот

аттрактор превращается в одну из осей координат (рис. 4.36).

Рис.

4.3

Сделаем ряд замечаний, касающихся сведения общей задачи ста-

билизации к скалярной задаче и связанных с ней проблем управления

скаляризованным объектом Ej вида (4.5).

4.1.2.

Некоторые замечания

к постановке задачи и ее обобщения

При скаляризации задачи стабилизации необходимо иметь ввиду сле-

дующее.

Замечание 1. Рассмотрение объекта только с двумя неизвестными

параметрами а £ А, b G В

XI = Г2,

Х2 = axi +bu + f

нисколько не огргшичивает общности результата, так как уравнениям про-

извольного объекта с тремя неизвестными параметрами

Xl = Х2,

Х2 = aiXi + 02x2 •^Ьи + f,

где oi £ Ai, 02 € А2, Ь £ В, следующей нестационарной заменой перемен-

ных:

XI = C{t)zi, Z2 = il,

158 Глава 4. Теория координатно-операторной обратной связи

можно придать требуемый в рассматриваемой постановке задачи вид

ij = Zz\ +bu+ f.

Здесь

~ c + ojc + aic ~ Ь 7 /

« -с ^=c' •^=7'

если только c(t) — решение дифференциального уравнения

2с+020 = 0.

Замечание 2. Принцип скаляризации применим к Тфоизвольным объ-

екта общего положения с одним входом и одним выходом, т.е. к объектам

вида

Xi = Xi+i, 1=1, ...,n — 1,

Xn= Yl

<»'

^i +

+ /. y= ex.

Ы1

Действительно, в дгшном случае достаточно выбрать новую ошибку в виде

п-1

<г

= х„+ /_]<i,- Xi, di = const > О,

и в (n

—

1)-м уравнении D-системы заменить х„ на выражение

п-1

х„ =

—

У di

<r,

isl

a вместо последнего ургшнения в Е-системе записать уравнение

<т

= (dn-i -а„)<т+ ^J"*'^' + " + /•

ISl

в результате получим две подсистемы: Ei-систему (п

—

1)-го порядка

Xi = xi+1,

«'

= 1, ... ,п

—

х„_1 =

—

^ diXi + <т,

isl

и скалярную Ез-систему

сг

= dir +

+ f, у = с'х + Спв,

где х' = col («1, ...

in-i), с = (с', с„). При этом, если параметры di таковы,

что El-система при

<г

Xi = Xi+i, • = 1,

•

•. , п

—

Хп-1 = — Х^ diXi

isl

экспоненциально устойчива, то вновь из условия

<т

-f

следует, что Xi -+ О,

что является формгкльным выражением принципа скаляризации.

4.1.

Стабилизация объекта второго порядка

159

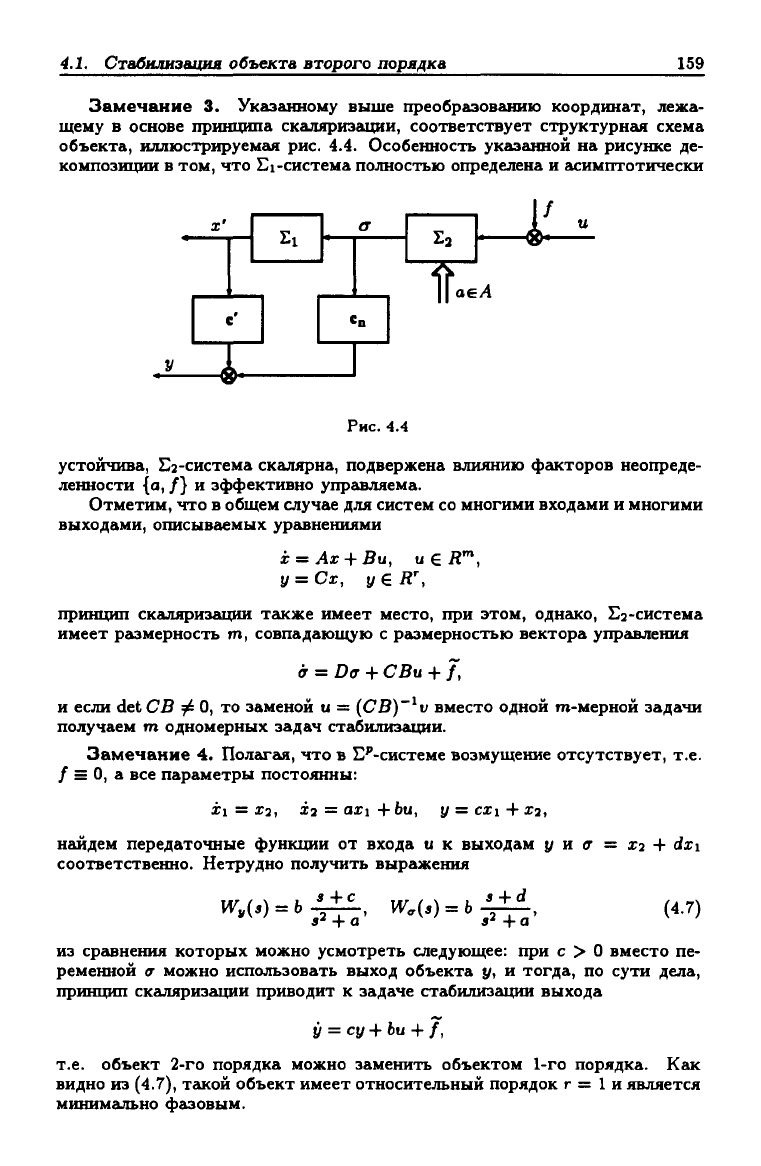
Замечание 3. Указанному выше преобразованию координат, лежа-

щему в основе принципа скаляриэации, соответствует структурнгья схема

объекта, иллюстрируемая рис. 4.4. Особенность указанной на рисунке де-

композиции в том, что El-система полностью определена и асимптотически

1ГабЛ

Рис.

4.4

устойчива, Ез-система скалярна, подвержена влиянию факторов неопреде-

ленности {а, /} и эффективно упргшляема.

Отметим, что в общем случае для систем со многими входами и многими

выходами, описываемых уравнениями

х = Ах + Ви,

е Д"*,

У = Сх, у € Д^

принцип скгшяризации также имеет место, при этом, однако, Ег-система

имеет размерность т, совпадающую с размерностью вектора управления

* = Dff + СВи

и если detCB ф О, то заменой и = (CB)~'f вместо одной т-мерной задачи

получаем m одномерных задач стабилизации.

Замечание 4. Полагая, что в E''-системе возмущение отсутствует, т.е.

/ = О, а все параметры постоянны:

ii=X2,

X2=axi-|-6u, 5/ = cxi+X2,

найдем передаточные функции от входа и к выходам у и (г = xj Ч- dx\

соответственно. Нетрудно получить выражения

^''(') = ЬЙ7- И'.(5) = Ь^

«2 +а'

a^-l-a

(4.7)

из сравнения которых можно усмотреть следующее: при с > О вместо пе-

ременной а можно использовать выход объекта у, и тогда, по сути дела,

принцип скаляриэации приводит к задаче стабилизации выхода

у = су

-I-

Ьи -f- /,

т.е.

объект 2-го порядка можно заменить объектом 1-го порядка. Как

видно из (4.7), такой объект имеет относительный порядок г = 1 и является

минимально фгкзовым.

160 Глава 4. Теория координатно-операторной обратной связи

Замечание 5. Выбор обратной связи, стабилизирующей Е^-объект:

а = da +

Ъи

+ f,

особенно прост, когда имеется полная информация о параметрах и возму-

щениях. В самом деле, при этих предположениях управление и = t;

—

f/b

сводит задачу стабилизации к тривиальной

= dff + V,

когда выбор управления t; очевиден. Если же параметры или возмущение не-

известны, то проблема становится сложнее, так как методы стабилизации

классической теории регулировгшия: глубокая обратнг^я связь (и = —fcu,

—>

оо), адгштивная обратная связь (и = —ка, к = la^, f = const > 0), си-

стема переменной структуры (и = —fm sgntr), при известных достоинствах

имеют недостатки и ограничения по применению.

Замечание 6. Покажем, что линейная обратная связь

u =

—k2<T —

kix\ (4.8)

с ограниченными коэффициентами годится для стабилизгщии свободных

движений неопределенного объекта с постоянными априорно ограничен-

ными параметрами (названного ранее интервальным объектом)

(Г

d<T

+ Ьи + (а - d^)xi, (4.9)

но,

вообще говоря, не решает задачи при изменении параметров а, Ь или

при наличии внешнего возмущения

= d(r + bu +

{a-d^)xi+f,

F. (4.10)

Действительно, после подстановки (4.8) в (4.9) и при f =

получим

& = {d-bk2)(T + {a-d^-bki)xi, (4.11)

и для анализа асимптотики

(т{1)

это уравнение следует дополнить уравне-

нием для ошибки II, т.е.

xi =

-dxi+iT.

(4.12)

Характеристический полином замкнутой системы (4.11) и (4.12) дается

выражением

det

s + d -1

bki -a +

d'^

s + bki -d

= s^ +bk-iS-\-bki -a + dbk2 =0,

и ясно, что при выполнении следуюхцих условии

к2>0, b~ki+db~k2> а~ (4.13)

замкнутая система асимптотически устойчива.

При изменении параметров условия (4.13) уже не гарантируют устойчи-

вость системы, а действие возмущения даже 1фи устойчивости свободных

движений не гарантирует стабилизируемости.