Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

4.1.

Стабилизация

объекта второго

порядка

161

Но даже при постоянных параметрах и / =

качество переходных про-

цессов может сильно варьироваться с изменением параметров и не соответ-

ствовать предъявляемым к системе требованиям.

Таким образом, может быть сформулирована следующая проблема:

•

как добиться независимости свойств замкнутой системы от факто-

ров неопределенности при ограниченных коэффициентах передачи

в каналах обратной связи?

4.1.3.

Фазовое пространство координата—оператор

Принцип скаляризации тесно связан с новыми типами обратной связи

и принципом бинарности. Именно, если переменную <г взять в каче-

стве ошибки КО-контура регулирования и использовать КО-обратную

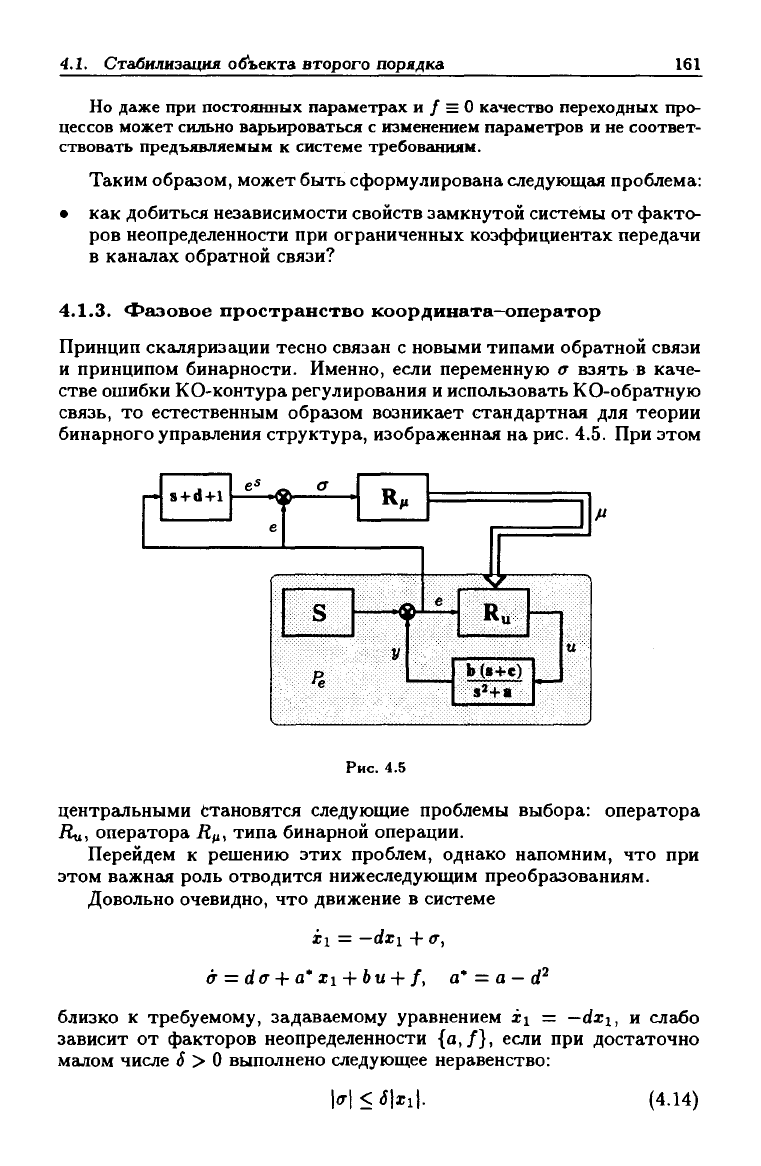
связь, то естественным образом возникает стандартная для теории

бинарного управления структура, изображенная на рис. 4.5. При этом

s+d+l

е«

Ре

К;,

•

б^

Л7

b (s+c)

•t

Рис.

4.5

центральными Становятся следующие проблемы выбора: оператора

R^,

оператора Д^, типа бинарной операции.

Перейдем к решению этих проблем, однако напомним, что при

этом важная роль отводится нижеследующим преобразованиям.

Довольно очевидно, что движение в системе

xi = —dxi -f-

(Г,

& =

d<r

+ a*xi + bu + f, а* = а

—

(Р

близко к требуемому, задаваемому уравнением xi = —dxx, и слабо

зависит от факторов неопределенности

{а,/},

если при достаточно

мгшом числе S >

выполнено следующее неравенство:

\<T\<SW\.

(4.14)

162

Глава 4. Теория

коордииатио-операторной обратной

связи

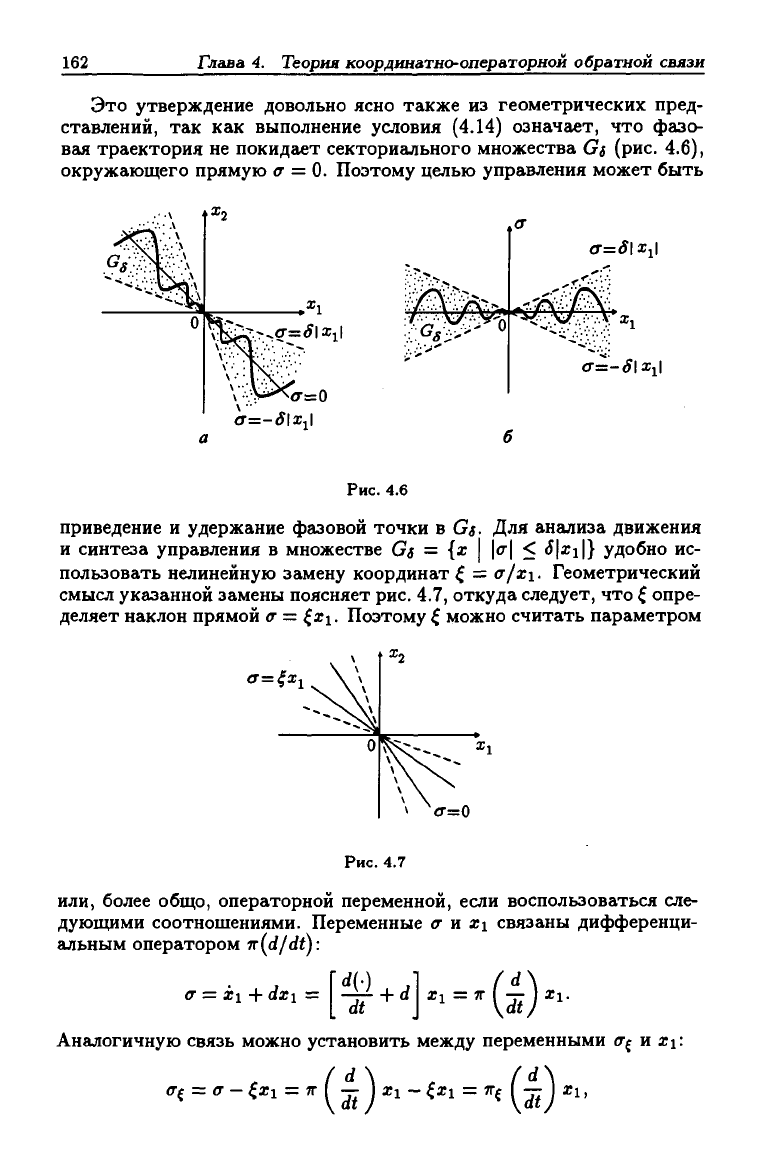
Это утверждение довольно ясно также из геометрических пред-

ставлений, так как выполнение условия (4.14) означает, что фазо-

вая траектория не покидает секториального множества d (рис. 4.6),

окружающего прямую (т = 0. Поэтому целью управления может быть

<T=S\x^\

q=.S\x^\

<T=-J| Xjl

Рис.

4.6

приведение и удержание фазовой точки в Gg- Для анализа движения

и синтеза управления в множестве Gs = {х \

\сг\

< S\xi\} удобно ис-

пользовать нелинейную замену координат ^ =

(T/XI.

Геометрический

смысл указанной замены поясняет рис. 4.7, откуда следует, что ^ опре-

деляет наклон прямой

(т

= ^xi. Поэтому ^ можно считать параметром

<т=4х

Рис.

4.7

или, более общо, операторной переменной, если воспользоваться сле-

дующими соотношениями. Переменные

и xi связаны дифференци-

альным оператором ir(d/dt):

(т

^ xi

-\-

dx\ =

•¥d

='Ш

х\.

Аналогичную связь можно установить между переменными а^ и xi:

4.1.

Стабилизация объекта второго порядка

163

где

'^^

(л) = Л

+ d-C

Поскольку ^ определяет оператор К(, то ее уместно ншвать опера-

торной переменной. Следовательно, пространство (xi,^) можно на-

звать фазовым пространством координата-оператор, или, коротко,

КО-пространством. Какую же пользу можно извлечь из указанной

замены переменных?

Для ответа на этот вопрос достаточно найти уравнение изменения

новой переменной ^ =

(T/XI.

Положим пока, что / = О, тогда имеем

последовательно:

• _ (т (Г XI _

dcr

Ьи

+ a*xi а а

—

dx\ _

Xl Xi Xi Xi Xi Xl

Если теперь ввести обозначение ц = и/хх и назвать /i новым управле-

нием, то проблема стабилизации свободного движения параметриче-

ски неопределенного объекта

<т

cf(T

-f a'xi + bu

сводится к проблеме стабилизации определенного объекта, находяще-

гося под воздействием координатного возмущения а*, так как теперь

мы имеет дело с уравнением Е{ вида

^di-ai-d) +

b^L

+ a\

Иными словами, путем нелинейной замены ^ = (T/XI сложная про-

блема стабилизации неопределенного Е^-объекта (рис. 4.8а,б) транс-

формирована в хорошо изученную проблему компенсации координат-

ного возмущения для Е{-объекта (рис. 4.8в). Обсуждению и сравне-

Г?

абЛ

06/1

Рис. 4.8

нию вариантов выбора управления fi на основе стандартных приемов

компенсации посвящена последующая часть параграфа, а здесь от-

метим, что, хотя принципиально проблема синтеза стабилизирующей

164 Глава 4. Теория

координатио-операторной обратной

связи

обратной связи решена, сложности все-таки неизбежны, так как при-

менение известных принципов должно проходить в новых условиях,

поскольку объект принципиально нелинеен:

XI = ~dxi+^xi,

be В,

а*

еА*.

Ввиду того что эти уравнения действуют на множестве Gs,

6 мало,

второе уравнение можно линеаризовать и, без больших потерь в общ-

ности, ограничиться рассмотрением уравнения первого приближения

Завершг1Я этот раздел, заметим, что в ходе преобразования коор-

динат было введено следующее обозначение:

/*= —.

которое, по сути дела, задает статическую бинарную операцию

u = l3{ii,xi) =ЦХ1,

определяющую оператор Д„ координатной обратной связи в струк-

турной схеме на рис. 4.5.

Разумеется, это не единственная, но, быть может, простейшая воз-

можность. Можно было бы использовать и динамическую бинарную

операцию, например операцию интегрального

XI J

fidt

или инерционного типа

•//xrft, г =

(

— =zT/i+ I ftdt,

= const.

в любом случае общие выводы, конечно, сохраняют силу, однако

вместо скгиярного объекта пришлось бы иметь дело с объектом более

высокого порядка, например, при интегральной бинарной операции

стабилизируемая система описывается системой уравнений

i = 2d^ + bni + a', fii=zfi.

4.2.

КО-алгоритмы стабилизации

Воспользуемся стандартными методами классической теории регули-

рования для синтеза управления, стабилизирующего скалярный объ-

ект:

i = 2d^ +

b^i

+ a-d\ (4.15)

а ел, be В, d>Q.

4.2. КО-алгоритмы

стабилизации

165

4.2.1.

Прямая компенсация

В уравнении (4.15) параметр d^ можно интерпретировать как извест-

ное возмущение, и при известном параметре 6 с помощью прямой ком-

пенсации

= ^l + — (4.16)

влияние этого "возмущения" устраняется, ибо

i=2d^

+ bfii + а.

Если же параметр 6 неизвестен, то прямая компенсация в "лоб" не

проходит, но ее можно успешно сочетать с идентификацией параме-

тров.

Об этом скажем чуть позже, а сейчас заметим, что управлению

(4.16) в исходных переменных отвечает обратная связь вида

и = ЦХ1 =

1Л1Х1

+ -7-Xi,

имеющая бинарную и линейную составляющие.

Заметим, что если параметр а тоже известен, то необходимости в

бинарной компоненте не возникает.

4.2.2.

Асимптотическое оценивание

или косвенное измерение О-воэмущения

Рассмотрим вариант задачи стабилизации объекта

i = 2d^ + a + bfii, (4.17)

когда параметры а, Ь фиксированы, 6 известен, а — любой элемент

из А. Для получения оценки а неизвестного параметра а используем

наблюдатель

i = {2d-kl)<p-\-a + k,^ +

b^^,

а = —kiif

—

^), ^1,^2 = const.

После вычитания (4.17) из (4.18) и введения обозначений

е =

(р

—^, а z=a

—

с учетом

того,

что параметр о

фиксирован,

т.е.

а = 0,

получим уравнения наблюдателя относительно ошибок (е, а)

e = i2d-k.)e^a,

а = -«26. '

'Здесь и далее для простоты вместо а' = а

—

tfi пишем а, полагая, что компо-

нента d? уже скомпенсирована.

166 Глава 4. Теория

координатио-операторной обратной

связи

Характеристический полином наблюдателя (4.19) имеет вид

det

s-i2d-ki) -1

= £^ + s{ki

2d) +

Jfc2

= о

и является гурвицевым при выполнении неравенств Агг

О,

fci

2d.

Поэтому оценка а асимптотически (экспоненциально) сходится к чи-

слу а. Если теперь управление ц сформировать в виде

ti=Mi-j,

(4.20)

то произойдет асимптотическая компенсация возмущения а, так как

^ = 2d^ + bni +

о,

и, следовательно, а

—

—>

Таким образом, при выборе управления ^i достаточно иметь дело

со свободным движением объекта:

i = 2d^ + bfix.

В исходных переменных алгоритму управления (4.20) соответствует

алгоритм вида

/iXi

filXi

-Xi,

где вторую компоненту естественно называть адаптивной. Иными

словами,

• описанный способ асимптотического оценивания постоянного воз-

мущения а реализует стандартную процедуру адаптивного упра-

вления.

Если, однако, а

а(<), то теория адаптивного управления не дает

рекомендаций по синтезу стабилизирующего управления, тогда как

развиваемая теория легко переносится на этот случай.

4.2.3.

Компенсация волнового О-возмущения

Пусть известен дифференциальный оператор К (d/dt), аннулирующий

0-возмущение, т.е.

.(i),.o.

Например, известны числа г, р такие, что

а+ра + г = 0, (4.21)

но неизвестно начальное условие а(0), что делает возмущение а неиз-

вестным.

4.2. КО-алгоритмы

стабилизации

167

Согласно рекомендации кл£1Ссической теории регулирования при

стг1билизации объекта

i = 2d^ + bn + a (4.22)

следует по уравнениям (4.21), (4.22) составить уравнения наблюда-

теля, вырабатывающего асимптотическую оценку а возмущения а.

Такой наблюдатель строится стандартным образом и имеет вид

а = —ра - г

— к2(<р

- <).

После почленного вычитания (4.21) и (4.22) из (4.23) и перехода к

ошибкам оценивания

е =

(fi —

^, а = а

—

уравнения наблюдателя принимают вид

е = (2^-Ые + а,

а = —ра

—

«ге.

Характеристический полином системы (4.24) дается выражением

det

+ (fei - 2d) -1

Аз S + р

= s^ + (p + ki- 2d)s + к2+ p{ki - 2d) = О,

и ясно, что наблюдатель экспоненциально устойчив, когда

ki>2d-p, k2>p{ki-2d).

Последнее условие легко выполнить, и, следовательно, наблюдатель

(4.24) дает асимптотическую оценку

~ ехр

а—^а.

В силу полученной асимптотической оценки управление

peuieieT задачу компенсации переменного возмущения a(t) и сводит

исходную задачу стг^билизации к тривиальной задаче стабилизации

объекта

^ = 2de + 6^i.

Отметим, что аналогичный результат невозможно получить, дей-

ствуя в рамках стандартной концепции адаптивного управления.

168

Глава

Теория коордииатио-операторной обратной связи

4.2.4. Релейная К О-стабилизация

При отсутствии волновой модели 0-возмущения, но при известной ма-

жоранте а°, т.е. такой функции или постоянной, что

\a{t)\<a°,

для стабилизации объекта

возможно применение разрывной, в частности, при а° = const, релей-

ной обратной связи

И = -*sgn^.

Тогда замкнутая система описывается уравнением

^ = 2d^

—

к sgn ^ + а, к = const

и при выполнении условия

(4.25)

к>а°

существует окрестность, в которой нуль уравнения (4.25) асимптоти-

чески устойчив.

Представление о качественном поведении решений уравнения

^ = 2d^-ksgn^ + a (4.26)

можно получить из рис. 4.9а, изображающего многообразие решений

уравнения (4.26), или рис. 4.96, на котором показан ход фазовых тра-

екторий в КО-пространстве (iCi,^). Скользящий режим в релейной

к+а

Скользящий

режим

' ~

-S

-к+а

Рис.

4.9

системе не является прочным и "размывается" до реального скользя-

щего режима при введении пространственной задержки Д или малого

запаздывания в переключения, т.е. если вместо (4.26) мы имеем дело

с уравнениями вида

^ = 2d^-A:sgnд^^-a, ^ = 2di - ksgn^^ + а.

(4.27)

4.2.

КО-етгоритмы стабилизация

169

Сказанное иллюстрируют рис. 4.10, где Д(г) — "амплитуда" ре-

ального скользящего режима. Все отмеченные свойства релейной си-

стемы хорошо известны и ранее уже отмечались. Сейчас же гораздо

Рис. 4.10

интереснее посмотреть на то, какие движения в исходном координат-

ном пространстве {xi, гг) соответствуют указанным выше движениям

в КО-пространстве (ii,^).

Сначала сделаем это формально, использовав первое уравнение

объекта в переменных (xj,^), т.е. уравнение

XI = -dxi + ^ari = -{d - i)xi.

При возникновении идеального скользящего режима имеет место ра-

венство ^ =

и, следовательно, переменная х\, а вместе с ней и выход

объекта у экспоненцигиьно убывают до нуля, так как xi =

—dxj.

режиме реального скольжения выполняется условие |^| < Д < J и

также имеет место экспоненциальная устойчивость, если S < d, что,

конечно, выполнено. Поэтому полученная система бинарного управле-

ния с релейным КО-алгоритмом экспоненциально устойчива как при

идеальных, так и при реальных переключениях. Иначе говоря,

• она прочна по отношению к неидеальностям в переключениях, при-

чем не только временного, но (!) и пространственного типа.

Можно сказать, что прочностные свойства нелинейной разрывной

системы зависят от места расположения в ее структуре разрывного

(релейного) элемента.

Рассмотрим теперь построенную бинарную систему с релейным

КО-алгоритмом стабилизации в исходном координатном простран-

стве (х1,хч). Поскольку и = /ХГ1, а — ^xi, ^ = —fcsgn^, то имеем

последовательно

и — —кxisgn ^ = —кxisgn — — —к\х\\sgn

(т.

(4.28)

170

^лава 4. Теория

координатно-операторной обратной

связи

Распространим действие этого алгоритма управления за пределы

множества Gs на всю плоскость (2:1,12), тогда этот алгоритм стано-

вится стандартным алгоритмом управления систем переменной струк-

туры. Действительно, последнее выражение в (4.28) определяет стан-

дартную V'-ячейку:

f -к, Х1(г> О,

и = фХ1, Ф=< , ^о

[ к, xiff < О,

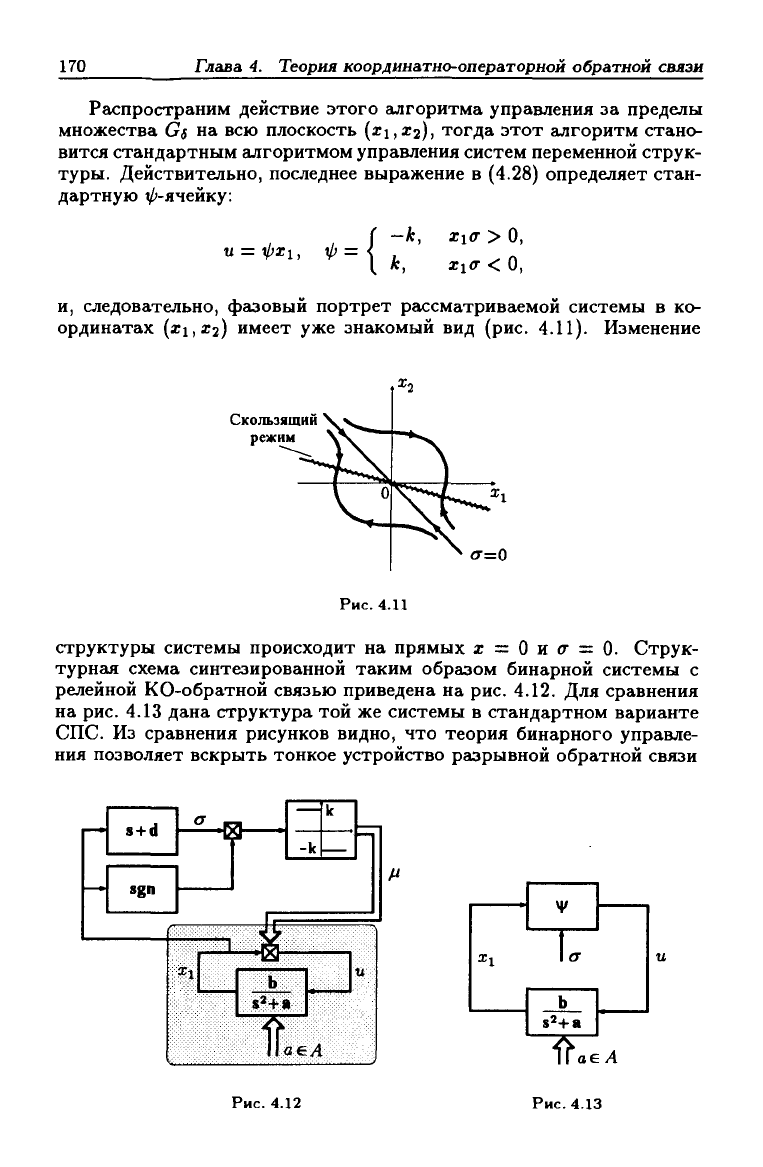
и, следовательно, фазовый портрет рг1СсматриБаемой системы в ко-

ординатах (xi,X2) имеет уже знакомый вид (рис. 4.11). Изменение

Скользящий

режим

<т=0

Рис.

4.11

структуры системы происходит на прямых а; = О и (Т = 0. Струк-

турная схема синтезированной таким обргьзом бинарной системы с

релейной КО-обратной связью приведена на рис. 4.12. Для сравнения

на рис. 4.13 дана структура той же системы в стандартном варианте

СПС.

Из сравнения рисунков видно, что теория бинарного управле-

ния позволяет вскрыть тонкое устройство разрывной обратной связи

s + d

sgn

°' IT

'12

-к

•I2SI

Рис. 4

аеА

.12

Xi Iff

1>ав

Рис. 4.13