Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

4.2. КО-ллгоритмы стабилизации

171

и, следовательно, представляет возможности регулярного синтеза та-

кой обратной связи, тогда как в теории СПС вид обратной связи был

угадан. Еще одна принципиальная особенность КО-обратной связи —

ее знакопеременность в зависимости от положения фазовой точки на

плоскости. Формально это следует из формулы

и = fiXi = —^|ii|sgn (Т,

следовательно, fi = —ksgn{xia). Иными словами,

• работоспособность систем с КО-связью достигг1ется только при

переменности структуры системы.

4.2.5. Замечание о прочности систем с релейной КО-связью

Между классической СПС и изучг1емой бинарной системой управления

есть,

однако, принципиальное различие, которое проявляется при на-

личии неидеальностей в переключениях. Именно, в бинарной системе

при появлении временной или пространственной задержки в пере-

ключениях выполнено неравенство |^| < Д и, следовательно, асимпто-

тическгш устойчивость сохраняется, а фазовый портрет имеет вид,

показанный на рис. 4.14а. Для стандартной СПС при временной за-

держке переключения фазовый портрет совпадает с портретом на

Рис.

4.14

рис.

4.14а, но при пространственной задержке отличается от него и

имеет вид, указанный на рис. 4.145. Следовательно,

• бинарная система управления, замкнутая КО-релейной обратной

связью, прочна по отношению к этим возмущениям,

тогда как классическая СПС не является прочной. Таким образом,

показано, что при отсутствии волновой модели 0-возмущения а, т.е.

\а\ < а", и любом 0-возмущении 6 > 6min > О, т.е. Ь £ В, синтези-

рованный алгоритм бинарного управления с КО-релейной обратной

связью

• пока единственный из известных робастно решгьет задачу стг1би-

лизации неопределенного нестационарного объекта.

Это и есть первый практический "выход" КО-теории стабилизации.

172 Глава 4. Теория

коордииатно-операториой обратной

связи

Одним из недостатков рассмотренного алгоритма является нали-

чие "биений", сопровождающих режим релейного скольжения, в кото-

ром фунционируют, конечно, все физические системы. Другой недо-

статок связан с трудоемкостью точной цифровой реализации сколь-

зящего режима в реальном времени, поскольку в этом случае можно

применять схемы аппроксимации только 1-го порядка, но тогда "ам-

плитуда" отклонения от линии скольжения имеет порядок шага дис-

кретизации Л, т.е.

М~о(л).

Поэтому важно иметь ответ на следующий вопрос:

• существуют ли непрерывные алгоритмы стабилизации, сообщаю-

щие замкнутой системе описанные выше свойства?

Пожалуй, ясно, что в общем случае ответ на этот вопрос отрицателен,

но в чгигтных случаях можно указать такие алгоритмы. Оставаясь

пока в рамках КО-теории, укажем некоторые из них.

4.2.6. Линейные КО-алгоритмы стабилизации

Рассмотрим ситуацию, когда при стабилизации объекта

^ = 2d^+bn + a

известные параметры а

Е^

А,Ь £ В можно считать постоянными. При

неизвестном 6 метод асимптотического оценивания неприменим и сле-

дует поискать иные приемы стабилизации. Такие приемы развиты в

классической теории регулирования, и они предполагают использо-

вание линейных обратных связей с интегральной компонентой: так

называемые ПИ- (пропорционально-интегральные) и ПИД- (пропор-

циональные интегрально-дифференциальные) законы регулирования.

По прежде рассмотрим пропорциональные законы.

П-законы регулирования. В этом случае

fi = —k^, к

—

const,

замкнутая система управления описывается уравнением

^ = -(bife-2d)^-|-a,

и при выполнении условия

6-fc>2cf

она асимптотически устойчива с положением равновесия в точке

4сс =

bit-2d

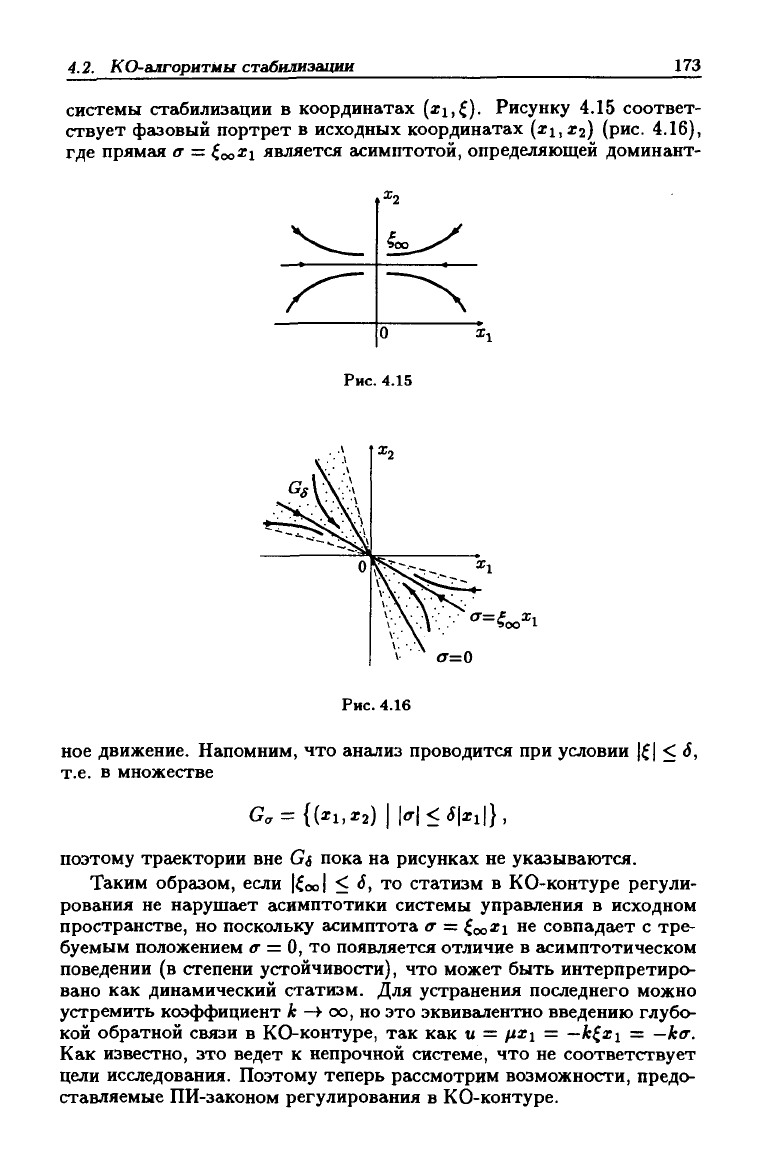
Фазовый портрет замкнутой системы управления в координатах

(«1,

^) приведен на рис. 4.15. Точка

^оо

на рисунке определяет статизм

4.2.

КО-алгоритМы стабилизации

173

системы стабилизации в координатах (xi,f). Рисунку 4.15 соответ-

ствует фазовый портрет в исходных координатах (xi,a:2) (рис. 4.16),

где прямая а

—

(,жХ\

является асимптотой, определяющей доминант-

Рис. 4.15

Рис. 4.16

ное движение. Напомним, что анализ проводится при условии \$\ < <J,

т.е.

в множестве

G<r = {(xi,X2) |H<<J|xi|},

поэтому трг1ектории вне d пока на рисунках не указываются.

Таким образом, если |^оо| < <5, то статизм в КО-контуре регули-

рования не нарушает асимптотики системы управления в исходном

пространстве, но поскольку асимптота а = ^ooXi не совпадает с тре-

буемым положением

<г

= О, то появляется отличие в асимптотическом

поведении (в степени устойчивости), что может быть интерпретиро-

вано как динамический статизм. Для устранения последнего можно

устремить коэффициент

А;

-> ос, но это эквивалентно введению глубо-

кой обратной связи в КО-контуре, так как « = \ix\ = —к(,х\ =

—к<т.

Как известно, это ведет к непрочной системе, что не соответствует

цели исследования. Поэтому теперь рассмотрим возможности, предо-

ставляемые ПИ-законом регулирования в КО-контуре.

174 Глава 4. Теория

координатно-операторной обратной

связи

ПИ-законы регулирования.

этом случае

Ii =

-k2^-ki Udt

(4.29)

и при замыкании такой обратной связью исследуемого объекта

i = 2d^ + bfi + a (4.30)

получалм систему управления второго порядка

^+{bk2-2d)i + bkii

(4.31)

Уравнение (4.31) получено

результате подстановки продиффе-

ренцированного соотношения (4.29)

продифференцированное урав-

нение (4.30).

Из

уравнения (4.31) ясно видно, что при выполнении

условий Ь~к2

2d,

fci >

наступает асимптотическая устойчивость

нуля уравнения. В зависимости от соотношений параметров

ki,

Лг эта

устойчивость может быть колебательной или апериодической. Кроме

этого, степень устойчивости также может быть назначена по произ-

волу надлежащим выбором параметров кх,

fcj-

На рис. 4.17 в координатах (^,^) изображены фазовые траектории,

отвечающие колебательным и апериодическим переходным процессам

в замкнутой системе

^ -f-

(6А2

—

2с/)^ +

bki^ = 0.

На рис. 4.18 при-

Рис. 4.17

.л

t*2

<т=0

Рис. 4.18

4.2.

КО-адгоритмы стабилизации

175

ведены соответствующие им проекции фазовых траекторий на плос-

кость (г1,а;2)-

Результирующий алгоритм стабилизации, отвечающий ПИ-закону

КО-обратной связи, имеет вид

и = fiXi =

—Л2 ^Xi —

kixi ^dt =

—к^ст —

kixi I —

J xi

(4.32)

dt.

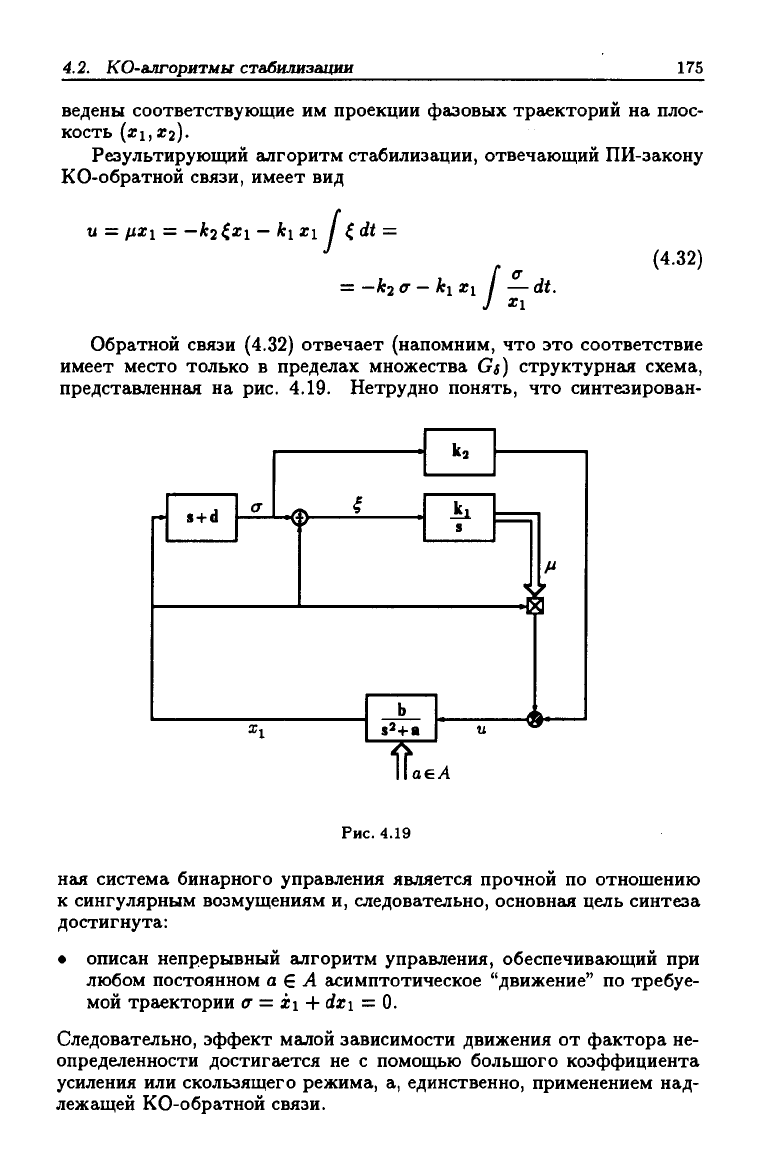
Обратной связи (4.32) отвечает (напомним, что это соответствие

имеет место только в пределах множества Gs) структурная схема,

представленная на рис. 4.19. Нетрудно понять, что синтезирован-

•• » + d

<т

J—

1 1

к.

]

Рис.

4.19

ная система бинарного управления является прочной по отношению

к сингулярным возмущениям и, следовательно, основная цель синтеза

достигнута:

• описан непрерывный алгоритм управления, обеспечивающий при

любом постоянном а € А асимптотическое "движение" по требуе-

мой траектории а = xi + dxi = 0.

Следовательно, эффект малой зависимости движения от фактора не-

определенности достигается не с помощью большого коэффициента

усиления или скользящего режима, а, единственно, применением над-

лежащей КО-обратной связи.

176

Глава 4. Теория

координатно-операторнои обратной

связи

4.2.7. Иятегрально-релейный КО-алгоритм стабилизации

Из структуры системы на рис. 4.19 видно, что для реализации ПИ-

закона в КО-контуре обратной связи необходимо использовать опера-

цию деления, от которой можно избавиться, если вместо интегральной

компоненты применять релейно-интегральную компоненту. Именно,

исследуем последствия, наступающие при законе

fi = -.k2^-ki / Sgn^rft.

В этом случае поведение замкнутой системы определяется уравнением

^+{bk2-d'^)i + bkisgni = 0. (4.33)

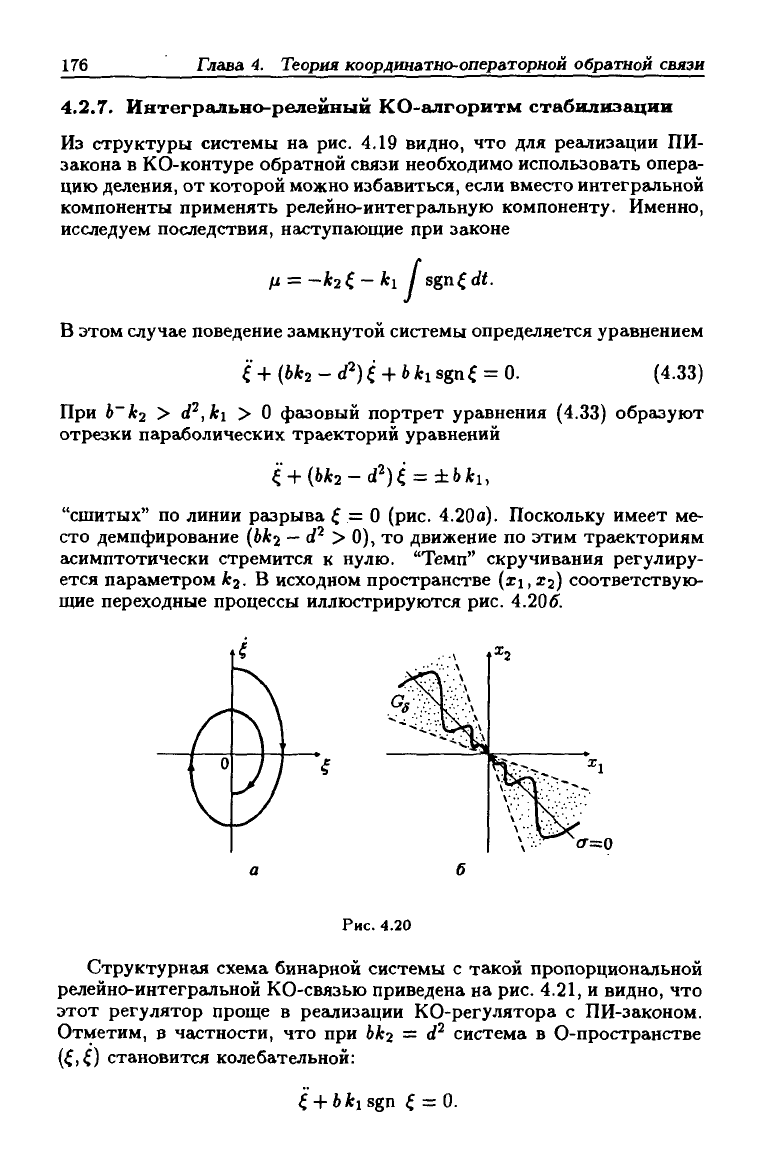
При Ь~к2 > d'^,ki > О фазовый портрет уравнения (4.33) образуют

отрезки параболических траекторий уравнений

{bk2-d'')i^±bkx,

"сшитых" по линии разрыва ^ =

(рис. 4.20а). Поскольку имеет ме-

сто демпфирование (бАгг

—

<f^ > 0), то движение по этим траекториям

асимптотически стремится к нулю. "Темп" скручивания регулиру-

ется параметром ^2- В исходном пространстве (х\,Х2) соответствую-

щие переходные процессы иллюстрируются рис. 4.205.

.л

. ••••••• л

>*Г^.

с^-Шл

.Xj

fe.~^^ X

*'.':'^' •.••••••.'•'.

•• •

1. л.'- •'

\ •VV/jir

\:>^сг=

Рис.

4.20

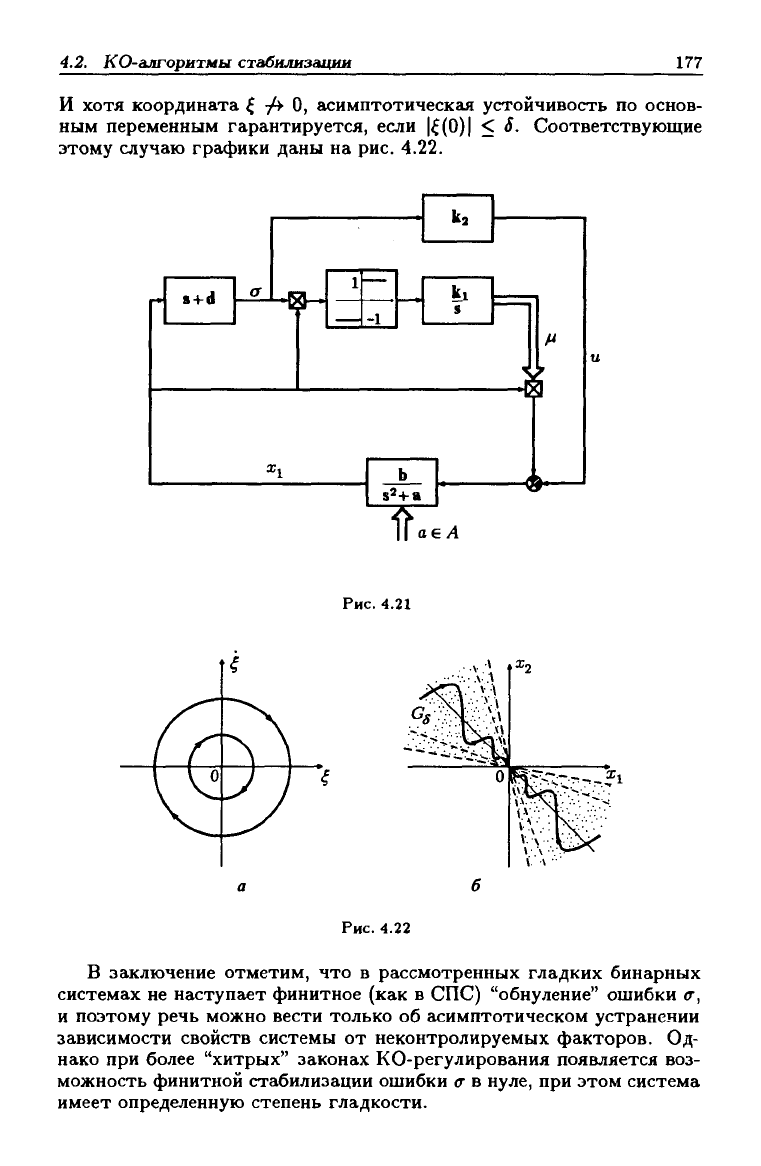
Структурная схема бинарной системы с такой пропорционгшьной

релейно-интегральной КО-связью приведена на рис. 4.21, и видно, что

этот регулятор проще в реализации КО-регулятора с ПИ-законом.

Отметим, в частности, что при бАгг = d^ система в 0-пространстве

{^,i) становится колебательной:

^-l-6*isgn ^ = 0.

4.2.

КО-аиггорнтмы стабилизации

177

И хотя координата ^ т^ О, асимптотическая устойчивость по основ-

ным переменным гарантируется, если

|^(0)|

< S. Соответствующие

этому случаю графики даны на рис. 4.22.

г> s-t-d

•\i

-1

+ «

к.

, '

<a-

Рис.

4.21

E'.fVr-.-

з;

Рис.

4.22

В заключение отметим, что в рассмотренных гладких бинарных

системах не наступает финитное (как в СПС) "обнуление" ошибки <г,

и поэтому речь можно вести только об асимптотическом устранении

зависимости свойств системы от неконтролируемых факторов. Од-

нако при более "хитрых" законах КО-регулирования появляется воз-

можность финитной стабилизации ошибки а в нуле, при этом система

имеет определенную степень гладкости.

178

Глава

Теория координатно-операторной обратной

связи

Более подробное обсуждение этих вопросов составляет предмет

следующих тем. Здесь же подчеркнем следующее:

• асимптотической независимости движения в системе управления

неопределенным объектом можно добиться без использования глу-

бокой обратной связи или скользящего режима, а только примене-

нием нелинейной обратной связи КО-типа. Это второй практиче-

ский результат КО-теории;

• физическая основа компенсации неопределенности состоит в ис-

пользовании на некоторых этапах движения положительной обрат-

ной связи, которая позволяет управляющему сигналу "нарасти" до

величины, достаточной для компенсации неопределенности. Это

происходит подобно тому, как описано в главе 2 при решении за-

дачи о воспроизведении задающего воздействия с помощью одного

интеграла.

Глава 5

Скользящие режимы высших порядков

Из предыдущего изложения видна та важная роль, которая принад-

лежит скользящему режиму в задачах управления в условиях неопре-

деленности. Достаточно вспомнить релейные системы, системы пе-

ременной структуры, системы с координатно-операторнои обратной

связью. Краткое исследование, проведенное в соответствующих раз-

делах монографии, показало, что при определенном сходстве имеется

глубокое различие в скользящих режимах, проявляющееся, в част-

ности, под воздействием факторов неопределенности и помех. Бо-

лее детальное исследование показывает, что существует много видов

скользящего режима и объединяет их только факт наличия разрывов

правой части дифференциальных уравнений, описывающих поведение

соответствующих динамических систем. Далее мы дадим содержа-

тельный набросок того раздела общей теории скользящих режимов,

который связан со степенью гладкости на рещениях системы функ-

ции, определяющей поверхность разрыва. Степень гладкости решения

естественным образом упорядочивает скользящие режимы, и появля-

ется возможность введения нового понятия — порядка скольжения.

5.1.

Некоторые предварительные сведения

из теории скользящего режима

Изложим некоторые факты из теории скользящих режимов, необхо-

димые для понимания дальнейшего изложения.

Скользящие режимы возникают в разрывных динамических систе-

мах, например в системах управления вида

X = /(х) +6(х)и,

где управление и (обратная связь) терпит разрывы на гладком мно-

гообразии

М = {г € Л" I

(т{х)

= 0} ,

именно:

•(г),

(7{x)>Q,

•(х),

(т(х)<0, и''фи-

Ф)={:-i

180 Глава 5. Скользящие

режимы

высших порядков

Скользящий режим имеет место в тех точках многообразия М, к

которым фазовые траектории х* (t) динамических систем

x = f^ix) = f{x)-\.b{x)u^ix)

подходят с разных сторон многообразия и трансверсально его пересе-

Vo-(x)

/+(х)

Рис.

5.1

кают (рис. 5.1). В таких точках выполнены следующие неравенства:

±(V.T(x),/±(x)>|^(,)=o<0.

Объединение всех таких точек х G М образует множество Msi С М,

нгаываемое далее областью скольжения (на рис. 5.1 она выделена).

5.1.1.

Уравнения скольжения

Для получения уравнений, описывающих движение в скользящем ре-

жиме (далее они называются уравнениями скольжения), можно ис-

пользовать процедуру Филиппова. Опишем необходимый фрагмент

этой процедуры. Соединим прямой концы фазовых векторов

f^{x).

Всякий вектор fa{x), упирающийся в эту прямую, дается выпуклой

комбинацией /„ = а/"*" -|- (1

—

oi)f~ фазовых векторов

/*(х).

Один из

этих векторов принимается за искомый (рис. 5.2). Именно, поскольку

/^,

>«

Рис 5.2

"^<г=0

/+(х)