Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

2.3.

Стабилизация регулятором переменной структуры

121

Применим принцип переменности структуры, положим и = ф{у, у)у и

уа >0,

У<т<0,

0(у,у) =

ll[

где константы fci < О, ^2 > О, с > 0. Тогда в секторе уи > О на фгьзовой

плоскости (у, у) движение системы управления описывается ургшнением (/):

у = fciy, ki < О,

фазовые траектории которого — эллипсы (рис. 2.71а). В секторе

у/т

< О

действует уравнение (//):

у = к2у, к2 > О,

и движение происходит по гиперболическим кривым (рис. 2.716). Видно,

что асимптотическсш устойчивость не наступает ни при положительных,

ни при отрицательных значениях к. Если, однако, фазовые траектории

"сшить" по линиям разрыва (т = О, у = О, то получим асимптотически

устойчивую систему (рис.

2.71

в).

Обозначения / и // на рисунках соответ-

Скользяший

/ режим

Рис.

2.71

ствуют областям действия структур (/) и (//). На прямой (Т = О фазовые

траектории уравнений (7) и (//) направлены "встречно" (рис. 2.72), где f',

f'^ — фазовые скорости. Формгъльно это означает, что

(г&

< О, когда

(Т

/ 0.

о-=0

Рис.

2.72

Следовательно, фазовгш точка не может покинуть прямую разрыва (Т = О,

при дальнейшем движении выполнено равенство и = О и этому движению

отвечает фазовый вектор f" = af' + (1

—

а)/'\ о >0, направленный вдоль

прямой разрыва а = 0.

122 Глава 2. Некоторые принципы

построения

нелинейных регуляторов

Строгий ангииз движения системы в скользящем режиме дает те-

ория А.Ф. Филиппова (определение решения, условия его существо-

вания, единственности, продолжимости вправо и т.д.). Здесь огра-

ничимся эвристическими рассуждениями. Поскольку в скользящем

режиме выполнено равенство

<т

= у + су =

О,

то

I/(t) = i/(ti)e-«(*-*0,

где ti — момент возникновения скользящего режима. Поскольку с >

О, то y{t) -^ О при t —> оо, что и требуется. Значит, задача стаби-

лизации решена. Заметим, что даже если бы имелась информация о

линейной комбинации

<г

= у + су, а не о ее знаке, как выше, то для

получения аналогичного результата с помощью линейной обратной

связи и =

—к<т

потребовалось бы устремление к

—^

оо. Здесь же ко-

эффициенты fci и

Аг2

конечны, что и обеспечивает прочность системе

управления. Таким образом,

• в результате сочетания не являющихся асимптотически устойчи-

выми структур (/ — эллиптической, // — гиперболической) воз-

никло устойчивое движение, которого не было ни у одного из них,

т.е.

появилось новое качество.

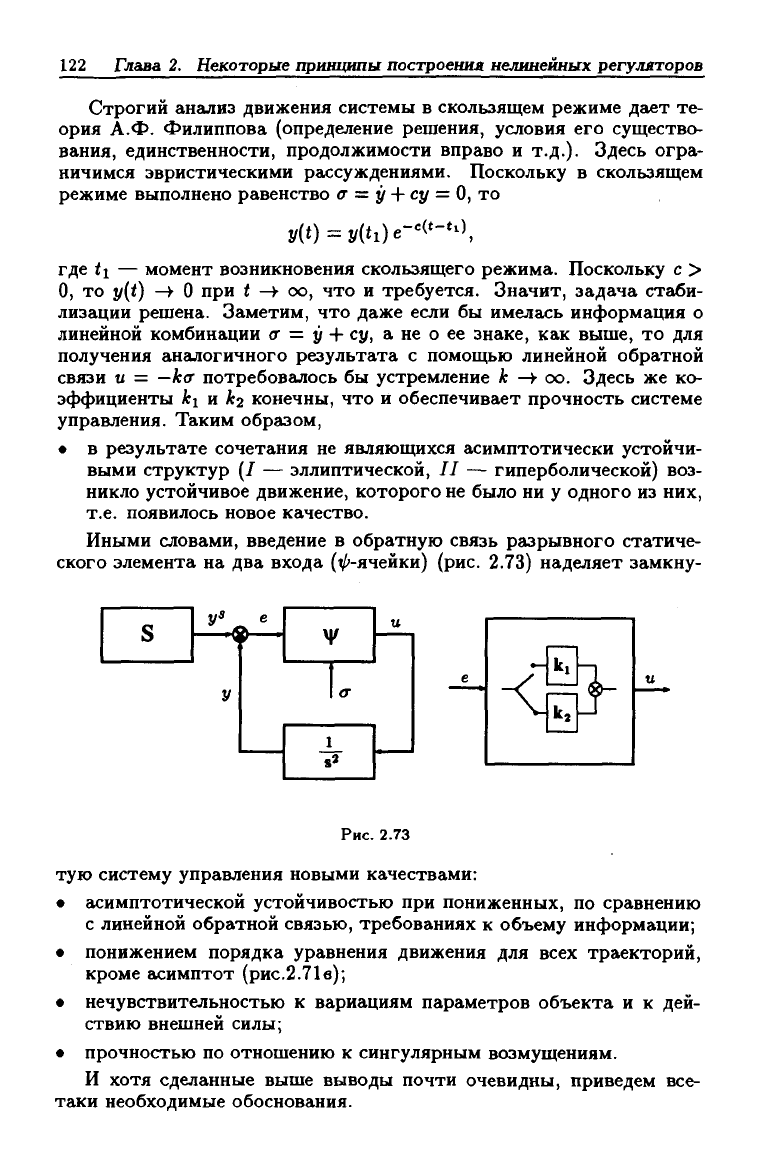
Иными словами, введение в обратную связь разрывного статиче-

ского элемента на два входа (^'-ячейки) (рис. 2.73) наделяет замкну-

i—• \l/ —

Рис. 2.73

<f\^

тую систему управления новыми качествами:

• г1симптотической устойчивостью при пониженных, по сравнению

с линейной обратной связью, требованиях к объему информации;

• понижением порядка уравнения движения для всех траекторий,

кроме асимптот

(рис.2.71

в);

• нечувствительностью к вариациям параметров объекта и к дей-

ствию внешней силы;

• прочностью по отношению к сингулярным возмущениям.

И хотя сделанные выше выводы почти очевидны, приведем все-

таки необходимые обоснования.

2.3.

Стабилизация

регулятором переменной

структуры

123

2.3.6. Анализ прочности СПС по отношению

к параметрическим возмущениям

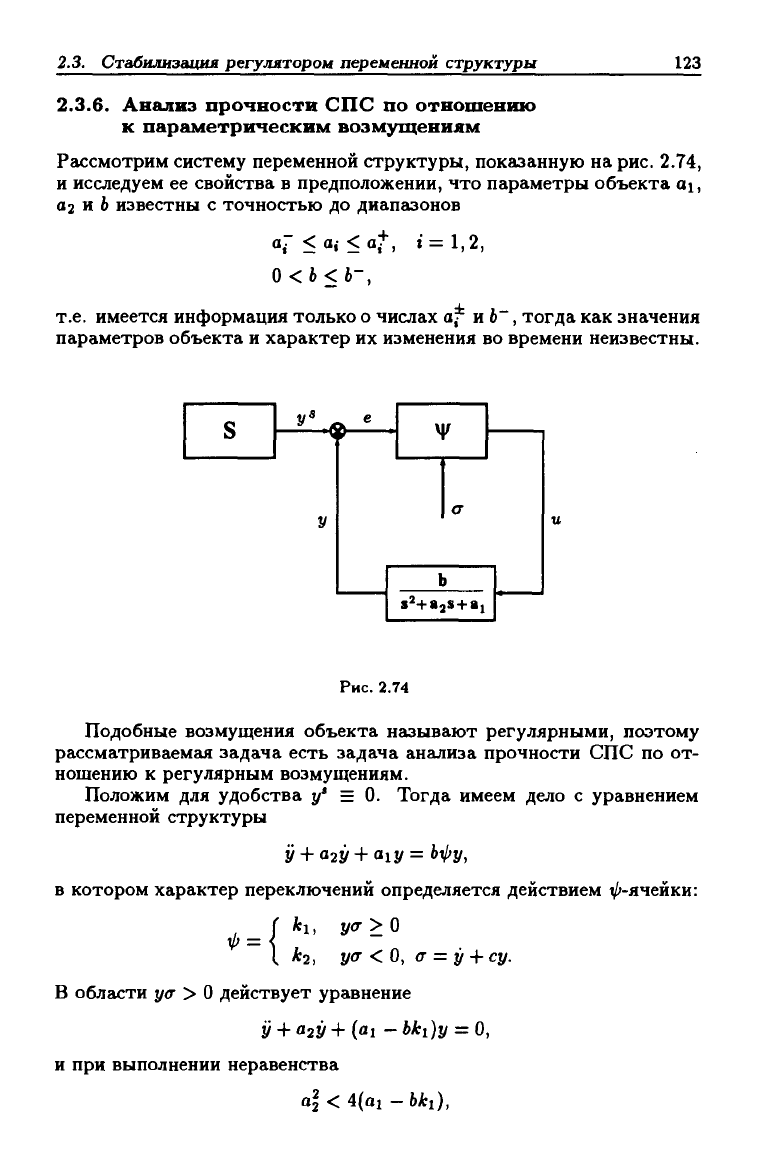
Рассмотрим систему переменной структуры, показанную на рис. 2.74,

и исследуем ее свойства в предположении, что параметры объекта oi,

02 и 6 известны с точностью до диапазонов

о," < «• < «J*"' ^= 1.2.

0<6<Ь-,

т.е.

имеется информация только о числах а* и 6~, тогда как значения

параметров объекта и характер их изменения во времени неизвестны.

1Й

9 * т

i^+ajS+a,

Рис.

2.74

Подобные возмущения объекта называют регулярными, поэтому

рассматриваемая задача есть задача анализа прочности СПС по от-

ношению к регулярным возмущениям.

Положим для удобства у* = 0. Тогда имеем дело с уравнением

переменной структуры

У +

а2У

+ а1у = bipy,

в котором характер переключений определяется действием ^-ячейки:

Г fci, у<т>0

1*2, усг <0,

<г

= у

+ су.

в области j/<T >

действует уравнение

У +

а2У

+ (oi -

f>ki)y

= О,

и при выполнении неравенства

о|<4(о1

-bki),

124 Глава 2. Некоторые принищпы построения нелинейных регуляторов

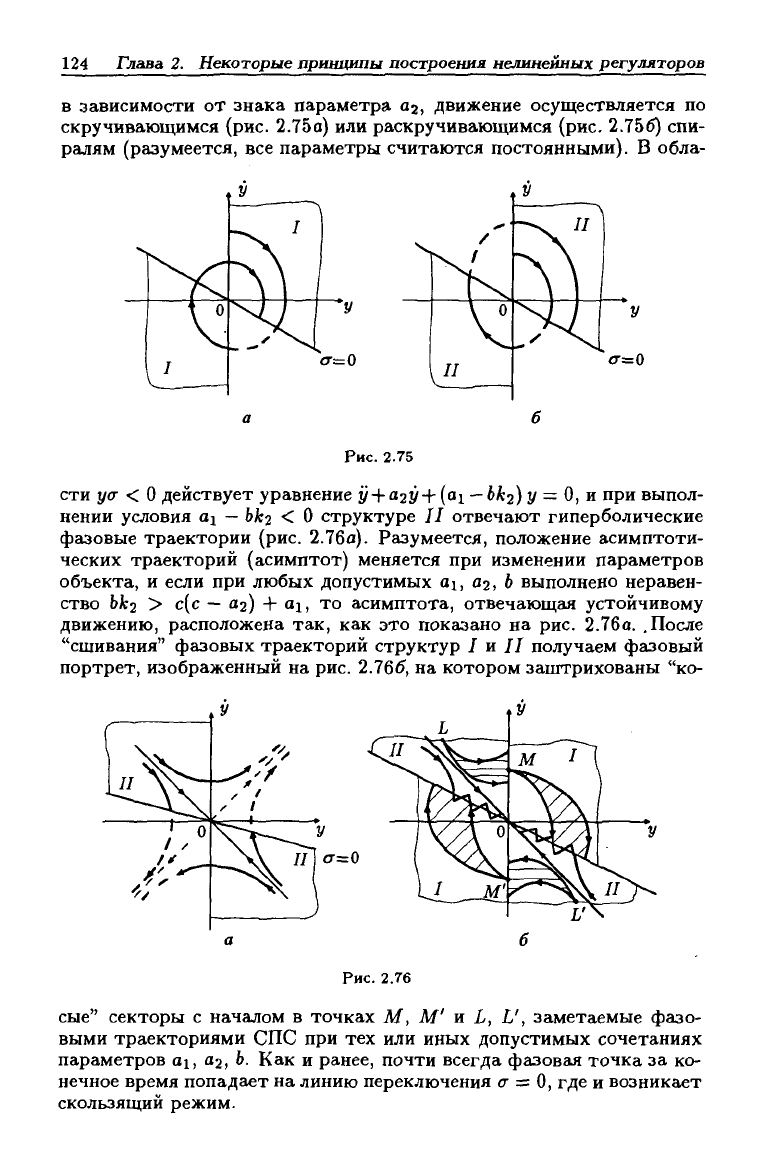
в зависимости от знака параметра аа, движение осуществляется по

скручивающимся (рис. 2.75а) или раскручивающимся (рис. 2.756) спи-

ралям (разумеется, все параметры считаются постоянными). В обла-

<т=0

Рис.

2.75

сти уо- < о действует уравнение y + a2y+{ai —6^2) J/ = О, и при выпол-

нении условия aj

— Ьк2

< О структуре II отвечают гиперболические

фазовые траектории (рис. 2.7ба). Разумеется, положение асимптоти-

ческих траекторий (асимптот) меняется при изменении параметров

объекта, и если при любых допустимых oi, 02, Ь выполнено неравен-

ство 6^2 > с(с

—

ог) + oi, то асимптота, отвечающая устойчивому

движению, расположена так, как это показано на рис. 2.76а. .После

"сшивания" фазовых траекторий структур I и II получаем фазовый

портрет, изображенный на рис. 2.766, на котором заштрихованы "ко-

о-=0

Рис.

2.Г6

сые"

секторы с началом в точках М, М' и L, L', заметаемые фазо-

выми траекториями СПС при тех или иных допустимых сочетаниях

параметров ах, oj, 6. Как и ранее, почти всегда фазовая точка за ко-

нечное время попадает на линию переключения (7 = 0, где и возникает

скользящий режим.

2.3.

Стабилизация регулятором переменной структуры

125

В скользящем режиме движение подчинено уравнению

т.е.

и в этом случае понижается порядок уравнения движения и до-

стигается независимость движения от параметров объекта, при этом

допускается произвольное изменение параметров.

Все сказанное выше справедливо, если имеют место условия

• "попадание" на прямую разрыва

(Г

= О,

• скользящий режим существует на всей прямой а = 0.

Необходимым и достаточным условием попадания является отсут-

ствие вещественных положительных нулей у полинома

ip{s) =

s"^

+ 02 s + (af - 6"iti).

Достаточное условие существования скользящего режима имеет вид

d(T

lim -т-<0,

7->+о at -

da-

lim -r>0

7->-o dt ~

(2.56)

И, так как равенство

={c-

а2)(т

[c(c

- аг)

ai]y + Ьфу,

выполняется при

ki < min

<ч,ь

с{с - аг) - 01

^2 > шах

<ч,ь

с{с - аг) - ai

Заметим, что в условиях стабилизируемости методами СПС от-

сутствуют ограничения на скорость изменения параметров объекта,

тогда как для линейных систем такие ограничения имеются, как, на-

пример, в методе замороженных коэффициентов.

2.3.7. СПС при наличии внехпней силы

Рассмотрим проблему синтеза регулятора переменной структуры для

системы, представленной на рис. 2.77.

s'+a^s+a,

Рис.

2.77

126 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

Уравнения движения системы относительно ошибки и ее производ-

ных имеют вид

e + a2e + aie =-bu + F, (2.57)

где

F = y' + а2у' + aiy' - bf,

и параметры возмущения F находятся в диапазонах

аГ < а, < af, t = 1,2;

< 6" < 6.

Возможны два варианта постановки задачи:

1) функция F{t) известна;

2) функция F{t) не измеряется, но известна ее мажоранта Fm(t), т.е.

при всех t справедлива оценка

\F{t)\

< Fm(t).

Требуется стабилизировать объект (2.57) в нуле с использованием ин-

формации об ошибке е и ее производной ё. Заметим, что традици-

онные средства компенсации F, кроме глубокой обратной связи, для

этой цели не годятся.

При синтезе обратной связи воспользуемся приемом из Примера 17.

Возьмем линию переключения на плоскости (е, ё) в виде

(т

= е + се и

запишем выражение для ее производной в силу уравнений движения

(2.57).

Имеем

&={с-

а2)<г

- [ с(с - аг) +

] е - Ь« + F. (2.58)

Сформируем управление в виде суммы двух компонент и =

+ up,

где первую компоненту Ue выберем, как и ранее, с разрывным коэф-

фициентом, т.е.

{

ki,

е<т

«2.

е<т <

После подстановки этих выражений в (2.58) получим

& = {с-

02)0-

+ buF + F, (2.59)

где

= -[с{с - аз)

-I-

ai]e -|-

ЬфеС.

Бели параметры ^е-ячейки выбраны так, как в Примере 17, а именно:

. c{c-a2) + ai с{с-02)+ ai

ki < mm -i J-'- , «2 > max r-^ ,

ai,b 0 ai,b 0

TO будет выполнено неравенство

(Т&о

< 0. Если теперь вторую компо-

ненту управления up выбрать так, чтобы имело место условие

<т{Ьир

+ F)<0, (2.60)

2.3.

Стабилизация

регулятором переменной

структуры

127

то,

как это видно из выражения

а&= (с

— а2)(т

ff&o

+ a{buF + F),

(2.61)

на поверхности а = О выполняется условие (Т(т < О, и имеет место

скользящий режим. Более того, неравенство (2.60) гарантирует также

и попадание изображающей точки на поверхность а = 0. Действи-

тельно, если при F = О выполнены условия попадания точки на по-

верхность

(Г

= О, то третье слагаемое в (2.61) эти условия усиливает.

Таким образом, если у полиномов

9?='=(s) =s^ + afs + af - b~h

нет положительных вещественных нулей, то условия попадания обес-

печены неравенством (2.60).

Неравенству (2.60) удовлетворяет множество функций up. Укажем

некоторые из них, характерные для СПС. В первом варианте при из-

вестном возмущении F таковой является функция

Up = фр F, фр

<rF>0,

(TF<0,

где b~ li < —I, b~ l2 >l. Bo втором варианте при неизвестном возму-

щении F форма закона сохраняется, но вместо функции F использу-

ется ее мажоранта Fm-

Up = ^pFm, фр

{'"

I h,

ff>0,

ff<0,

где 6- h < -1, b- h > 1.

В структуре синтезированной системы управления д,пя случая из-

меряемого возмущения, изображенной на рис. 2.78, видны две V'-ячей-

ки,

что прямо характеризует эту систему как систему переменной

у'

-^^

Ч-р

"" ffi

|'+•,»+•!

к.

р*

Рис.

2.78

128 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

структуры. В СПС скачкообразно меняется не только коэффициент

обратной связи ^е, но и коэффициент прямой связи по возмущению.

Заметим, что ^-ячейка является функциональным элементом на

два входа, и ее можно представить в виде релейного элемента с изме-

няющейся "полкой" или, иначе, величиной коммутируемого сигнала.

Это хорошо видно при так назывг1емом квазирелейном представлении

^-ячейки.

2.3.8. Квазирелейное представление ^'-ячейки

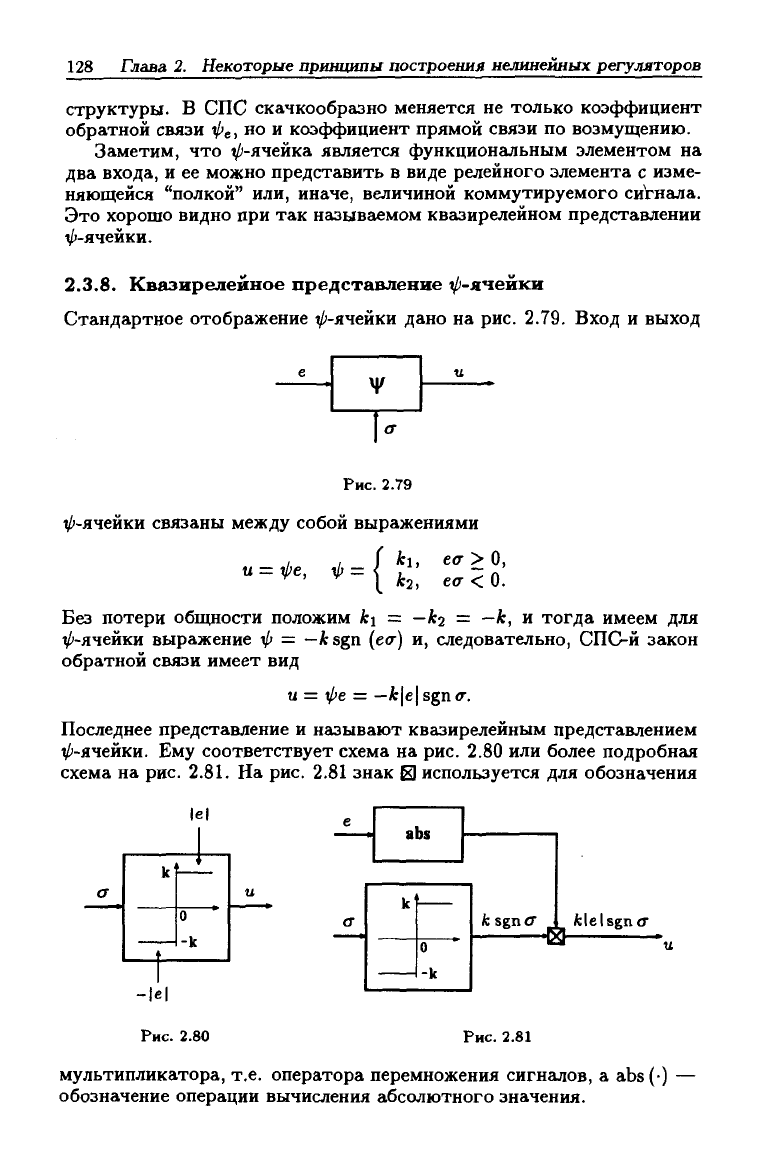
Стандартное отображение ^-ячейки дано на рис. 2.79. Вход и выход

Рис.

2.79

V'-ячейки связаны между собой выражениями

, , ( ki, еа > О,

^ ' ^ \ *2, ео- < 0.

Без потери общности положим hi = —Аз = —к, и тогда имеем для

V'-ячейки выражение V = —Arsgn

{е<т)

и, следовательно, СПС-й закон

обратной связи имеет вид

и = фе =

—к\е\

sgn

ст.

Последнее представление и называют квазирелейным представлением

V'-ячейки. Ему соответствует схема на рис. 2.80 или более подробная

схема на рис. 2.81. На рис. 2.81 знак Н используется для обозначения

|е|

к^^

-|е|

Рис.

2.80

abs

к^

-к

fcsgn<r

{SF

felelsgncr

Рис.

2.81

мультипликатора, т.е. оператора перемножения сигналов, а abs(-)

обозначение операции вычисления абсолютного значения.

2.3.

Стабилизация регулятором переменной структуры

129

Пример 18. СПС при сингулярном возмущении. Исследуем влия-

ние на свойства СПС, синтезированной в Примере 17, временной задержки

в переключениях, т.е. рассмотрим качественное поведение решений следу-

ющего уравнения:

у + а2у + aiy = -bk\y\ sgn^ и,

= у

су, sgn^

<т

= sgn a(t - т),

где все константы и параметры удовлетворяют стандартным условиям, а

т — достаточно малгш постояннгш времени запаздывания. Индекс т озна-

чает, как обычно, что ^'-ячейка "срабатывает" не в момент смены знака

входным сигналом, а через время т. Отсюда следует, что вместо идеаль-

ного скользящего режима, имеющего место при т = О (рис. 2.82

а),

воз-

о-=0

Рис.

2.82

никает режим переключении, называемый реальным скользящим режимом

(рис.

2.826). Если при идеальном скольжении фазовая точка принадлежит

линии а = 0:

(у,

у)

{(у,

у)

|<г

о},

то для достаточно малого г при регишном скольжении фазовая точка нахо-

дится в некоторой окрестности линии

(Т

О,

т.е.

{y,y)&Gr={g(y,y)\W\<5{r)\y\},

где

= 0(т), т.е. S — величина порядка г.

Из рассмотренного примера следует, что асимптотическая устой-

чивость сохраняется при таком сингулярном возмущении, в отличие

от релейной системы (рис. 2.826). Формально сходимость решения к

началу в режиме реального скольжения следует из дифференциаль-

ного уравнения и неравенства, описывающих этот режим:

у + су =

<т,

](г\<6\у\.

Ясно,

что при достаточно мгиюм S (т.е. малом г) имеет место экспо-

ненциальная сходимость к нулю. Иными словами,

• СПС прочна по отношению к сингулярным возмущениям.

130 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

Пример 19. СПС при функциональном возмущении. Рассмо-

трим влияние на качественное поведение СПС функциональной неидеаль-

ности, например, положительного гистерезиса величиной Л > О в пере-

ключениях ^-ячейки. В таком случае имеем дело с уравнением

-I-

02У

-f- oiy = -bk\y\ sgпд

<т,

в котором переключения происходят на поверхности

<г

= у + су,

а все параметры и их выбор описаны в Примере 17.

Свойства рг1зрывного элемента sgnд

тгисовы, что переключение насту-

пает только на линиях

\IT\

= Л после прохождения нуля о- = О, поэтому

вместо стандартного фазового портрета СПС с идегльным скользя1цим ре-

жимом имеем реальный скользящий режим в полосе

\<т\

< Д (рис. 2.83). Это,

Рис.

2.83

конечно, ведет к диссипативности, т.е. к потере свойства асимптотической

устойчивости. Формально этот фгист следует из соотношений

+ су =

(г,

\а\ < Д.

Следовательно,

• СПС не является прочной по отношению к функциональным воз-

мущениям.

2.3.9. Ограничения, недостатки и проблемы теории СПС

Рассмотренные выше примеры и многие другие результаты по теории

и практике систем переменной структуры позволяют сделать выводы,

важные для развития теории обратной связи. Приведем только неко-

торые из них.

• Параметры реального скользящего режима зависят от скрытых

параметров г, Д в рассмотренных выше примерах. Возникающие

при этом "биения", т.е. режимы высокочастотных колебаний в