Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

2.2.

Стабилизация объекта

с неопределенным

оператором

101

При использовании в обратной связи конечных коэффициентов пе-

редачи (именно это является признаком прочной системы) в теории

адаптивного управления регулятор R конструируют в виде двух ком-

понент _

Д = Д + ДД,

где выбор первой компоненты R направляют на стабилизацию опре-

деленного объекта Р, тогда как вторая компонента ДД должна ком-

пенсировать (устранить) влияние неопределенности ДР на поведение

системы.

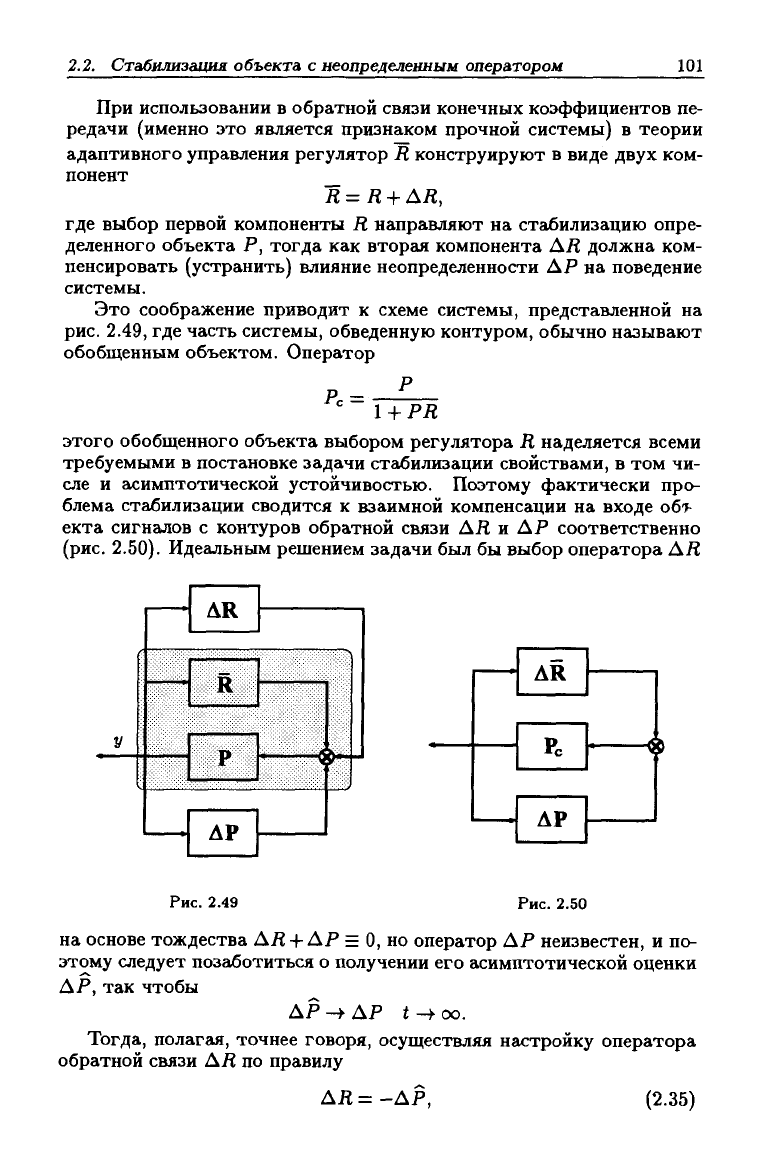
Это соображение приводит к схеме системы, представленной на

рис.

2.49, где часть системы, обведенную контуром, обычно называют

обобщенным объектом. Оператор

^""TTPR

этого обобщенного объекта выбором регулятора Д наделяется всеми

требуемыми в постановке задачи стабилизации свойствами, в том чи-

сле и асимптотической устойчивостью. Поэтому фактически про-

блема стабилизации сводится к взаимной компенсации на входе объ-

екта сигналов с контуров обратной связи ДД и ДР соответственно

(рис.

2.50). Идеальным решением задачи был бы выбор оператора ДД

ДК

АР

>--

АР

Рис.

2.49

Рис.

2.50

на основе тождества AR-\-AP = О, но оператор ДР неизвестен, и по-

этому следует позаботиться о получении его асимптотической оценки

ДР,

так чтобы

ДР ->• ДР t-^oo.

Тогда, полагая, точнее говоря, осуществляя настройку оператора

обратной связи ДД по правилу

ДД=-ДР,

(2.35)

102 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

можно рассчитывать на асимптотическое решение задачи стабилиза-

ции, так как в этом случае справедлива асимптотика

AR + AP = -AP + AP-^0, t-^oo.

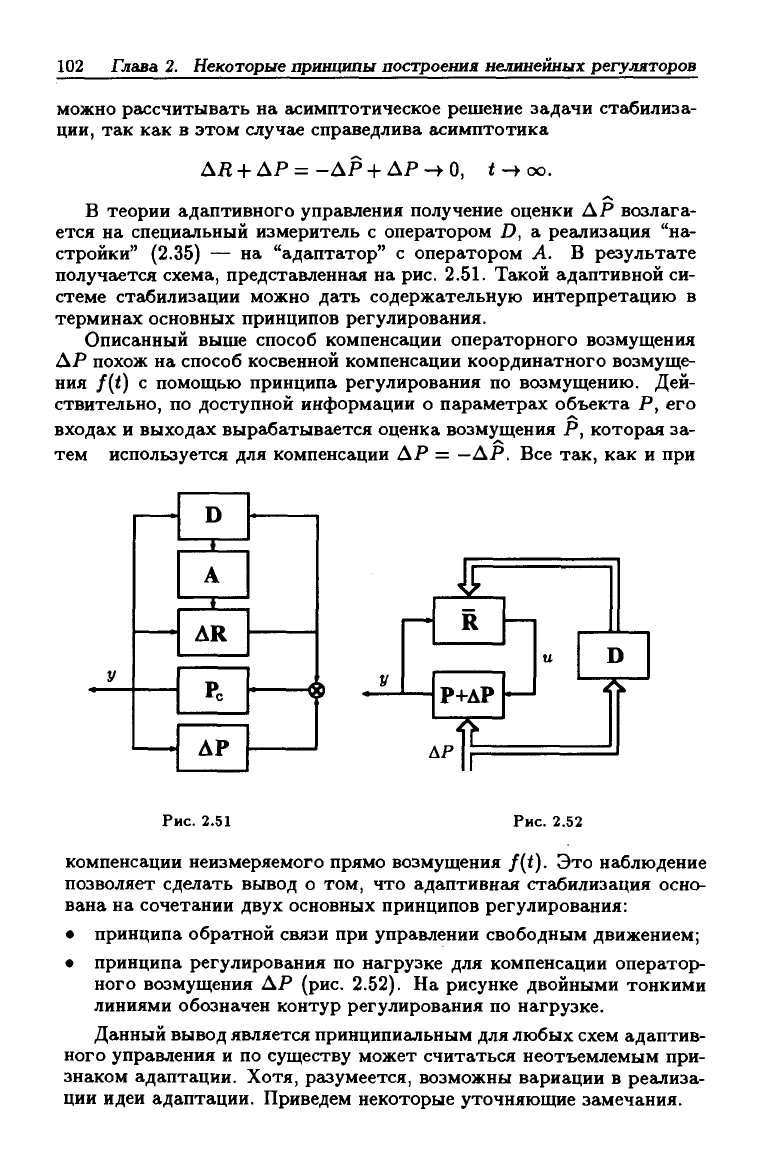
В теории адаптивного управления получение оценки АР возлага-

ется на специальный измеритель с оператором D, а реализация "на-

стройки" (2.35) — на "адаптатор" с оператором А. В результате

получается схема, представленная на рис. 2.51. Такой адаптивной си-

стеме стабилизации можно дать содержательную интерпретацию в

терминах основных принципов регулирования.

Описанный выше способ компенсации операторного возмущения

АР похож на способ косвенной компенсации координатного возмуще-

ния /(f) с помощью принципа регулирования по возмущению. Дей-

ствительно, по доступной информации о параметрах объекта Р, его

входах и выходах вырабатывается оценка возмущения Р, которая за-

тем используется для компенсации АР = —АР. Все так, как и при

АР

-9

Р+АР

-f

Рис. 2.51

Рис. 2.52

компенсации неизмеряемого прямо возмущения /(<). Это наблюдение

позволяет сделать вывод о том, что адаптивная стабилизация осно-

вана на сочетании двух основных принципов регулирования:

• принципа обратной связи при управлении свободным движением;

• принципа регулирования по нагрузке для компенсации оператор-

ного возмущения АР (рис. 2.52). На рисунке двойными тонкими

линиями обозначен контур регулирования по нагрузке.

Данный вывод является принципиальным для любых схем адаптив-

ного управления и по существу может считаться неотъемлемым при-

знаком адаптации. Хотя, разумеется, возможны вариации в реализа-

ции идеи адаптации. Приведем некоторые уточняющие замечания.

2.2.

Стабилизация объекта с неопределенным оператором

103

Замечание 1. Имеются варигщии описанной выше схемы адаптгщии.

Например, для выполнения условия компенсации

ДЛ+ДР=0

можно менять не только (а может быть и не столько) оператор регулятора

AR,

но и оператор объекта ДР. Для этого, разумеется, должна иметься

соответствующая возможность представления ДР в виде суммы

ДР = ДР' + ДР",

где ДР' — неизвестная, а ДР" — настраиваемг1Я часть. В этом случгке го-

ворят о методе нгкстраивг1емого объекта, в отличие от предыдущего случая,

когда мы имели дело с настргкиваемой обратной связью.

Замечание 2. Поскольку оценка ДР вырабатывается по измерениям

координат объекта р или системы Рс, а также их входов, то понятно, что

наиболее просто это делается тогда, когда изменения ДР происходят "мед-

леннее" изменений этих переменных. В этом смысле говорят о квазиста-

ционарном изменении оператора ДР, а фгжтически при расчете обратной

связи ориентируются на стационарный оператор ДР. Бели построенная та-

ким образом адгиггивная система прочна, то она сохраняет работоспособ-

ность и при "медленных" изменениях в силу устойчивости прочных систем

по отношению к постоянно действующим возмущениям.

Замечание 3. Нг1личие внешнего воздействия / на неопределенный

объект упргшления (рис. 2.53) еще более усложняет ситуацию, так как при

этом вносится дополнительн£1Я неустранимая погрешность в оценку Др,

если только Д/ -/^ О при t

—¥

оо. Поэтому вместо требуемого условием

компенсгщии ргшенства

ДД+ДР=0

имеем смещенное на некоторую величину Д^ рг1венство

ДД + ДР = Д(г,

и проблема, следовательно, состоит только в том, насколько оператор Д^

искажает поведение объекта Рс (рис. 2.54). Если возмущение исчезающее.

Р+АР

Рс

Рис.

2.53

Рис.

2.54

т.е.

—>

О, а вместе с этим и ДQ

—>

О при t —^ оо, то в установившемся

режиме проблемы не возникг1ет. Если же возмущение не исчезающее, т.е.

Д/ 7^

при t -)• оо, но, нгшример, огргшиченное, т.е. (/| < /о = const, то

104 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

из-за использования ограниченных коэффициентов передачи в регуляторе

можно рассчитывать, вообще говоря, только на диссипативность замкнутой

системы упргюления с радиусом диссипативности порядка /о.

Замечание 4. При определенных условиях адаптивный подход поро-

ждает стабилизаторы универсального действия, т.е. тгисие регуляторы, для

применения которых нет необходимости точно знать не только параметры

объекта, но даже и его порядок. Подобные регуляторы называются уни-

версальными. Для успешного их использования требуется выполнение сле-

дующих условий:

• МС-условия (условия согласованности);

• минимальной фазовости объекта Р.

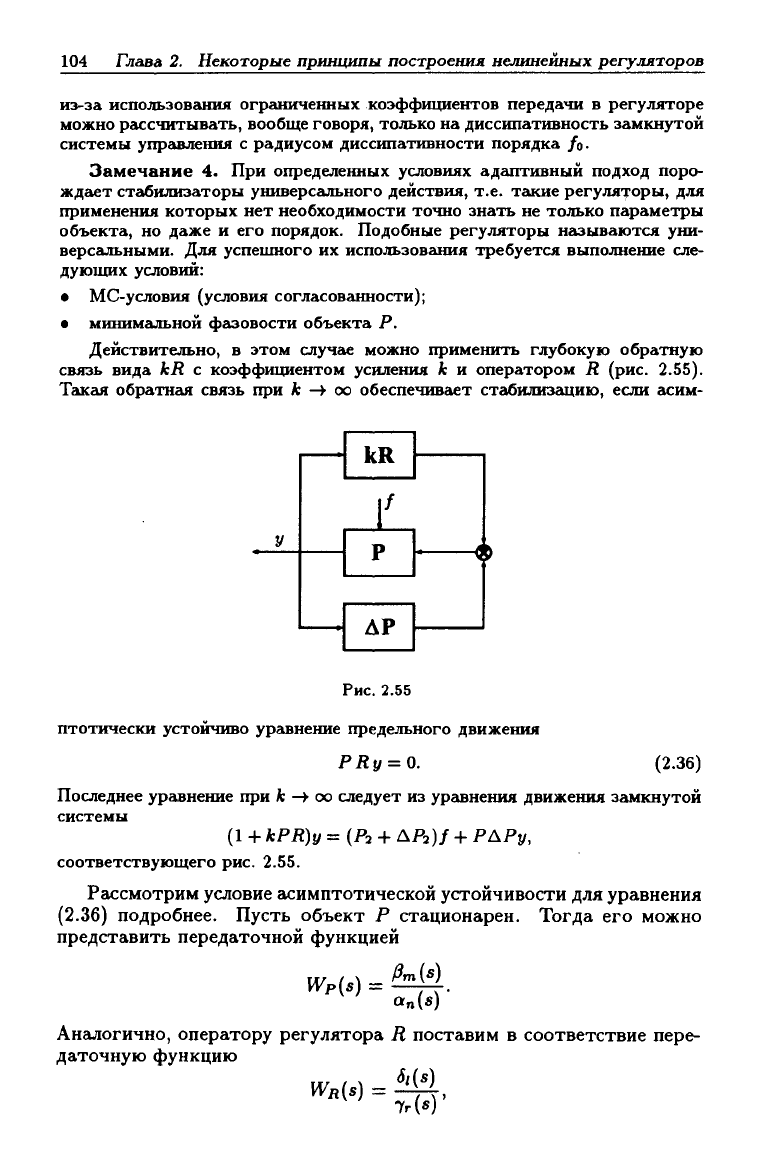
Действительно, в этом случае можно применить глубокую обратную

связь вида kR с коэффищ1ентом усиления к и оператором R (рис. 2.55).

Такая обратнёкя связь при к -^ оо обеспечивгъет стгъбилизгщию, если асим-

АР

• f S

Рис. 2.55

птотически устойчиво уравнение предельного движения

РЯу = 0.

(2.36)

Последнее уравнение при

А;

^ оо следует из уравнения движения замкнутой

системы

-I-

kPR)y = (Рг + ДРг)/ + РАРу,

соответствующего рис. 2.55.

Рассмотрим условие асимптотической устойчивости для уравнения

(2.36) подробнее. Пусть объект Р стационарен. Тогда его можно

представить передаточной функцией

Wp{s)

I3m(s)

an{s) '

Аналогично, оператору регулятора R поставим в соответствие пере-

даточную функцию

2.2.

Стабилизация объекта

с неопределенный

оператором

105

где /3, а, S, f — полиномы комплексной переменной s, а индексы т,

п,

I я г — степени соответствующих полиномов. Тогда уравнение

предельного движения

PRy =

эквивалентно уравнению

p,r^{s)Si{s)Y(s)

= 0, (2.37)

где Y{s) = С[у] — одностороннее преобразование Лапласа функции

y{t).

Из (2.37) видно, что полином /?m(s) должен быть гурвицевым,

что и означает минимальную фазовость объекта Р.

Непрочность рассматриваемой системы с глубокой обратной свя-

зью в универсальном стабилизаторе преодолевается тем, что коэффи-

циент обратной связи зависит от переменных состояния, например,

от выхода объекта

к{у,...),

и монотонно увеличивается до тех пор, пока не наступает, при указан-

ных выше условиях, устойчивость (при /

—>

0) или диссипативность

(при 1/1 < /о) следующего уравнения:

(.Щ^'")

+ PRjy = {P2 + ДРз)/ + РАРу.

Пример 13. Синтез адаптивной системы управления. Рассмо-

трим на примере стабилизации в нуле объекта второго порядка

Х2 = axi +bu, \ • I

с неопределенными коэффициентами а и Ь > О, одну из наиболее распро-

страненных методик синтеза адаптивного управления.

Замкнем объект (2.38) обратной связью

U = —fclXl — ^2^2

и сформируем алгоритмы адглтации Л переменных ^i, ^2:

*:i=6,

^2=6, (2.39)

т.е.

г1лгоритмы настройки параметров ki, /сг, таким образом, чтобы пове-

дение замкнутой системы Е*:

XI = Х2,

Х2

—{bki —

a)xi

—

bfcjxa,

было бы подобно (может быть, даже близко) поведению некоторой эталон-

ной системы Е-,:

«1 = 22,

22 = -7121 - 7222.

106 Глава 2. Некоторые принципы построения нелинейных регуляторов

Здесь 71 и

— назначенные положительные числа; Е.у-систему будем также

называть моделью. После введения обозначений

bAfci = bki

—

711 ЬАк2 = bfcj

—

замкнутую адаптируемой обратной связью Е;ь-систему можно представить

в стандартном виде

XI = 12,

Х2 = —71^1

—

721^2

—

b/\kixi

—

ЬАк2Х2.

в условиях гипотезы квазистационарности Aki = ki, А^г = ^2, и по-

этому формально удобно считать, что адаптируются не сами коэффици-

енты ki и ^2, а их отклонения от требуемых значений, т.е. згккон адаптации

А можно згшисать в обобщенном виде Aki =

^1,

ДЛг = ^2-

Для получения конкретного алгоритма адгштации Л используем квадра-

тичную форму t)(x) = (х, Нх) с положительно определенной (2 х 2)-матрицей

Н = [hi,h2]'*', тгисую, что при некотором (желаемом) положительном числе

Л > О, определяющем степень устойчивости Е-^-системы (модели поведения

замкнутой системы), ее производная в силу Е-^-системы имеет вид

I) 1

= -2Xv.

Is.,

Поскольку выбор параметров модели 7i, 72 ничем не огргшичен, такие мат-

рица Н и число А существуют.

Введем теперь в рассмотрение квадратичную форму V{x,k) в расши-

ренном простргшстве переменных {х, к} выражением

,^, ,, , , bfAkj Akl\

Vix,k) =

vix)+-i^-^+^j,

где Pi,

132

— некоторые положительные числа. Ее производная в силу Е*-

системы с алгоритмом адглтации Л дается выражением

^U =^U-(^-.( г )>(А^1-1 +А.2Х2)-ЬЬ (^ + ^) =

= -2\{х,Нх) -Ь Aki(xia-^\-\-Ak2(x2(T-^\ , (2.

где "• = ( Нх, ( 1 ) ) = {^2,х). Теперь ясно, что если правые части алго-

ритма адаптации выбрать в виде

$1 = /?lXl<T, ^2 = /32Х2<Т,

то производнскя (2.40) принимает вид

V = -2Х{х, Нх)

и становится знгикоотрицательной в простргшстве {х, к}, откуда и следует

стабилизируемость рассматриваемой системы.

40)

2.3.

Стабилиза1щя регулятором переменной структуры

107

Заметим, что сходимость погрешностей оценок Afci, Д^г к нулю при

этом не гарантируется, поскольку для такой сходимости требуется опре-

деленная отрицательность v в расширенном фазовом пространстве {х, к}.

Заметим также, мто при нгшичии координатного- возмущения /, т.е. при

стабилизации объекта Р' :

XI = Х2,

Х2 = —ахх -\-Ьи + f

указгшным выше способом, в итоговом выражении для производной v по-

явится дополнительное слагёкемое, пропорционгшьное возмущению

v = -2\{xi,Hx) + b(Tf,

которое при неизвестном / нарушает знакоотрицательность v и Хфи ограни-

чении 1/1 < /о ведет к диссипативности системы по основным переменным,

т.е.

задача стабилизации не решс1ется точно.

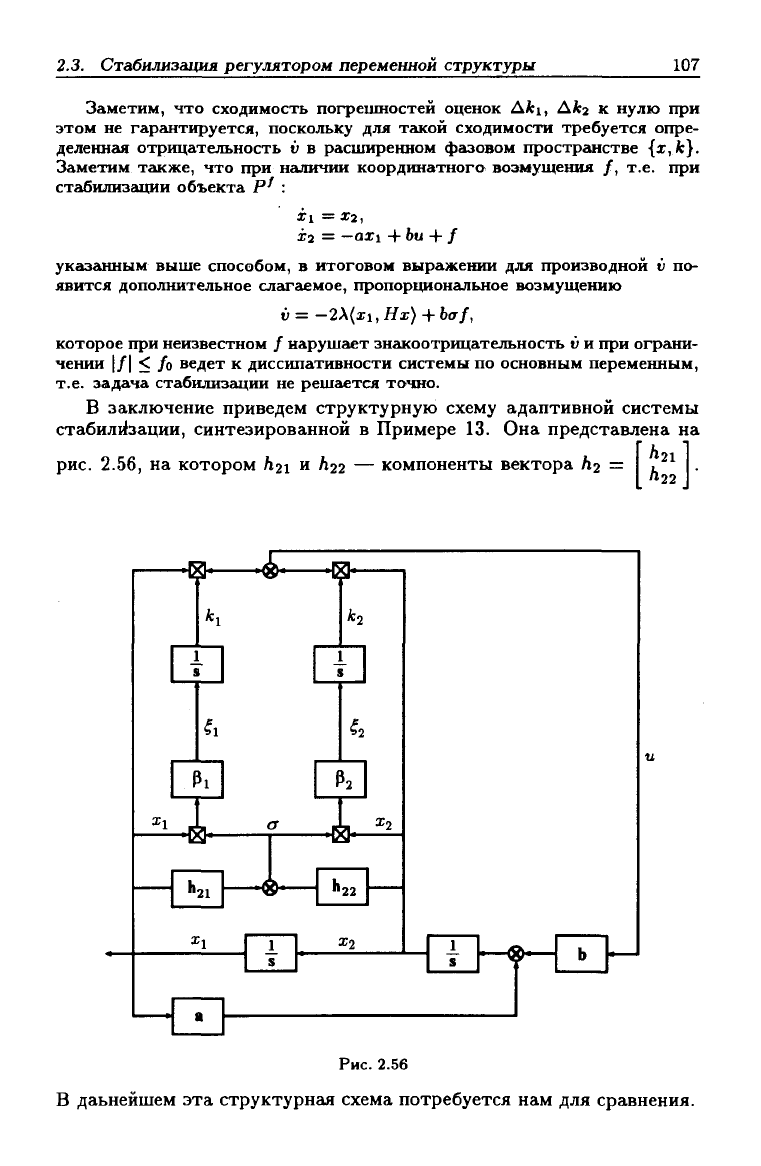
В заключение приведем структурную схему адаптивной системы

стабилизации, синтезированной в Примере 13. Она представлена на

рис.

2.56, на котором /i2i и Лгг — компоненты вектора Лг = i^^

"22

Рис.

2.56

В даьнейшем эта структурнг1я схема потребуется нам для сравнения.

108 Глава 2. Некоторые принципы построения нелинейных регуляторов

2.3.

Стабилизация регулятором

переменной структуры

Рассмотрим теперь еще одну попытку окончательного решения рас-

сматриваемой в монографии проблемы путем использования регуля-

торов с переменной структурой.

Идея принципа переменности структуры состоит в скачкообрг13-

ном изменении связей между функционгшьными элементами регуля-

тора в зависимости от фазового состояния замкнутой системы упра-

вления, которую в таком случае называют системой управления пе-

ременной структуры (СПС). Если рассматриваются линейные объект

и функциональные элементы регулятора, то соответствующую СПС

можно интерпретировать как совокупность линейных подсистем и

правил перехода от одного элемента этой совокупности к другому при

пересечении фазовой точкой разделительных гиперплоскостей в фа-

зовом пространстве системы, которые называют поверхностями ргиз-

рыва. Если же объект или функциональные элементы нелинейны, то

речь идет о совокупности нелинейных подсистем и, соответственно, о

нелинейных поверхностях или многообразиях разрыва.

И в первом и во втором случае СПС — нелинейная динамическая

система — описывается дифференциальными уравнениями с разрыв-

ными правыми частями. Синтез СПС сводится к выбору поверхно-

стей разрыва и исходной совокупности подсистем, гарантирующих

решение поставленной задачи управления. Мы не излагаем здесь те-

орию СПС, просто хотим подчеркнуть, что СПС предназначены для

робастного управления объектом со структурированной неопределен-

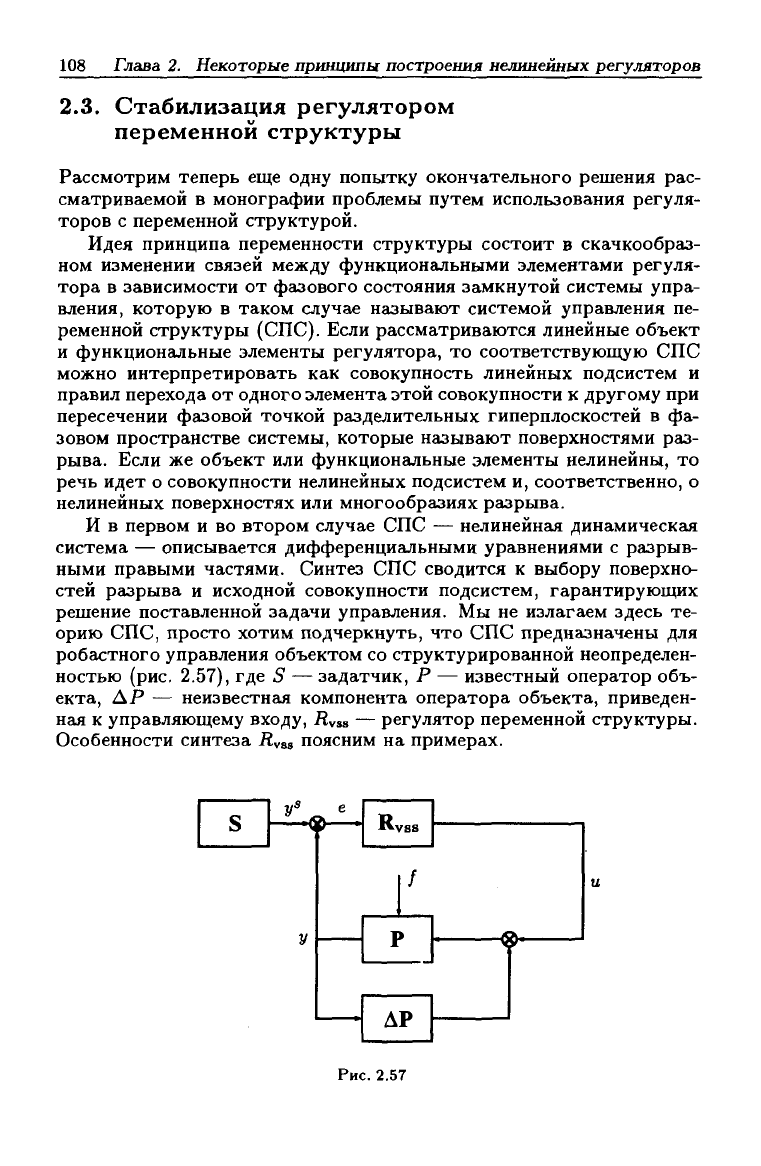
ностью (рис. 2.57), где S — задатчик, Р — известный оператор объ-

екта, АР — неизвестная компонента оператора объекта, приведен-

ная к управляющему входу, Rvss — регулятор переменной структуры.

Особенности синтеза Rvss поясним на примерах.

Н2>-

АР

н»-

Рис.

2.57

2.3.

Стабилизация

регулятором переменной

структуры

109

2.3.1.

Астатическая следящая система

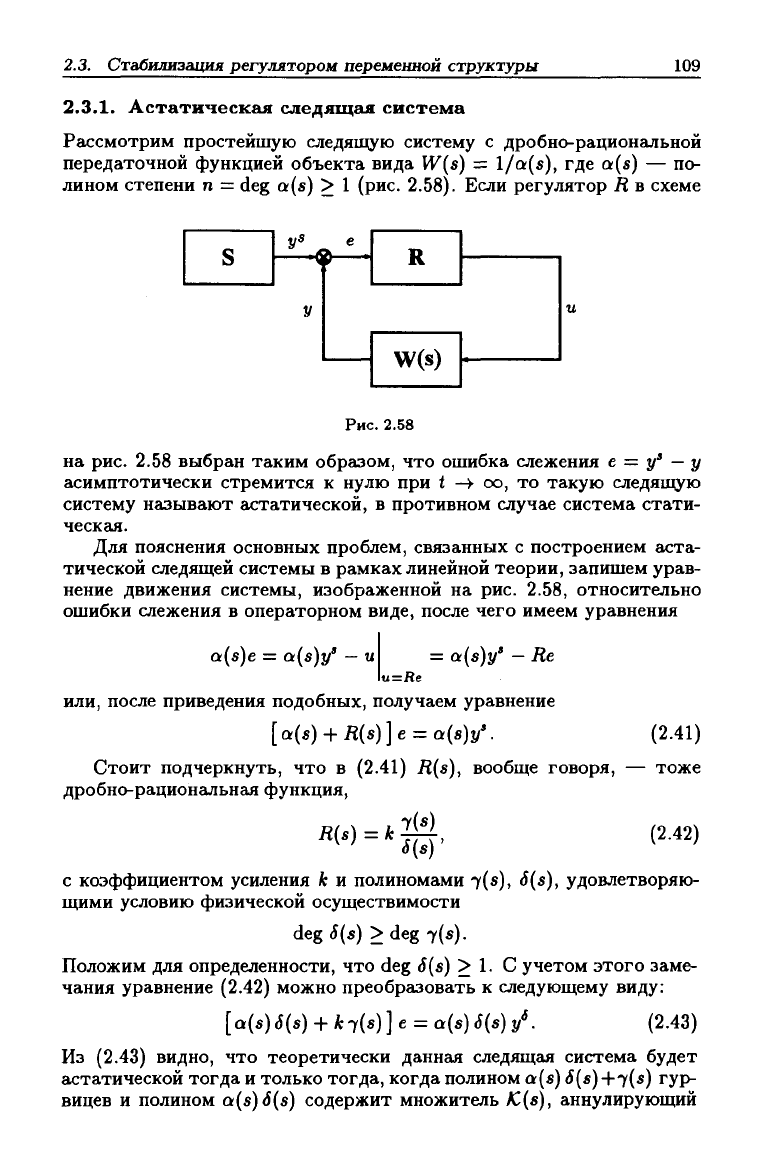
Рассмотрим простейшую следящую систему с дробно-рациональной

передаточной функцией объекта вида W(s) — l/a(s), где a(s) — по-

лином степени п = deg a(s) > 1 (рис. 2.58). Если регулятор R в схеме

-9

W(s)

Рис. 2.58

на рис. 2.58 выбран таким образом, что ошибка слежения е = у'

—

асимптотически стремится к нулю при <

—>•

оо, то такую следящую

систему называют астатической, в противном случае система стати-

ческая.

Для пояснения основных проблем, связанных с построением аста-

тической следящей системы в рамках линейной теории, запишем урав-

нение движения системы, изображенной на рис. 2.58, относительно

ошибки слежения в операторном виде, после чего имеем уравнения

a(s)e = a(s)y'

—

и = a(s)y' - Re

u=Re

или, после приведения подобных, получаем уравнение

[a{s) + R{s)]e = a{8)y'. (2.41)

Стоит подчеркнуть, что в (2.41) R{s), вообще говоря, — тоже

дробно-рациональная функция,

lis)

R{s) = к

4s)'

(2.42)

с коэффициентом усиления к и полиномами 7(*)> '^(*)i удовлетворяю-

щими условию физической осуществимости

deg S{s) > deg 7(*)-

Положим для определенности, что deg S(s) > 1. С учетом этого заме-

чания уравнение (2.42) можно преобразовать к следующему виду:

(2.43)

Из (2.43) видно, что теоретически данная следящг1я система будет

астатической тогда и только тогда, когда полином a(s) S{s)+'f(s) гур-

вицев и полином a(s)<J(s) содержит множитель /C(s), аннулирующий

[ a{s) 6{s) +

7(s)

]

е = a{s) S{s) /.

110 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

функцию задания, т.е. такой, что

K{s)y' = О, (2.44)

либо,

если такого множителя K{s) нет, то:

1) полином 7(e) должен быть гурвицев;

2) в пределе при к

—¥

оо поведение системы описывается асимптоти-

чески устойчивым уравнением

l{s)e = 0. (2.45)

Впрочем, так как большие коэффициенты усиления приводят к не-

грубым системам, то реально при синтезе астатических систем при-

ходится ориентироваться на конечные коэффициенты передачи, а зна-

чит, и на гурвицевость полинома a{s) 5{s) + 7(5) и условие (2.44).

Если аннулирующий полином

IC{s)

является гурвицевым, то выпол-

нение указанных выше условий не вызывает принципигшьных ослож-

нений. Другое дело, когда полином /C(s) — неустойчивый, например

/С(в) = s^

—

а^, о = const > 0. Тогда мы сталкиваемся с серьезными

проблемами. В самом деле, полином S{s) не может быть неустойчи-

вым, ибо в противном случае неустойчива собственная динамика ре-

гулятора (2.42) и его выход u{t) экспоненциально нарастает со всеми

вытекаюпщми отсюда негативными последствиями: выходом за пре-

делы зоны линейности и т.п. Следовательно, неустойчивые компо-

ненты (множители) аннулирующего оператора K{s) должны быть од-

новременно множителями полинома a(s), что, конечно, неве{)оятно.

Это рассуждение показывает, что

• в рамках линейной теории управления, предполагающей исполь-

зование только ограниченных коэффициентов передачи в регуля-

торе,

построить гютатическую систему слежения за экспоненци-

ально растущим сигналом у' невозможно.

Мы рассмотрели две грубые ситуации: экспоненциально устойчи-

вые и экспоненциально неустойчивые K{s). Проанализируем теперь

пограничную ситуацию, когда задание

j/'

— полиномиально рги;тущая

функция времени, т.е.

у' = Cm+l^ +

С^*'"-Ч

... +С1,

где с,- — некоторые константы, (t = 1, ...

-(-

1), а число m — по-

рядок полинома, т.е. Cm+i ф 0. Простейшим оператором, аннулиру-

ющим полином (2.45), очевидно, является оператор (т -I- 1)-кратного

дифференцирования K{s) =

s"*'^^.

Естественно предполагать, что в

систему слежения он привносится регулятором, т.е.

S{8) = 5-+1

S'{S),

где S'(s) — некоторый устойчивый полином. Но в таком случае, в силу

необходимого условия устойчивости, для обеспечения гурвицевости