Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

2.1.

Релейная

обратная

связь

2.1.2.

Скользящий режим в точке

В релейных системах часто возникает скользящий режим. Для пояс-

нения приведем следующий пример:

ё + ае = —sgn е, а = const.

Фс13овое пространство системы (2.4) одномерно (рис. 2.6).

(2.4)

\а\

Рис.

2.6

Из (2.4) нетрудно понять, что неустойчивый объект (т.е. когда

а < 0) стабилизируется в нуле для любых начальных условий е(0) из

интервала

(—1/|а|,

1/|а|),

тогда как устойчивый объект (т.е. а > 0)

стабилизируется в нуле на всей прямой для любых начальных условий

(—оо,оо). В окрестности точки

фазовые траектории системы (2.4)

направлены навстречу друг другу и, следовательно, фазовая точка

не может покинуть точку 0. Решение е = О не является "классиче-

ским" и должно пониматься в каком-то ином смысле, например по

А.Ф.Филиппову [72]. Такому решению отвечают бесконечно частые

переключения релейного элемента. Эти переключения ассоциируются

со скользящим режимом.

Исследуем скользящий режим в системе (2.4) более подробно. Для

этого представим ее геометрически в виде многообразия на плоско-

сти (е,ё) (рис. 2.7). Слева от нуля движение происходит по прямой

ё-\- ае = 1, а справа — по прямой ё -f- ае = —1. Отрезок [1,-1]

на оси е = О есть отрезок скользящего режима, когда скачком ме-

няется уравнение движения. Выясним, что произойдет с системой

при появлении задержки в переключениях РЭ. Задержка в переключе-

нии может быть пространственной или временной. В первом случае

(рис.

2.8а) релейный элемент имеет петлю гистерезиса шириной 2Д и

для него используем обозначение sgnд е, а во втором случае (рис. 2.86)

переключение происходит через время г после смены знака входным

сигналом. Соответствующий элемент обозначен через sgn^ е = sgner,

где

— постоянная времени запаздывания.

-1

Ри

с. 2.7

-Д

-1

бг

Рис.

2.8

е-"

72 Паава 2.

Некоторые

принципы

построения

нелинейных регуляторов

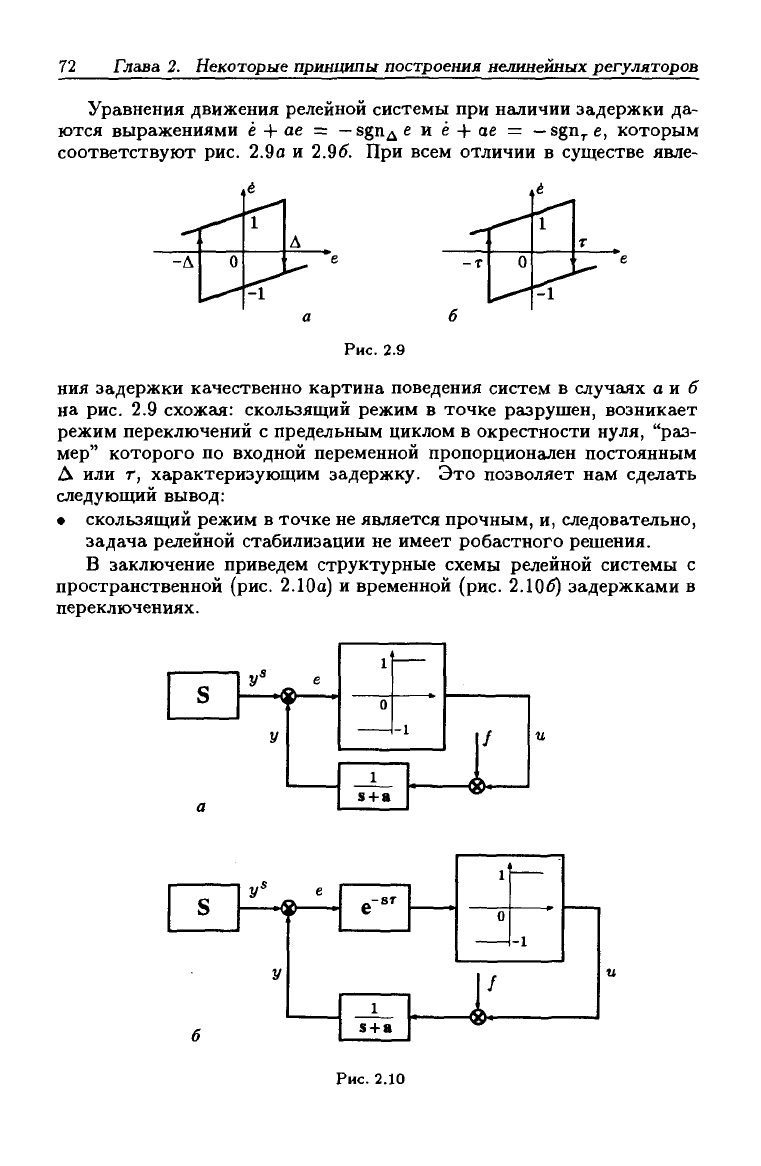
Уравнения движения релейной системы при наличии задержки да-

ются выражениями ё + ае =

—

8§пд е и ё + ае =

—

sgn^ е, которым

соответствуют рис. 2.9а и 2.9^. При всем отличии в существе явле-

-т

"-С

Рис. 2.9

ния задержки качественно картина поведения систем в случаях а и 5

на рис. 2.9 схожая: скользящий режим в точке разрушен, возникает

режим переключений с предельным циклом в окрестности нуля, "раз-

мер"

которого по входной переменной пропорционален постоянным

Д или г, характеризующим задержку. Это позволяет нам сделать

следующий вывод:

• скользящий режим в точке не является прочным, и, следовательно,

задача релейной стабилизации не имеет робастного решения.

В заключение приведем структурные схемы релейной системы с

пространственной (рис. 2.10а) и временной (рис. 2.106) задержками в

переключениях.

Ф-

s + a

Л . е

s + a

Рис. 2.10

2.1.

Релейная обратная связь

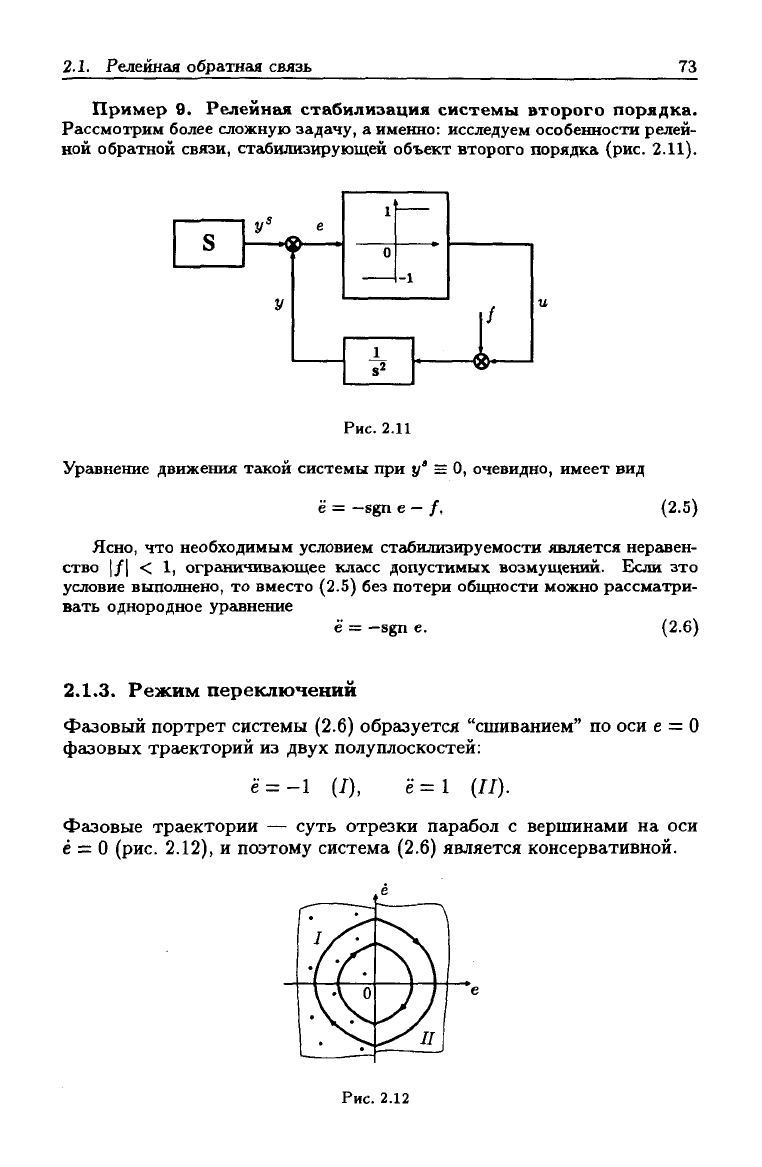
Пример 9. Релейная стабилизация системы второго порядка.

Рассмотрим более сложную задачу, а именно: исследуем особенности релей-

ной обратной связи, стг1билизирующей объект второго порядка (рис. 2.11).

У^ е

-1

«2

. JL

Рис. 2.11

Ургшнение движения такой системы при у' = О, очевидно, имеет вид

ё = —sgn е

—

/, (2.5)

Ясно,

что необходимым условием стабилизируемости является нергшен-

ство 1/1 < 1, ограничивающее класс допустимых возмущений. Если это

условие выполнено, то вместо (2.5) без потери общности можно рассматри-

вать однородное уравнение

ё = —sgn е. (2.6)

2.1.3.

Режим переключений

Фазовый портрет системы (2.6) образуется "сшиванием" по оси е = О

фазовых трг1екторий из двух полуплоскостей:

ё = -1 (/), ё = 1 {II).

Фазовые траектории — суть отрезки парабол с вершинами на оси

6 = 0 (рис. 2.12), и поэтому система (2.6) является консервативной.

Рис. 2.12

74 Глава 2.

Некоторые

пршщипы

построения

нелинейных регуляторов

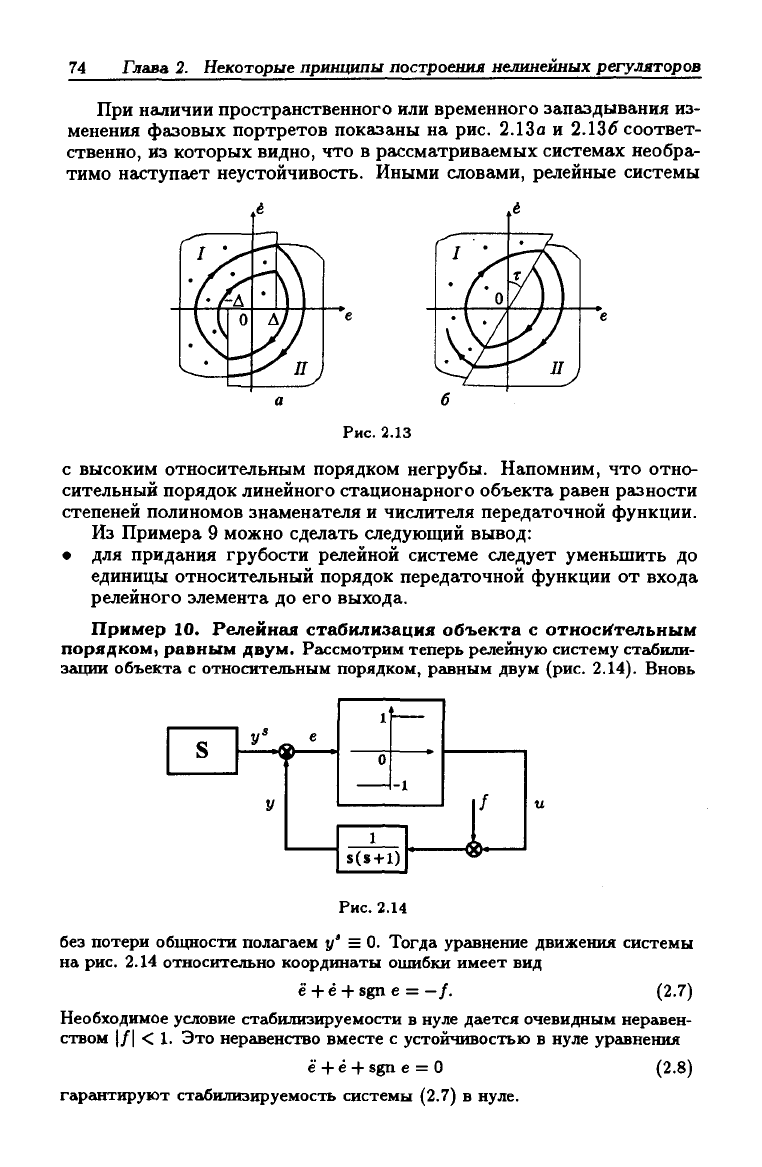
При наличии пространственного или временного запаздывания из-

менения фазовых портретов показаны на рис. 2.13а и 2.13^ соответ-

ственно, из которых видно, что в рассматриваемых системах необра-

тимо наступает неустойчивость. Иными словами, релейные системы

/ "^

• л V'

I'fb.

•

Ч }

'Уп)

Рис.

2.13

С ВЫСОКИМ относительным порядком негрубы. Напомним, что отно-

сительный порядок линейного стационарного объекта равен разности

степеней полиномов знаменателя и числителя передаточной функции.

Из Примера 9 можно сделать следующий вывод:

• для придания грубости релейной системе следует уменьшить до

единицы относительный порядок передаточной функции от входа

релейного элемента до его выхода.

Пример 10. Релейная стабилизация объекта с относительным

порядком, равным двум. Рассмотрим теперь релейную систему стабили-

зации объекта с относительным порядком, равным двум (рис. 2.14). Вновь

S -^

J—

s(s + ]

-1

) —

Рис.

2.14

без потери общности полгъгаем

j/'

= 0. Тогда уравнение движения системы

на рис. 2.14 относительно координаты ошибки имеет вид

-I-

sgn е = -/. (2.7)

Необходимое условие стабилизируемости в нуле дается очевидным неравен-

ством 1/1 < 1. Это неравенство вместе с устойчивостью в нуле уравнения

-I-

sgn е =

(2.8)

гаргштируют стг1билизируемость системы (2.7) в нуле.

2.1.

Релейная обратная связь 75

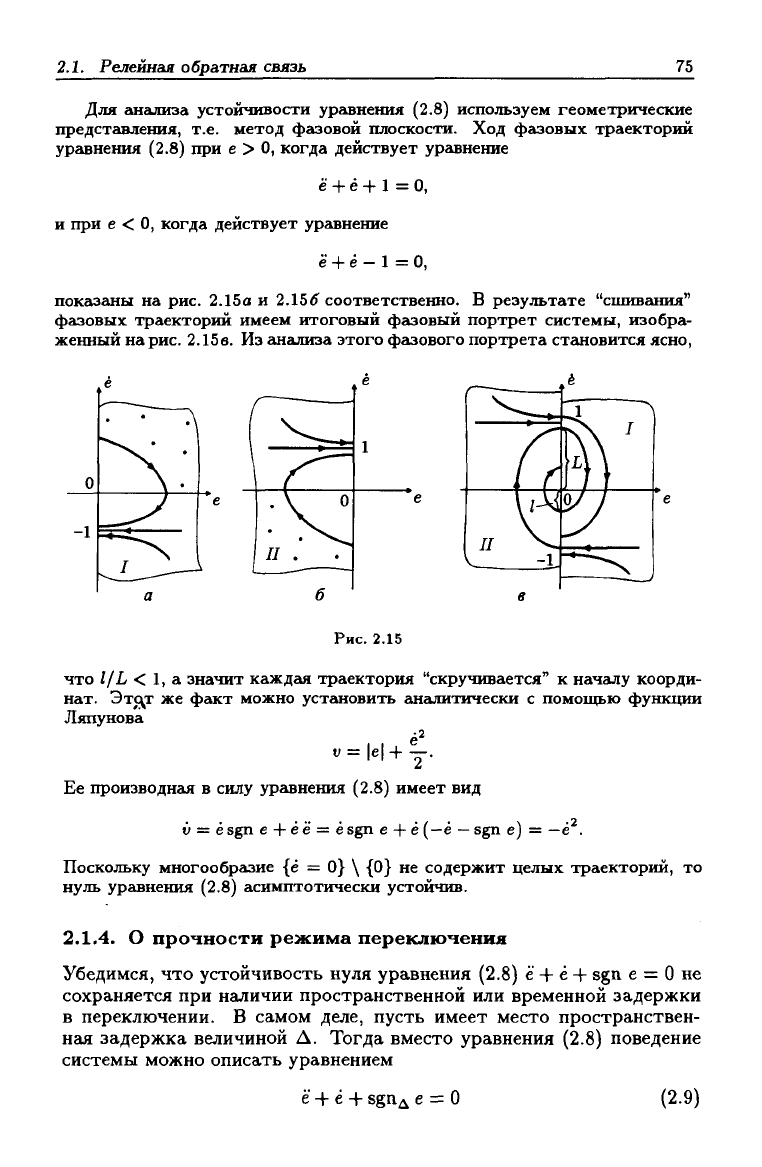
Для анёишза устойчивости уравнения (2.8) используем геометрические

представления, т.е. метод фгкзовой плоскости. Ход фазовых траекторий

уравнения (2.8) при е > О, когда действует уравнение

ё + ё +

= О,

и при е < о, когда действует уравнение

ё + ё - 1 = О,

показаны на рис. 2.15а и 2.156 соответственно. В результате "сшивания"

фазовых траекторий имеем итоговый фазовый портрет системы, изобра-

женный на рис. 2.15в. Из ангишза этого фазового портрета становится ясно.

Рис.

2.15

что 1/L < 1, а значит каждая траектория "скручивается" к началу коорди-

нат. Этс(,т же факт можно установить аналитически с помощью функции

Ляпунова

-|e|

Ее производная в силу уравнения (2.8) имеет вид

i) = esgn е -f- её = esgn е -Ь ё(—ё

—

sgn е)

• 2

-е .

Поскольку многообразие {ё = 0} \ {0} не содержит целых траекторий, то

нуль уравнения (2.8) асимптотически устойчив.

2.1.4. О прочности рехсима переключения

Убедимся, что устойчивость нуля уравнения (2.8) ё-\- ё + sgn е =

не

сохраняется при наличии пространственной или временной задержки

в переключении. В самом деле, пусть имеет место пространствен-

ная задержка величиной Д. Тогда вместо уравнения (2.8) поведение

системы можно описать уравнением

ё + ё+ sgnд е = О

(2.9)

76 Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

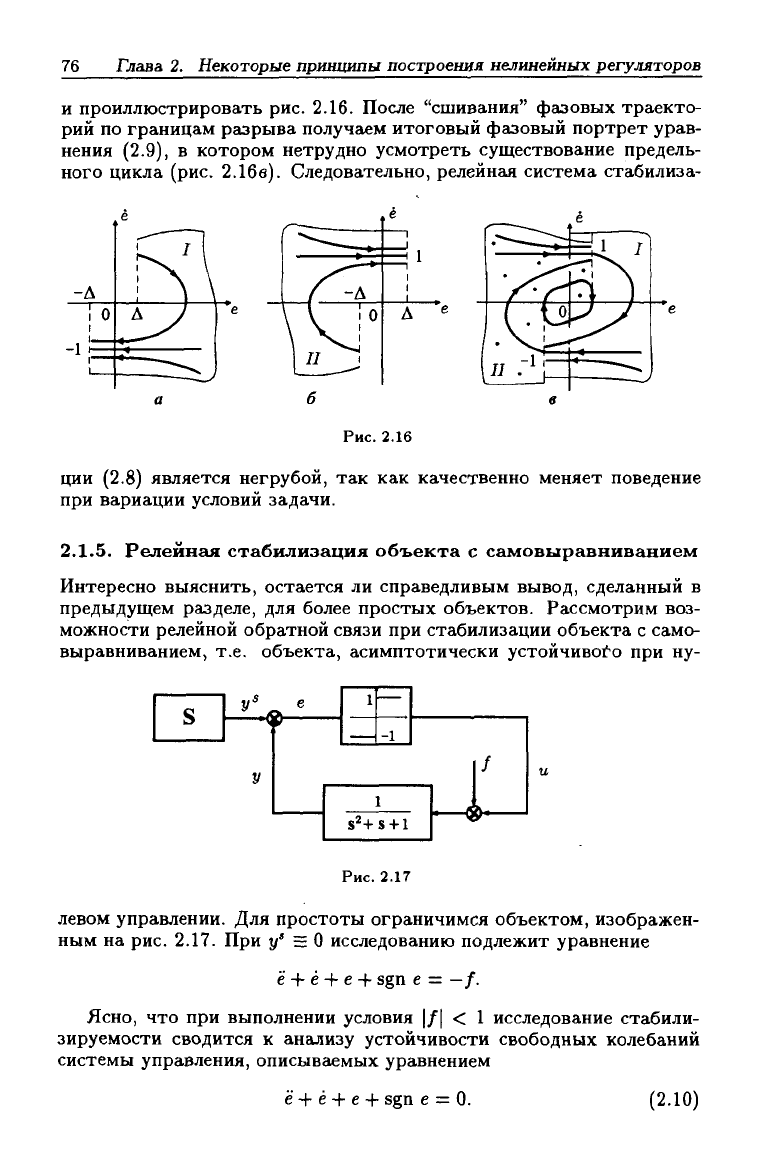
и проиллюстрировать рис. 2.16. После "сшивания" фазовых траекто-

рий по границам разрыва получаем итоговый фмовый портрет урав-

нения (2.9), в котором нетрудно усмотреть существование предель-

ного цикла (рис. 2.16в). Следовательно, релейная система стабилиза-

Рис. 2.16

ции (2.8) является негрубой, так как качественно меняет поведение

при вариации условий задачи.

2.1.5.

Релейная стабилизация объекта с самовыравниванием

Интересно выяснить, остается ли справедливым вывод, сделанный в

предыдущем разделе, для более простых объектов. Рассмотрим воз-

можности релейной обратной связи при стабилизации объекта с само-

выравниванием, т.е. объекта, асимптотически устойчивого при ну-

у« ^ е

-1

s^+s+1

' Q

Рис. 2.17

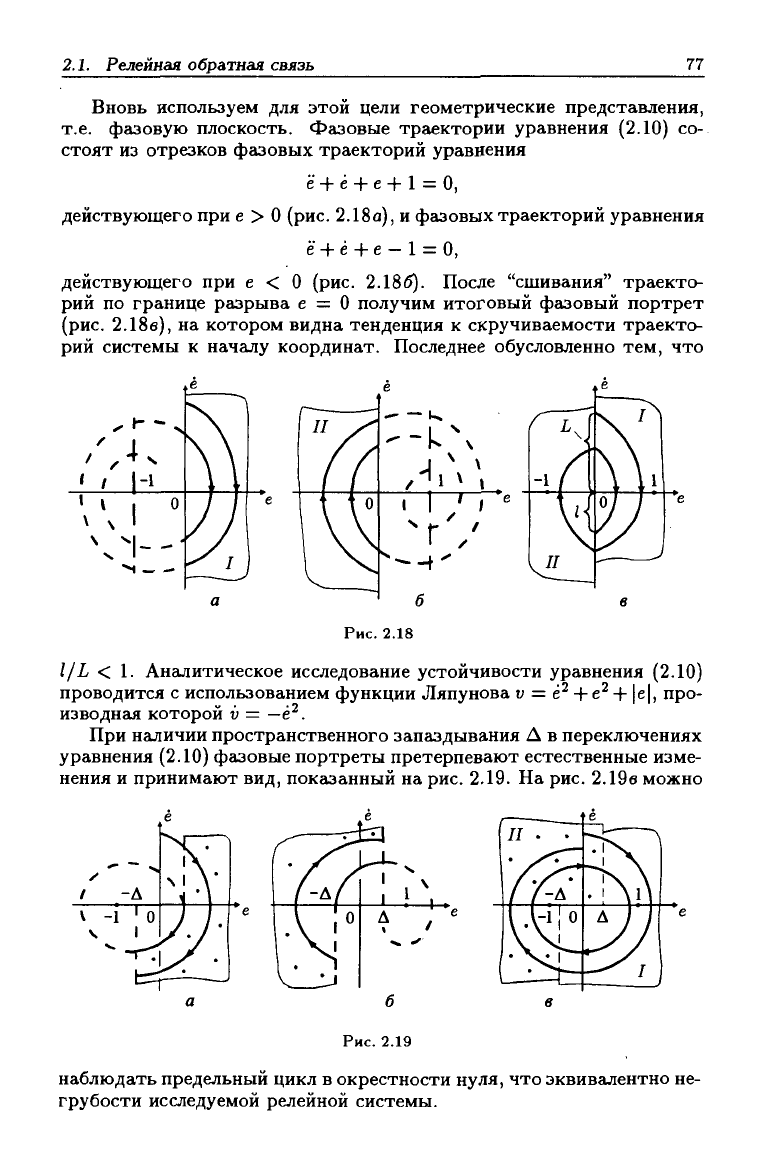
левом управлении. Для простоты ограничимся объектом, изображен-

ным на рис. 2.17. При у' =

исследованию подлежит уравнение

ё + ё + е + sgn е = —/.

Ясно,

что при выполнении условия |/| < 1 исследование стабили-

зируемости сводится к анализу устойчивости свободных колебаний

системы управления, описываемых уравнением

ё + ё + е + sgn е = 0.

(2.10)

2.1.

Релейная

обратная

связь

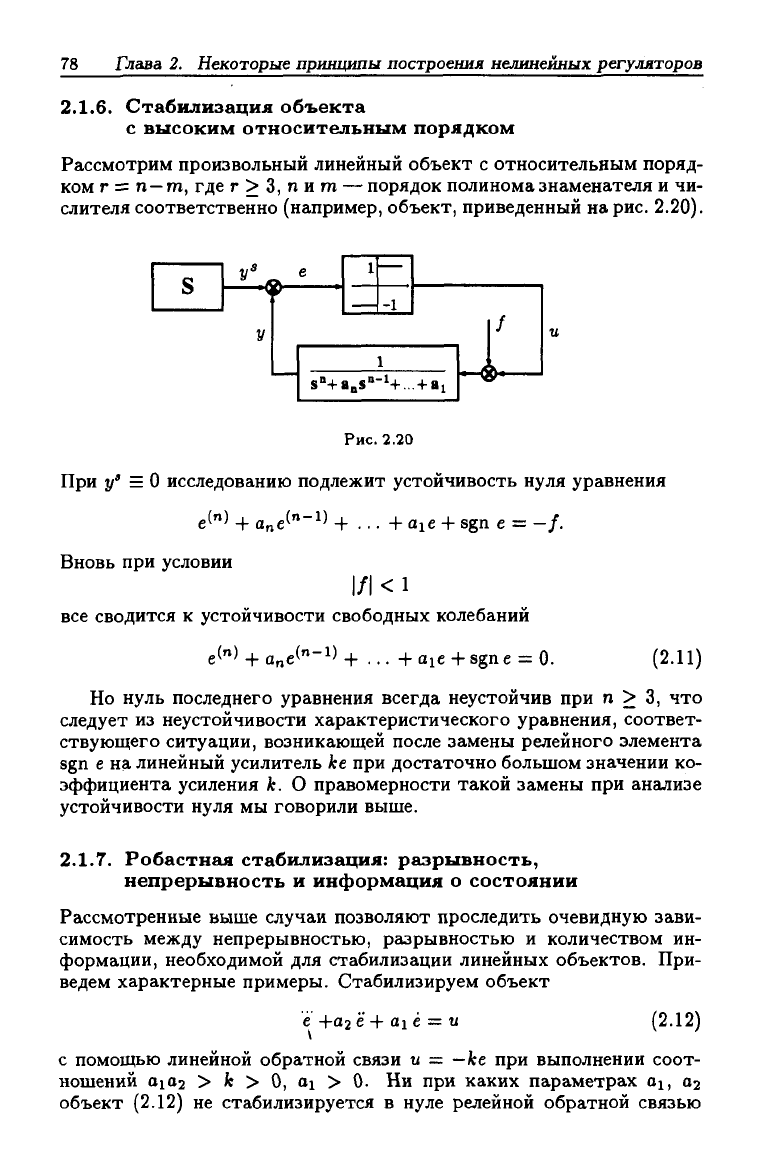
Вновь используем для этой цели геометрические представления,

т.е.

фазовую плоскость. Фазовые траектории уравнения (2.10) со-

стоят из отрезков фазовых траекторий уравнения

ё +

О,

действующего при е >

(рис. 2.18а), и фазовых траекторий уравнения

ё-|-ё-|-е-1

= 0,

действующего при е < О (рис. 2.186). После "сшивания" траекто-

рий по границе разрыва е = О получим итоговый фазовый портрет

(рис.

2.18б), на котором видна тенденция к скручиваемости траекто-

рий системы к началу координат. Последнее обусловленно тем, что

Рис.

2.18

1/L < 1. Ангшитическое исследование устойчивости уравнения (2.10)

проводится с использованием функции Ляпунова v = Р -\-е^ + \е\, про-

изводная которой i) = —ё^.

При нашичии пространственного запаздывания Д в переключениях

уравнения (2.10) фазовые портреты претерпевают естественные изме-

нения и принимают вид, показанный на рис. 2.19. На рис. 2.19в можно

наблюдать предельный цикл в окрестности нуля, что эквивалентно не-

грубости исследуемой релейной системы.

78 Глава 2. Некоторые принципы построения нелинейных регуляторов

2.1.6. Стабилизация объекта

с высоким относительным порядком

Рассмотрим произвольный линейный объект с относительным поряд-

ком г = п

—

тп,

где г > 3, п и m — порядок полинома знаменателя и чи-

слителя соответственно (например, объект, приведенный карие. 2.20).

•V

•ж

-1

s"+anS°"4.

+ ai

•—(ar——

Рис. 2.20

При у* =

исследованию подлежит устойчивость нуля уравнения

е("'

-I-

а„е("~^' -|- ... + aje -Ь sgn е = -/.

Вновь при условии

все сводится к устойчивости свободных колебаний

е(") + а„е<"~^) + ..

•

+ aie -f- sgn

= 0.

(2.11)

Но нуль последнего уравнения всегда неустойчив при п > 3, что

следует из неустойчивости характеристического уравнения, соответ-

ствующего ситуации, возникающей после замены релейного элемента

sgn е на линейный усилитель ке при достаточно большом значении ко-

эффициента усиления к. О правомерности такой замены при анализе

устойчивости нуля мы говорили выше.

2.1.7. Робастная стабилизация: разрывность,

непрерывность и информация о состоянии

Рассмотренные выше случаи позволяют проследить очевидную зави-

симость между непрерывностью, разрывностью и количеством ин-

формации, необходимой для стабилизации линейных объектов. При-

ведем характерные примеры. Стабилизируем объект

е -(-02 ё +

От

ё = и (2.12)

с помощью линейной обратной связи и — —ке при выполнении соот-

ношений 0102 > fc > О, oi > 0. Ни при каких параметрах oi, 02

объект (2.12) не стабилизируется в нуле релейной обратной связью

2.1.

Релейная

обратная

связь

U = —sgn е. Если, однако, в закон релейной обратной связи ввести

дополнительную информацию о производных е и ё, например

u = -sgn(e + e),

=-sgn(e + e + e),

то устойчивость нуля при 01,02 > о будет обеспечена. Иными сло-

вами,

• существуют ситуации, когда переход от разрывного элемента к

непрерывному, в частности, к линейному элементу не только по-

вышает прочность системы управления, но и позволяет решить

задачу при меньшем объеме информации о ее состоянии.

Аналогичная зависимость существует между прочностью системы

и непрерывностью ее нелинейных элементов. Для пояснения рассмо-

трим уравнение

ё -Ь ое 4- sgn е = О, а = const > 0.

На плоскости (е,ё) ему соответствует рис. 2.21а, со скользящим

режимом в нуле. При наличии запаздывания г в переключении раз-

рывного элемента имеем дело с уравнением

ё-Ьае-t-sgnCr = О, er=e(f-r),

которому соответствует рис. 2.216. На этом рисунке видно возникно-

вение режима переключения с предельным циклом. При достаточно

малом запаздывании

можно прибегнуть к аппроксимации е^ =

е —

гё

и вместо sgnвт использовать разрывной элемент вида sgn (е

—

те), что

не меняет качественную картину явления (рис. 2.21в). Ситуация ме-

е-гё=0

Рис. 2.21

няется качественно, если реле заменить наклоном, т.е. от р£1зрывного

элемента перейти к непрерывному элементу, например к элементу

типа насыщения.

Тогда для анализа устойчивости в нуле следует иметь дело с ли-

нейным уравнением

ё-\- ае + кбт =

О,

к = const > О,

которому соответствует характеристический квазиполином s -|- а +

+ке~''^ = 0. При достаточно большом значении коэффициента усиле-

ния к у этого уравнения всегда есть нули \{к) в правой комплексной

Глава 2.

Некоторые

принципы

построения

нелинейных регуляторов

полуплоскости, стремящиеся при к

—>

оо к нулям уравнения е~'^ = 0.

Последние, очевидно, имеют положительные вещественные части.

С другой стороны, если к конечно, а г мало, то с помощью аппрокси-

мации е"*'' к

1—ST

анализ устойчивости можно свести к исследованию

полинома первого порядка (1

— кт)

s + а +

Аг

= 0. Очевидно, что при

выполнении неравенств

1 —

А:г>0, а + Аг>0 наступает устойчивость,

т.е.

предельный цикл исчезает.

Подводя итог исследованию, можно сделать вывод о том, что ре-

лейная стабилизация годится только для объектов с относительным

порядком г < 2. Поскольку стабилизация при г = п

—

m = 2 была рас-

смотрена выше, то теперь можно исследовать особенности релейной

стабилизации при г = п

—

т = 1.

2.1.8. Робастная стабилизация объекта

с первым относительным порядком

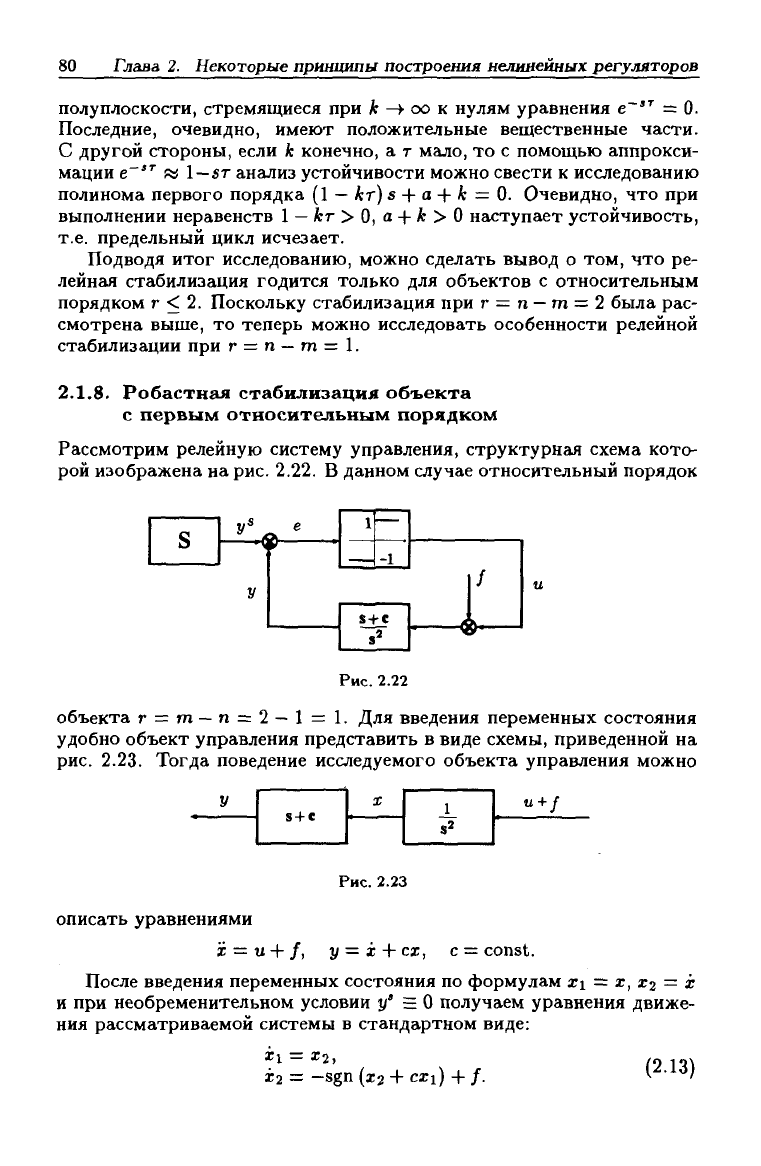
Рассмотрим релейную систему управления, структурная схема кото-

рой изображена на рис. 2.22. В данном случае относительный порядок

А.

S + C

Рис.

2.22

объекта г = т

—

п = 2—1 = 1. Для введения переменных состояния

удобно объект управления представить в виде схемы, приведенной на

рис.

2.23. Тогда поведение исследуемого объекта управления можно

S + C

U+/

Рис.

2.23

описать уравнениями

i =

/, у = х + сх,

const.

После введения переменных состояния по формулам ц = х, Х2 = х

и при необременительном условии у' =

получаем уравнения движе-

ния рассматриваемой системы в стандартном виде:

XI = Х2,

Х2 = -Sgn (Г2 -I- CXi) -I- /.

(2.13)