Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

1.6.

Метод

К-изображеиий

или

метод встроенной

модели

где К — полином из (1.27). Решая уравнение (1.29) относительно R,

находим требуемый оператор R:

(1.30)

где N = iPi- LK)/{LPiPi).

Формула (1.30) показывает, что местная обратная связь, обеспечи-

вающая условие инвариантности, должна содержать оператор, обрат-

ный оператору, аннулирующему возмущение. Именно с этим обстоя-

тельством и связано второе название описываемого метода — метод

встроенной модели.

При выполнении условия инвариантности (1.29) справедливы ра-

венства

P!i

: Pi

= LKPi ы.

1 -(- Pl^PiR

и для окончательного решения задачи стабилизации {у = у") необ-

ходимо подобрать корректирующую обратную связь по нагрузке для

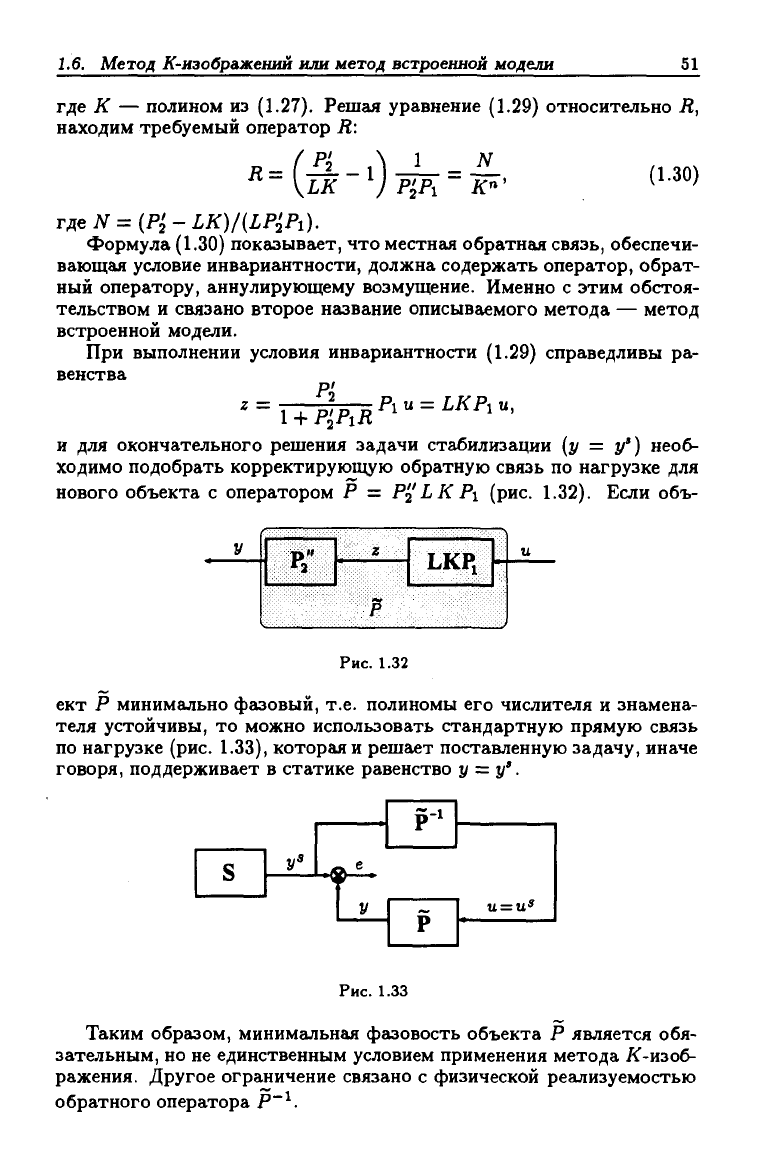
нового объекта с оператором Р =

Р!^

LKP\ (рис.

1.32).

Если объ-

Р"

LKPi

Рис. 1.32

ект Р минимально фазовый, т.е. полиномы его числителя и знамена-

теля устойчивы, то можно использовать стандартную прямую связь

по нагрузке (рис.

1.33),

которая и решает поставленную задачу, иначе

говоря, поддерживает в статике равенство у = у'.

у*

,л

•V

V-'

и = и*

Рис. 1.33

Таким образом, минимальная фазовость объекта Р является обя-

зательным, но не единственным условием применения метода /<^-изоб-

ражения. Другое ограничение связано с физической реализуемостью

обратного оператора Р~^.

Глава 1. Принципы

построения

линейных

систем

Действительно, оператор местной обратной связи R должен быть

физически осуществим, но тогда таковым обязан быть и оператор Р,

а следовательно, оператор Р~^ нереализуем. Речь может идти только

о физически реализуемой аппроксимации Р~^ оператора Р~^, и, ве-

роятно, задача стабилизации может решаться только приближенно.

Для ослг1бления требований минимальной фазовости и физической

осуществимости Р~* можно, наряду со связью по нагрузке, использо-

у'

.6» ^

•V

—4—1

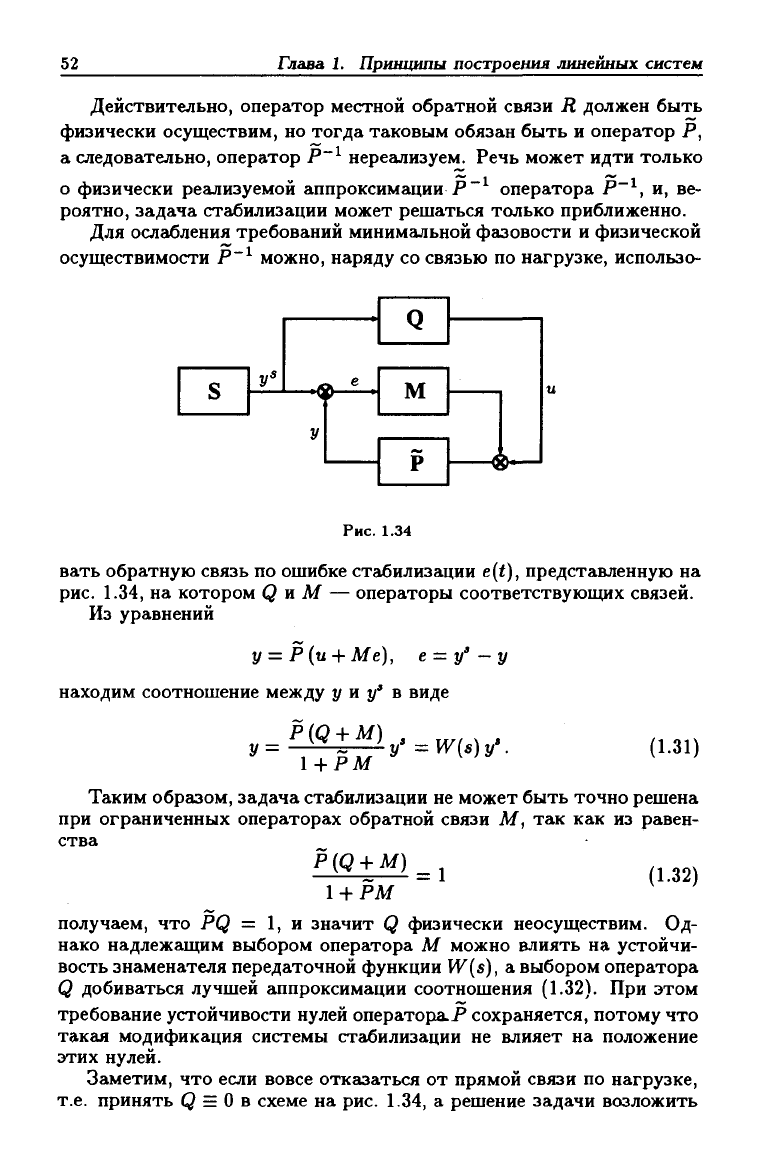
Рис. 1.34

вать обратную связь по ошибке стабилизации e{t), представленную на

рис.

1.34, на котором Q и М — операторы соответствующих связей.

Из уравнений

у = Р{и + Ме), е = у'-у

находим соотношение между у и у' в виде

У =

P{Q + M)

1+РМ

у'=Ж(«)у'.

(1.31)

Таким образом, задача стабилизации не может быть точно решена

при ограниченных операторах обратной связи М, так как из равен-

ства

P{Q + M)

= 1

(1.32)

1-1-РМ

получаем, что PQ = 1, и значит Q физически неосуществим. Од-

нако надлежащим выбором оператора М можно влиять на устойчи-

вость знаменателя передаточной функции iy(s), а выбором оператора

Q добиваться лучшей аппроксимации соотношения (1.32). При этом

требование устойчивости нулей оператора.Р сохраняется, потому что

такая модификация системы стабилизации не влияет на положение

этих нулей.

Заметим, что если вовсе отказаться от прямой связи по нагрузке,

т.е.

принять Q =

в схеме на рис. 1.34, а решение задачи возложить

1.6. Метод К-иэображений

или

метод встроенной модели

на обратную связь, то получим такое соотношение между у и у':

РМ ,

=—У

1 + РМ

Ясно,

что только при условии \РМ\ 3> 1 можно рассчитывать на удо-

влетворительное решение задачи стабилизации.

Но это уже другая тема — тема глубокой обратной связи, к кото-

рой мы перейдем в следующем разделе, а теперь рассмотрим пример

к методу 7<Г-изображения.

Пример

Стабилизация методом ЛГ-изображения. Ознакомим-

ся

возможностями

недостатками метода /("-изображения

при

работе

передаточными функциями

и в

пространстве состояний. Рассмотрим слу-

чаи постоянного

экспоненциального возмущения.

Случай

. Пусть возмущение

/ =

const действует

на

объект согласно

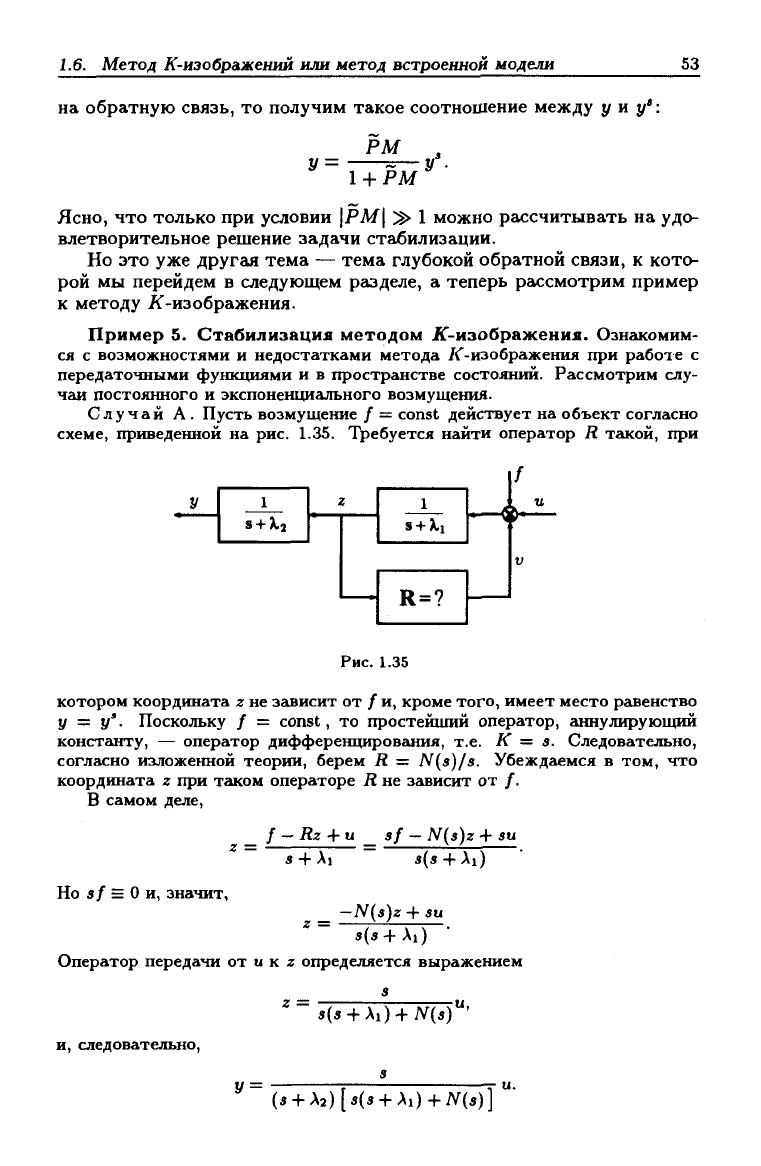
схеме, приведенной

на рис. 1.35.

Требуется найти оператор

такой,

при

s + Xj

s + Xi

R = ?

Рис.

1.35

котором координата

г не

зависит

от / и,

кроме того, имеет место ргшенство

•=.

у'.

Поскольку

/ =

const,

то

простейший оператор, аннулирующий

константу,

—

оператор дифференцирования,

т.е. К = з.

Следовательно,

согласно изложенной теории, берем

R =

N{s)/s. Убеждаемся

в том, что

координата

z при

таком операторе

R не

зависит

от /.

В самом деле,

f -Rz + u _ sf - N{s)z + su

a/ = 0

И, значит,

_ —N{s)z

+ su

'~ S(5-|-Al)

Оператор передачи

от u к г

определяется выражением

s{s^•\^)^•N{s)

и, следовательно,

(5 + A2)[s(5+Al)-(-iV(s)]

Глава 1. Принципы построения линейных систем

Если попытаться обеспечить равенство операторов Р ~ Р, т.е.

S 1

(*+A2)[5(5 + Al) + iV(5)] " (e + A2)(« + Al)'

то с неизбежностью получим N(s) = 0. Поэтому направим выбор оператора

N{3) на достижение устойчивости "подновленного" объекта Р или, что то

же самое, при устойчивом объекте Р — на устойчивость полинома

,fi(s) = s(3 + Xi) + N{s).

Устойчивость полинома достигается, например, при N = к = const > О,

так как в итоге получаем (^(s) = s^ +

3X1

+ к. При Ai > О (это условие

выполнено по предположению) и fc >

этот полином — гурвицев.

S + X2

S + X.1

Ai •

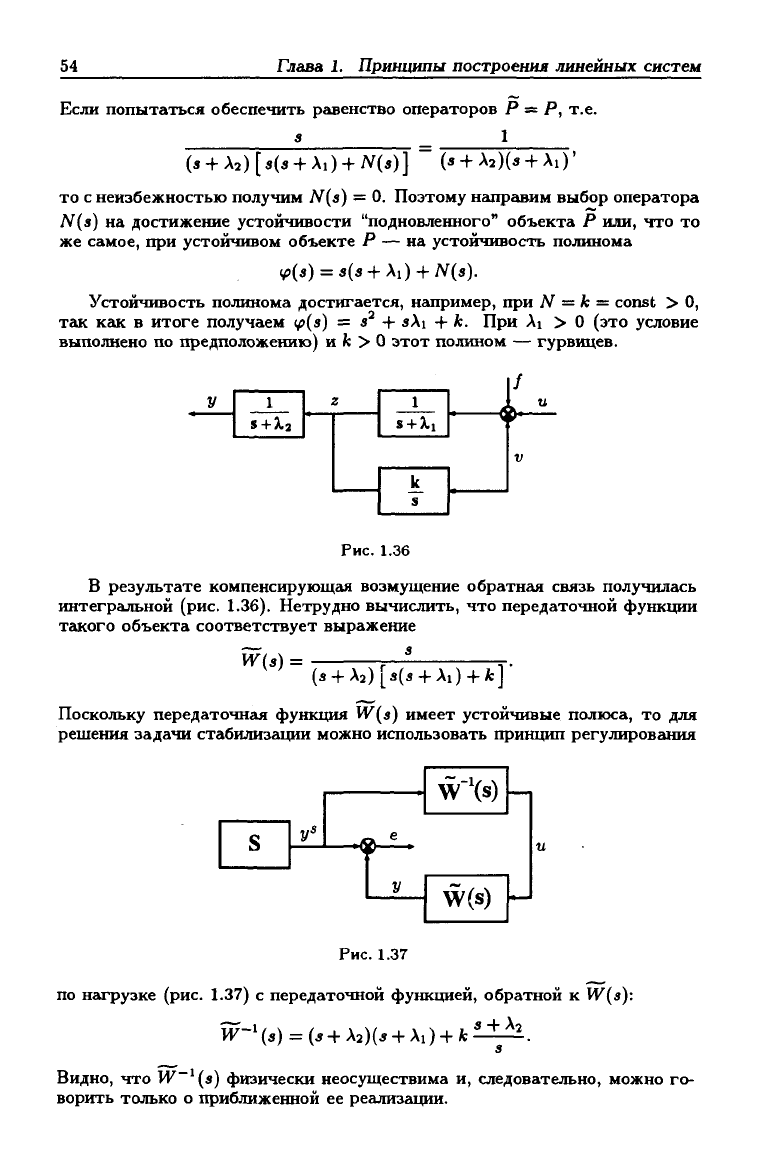
Рис.

1.36

В результате компенсирующем возмущение обратная связь получилась

интегральной (рис.

1.36).

Нетрудно вычислить, что передаточной функции

такого объекта соответствует выражение

W{s) = *

(e + A2)[s(e + Ai) +

*:]'

Поскольку передаточная функция W{s) имеет устойчивые полюса, то для

решения задачи стабилизации можно использовать принцип регулирования

у'

о. е

W-^s)

W(s)

Рис.

1.37

по нагрузке (рис. 1.37) с передаточной функцией, обратной к W(s):

цг-\з) ^ (3 + Х2)(з + Xi) + к

А2

Видно, что W ' (s) физически неосуществима и, следовательно, можно го-

ворить только о приближенной ее реализации.

1.6. Метод К-изображений или метод встроенной модели 55

Случай Б. Задача становится неразрешимой этим методом, если на

входе объекта действует экспоненцигшьное возмущение / = е°*, а — const.

Аннулирующим для f{t) является оператор К = s

—

а. Действительно,

/./=(^/-./)

= а/ - а/ = 0.

Следуя рекомендациям теории, получаем

N{s)ls-a,

и связь между гни определяется выражением

(д-а)

' (з-аКз + АО + Ща)"'

Выбираем оператор ЛГ(з) из соображении устойчивости полинома

¥>(s) = (в-a)(s-(-Ai

)

+ iV(s).

Ясно,

что можно положить N{s) = k\s -{-ki. Тогда при выполнении нера-

венств fci > Ai а, /гг > а

—

Ai рассматриваемый полином <;>(«) — гурвицев.

В результате передаточная функция "подновленного" объекта опреде-

ляется выражением

^^'^ = (ТТА^Ы^'

а обратная

ней передаточная функция

-1,

(з-ЬА2)у(з)

имеет неустойчивый полюс, и, значит, в данном случае принцип регули-

рования по нагрузке применять нельзя. Ничего в этой схеме не меняет и

обратная связь по ошибке е = у' — у,

тала

как такгш связь не устраняет-

правых нулей передаточных функций.

Случай В. Вновь рассмотрим объект, представленный структурной

схемой на рис. 1.35 с возмущением / = const, но теперь для описания метода

/^-изображения используем дифференциальные уравнения. Дгинный объект

описывскется дифференциальными уравнениями

+ \2У = г,

z + Xiz = f + u-v. (1.33)

После дифференцирования по t уравнения (1.33) с учетом того, что / = О,

имеем

Xi Z =

+ й,

и, следовательно, z не зависит от /. Полагаем

«>

= kz. (1.34)

Тогда

\i Z + kz = й,п если

А;

> О, то это уравнение устойчиво и надле-

жащим выбором й(у') можно получить у

—>

у', что решг1ет задачу. Урав-

нение (1.34) описывает интегргшьную обратную связь, так как

'"1

zdt.

Глава 1. Принципы

построения

линейных

систем

1.7. Глубокая обратная связь

—

большой коэффициент усиления

Рассмотрим один из наиболее мощных методов решения задач ста-

билизации в условиях неопределенности — метод глубокой обратной

связи, который для линейного случая сводится к использованию в ре-

гуляторе большого коэффициента усиления.

1.7.1. Постановка задачи, особенности и идея решения

Пусть на объект с оператором Р = Pi Рг действует возмущение /

(рис.

1.38).

Требуется выбором управления и обеспечить независи-

Рг

Рис. 1.38

мость регулируемой координаты у от возмущения / и, кроме того,

достижение и поддержание равенства

= «/'•

Укажем на некоторые особенности постановки задачи стабилиза-

ции. Во-первых, не предполагается, как ранее, что объект Р обяза-

тельно устойчивый. Во-вторых, возмущение / необязательно является

малым или исчезающим со временем. И, наконец, в-третьих, не пред-

полагается наличие возможностей прямого или косвенного измерения

возмущения /.

В рассматриваемых условиях применение описанных выше мето-

дов невозможно, а потому неизбежно обращение или к обратной связи

и принципу регулирования по ошибке в рамках схемы на рис. 1.39, в

которой надлежит выбрать оператор обратной связи R', или к со-

Jil.A—£.

'.-4U"

Рг

Рис. 1.39

1.7. Глубокая

обратная

связь

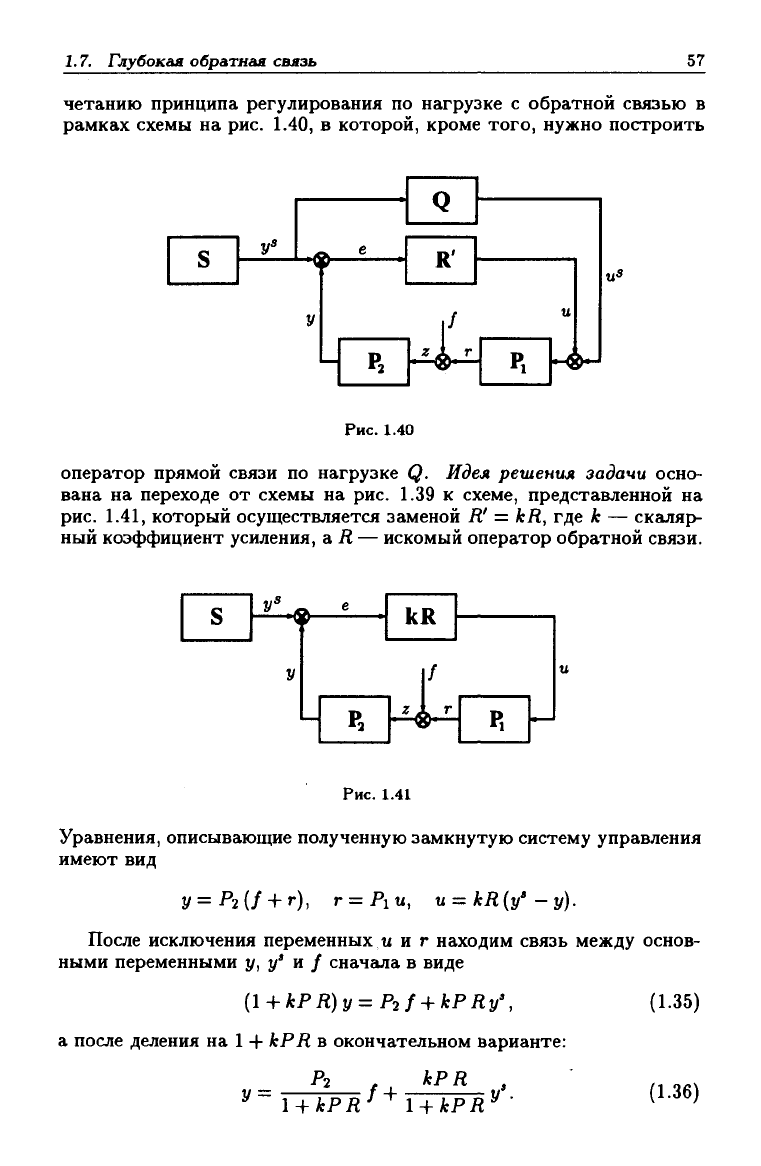
четанию принципа регулирования по нагрузке с обратной связью в

рамках схемы на рис. 1.40, в которой, кроме того, нужно построить

Рис.

1.40

оператор прямой связи по нагрузке Q. Идея решения задаии осно-

вана на переходе от схемы на рис. 1.39 к схеме, представленной на

рис.

1.41, который осуществляется заменой R' = kR, где к — скаляр-

ный коэффициент усиления, а Я — искомый оператор обратной связи.

У" .^ е

•«

-4-4^

Рис.

1.41

Уравнения, описывающие полученную замкнутую систему управления

имеют вид

y = P2{f + r), r = Piu, u = kR(y'-y).

После исключения переменных и и г находим связь между основ-

ными переменными у, у' л f сначала в виде

il+kPR)y = P2f + kPRy',

а после деления на

-|- kPR в окончательном варианте:

Рг , , kPR ,

\ + kPR' l + kPR

(1.35)

(1.36)

58 Глава 1. Принципы построения линейных

систем

Можно заметить, что при к

—^

оо первое слагаемое в выражении

(1.36) уменьшается до нуля, а второе стремится к заданию у', что

и решает рассматриваемую задачу стабилизации, если, конечно, при

каждом значении к -¥ оо замкнутая система асимптотически устой-

чива.

Кроме того, использование больших коэффициентов усиления ве-

дет к увеличению значений переменных системы, а поскольку в реаль-

ных системах всегда имеются амплитудные ограничения, то необхо-

димо изучить их влияние на свойства системы. Наконец, следует выяс-

нить,

насколько чувствительно решение, даваемое глубокой обратной

связью, к вариациям условий задачи, т.е. по отношению к регуляр-

ным и сингулярным возмущениям. Свойства системы, непрерывно

зависящие от указанных возмущений, принято называть грубыми.

1.7.2. Проблемы и ограничения

метода глубокой обратной связи

В этом и последующих разделах рассмотрим некоторые из упомяну-

тых выше проблем. Здесь мы исследуем условия устойчивости пре-

дельной и допредельной систем и изучим влияние амплитудных огра-

ничений на управление.

Из уравнения (1.36) замкнутой системы получаем

{l+kPR)y = P2f + kPRy',

и, следовательно, при к —^ оо нужно изучать устойчивость свобод-

ного движения или, что то же самое, устойчивость нулевого решения

уравнения

{l + kPR)y = 0. (1.37)

Обозначим передаточную функцию объекта Р через

W ( ) -

^"'+1^"'

+ ^mg"'"^ + ...+bi _ b{s)

•^^^"^ s" + a„s"-'+ ...+ai a{s)'

a передаточную функцию регулятора R, — как

Pn +

lS"

+ PnS"~^ +

•••+?!

P(s)

Wnis)

9n+is"+9„s"-i-(-... -f-gi q(s)'

Подстановка этих выражений в исследуемое уравнение (1.37) дает

выражение

a(s) q{s)

_ a[s)q{s) + kb{s)p{s)

a{s)q{s) У'

и проблема устойчивости сводится к исследованию при fc

—^

оо гур-

вицевости параметрического семейства полиномов

<Pkis)

= a{s)q{s)+kb{s)p{s) = v?a,<,(s) +V'b,p(s)- (1-38)

1.7. Глубокая

обратная

связь 59

Из (1.38) следует, что при fc -> оо часть нулей исследуемого поли-

нома совпадает с нулями полинома

ipb^p(s),

которые, конечно, должны

иметь отрицательные вещественные чг1сти, и это первое ограничение

метода. Далее, по условию физической осуществимости, степень по-

линома числителя меньше степени полинома знаменателя, т.е.

deg (pk{s) < deg

<Pa,q{s),

(1.39)

и, следовательно, полином

(роо

(«) помимо нулей полинома

(pb,p(s)

имеет

другие нули, которые также должны принадлежать открытой левой

полуплоскости переменной s. Из анализа допредельного полинома

(1.38) видно, что абсолютные значения его нулей A,(fc), не стремя-

щихся при fc -> 00 к нулям полинома

(рь,р{з),

увеличиваются до беско-

нечности, так как при любом к должно выполняться равенство

^Pk{Xkik)) =a{Xkik))q{Xkik)) +kb{X,(k))p{Xk{k)) =0.

Ясно,

что по соображению устойчивости эти нули при к

—^

оо должны

уходить в бесконечность в левой открытой полуплоскости комплекс-

ной переменной s, и это — второе ограничение данного метода.

Для выражения условия (1.39) через параметры системы поделим

с помощью алгоритма Евклида полином

'Pa,q{s)

= a(s) q(s) на полином

(pb,p(s).

В результате получим равенство

a{s) b{s) = e{s) b{s) p{s) + r{s), (1.40)

где 0(s) — чги:тное, a r(s) — остаток деления, причем его степень

меньше степени делителя, т.е.

deg r(s)< deg (b(s)p(s)). (1.41)

Используя равенство (1.40), представим полином

<Pk(s)

в виде

<Pk(s)

=:b(s)p(s)

b(s)p(s)

Теперь ясно, что бесконечно растущие при fc —> оо нули полинома

fkls) стремятся к нулям полинома

d{s) = e{s)+k,

так как по доказанному выше и в силу неравенства (141) имеет место

"'-*«> b{Xi{k))p{Xi{k))

•

Таким образом, к устойчивости полинома Vfc(s) при к -^ оо и

устойчивом полиноме

<Pb,p(s)

ведут только две возможности:

если deg Q{s) — 1, т.е. 0(s) = Gjs -|- 0i, то 63 > 0;

если deg Q{s) = 2, т.е. Q{s) = Gss^

-I-

02*

-I-

0i, то 02 > 0, 0з > 0.

Прочие же ситуации, в том числе и deg 0(s) > 2, ведут к неустойчи-

вости.

Глава 1. Принципы построения линейных систем

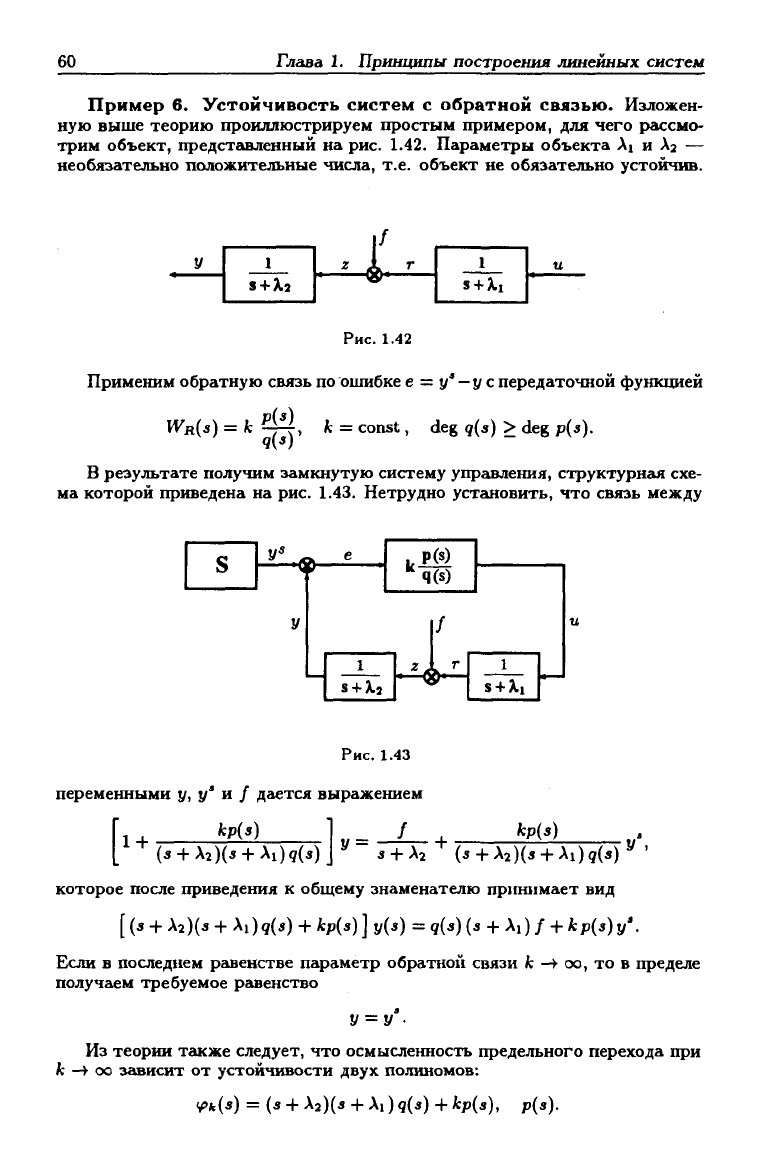
Пример е. Устойчивость систем с обратной связью. Изложен-

ную выше теорию проиллюстрируем простым примером, для чего рассмо-

трим объект, представленный на рис. 1.42. Параметры объекта Ai и Лг —

необязательно положительные числа, т.е. объект не обязательно устойчив.

s + Xj

лч

s + Xi

Рис.

1.42

Применим обратную связь по ошибке е = у' —у с передаточной функцией

WR{S)

= к 44, к = const, deg д{з) > deg р(з).

Я(»)

В результате получим замкнутую систему управления, структурная схе-

ма которой приведена на рис. 1.43. Нетрудно устгшовить, что связь между

у«

+ X2

(S)

"4(8)

s + Xi

Рис.

1.43

переменными у, у'

f дается выражением

1 +

кр(з)

{s-\-Xi){s-\-\x)q{s)

-I-

kp(s)

e-l-Ai («-(-A2)(3-hAi)g(4) " '

которое после приведения к общему знаменателю пртшмает вид

[ (л -I- Х2){з -(- А,)q{s) + kp{s)

]

y{s) = q{s) (s + X^) f + кр{з) у'.

Если в последнем равенстве параметр обратной связи fc

—>•

оо, то в пределе

получаем требуемое ргшенство

= У'-

Из теории также следует, что осмысленность предельного перехода при

—>

оо зависит от устойчивости двух полиномов:

<fik(,s)

= {з + Х2){з + Xi) д{з)

-И

кр(з), р{з).