Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

7.6. Разрывная ОК-связь 241

7.6.2. Скользящие рехсимы 2-го порядка в ОК-контуре

Рассмотрим здесь тот случай финитной стабилизации ошибки ОК-

контура и, который естественно возникает при использовании раз-

рывной ОК-связи следующего вида:

Г]

= -к2sgn iv+ х/[Нsgnf j •

(7.34)

Опуская, ввиду аналогичности, рассуждения, устанавливающие

финитность возникновения скользящего режима в точке ^ = О, перехо-

дим непосредственно к анализу уравнений скольжения в (/i,e)-npocT-

ранстве или, иначе, уравнений Е^рсистемы. При 6 = const имеем

уравнения

ди =

Ьи

+ е,

(7.35)

-k2bsgn ^/i-b v/Rsgn f^)

При получении этих уравнений учтено, что i/ = — g/i.

Уравнения, подобные уравнениям Е^рсистемы, подробно изуча-

лись в оптимально-релейных системах, сходные уравнения рассматри-

вались и в главе 5 при анализе скользящих режимов высших порядков.

Сшивание фс1зовых траекторий Ед- (рис. 7.12а) и Еь- (рис. 7.126) си-

стем в пространстве

(/i,/i)

по линии ргизрыва

^ = /i +

VAH

sgn р =

(7.36)

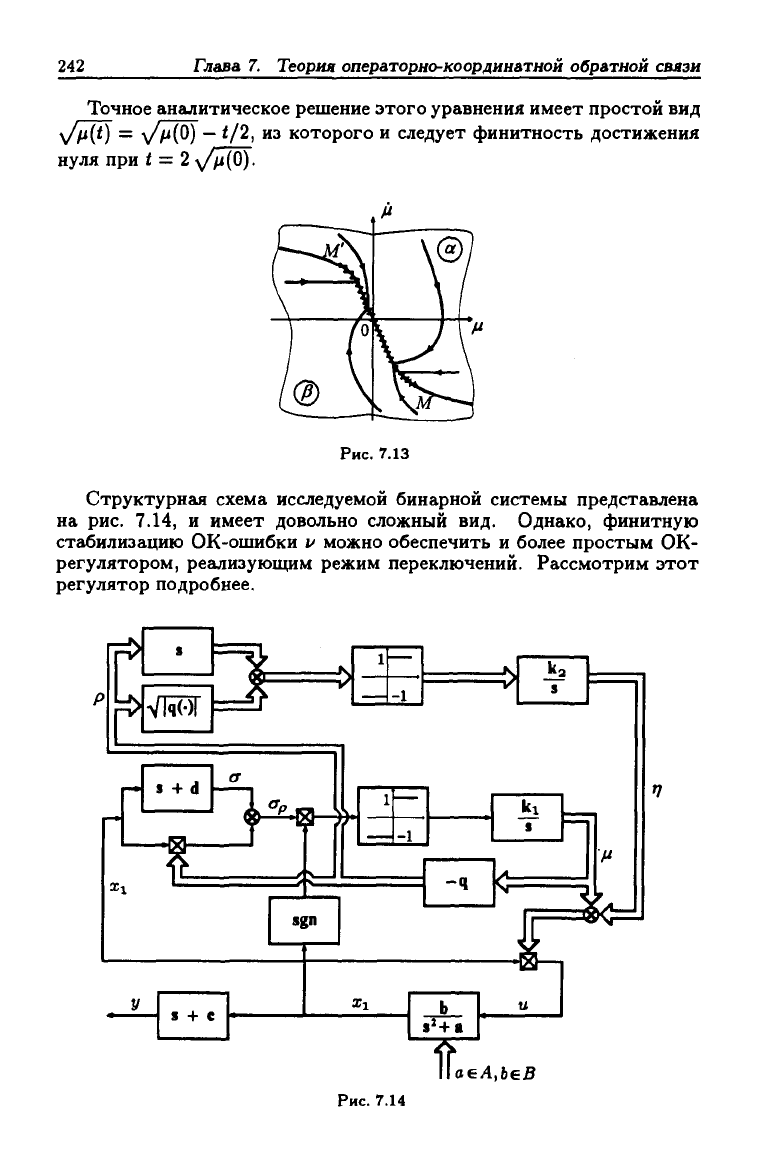
дает исходный фгйовый портрет Е^рсистемы (рис. 7.13). Из этих

\ V

Рис. 7.12

рисунков можно увидеть, что существует отрезок ММ' "параболы"

^ = /i + \/Ы sgn /i = О, в окрестности которого фазовые траекто-

рии направлены встречно, т.е. на этом отрезке возникает скользящий

режим с уравнением движения /i =

—

\/|Й ^g"

^^•

242

Глава 7. Теория

операторно-координатной обратной

связи

Точное аналитическое решение этого уравнения имеет простой вид

\/fi{i) =

y/i^iO)

—

t/2, из которого и следует финитность достижения

нуля при t = 2

^fi{0).

Рис. 7.13

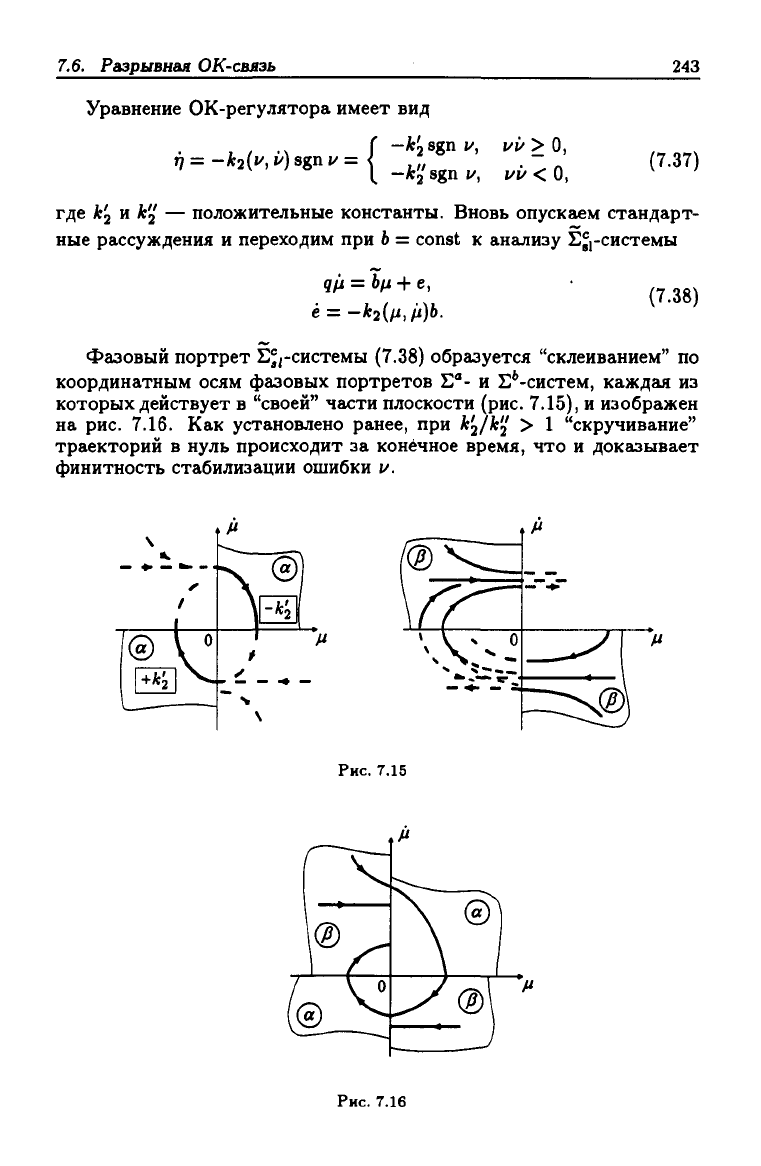
Структурная схема исследуемой бинарной системы представлена

на рис. 7.14, и имеет довольно сложный вид. Однако, финитную

стабилизацию ОК-ошибки и можно обеспечить и более простым ОК-

регулятором, реализующим режим переключений. Рассмотрим этот

регулятор подробнее.

Vlqor

I— S + d

sgn

-ч

зЫ

» + с

Рис. 7.14

s'+a

обЛ,Ье5

7.6. Разрывная ОК-свяэь

243

Уравнение ОК-регулятора имеет вид

I -*2 Sgn «^,

i/i'>0,

uu< 0,

(7.37)

где ^2 и *2 — положительные константы. Вновь опускаем стандарт-

ные рассуждения и переходим при

= const к анализу Е^рсистемы

ё = -k2{ti,ii)b.

(7.38)

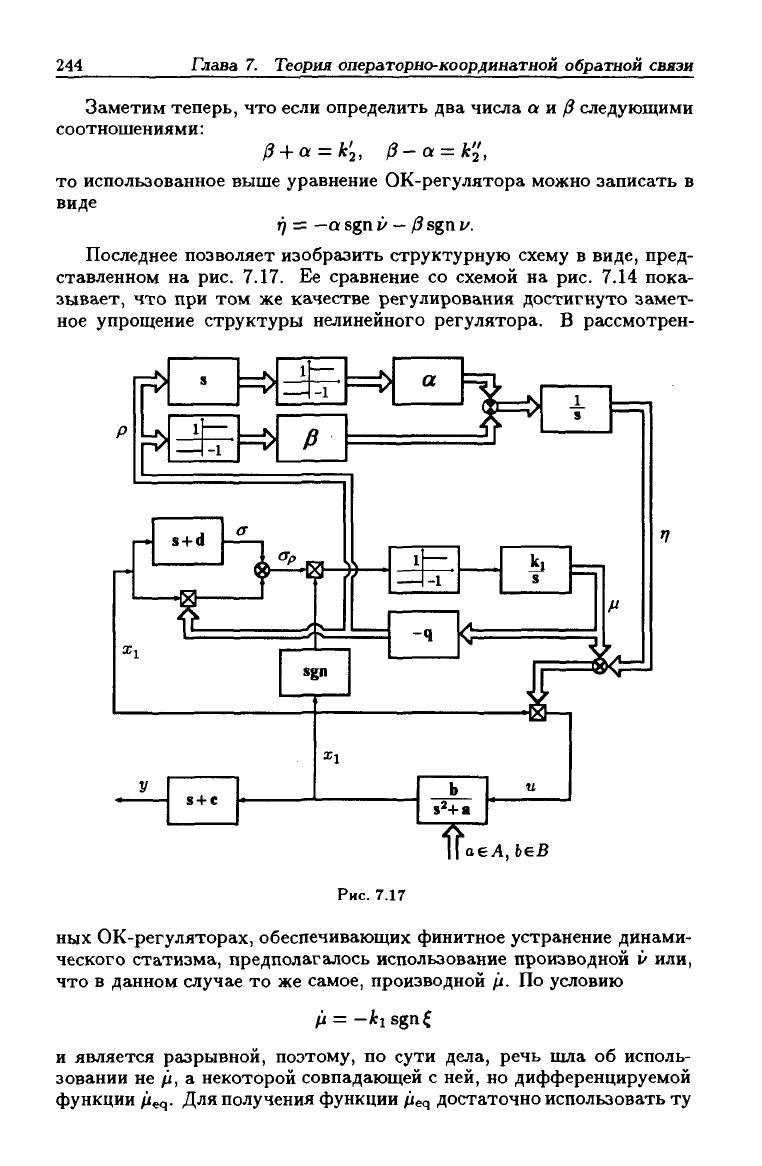
Фазовый портрет EJj-системы (7.38) образуется "склеиванием" по

координатным осям фазовых портретов Е"- и Е^-систем, каждая из

которых действует в "своей" части плоскости (рис. 7.15), и изображен

на рис. 7.16. Как установлено ранее, при кук!^ > 1 "скручивание"

траекторий в нуль происходит за конечное время, что и доказывает

финитность стабилизации ошибки i/.

—

:=:::N^

Рис. 7.15

Рис. 7.16

244

Глава 7. Теория операторно-координатной обратной связи

Заметим теперь, что если определить два числа а и /? следующими

соотношениями:

р + а =

к!2,

р-а = Щ,

то использованное выше уравнение ОК-регулятора можно записать в

виде

^ =

—а

sgn

—

/? sgn и.

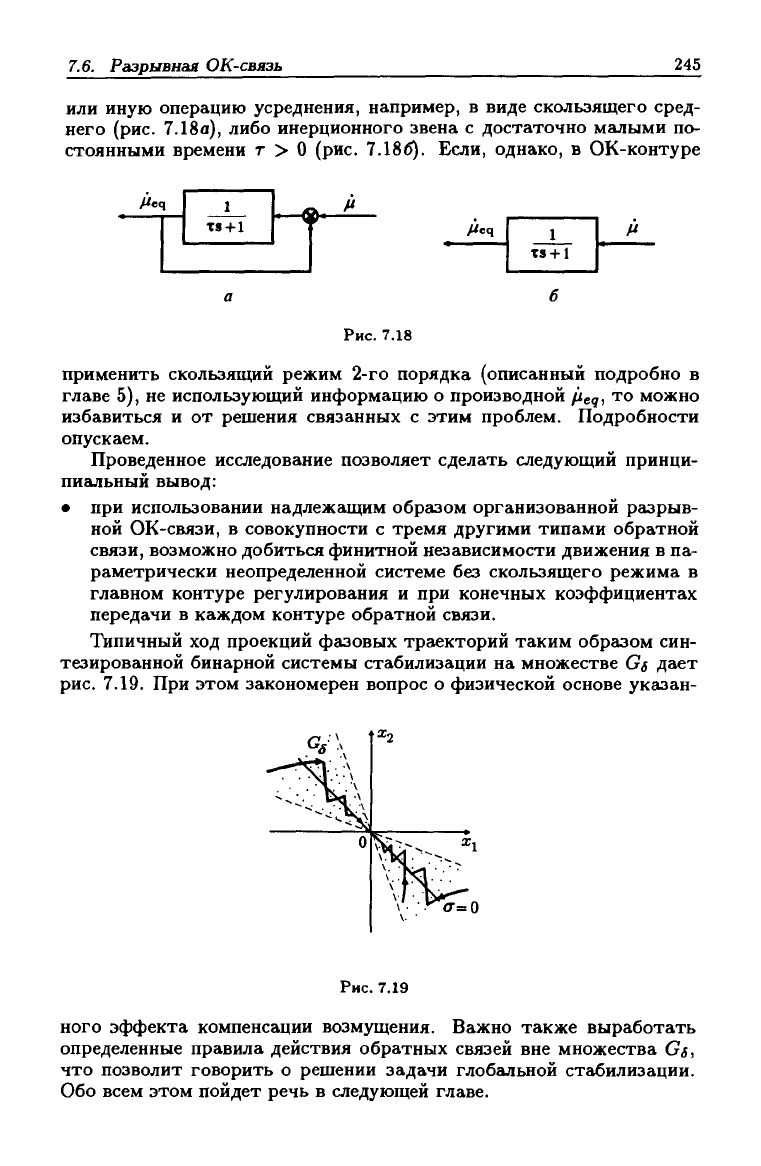
Последнее позволяет изобразить структурную схему в виде, пред-

ставленном на рис. 7.17. Ее сравнение со схемой на рис. 7.14 пока-

зывает, что при том же качестве регулирования достигнуто замет-

ное упрощение структуры нелинейного регулятора. В рассмотрен-

-1

•-• s + d

"i^

sgn

s + c

" "^ I 1

-Ч

^C=-

aeA. ЬбВ

Рис.

7.17

ных ОК-регуляторах, обеспечивающих финитное устранение динами-

ческого статизма, предполагалось использование производной v или,

что в данном случае то же самое, производной /i. По условию

/i= -ki sgni

и является разрывной, поэтому, по сути дела, речь шла об исполь-

зовании не /i, а некоторой совпадающей с ней, но дифференцируемой

функции /ieq. Для получения функции /ieq достаточно использовать ту

7.6. Разрывная ОК-связь

245

или иную операцию усреднения, например, в виде скользящего сред-

него (рис. 7.18а), либо инерционного звена с достаточно малыми по-

стоянными времени г > О (рис. 7.186). Если, однако, в ОК-контуре

М'ч

TS+1

•^

Aeq

TS +

Рис. 7.18

применить скользящий режим 2-го порядка (описанный подробно в

главе 5), не использующий информацию о производной /ieg, то можно

избавиться и от решения связанных с этим проблем. Подробности

опускаем.

Проведенное исследование позволяет сделать следующий принци-

пиальный вывод:

• при использовании надлежащим образом организованной разрыв-

ной ОК-связи, в совокупности с тремя другими типами обратной

связи, возможно добиться финитной независимости движения в па-

раметрически неопределенной системе без скользящего режима в

главном контуре регулирования и при конечных коэффициентах

передачи в каждом контуре обратной связи.

Типичный ход проекций фазовых траекторий таким образом син-

тезированной бинарной системы стабилизации на множестве Gg дает

рис.

7.19. При этом закономерен вопрос о физической основе указан-

Рис. 7.19

ного эффекта компенсации возмущения. Важно также выработать

определенные правила действия обратных связей вне множества Gs,

что позволит говорить о решении задачи глобальной стабилизации.

Обо всем этом пойдет речь в следующей главе.

Глава 8

Ограничения, физические основы

компенсации возмущений

и стабилизация вынужденного движения

в бинарных системах

До сих пор при синтезе систем стабилизации рассматривалось дви-

жение только на множестве G* =

{

а;

| |<т| < Ji^i)} (рис. 8.1), причем

число S >

считалось столь малым, что это позволяло обойтись при

анализе уравнениями первого приближения. В этой связи уместен

а=0

Рис. 8.1

первый вопрос:

• Как правильно модифицировать алгоритм бинарного управления,

с тем чтобы он был пригоден к использованию при любых началь-

ных условиях? (Разумеется, все его стабилизирующие свойства

должны сохраняться.)

Важным тезисом, бывшим одним из основных при развитии тео-

рии бинарного управления, является тезис об ограниченности коэф-

фициентов передачи и непрерывности сигналов управления и прежде

всего в главном К-контуре регулирования. Поэтому возникает вто-

рой вопрос:

• Как эти фундаментальные требования отразить в гигоритме би-

нарного управления и какими побочными эффектами это сопрово-

ждается?

Следующий, третий вопрос, на который далее дается ответ, свя-

зан с выяснением,

• какова физическая основа компенсирующего неопределенность эф-

фекта в бинарных системах.

8.1.

Ограничения

операторной

перемениой

247

Известно, что в линейных системах такой основой служит беспре-

дельное увеличение коэффициента обратной связи, в разрывных си-

стемах (СПС, релейные системы) — скользящий режим. Но в бинар-

ных системах может и не быть скодьзящего режима, а коэффициенты

передачи конечны, поэтому и возникает сформулированный выше тре-

тий вопрос. Наконец, следует прояснить четвертый вопрос:

• о тех изменениях, которые нужно внести в бинарную обратную

связь, с тем чтобы распространить ее стабилизирующие свойства

на задачи управления вынужденным движением при отсутствии

детальной информации о координатном возмущении,

т.е.

имеется в виду рассмотреть проблему стабилизации следующего

объекта:

X2 = axi + bu + f, аеА, ЬеВ, feF.

8.1.

Ограничения операторной переменной

Начнем рассмотрение со второго вопроса.

В синтезированных бинарных системах сигнал управления опреде-

ляется выражениями и = цхх либо и' = {fi + Tf)xi. Очевидно, что fi

или (/i -I-

Г])

можно интерпретировать как коэффициент передачи К-

регулятора по переменной xi. Поэтому по соображениям прочности

0-переменные /лиг) должны быть ограничены, т.е. при всех t >

\n(t)\

< const, |r;(t)| < const.

Практически удобно иметь дело с ограничениями вида

И<1,

Ы<1,

фактически же fi{t) и

T){t)

— выходные переменные некоторой динами-

ческой системы (КО- и ОК-регулятора соответственно), и проблема

ограничения такой переменной вовсе не тривиальна и требует вни-

мательного анализа. Кстати, не годится для этой цели, казалось бы,

очевидный способ ограничения с использованием сатуратора.

Действительно, соответствующая этому предложению возможная

структурная схема представлена на рис. 8.2. Уравнения системы, изо-

sat

—

-1

Рис. 8.2

248

Глава 8. Ограничения, физические основы компенсации

браженной на рис. 8.2, имеют вид

/i = -fcisgn^, /I = sat(/i)

~W. М<1.

(8.1)

Теперь в уравнении изменения 0-переменной ^ должна фигурировать

переменная /I, а не /х, как ранее, так как и = JTx, и поэтому

^ = 2rf^ +

6/H-a.

(8.2)

В результате дифференцирования ц, из (8.1) видно, что fi = fi

только при \ц\ < 1и/1=0в остальных случаях. Это качественно

меняет задачу стабилизации объекта (8.2) управлением /I и ведет к

негативным последствиям, так как при |

/х

| > 1 этот объект неупра-

вляем. Поэтому следует искать более "хитрые" решения задачи об

ограничении операторной переменной fi.

Рассмотрим ряд способов ограничения 0-переменной //, сохраня-

ющие управляемость объекта ^

—

2d^ + bfi + а.

Способ I. Положим

-ШЦ,

|/j|

> 1,

-fcsgn^, |я| < 1,

(8.3)

где ш,к — положительные константы. Если ^>0и|//|<1,то/< = —к

и fi линейно убывает до значения /х =

—

при переходе через ц = —\

уравнение изменения /i меняется на /J = —шц и переменнгш fi возра-

стает и трансверсально пересекает прямую /i = —1 (рис. 8.3). Таким

1 0

<р

] fi

Рис.

8.3

Рис.

8.4

образом, на прямых \fi\ ~ 1 возникает скользящий режим, что и га-

рантирует соблюдение ограничения \fi\< 1, быть может, с некоторого

момента времени.

Достоинство этого способа заключается в том, что управляемость

объекта не теряется при выходе на ограничение, так как при изме-

нении знака ^ переменная fi немедленно "сходит" с него, а это то,

что нужно. Заметим, что закон (8.3) можно записать в виде одной

формулы, если ввести функцию

^(p) = (l-|sat(M)|)/(l-H), (8.4)

(ее график дан на рис. 8.4) и бинарную операцию /?(у, О — v(/^)sgn ^.

8.1.

Ограничения

операторной

переменной

249

В новых обозначениях закон (8.3) эквивгигентен следующему, более

простому,закону:

ii = -k0{<p,i)-

(8.5)

Способ II. Заметим, что функцию

(р

из (8.4) можно представить

разностью

ip{^i)

sg{\-\-fi)-sg{^i-l), (8.6)

где sg(^) — функция знака (ее график приведен на рис. 8.5а). Тогда

sg(#)

(\+ц)

sg(i -И)

-1

б в

Рис.

8.5

в результате вычитания графиков на рис.

8.55и

8.5в получаем требу-

емый график рис. 8.4. После подстановки (8.6)

(8.5) получаем

/i =-A;sg (l4-/i)sgn^ +Asg (//-l)sgn^,

fc =

const

(8.7)

Учитывг1Я особенность знакового умножения, формулу (8.7) можно

регшизовать без бинарной операции путем использования двух кана-

лов распространения сигнала (рис. 8.6). Эта схема работает следу-

ющим образом. Если

^ >

О,

то

—sgn

^ =

—1

и из

двух диодов

Di,

Рис. 8.6

250

Глава 8. Ограничения, физические основы компенсации

Di пропускает сигнал только D^- Если при этом /i + 1 > О, то ключ

sw2 замкнут и /i = —к, что и требуется. Это происходит, пока ц не

достигнет значения /i =

—

когда sw2 размыкг^ется, и тогда /i =

—

пока ^ > О, либо пока ^ не сменит знак. В этом случае проводящим

становится D\, а не Dj. работает верхняя цепь, и если 1

—

/i > О, то

ключ swl замкнут и fi = к, как и должно быть. Как только станет

/i = 1, если только ^ не сменит знак, swl разомкнётся, фиксируя fi = 1.

Достоинство этой схемы в том, что в ней не возникает скользящего

режима на

|/j|

= 1.

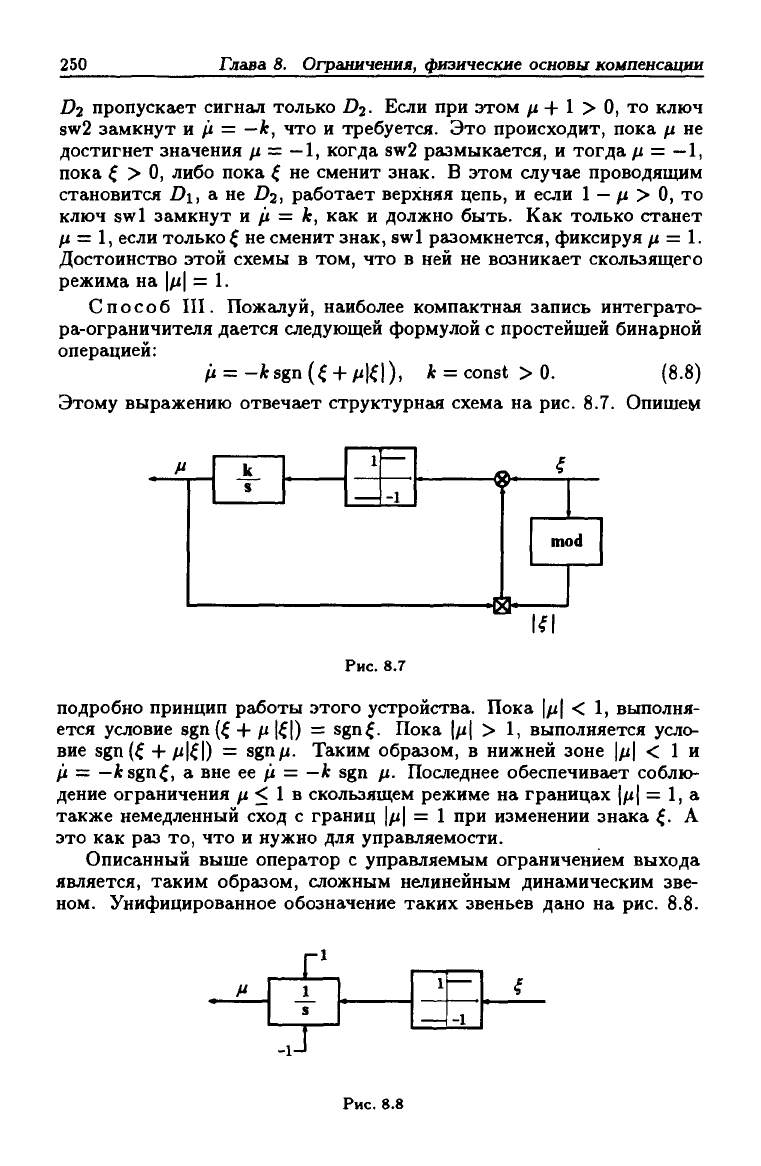
Способ III. Пожалуй, наиболее компактная запись интеграто-

ра-ограничителя дается следующей формулой с простейшей бинарной

операцией:

/i =-fcsgn(^-|-/i|^|),

= const>0. (8.8)

Этому выражению отвечает структурная схема на рис. 8.7. Опишем

-1

Рис.

8.7

ff. ^

'В

а.

я*

mod

1^1

подробно принцип работы этого устройства. Пока \/л\ < 1, выполня-

ется условие sgn

(^-I-/i

1^1) = sgn^. Пока |/i| > 1, выполняется усло-

вие sgn(^ -f fi\^\) = sgn/i. Таким образом, в нижней зоне |^i| < 1 и

fi = —ksgn^, а вне ее /i = —к sgn fi. Последнее обеспечивает соблю-

дение ограничения /i < 1 в скользящем режиме на границах |/х| = 1, а

также немедленный сход с границ \fi\ = 1 при изменении знака ^. А

это как раз то, что и нужно для управляемости.

Описанный выше оператор с управляемым ограничением выхода

является, таким образом, сложным нелинейным динамическим зве-

ном. Унифицированное обозначение таких звеньев дано на рис. 8.8.

-1

Рис. 8.8