Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

(6.20)

6.3.

Статическая операторная обратная

связь 221

6.3.5. Инерционно-релейная

координатно-операторная обратная связь

при неизвестном параметре при упрхшлении

В этом пункте для стабилизации Ре-объекта (6.8)

^ = 2(d-g/i)^ + b/i-|-a-g/i, b =

+ 2qd

аеА,

be В,

применяется инерционно-релейная КО-связь вида

qfi

—

b~fi = ksgn^, к = const > О,

b- =b- + 2qd,

которая может быть использована и тогда, когда значение параме-

тра 6 неизвестно. Отметим, что допускаются изменения неизвестных

параметров а, 6 во времени произвольным образом. Структура ре-

гулятора (6.20) совпадает со структурой регулятора на рис.6.8 при

замене 6 на 6~.

Подстановка (6.20) в (6.8) дает уравнение замкнутой системы в

следующем виде:

i = 2{d- qn)i + (6 - b-)ii -ksgni + a. (6.21)

Поскольку и в этом случае переменная ц равномерно ограничена (при

g < 0), то, очевидно, существует такое число а", что при fc > а° в

точке ^ =

возникает скользящий режим.

В скользящем режиме можно считать выполненными равенства

^ = 0, ^ = 0,

тогда из уравнения (6.21) эквивалентное значение разрывного сигнала

определяется в виде

^sgneq^ = a-|-(6-6")/j.

После подстановки этого значения в уравнение регулятора (6.20)

находим уравнение движения операторной переменной /i в скользящем

режиме

g/i-6/i = a, (6.22)

которое в точности совпадает с уравнением скольжения для перемен-

ной /* из предыдущего пункта. Поэтому верны все сделанные ранее

выводы и, в частности, о том, что уравнение скольжения по основной

переменной после окончания переходного процесса уравнения (6.22)

дается выражением

XI = -{d + qa/b)xi.

Следовательно,

• ив этом случае имеет место неустранимый (хотя и сколь угодно

малый при q

—>

—0) динамический статизм.

222 Глава 6. Теория

операторной обратной

связи

Сохраняются также все замечания и о прочности системы управления,

и о физическом смысле эффекта компенсации возмущений а, Ь.

Ход проекций фазовых траекторий на множество Gt в плоскости

{xi,X2) показан на рис. 6.5, а для получения структуры системы до-

статочно в схеме на рис. 6.11 заменить параметр 6 на 6~ и добавить

двойную стрелку J^ 6 € В, действующую на объект Р и отражающую

влияние фактора неопределенности.

Достоинство регулятора (6.20) состоит в том, что он эффективно

действует при любых неизвестных параметрах а^ А,Ь ^ В.

6.3.6. Интегрально-релейная

координатно-операторная обратная связь

Максимально возможное упрощение системы управления достигается

при использовании интегрально-релейного закона

g/i = Jk8gn^. (6.23)

В этом случае замкнутая система управления описывается (6.23) и

уравнением

^ = 2((f-?/i)^-|-6/i-»-a-Jtsgn^, b =

h-{-2qd.

(6.24)

При возникновении скользящего режима можно считать выполнен-

ными в надлежащем смысле равенства

а поэтому эквивалентное значение разрывного сигнала имеет следую-

щее значение:

После его подстановки в уравнение регулятора (6.23) находим точные

и асимптотические уравнения скольжения для переменных /i и zi в

виде известных уже из предыдущего выражений

qii-bn = a, xi = -{d-qn)xi- (d + qa/b) xf,

tioo=-a/b, xi = -{d+qa/b)xi.

Поэтому справедливы все выводы, сделанные в пунктах 6.3.4 и 6.3.5.

Единственная трудность в проведенном рассуждении состоит в

том, что факт возникновения скользящего режима в точке ( = О не

просто усмотреть из уравнений замкнутой системы (6.23), (6.24). По-

скольку нас интересует анализ в малом, то этот вопрос^можно иссле-

довать с помощью функции Ляпунова вида

« = (1/2)^ (6.25)

6.3. Статическая операторная обратная связь

223

Действительно, полагая для простоты, что параметры а,Ь = const,

после дифференцирования функции (6.25) в силу уравнений движения

(6.23),

(6.24) находим

(6.26)

v = i = ^[2(d- qn)i +

bfi

+ a- asgn^] =

= 2{d-qfi)e-\^\[d-(b(i + ^)4t^a

Далее заметим, что в положении равновесия

^ =

О,

1/1

+ 0 = 0,

поэтому в его окрестности в (6.26) доминирует член —d|^|. Следова-

тельно, существует число 7 >

такое, что

< -7lf

= -7\/2и = -7*>А.

Решая последнее дифференциальное неравенство, находим оценку

из которой следует, что в некоторой окрестности положения равнове-

сия скользящий режим всегда возникает через конечное время, что и

требовалось доказать.

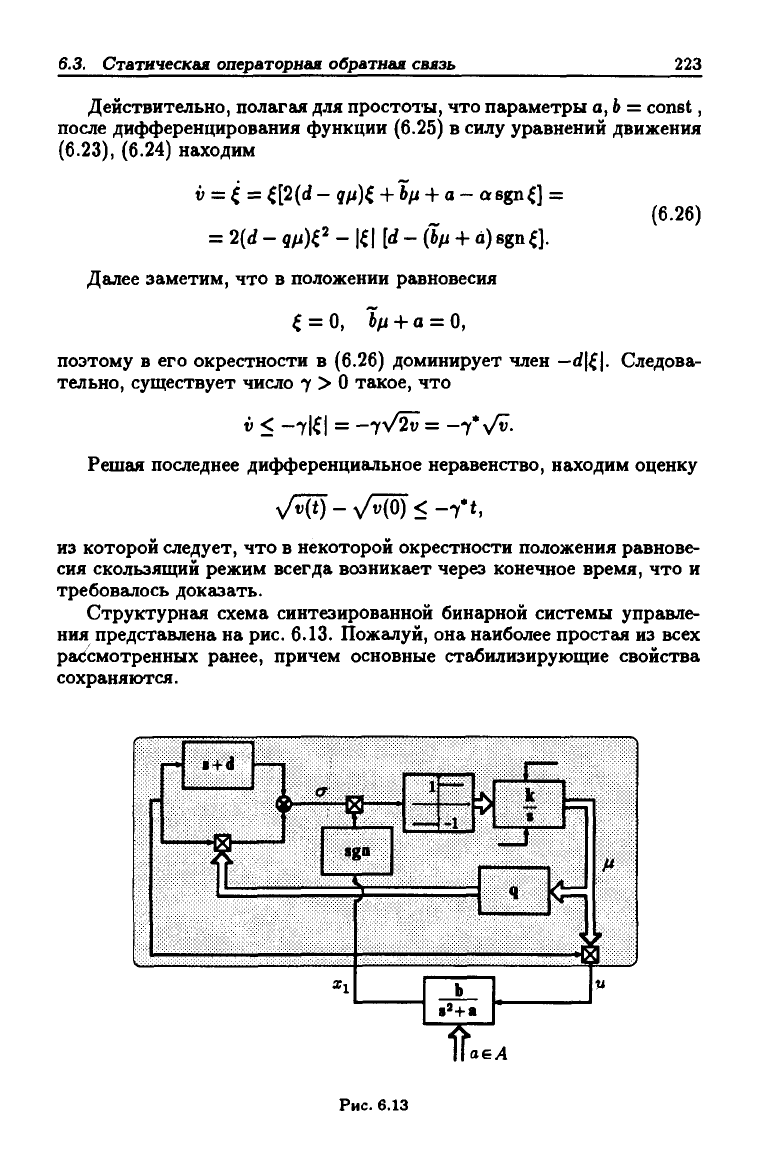
Структурная схема синтезированной бинарной системы управле-

ния представлена на рис. 6.13. Пожалуй, она наиболее простая из всех

рассмотренных ранее, причем основные стабилизирующие свойства

сохраняются.

•+d

X. <r „

sgn

—i^—

P-,—, г-

'-J

' -i

• -1

q (

[

Рис. 6.13

224 Глава 6. Теория

операторной обратной

связи

Проведенное исследование показало, что с помощью 0-связи можно

значительно повысить качество переходных процессов бинарной си-

стемы управления, в частности:

• устранить колебательность фазового вектора в множестве Gs;

• повысить прочность системы управления путем уменьшения ко-

эффициентов передачи в главном канале и, более того, вовсе отка-

заться от использования в КО-законах демпфирующей компоненты

= -Ы;

• понизить размерность замкнутой системы на 2 порядка, напри-

мер с 3-го до 1-го (при сочетании с динамической разрывной КО-

связью);

• сколь угодно точно достигнуть (правда, в ущерб прочности) тре-

буемого качества переходных процессов.

При этом статическую 0-связь неизбежно сопровождает статизм (ди-

намический статизм в основных переменных), что, впрочем, есте-

ственно для любой статической обратной связи. Вопрос об исполь-

зовании динамической 0-связи здесь не затрагивается. В следующей

главе используем ОК-связь для устранения указанного статизма.

Глава 7

Теория операторно-координатной

обратной связи

Данная глава посвящена качественному исследованию бинарных си-

стем автоматического управления с разными типами обратной связи.

Потенциально подобные нелинейные динамические системы стабили-

зации должны обладать самыми совершенными свойствами, близкими

к тем идеальным, которые можно наблюдать у систем управления с

глубокой обратной связью. Однако, в отличие от последних, бинарная

система стабилизации прочна в классе регулярных и сингулярных воз-

мущений. Пожалуй, эта глава в наиболее полной степени демонстри-

рует использование эффекта нелинейности в задачах стабилизации су-

щественно неопределенного объекта. Итоговые уравнения движения

системы стабилизации принципиально нелинейны, достаточно сложны

и обладают глобально устойчивыми решениями, которые мало зависят

(а в некоторых случаях не зависят) от факторов неопределенности и

могут быть описаны простейшими дифференциальными уравнениями.

Подобные нелинейные уравнения есть прямой результат применения

разработанной в монографии теории.-

О возможности получения подобных уравнений другими методами

сегодня ничего неизвестно.

7.1.

Динамический статизм

и операторно-координатная обратная связь

В предыдущих главах было установлено, что стабилизация в нуле не-

определенного объекта

XI = Х2,

Х2 = axi +bu, а

А, b Е В,

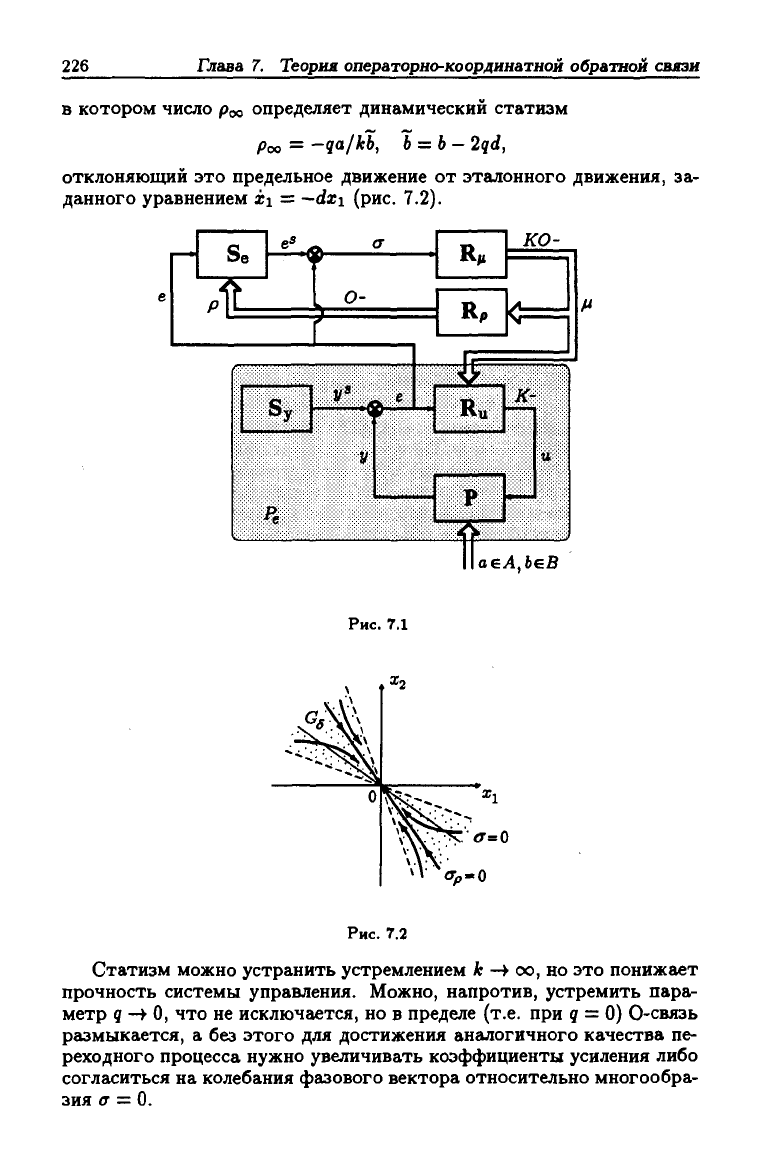
с помощью трех типов обратной связи (рис. 7.1), достигается при лю-

бых, в том числе и переменных, параметрах объекта а Е А, b € В.

При этом в множестве

Gs = {x\ \(T\<S\xi\}

предельное движение описывается уравнением

XI = -(d + poo)xi,

226

Глава 7. Теория операторно-координатной обратной связи

котором число

роо

определяет динамический статизм

Роо

= -qa/kb,

= 6- 2qd,

отклоняющий это предельное движение от эталонного движения, за-

данного уравнением xi = ~dxi (рис. 7.2).

аеА,ЬеВ

Рис. 7.1

Рис. 7.2

Статизм можно устранить устремлением

Аг

-> оо, но это понижает

прочность системы управления. Можно, напротив, устремить пара-

метр ? ->

О,

что не исключается, но в пределе (т.е. при g = 0) 0-связь

размыкается, а без этого для достижения аналогичного качества пе-

реходного процесса нужно увеличивать коэффициенты усиления либо

согласиться на колебания фазового вектора относительно многообра-

зия

<т

= 0.

7.1.

Динамический статиэм

227

Стоит отметить, что устремление параметра 5 -> О, как это сле-

дует, например, из уравнения интегрально-релейного КО-регулятора

fi=-8gn ^,

означает, по существу, введение глубокой обратной связи в КО-конту-

ре регулирования, так как при этом k/q -¥ оо. Это, как известно,

ведет к потере прочности и, хотя значения скрытых параметров в

регуляторе можно считать меньшими, нежели значения скрытых па-

раметров в объекте, и, следовательно, критическое значение коэффи-

циента усиления этого контура, при превышении которого требуется

устойчивость, выше, тем не менее в принципиальном плане следует

поискать новые средства для точного решения рассматривг^мой за-

дачи стабилизации.

Важно также отметить, что в системах со статической 0-связью и

разрывной КО-связью при возникновении скользящего режима упра-

вление в главном контуре описывается выражением и = (k/q)

(т,

хотя, быть может, k/q >

ксг,

неустойчивость не наступает. Обосно-

вание этого факта почти очевидно и здесь не приводится.

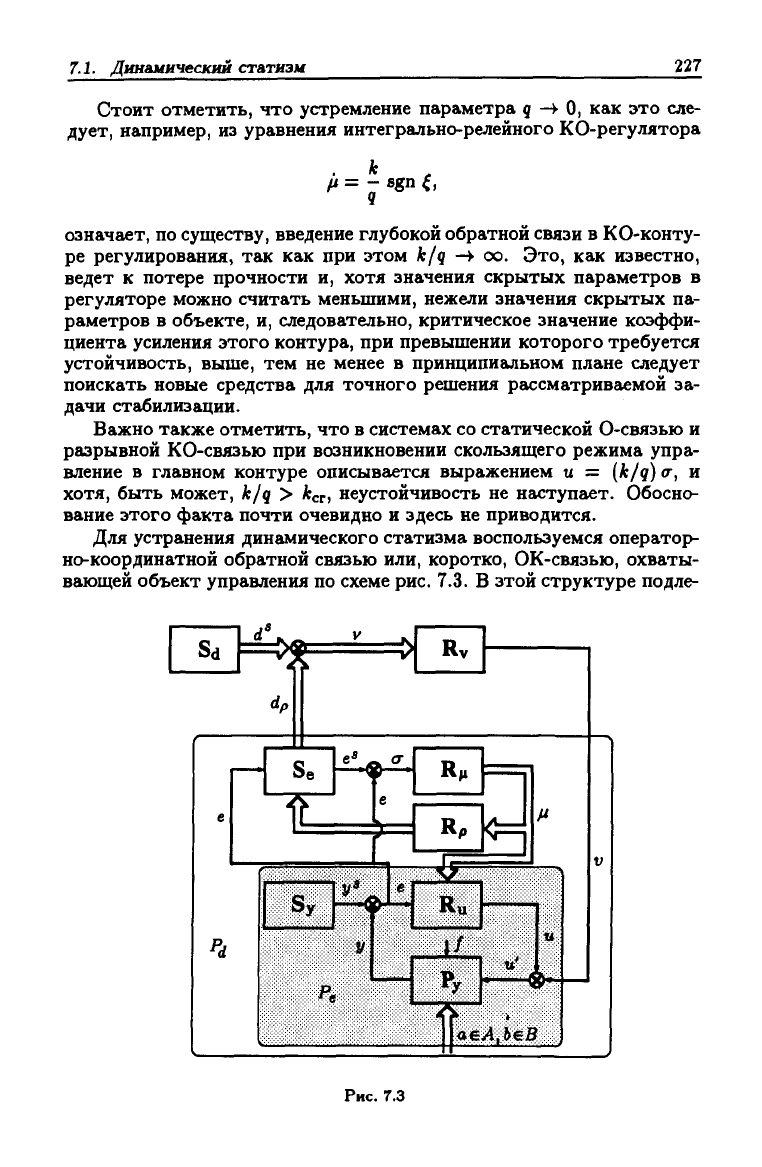
Для устранения динамического статизма воспользуемся оператор-

но-координатной обратной связью или, коротко, ОК-связью, охваты-

вающей объект управления по схеме рис. 7.3. В этой структуре подле-

_ (

\ " > Rv

5е

И-^-Ч RM 1==Т1

jH "Р Ч|—

1 , |^= =Ц

У*

Sy '""V

Р^

и'

1 Pjr ——® 1

[аеЛ.беВ

Рис. 7.3

228

Глава 7. Теория операторно-координатной обратной связи

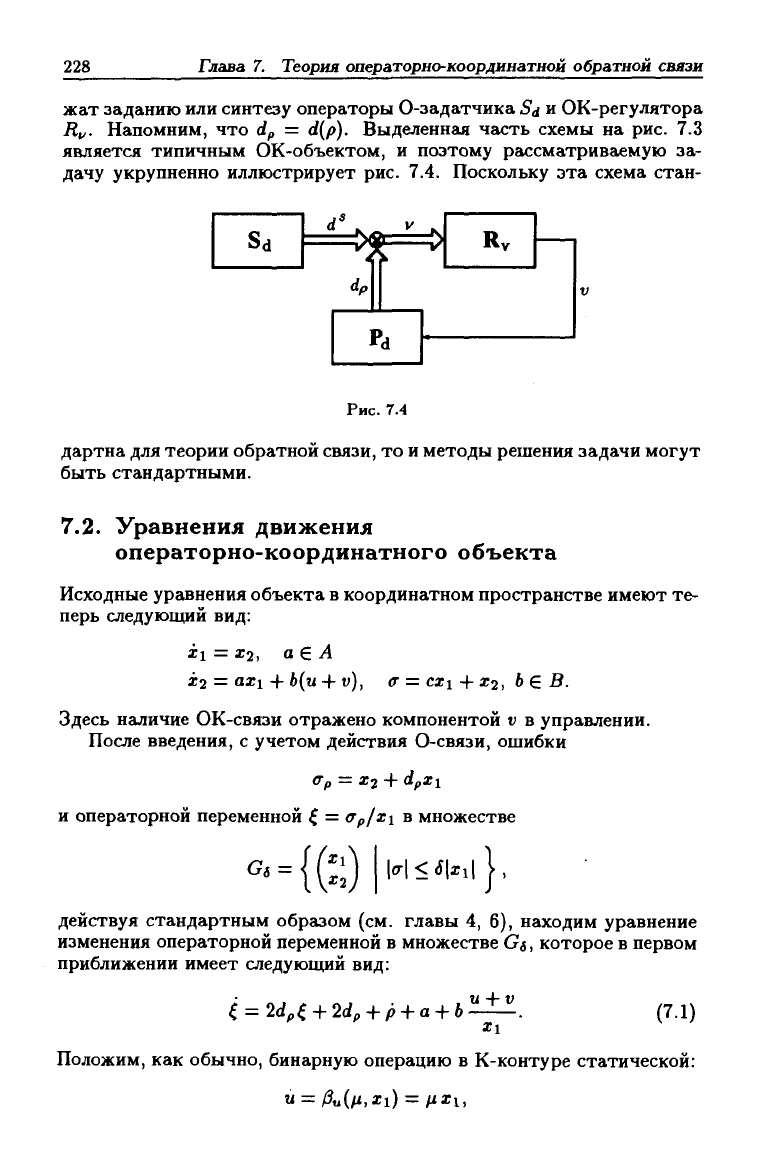
жат заданию или синтезу операторы 0-задатчика Sd и ОК-регулятора

Rf,. Напомним, что dp = d{p). Выделенная часть схемы на рис. 7.3

является типичным ОК-объектом, и поэтому рассматриваемую за-

дачу укрупненно иллюстрирует рис. 7.4. Поскольку эта схема стан-

с>5е=Ф

Рис.

7.4

дартна для теории обратной связи, то и методы решения задачи могут

быть стандартными.

7.2. Уравнения движения

операторно-координатного объекта

Исходные уравнения объекта в координатном пространстве имеют те-

перь следующий вид:

XI = Х2, ае А

Х2 = axi + b{u + v),

(т

= сх\ +

Х2,

b £ В.

Здесь наличие ОК-связи отражено компонентой v в управлении.

После введения, с учетом действия 0-связи, ошибки

(Гр

= Х2 + dpXi

и операторной переменной ^ =

<Тр1х\

в множестве

действуя стандартным образом (см. главы 4, 6), находим уравнение

изменения операторной переменной в множестве d, которое в первом

приближении имеет следующий вид:

^ = 2dp^ + 2dp + p + a + b

и +

Хх

(7.1)

Положим, как обычно, бинарную операцию в К-контуре статической:

и = P^{fx,xi) = fixi,

7.3.

Статический ОК-регулятор

229

аналогично распорядимся выбором бинарной операции в ОК-контуре:

где,

как принято выше, /х и

»/

— операторные переменные. При таком

выборе уравнение (7.1) принимг1ет следующий вид:

i = 2df^ + 2dp + p + a +

b(fi

r)),

(7.2)

где ц и

Г)

можно рг1ссматривать в качестве управлений.

Сохраняя преемственность, положим 0-связь статической:

р =

—qfi,

q = const,

а воздействие на параметр 5е-задатчика — адаптивным:

dp = d + р.

Тогда при интегрально-релейном КО-регуляторе

qfi = kisgn^, Ari = const,

уравнение изменения операторной ошибки ^ (7.2) примет вид

i = 2{d-q(i)^ + bii-kisgn^ + a +

bT},

b =

b-2qd.

(7.3)

Уравнение (7.3), дополненное уравнением изменения основной пе-

ременной

ii = -{d + p)xi+^xi, (7.4)

и уравнение ОК-регулятора

т]

= R^y, (7.5)

где ОК-ошибка регулирования

i/ = df,-d = p, (7.6)

я R,, — оператор ОК-регулятора, описывают в множестве Gg замкну-

тую систему регулирования с четырьмя типами обратной связи. По-

скольку

= ^=-*isgn^, (7.7)

то нужно позаботиться о надлежащем выборе оператора Д,,, гаран-

тирующего стабилизацию ошибки i/ в нуле. Ргьссмотрим некоторые

варианты.

7.3.

Статический ОК-регулятор

Пусть оператор R,j в (7.5) является простейшим линейным операто-

ром, т.е.

т]

= k^v- Тогда надлежит исследовать на устойчивость следу-

ющую систему уравнений, для удобства обозначаемую символом Е*^:

i = 2(d- qn)i + bn-ki sgn^ -|- kibu + a, (7.8)

i> = -*isgn^. (7.9)

230 Глава 7. Теория

операторно-координатной обратной

связи

Поскольку и = р, р= —9А«, то после введения обозначения

6* = (1 - 9*2)6 - 2qd,

эту систему можно переписать в более удобном виде

^ = 2(d - qfi)^ + ЬУ - ki sgn^ + а,

i>= -kisgn^.

Уравнения, подобные уравнению (7.8) Е'-системы, подробно иссле-

довались в главах 4, б, поэтому можно утверждать, что при выполне-

нии неравенства fci > а° в точке ^ =

возникает скользящий режим.

Поскольку при этом, кроме того, в определенном смысле ^ = О, то

эквивалентное значение разрывного сигнала определяется следующим

выражением:

*isgneq^ = 6*/i + a.

После подстановки этого выражения в уравнение (7.9) Е'^-системы

находим уравнение изменения 0-ошибки i/ в виде

—b*fi —

a. В силу

того,

что и = р=

—qf^,

окончательно имеем уравнение для ошибки i/:

й = —и-а. <7.10)

Поскольку b*/q < О, то уравнение (7.10) асимптотически устойчиво и

имеет положение равновесия в точке

j/<«

= |^, b' = (l-qk2)b-2qd.

Следовательно,

• статическая ОК-связь не устраняет динамический статизм, а лишь

несколько уменьшает его величину по сравнению с рассмотрен-

ными выше системами управления.

Действительно, например, в системе со статической 0-связью вели-

чина статизма давалась выражением

Роо

= qa/b, 6 =

6 —

2qd,

но так как 6* > 6, то очевидно имеем требуемое

I/QO

Роо •

Увеличением ^2

—>

оо можно устранить статизм

I/QO,

НО

при этом

будет нанесен ущерб прочности системы. Действительно, в этом слу-

чае вторая компонента управления линейно связана с основным упра^

влением

V = r]Xi = k2i^xi = —qk-iliXi = —qki^

и полное управление и' = и

-\-

v также пропорционгшьно основному

управлению

u' = {\-qk2)u. (7.11)