Емельянов С.В. Новые типы обратной связи
Подождите немного. Документ загружается.


7.4. Интегральный ОК-регулятор
231
Последнее
как раз и
означает, что действие статического ОК-регу-
лятора эквивалентно увеличению
в
(1
—
9^2)
раз
коэффициентов пе-
редачи КО-регулятора, что,
как
отмечалось ранее, понижает проч-
ность системы управления. Формула (7.11) также проясняет эффект
от использования статического ОК-регулятора. Описанную систему
900
1
Рис. 7.5
иллюстрирует рис. 7.5,
на
котором показан ход проекций фазовых
траекторий системы
на
множестве Gg после возникновения скользя-
щего режима.
7.4. Интегральный ОК-регулятор
Из классической теории регулирования известно, что статизм устра-
няется применением интегральной обратной связи, поэтому рассмо-
трим ОК-регулятор следующего вида:
Г)
=
—k2U,
^2
=
const. (7.12)
Уравнение (7.12) вместе
с
уравнениями КО-
и
0-регуляторов
qfi
= ki
sgn^,
ki =
const,
(713)
p=-qn,
9
=
const, (7.14)
уравнениями бинарных элементов
и'=
u-\-v
=:
цх1-\-Г1Х1
=
{ц
+
г))х1,
(7.15)
а также уравнениями движения объекта
в
КО-пространстве (xi,^)
xi = -{d-{-p)xi+^xi,
(7.16)
i
=
2(d + p)(,
+
bn + 2dp-irp +
br)
+ a,
а
G Л, 6
€ 5,
(7.17)
задает поведение замкнутой системы управления
с
четырьмя типами
обратной связи
на
множестве
Gs.

232
Глава 7. Теория
операторно-координатной обратной
связи
Как и ранее, полагаем
v = dp
—
d = p,
^xi = a, а
=:
xi + dxi,
= xi + d+pxi.
(7.18)
(7.19)
Структурная схема исследуемой бинарной системы приведена на
рис.
7.6. (выделен синтезированный нелинейный динамический ре-
гулятор второго порядка, полный порядок замкнутой системы ра-
г—
S + 0 1
1
ня 1
1Г
о- ,
р 1—1
у
• S + C 1
л
9
?п
^
•
1 , 1~ . •'»
М—J-1 ч*
_п /^
-ч
ч,
^1 Ь
к.
- ок-
S
КО-
и
=¥^=i
и'
Мое
л,
ЬеВ
Рис. 7.6
вен четырем). Задача теперь состоит в таком выборе параметров
системы, при котором гарантируется стабилизация переменной х\ в
нуле при асимптотически исчезающей зависимости переходного про-
цесса от неопределенных (для простоты — постоянных) параметров
а е Л, 6 е В.
Для анализа поведения синтезированной бинарной системы обра-
тимся к уравнениям изменения операторных переменных (^, /i, rj).
После подстановки соотношений (7.17), (7.14) в (7.12) и (7.13), (7.14) в
(7.17) получим в итоге совокупность дифференцигшьных уравнений,
описывающих так нгкзываемую Е^-систему:
i = 2{d-
qy.)(,
-I-
6/i - fci sgn ^ +
Ь»7
-I-
а, 6 = 6- 2qd,
qii = kisgn(„
•q
=
qk2H.
(7.20)
Довольно ясно, что положение равновесия Е;-системы находится в
точке (^оо./^оо,»?»)) =
(О,
О,-а/6).

7.4. Интегральный ОК-регулятор 233
Убедимся, что в малой окрестности положения равновесия за ко-
нечное время в точке £ =
О
возникает скользящий режим. Для этого
достаточно умножить почленно первое уравнение Ef-системы на £ и
получить выражение
^i = -h\^\ + 2(d- qti)e + bfii + brji + ai,
из анализа которого прямо следует, что при выполнении условия
кг
>а°
существуют такие константы а, /? > О, что в окрестности
выполнено неравенство
которое эквивалентно дифференциальному неравенству
^ < -asgn£.
Из приведенных неравенств следуют утверждение о возникновении
скользящего режима в точке £ =
О
за конечное время и сходимость в
Gi к нулю основной переменной xi, так как из (7.16) имеем уравнение
XI = -(d + р)х1.
Однако этого мало, поэтому продолжим исследование.
В скользящем режиме, как обычно, из равенств £ = £ =
О
опреде-
ляем эквивгшентное значение разрывного сигнала в виде
^isgneq£ = b/i + b»?+a.
После подстановки найденного эквивалентного управления в уравне-
ния (7.20) Е^-системы получаем следующую совокупность дифферен-
циальных уравнений Е^-системы:
Положение равновесия Е^-системы находится в точке (О,
—а/Ь),
которая, естественно, совпадает с точкой (//со
>
'Поо)-
Устойчивость по-
ложения равновесия определяется асимптотическими свойствами ди-
намической системы
fi.= 'Ц+ -t),
T)
=
qk2H-
(7.22)
Ч Ч
234
Глава 7. Теория
операторно-коордииатной обратной
связи
Система (7.22) асимптотически устойчива тогда и только тогда,
когда гурвицев ее характеристический полином
<p{s)
= det {sE -А) = det
s - Ь/q -b/q
-qk2 s
= s^ s + kib.
Последнее имеет место при выполнении неравенств b/q < О, Лз > 0.
Заметим, что степень устойчивости системы (7.22) увеличивгьется при
q
—¥
О, т.е. назнач£1ется по произволу без изменения коэффициентов
передачи главного К-контура регулирования. Кроме того, из (7.14)
и (7.18) следует равенство v = —qn, и поэтому j/
—>
О, когда /i
—^
0.
Таким образом, интегральный ОК-регулятор решает поставленную
задачу об асимптотическом устранении с произвольным темпом ди-
намического статизма.
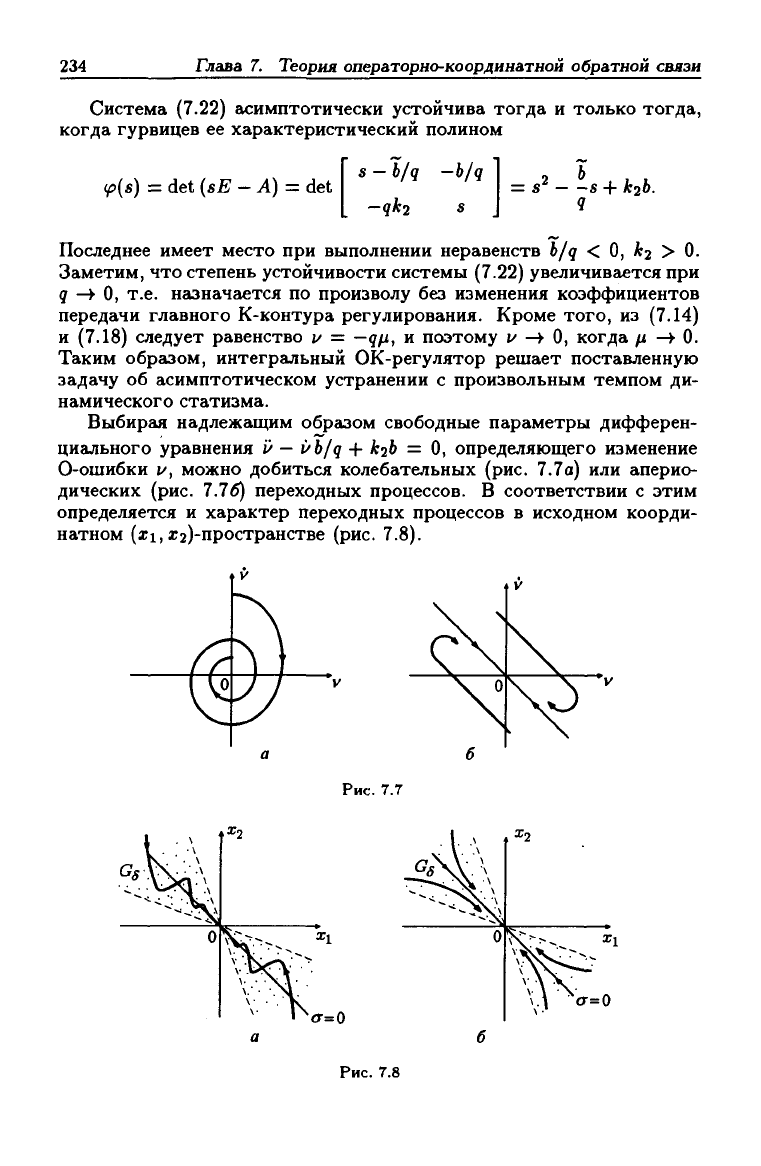
Выбирая надлежащим образом свободные параметры дифферен-
циального уравнения i/
—
и b/q + k2b = О, определяющего изменение
0-ошибки 1/, можно добиться колебательных (рис. 7.7а) или аперио-
дических (рис. 7.76) переходных процессов. В соответствии с этим
определяется и характер переходных процессов в исходном коорди-
натном (а;1,а;2)-пространстве (рис. 7.8).
Рис. 7.7

7.5. Основные
свойства
и
особенности
бинарных
систем
235
7.5.
Основные свойства и особенности
бинарных систем стабилизации
с различными типами обратной связи
Перечислим основные свойства и особенности бинарных систем ста-
билизации с различными типами обратной связи.
Отличие от идентификационного подхода. В рассмо-
тренной бинарной системе нет даже косвенного эффекта идентифи-
кации. Отсутствие идентификации следует из формулы
и принципиально отличг1ет предложенную схему управления от адап-
тивного подхода.
Эффект, лежащий в основе компенсации неопреде-
ленности. По формуле (7.15) сигнал управления
-Н)'
и' =:u + v = (fi-hrj)xi= 11 +
-\цх1.
(7.23)
с другой стороны, в скользящем режиме ^ = О, что эквивалентно по
формуле (7.19) равенству
<Гр
= х1 + dxi + pxi = 0. (7.24)
Но ^ = —qfi (см. (7.14)), и поэтому из (7.24) получаем следующее
соотношение:
XI + dxi <т
fiXi = = -.
Я Ч
Подставляя последнее соотношение в (7.23), находим
"-(-д)?-
По доказанному выше,
»7
-> т/оо = -а/Ь, /i -> О,
а значит и отношение т;//*
—>
оо. Иными словами,
• интегральный ОК-регулятор обеспечивает эффект неограничен-
ного нарастания коэффициента воздействия по ошибке регулиро-
вания
(Т
= ii
-I-
dx\, т.е.
(-^)^
-> 00, t -> 00.
Последнее полностью проясняет эффект компенсации факторов не-
определенности в привычных для теории регулирования терминах.

236 Глава 7. Теория операторно-координатной обратной связи
О прочности бинарной системы. Синтезированная бинар-
ная система (в силу использования конечных коэффициентов пере-
дачи) прочна, так как динамические или функциональные неидеаль-
ности приводят лишь к отклонению переменной ^ от нуля, т.е. |^| < Д,
Д = const < S. Последнее, очевидно, не нарушает асимптотических
свойств системы в исходных переменных (хг.хг)-
О стабилизации объекта с переменными параметра-
ми.
Изменение во времени параметра Ь ^ В принципиально не ме-
няет описанной выше картины, так как уравнения движения при этом
остаются прежними. Следует, однако, отметить, что при доказатель-
ствах устойчивости предпочтительнее использовать второй метод Ля-
пунова, а не операторные методы и преобразование Лапласа, как ра-
нее.
Если же меняется параметр а £ А, то все уравнения движения
также сохраняются, однако меняется их асимптотика.
Так, например, Ef-система (7.21)
qft = bfi +
Ьт]
+ а,
т)
= qhfJt
из асимптотически устойчивой превращается в диссипативную, т.е.
за конечное время ее решение погружается в инвариантный шар
/^•^ +
(Ьт)
-f- а)^ < const.
Поскольку I/ = р = —qfi, отсюда следует диссипативность и по i/, т.е.
|f I < const. Это означает, что устранение динамического статизма не
гарантируется. Но этого и следовало ожидать, так как интегральный
закон аннулирует только постоянные возмущения, для аннулирования
произвольного волнового возмущения Ка = О, как известно, в регуля-
торе следует применять оператор К~^ — обратный к аннулирующему
оператору К.
О порядке замкнутой системы управления. Из струк-
турной схемы замкнутой системы, приведенной на рис. 7.6, видно,
что исходный порядок системы равен четырем. После возникнове-
ния скользящего режима в 0-регуляторе он понижается на единицу и
описывается следующими уравнениями:
qii = bfi +
btj
+ a,
Ti
= qk2fi
ii = -{d-qfi)xi.
Если степень устойчивости Е^-системы установить много больше чи-
сла d, а это всегда возможно выбором параметров регулятора, то ее
движения можно считать быстрыми по отношению к основному дви-
жению
XI = -dxi (7.25)

7.6. Разрывная ОК-связь
237
и, следовательно, фактически порядок замкнутой системы равен еди-
нице. Иными словами, сложная неопределенная нелинейная система в
итоге ведет себя как скалярная система (7.25).
Подчеркнем, однако, что это драматическое понижение порядка
справедливо только в асимптотике. Если же принять разрывную ОК-
связь, то того же эффекта можно добиться финитно, т.е. за конечное
время.
7.6. Разрывная ОК-связь
Из предыдущего рассмотрения ясно, что интегральный ОК-регуля-
тор устраняет динамический статизм лишь в асимптотике и не га-
рантирует этого при переменных параметрах а £ А,
Ь
£ В. Поэтому
рг1ссматриваемая в данном пункте задача такова:
• предложить эффективные методы финитного устранения динами-
ческого статизма, работоспособные и при переменных параметрах
объекта.
Из классической теории регулирования известно, что при отсут-
ствии информации о характере изменения возмущения для этой цели
могут применяться: большой коэффициент усиления, разрывная (ре-
лейная или СПС) обратная связь.
Увеличение коэффициента усиления понижает прочность системы
управления, поэтому исследуем возможности разрывной ОК-обратной
связи при решении сформулированной задачи.
7.6.1.
Интегрально-релейный ОК-регулятор
В этом случае уравнение ОК-регулятора имеет вид
т] —
—ki sgn
I/,
(7.26)
чему соответствует структурная схема на рис. 7.9, проясняющая на-
sgn
Рис. 7.9
звание регулятора. Уравнение (7.26) вместе с уравнением изменения
0-переменной ^
^ = 2<fp^
-I-
6/i - Ai sgn^
-(-
6г7
-I-
а
и уравнением КО-регулятора
(7.27)
(7.28)
238
Глава
7.
Теория операторно-координатиои обратной
связи
определяют, с учетом равенства
I/ = -gfi, (7.29)
исследуемую замкнутую систему дифференциальных уравнений. Если
уравнения (7.2б)-(7.29) дополнить уравнением изменения основной пе-
ременной
xi = -{d + p)xi+ixi, (7.30)
в котором использованы переменные
^Xi = (Т,
<Т
= Xi + dXi, <Тр=:
<Т
+pXi = Xi+dpXl,
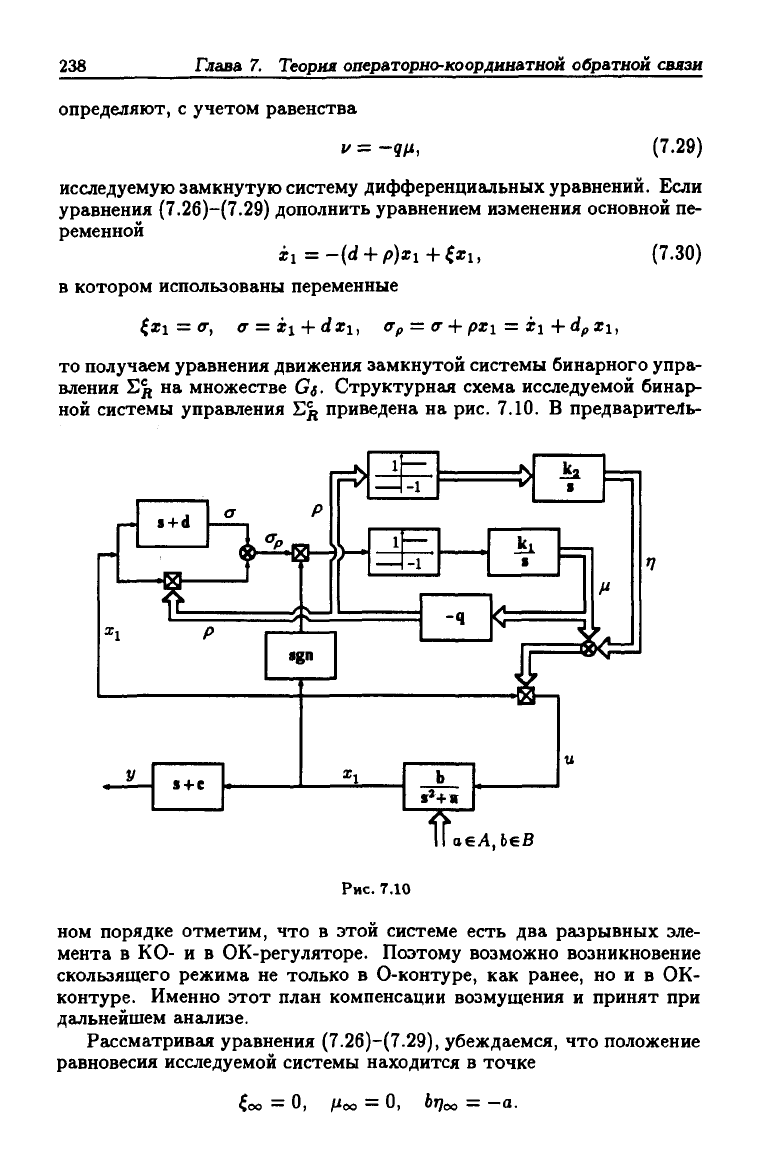
то получаем уравнения движения замкнутой системы бинарного упра-
вления Ед на множестве Gs- Структурная схема исследуемой бинарь
ной системы управления Ед приведена на рис. 7.10. В предваритеЛь-
s + d
ГР>:^?
•Я—
_}^Тгг
» + с
sgn
-1
-q
**+»
1
aeA.bsB
£
*<Й
Рис. 7.10
ном порядке отметим, что в этой системе есть два разрывных эле-
мента в КО- и в ОК-регуляторе. Поэтому возможно возникновение
скользящего режима не только в 0-контуре, как ранее, но и в ОК-
контуре. Именно этот план компенсации возмущения и принят при
дальнейшем анализе.
Рассматривая уравнения (7.2б)-(7.29), убеждаемся, что положение
равновесия исследуемой системы находится в точке
^оо
=0,
fiao
= о,
Ьг)оо
= -а.

7.6. Разрывная ОК-связь 239
Поэтому, анализируя уравнение
i = 2dp^+
Ь(л
- ki 8gn ^ +
Ьт]
+ а, b =
b-2qd,
(7.31)
убеждаемся, как и во всех аналогичных случаях ранее, что при выпол-
нении условия fci > а" в точке ^ =
О
существует скользящий режим со
следующим эквивалентным значением разрывного сигнала:
*'isgneq^ = b/i-|-6r; + a.
После подстановки найденного эквивалентного значения в уравне-
ние КО-регулятора (7.28) получаем 2д-систему уравнений, подлежа-
щую дальнейшему анализу:
ri
= -k2agnfi.
Для анализа этой Ед-системы удобно положить 6 = const и сделать
замену переменного по формуле
е
=
Ьт)
+ а,
тогда ее уравнения движения примут вид
g/i = 6/i-|-e,
ё = -k2Sgnfi + a,
и положение равновесия переместится
в
нуль:
(/i
=
0,e
=
0).
Если предположить, что
ЛгЬ > sup |d|,
t>o
то качественные поведения Ед-системы и системы, описываемой урав-
нениями
9A = 6/i +
e,
(7 33)
ё = —k2bsgnfi,
совпадают, поэтому далее имеем дело с более простыми уравнениями
(7.33),
считая впредь, что они и задают Ед-систему.
Напомним, что Ед — релейная система. Подобные системы уже
подробно рассматривались нами ранее, поэтому просто воспользуемся
результатами проведенного анализа в первой части монографии (см.
главу 2). В результате сшивания по оси /i =
О
фазовых траекторий,
отвечающих решениям систем
qfi = bfi + e, с = -k2b,
qfi = bfi + e, ё = +k2b,

240
Глава 7. Теория
операторио-координатнои
обратной связи
получг1ем фазовый портрет £д-системы (рис. 7.11). Из рис. 7.Не
видна тенденция "скручиваемости" траекторий к нулю. Для ана-
лиза асимптотики этого движения воспользуемся вторым методом
Рис. 7.11
Ляпунова. Заметим, что достаточно доказать факт /л
—>
О, так как
и
—
—qfi, а, следовательно, одновременно i/
—^
0.
Возьмем пробную функцию
v=\n\-\-
2k2bq'
ее производнс1я в силу Ед-системы (7.33) имеет вид
е . f
Ъ
е\ е
v = nsgn ti-if т-те =
-/i-f-
- I sgn^i sgn/i =
«2P \q q J q
Поскольку
|/j|
= f
—
e^/2k2bq, то последовательно имеем
н
V :=
—
V —
q 2k2bq^
е < -V.
~ q
Из этого неравенства следует экспоненциальная оценка
v{t) < i;(0) exp j -t .
Напомним, что g < О, и, следовательно,
• интегрально-релейный ОК-регулятор способен компенсировать не-
известное и переменное возмущения а € Л, но делает это только
асимптотически.
Для достижения финитной компенсации требуются более "хитрые"
регуляторы.
