Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

8.4. О компенсации координатного возмущения

261

шар вырождается в точку О, как это и должно быть. Шар диссипатив-

ности jBr(O) можно уменьшить, а значит, поднять точность стабилиза-

ции, введением надлежащих О- и ОК-связей. Подробное обоснование

этого утверждения здесь не приводится.

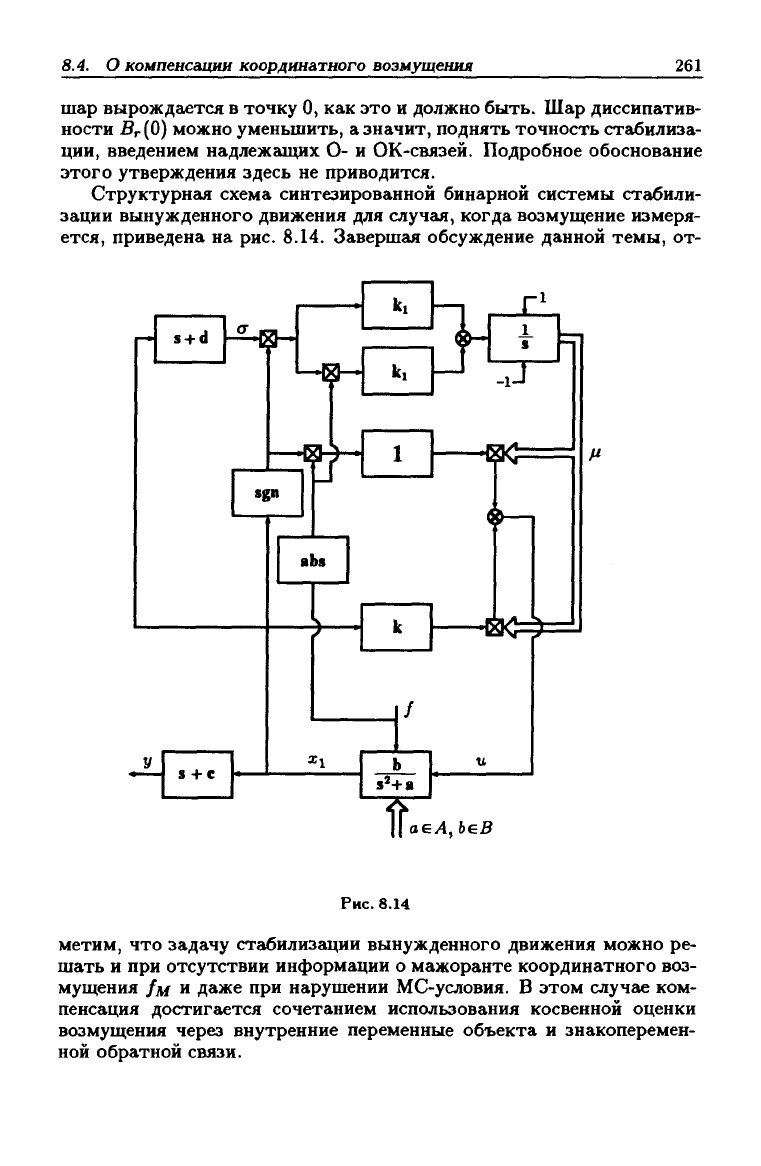
Структурная схема синтезированной бинарной системы стгкбили-

зации вынужденного движения для случая, когда возмущение измеря-

ется, приведена на рис. 8.14. Завершг1я обсуждение данной темы, от-

,—, 1—1 "' h

L^5^ ki 1

-1

1—|яЛ-|

1 1

1?'<==|

sgn

(

abs

ч 1- •!

*п

J '• -laivr-

^\ Ь ^

s*+«

оеЛ,

6eJ3

Рис. 8.14

метим, что задачу стабилизации вынужденного движения можно ре-

шать и при отсутствии информации о мажоранте координатного воз-

мущения ftf и даже при нарушении МС-условия. В этом случае ком-

пенсация достигается сочетанием использования косвенной оценки

возмущения через внутренние переменные объекта и знакоперемен-

ной обратной связи.

Глава 9

Дифференцирование сигналов

Под дифференцированием в теории управления обычно понимается

обработка сигнала с целью получения оценок его производных. Основ-

ными препятствиями на пути идеального дифференцирования явля-

ются физическая неосуществимость идеального дифференциатора и

неустранимое противоречие между точностью операции дифференци-

рования и операцией фильтрации помех. Теория дифференцирования

является разделом общей теории фильтрации, однако имеет весьма

существенную особенность, которая состоит в отсутствии модели об-

рабатываемого сигнала или точной информации о ее параметрах, что

характерно для теории фильтрации. Поэтому дифференцирование до

сих пор является одной из наиболее трудных задач теории управления.

Априорная неопределенность в постановке задачи дифференцирова-

ния предопределяет поиск наиболее совершенных дифференциаторов

в классе нелинейных динамических систем.

Цель настоящей главы состоит в демонстрации возможностей но-

вых видов нелинейных обратных связей в задаче дифференцирования.

9.1.

Постановка задачи дифференцирования

При решении многих задач естествознания часто требуется распола-

гать оценками производных функций. Далее для удобства, предпо-

ложим, что эти функции являются функциями времени, и будем по

традиции называть их сигналами.

Проблема дифференцирования возникает и в теории.управления

в связи, например, с восстановлением по выходу системы ее полного

фазового вектора. В тех случаях, когда эта проблема разрешима, с по-

мощью преобразования переменных можно получить фазовый вектор

в произвольных координатах. Задача дифференцирования сигнала

относится к числу некорректно поставленных задач, и это связано, в

частности, с тем, что из равенства

вовсе не следует, что

9i(t)=Mt}

(91)

dgdt) _ dg2(t)

9.1.

Постановка

задачи

дифференцирования

263

Более того, указанные производные могут даже не существовать.

Поэтому прежде всего следует позаботиться о такой предварительной

обработке сигнала, когда естественное следствие (9.1)-+(9.2) имеет

место. Это достигается использованием фильтра Fin предваритель-

ной обработки сигнала (рис 9.1) и его преобразованием в гладкий

сигнал д. Задача дифференцирования некорректно поставлена еще и

Рис. 9.1

потому, что результат дифференцирования двух сколь угодно близ-

ких сигналов может отличаться на произвольную величину.

Действительно, рассмотрим два сигнала

дп (t)

= с = const, g2{t) = gi{t) + esmwt,

(9.3)

где e — сколь угодно малая константа, w — частота помехи (рис. 9.2).

Дифференцируя функции из (9.3), имеем д\ = О,

flf2

ewcoswf.

Гра-

фики производных даны на рис. 9.3. Видно, что опшбка дифференци-

рования

может превзойти любое наперед заданное число. Поэтому о "чи-

стом"

дифференцировании говорить не приходится, можно вести речь

только об оценках производной д, измеряя ее близость к истинной

производной в той или иной метрике. Часто удобно различать в

hit)

Я^Л)

5ШШК

2е

Рис. 9.2

Рис. 9.3

264

Глава 9. Дифференцирование сигналов

структуре дифференциатора часть, которая отвечает за собственно

дифференцирование сигнала, от части, предназначенной для форми-

рования оценки производной. Последняя операция реализуется с по-

мощью некоторого фильтра Fouti и указанное разделение функций ил-

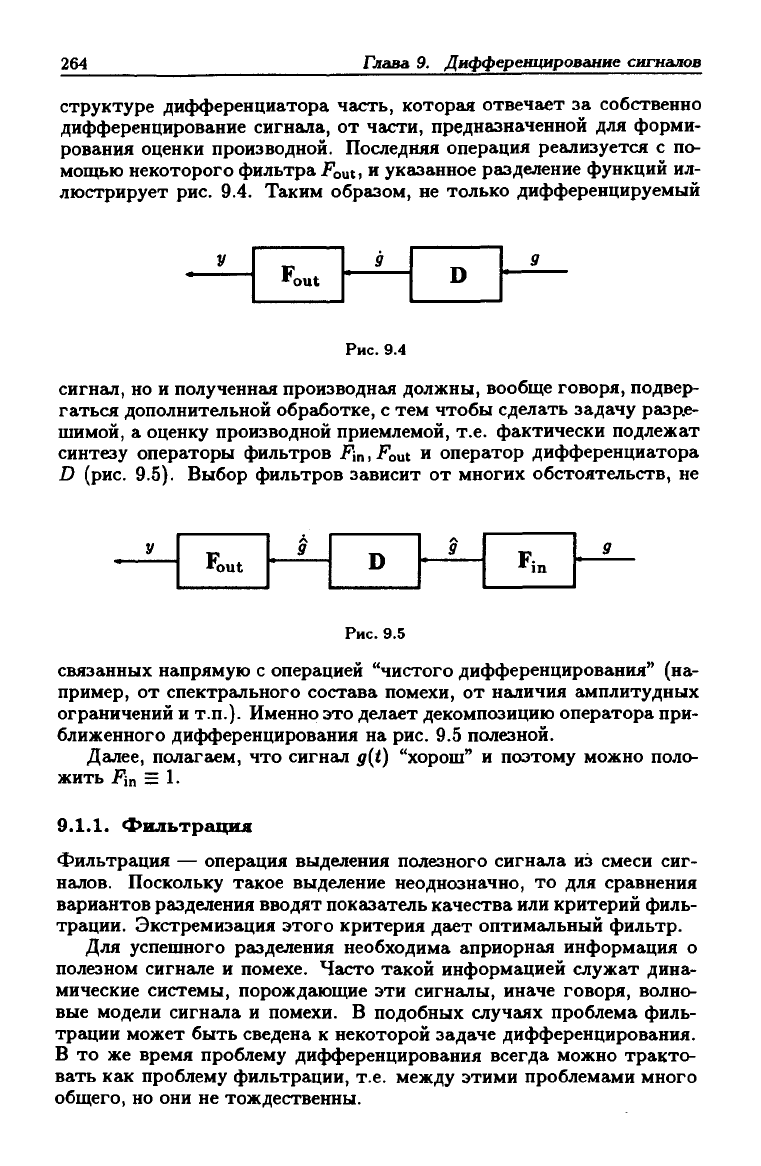
люстрирует рис. 9.4. Таким образом, не только дифференцируемый

'^out

Рис. 9.4

сигнал, но и полученная производная должны, вообще говоря, подвер-

гаться дополнительной обработке, с тем чтобы сделать задачу разре-

шимой, а оценку производной приемлемой, т.е. фактически подлежат

синтезу операторы фильтров Fim^out и оператор дифференциатора

D (рис. 9.5). Выбор фильтров зависит от многих обстоятельств, не

rout

Рис. 9.5

связанных напрямую с операцией "чистого дифференцирования" (на-

пример, от спектрального состава помехи, от наличия амплитудных

ограничений и т.п.). Именно это делает декомпозицию оператора при-

ближенного дифференцирования на рис. 9.5 полезной.

Далее, полагаем, что сигнал g{t) "хорош" и поэтому можно поло-

жить Fin = 1-

9.1.1.

Фильтрация

Фильтрация — операция выделения полезного сигнала из смеси сиг-

налов. Поскольку такое выделение неоднозначно, то для сравнения

вариантов разделения вводят показатель качества или критерий филь-

трации. Экстремизация этого критерия дает оптимальный фильтр.

Для успешного разделения необходима априорная информация о

полезном сигнале и помехе. Часто такой информацией служат дина-

мические системы, порождающие эти сигналы, иначе говоря, волно-

вые модели сигнала и помехи. В подобных случаях проблема филь-

трации может быть сведена к некоторой задаче дифференцирования.

В то же время проблему дифференцирования всегда можно тракто-

вать как проблему фильтрации, т.е. между этими проблемами много

общего, но они не тождественны.

9.1.

Постановка

задачи диффереицировгшия 265

Дело даже не столько в том, что задача фильтрации обычно рас-

сматривается в стохастической постановке, а задача дифференциро-

вания — в детерминированной. Основное различие сводится к тому,

что обычно для решения задачи дифференцирования требуется мень-

ший объем априорной информации, нежели объем, необходимый для

решения задачи фильтрации.

9.1.2. RC-цепочка

В приложениях и по сей день для приближенного дифференцирования

используются простейшие дифференциаторы, реализуемые на пассив-

ных электроцепях. Наиболее известным дифференциатором этого

типа является ЛС-цепочка (рис. 9.6). Здесь д — входное напряже-

г-И^

9 -' i ] \\R

Рис. 9.6

ние,

у — выходное напряжение, i — сила тока, R и с — параметры

цепочки, сопротивление и емкость соответственно. По закону Ома

-Ri + 'fidt, y = Ri.

Дифференцируя это выражение и исключая силу тока i, получаем

дифференциальное уравнение

if + {l/T)y = g, (9.4)

где Г = КС — постоянная времени дифференцирования. Общее ре-

шение уравнения (9.4) имеет вид

У= е-^/^у{0)+Тд{1-е-*/^).

^ V ' > ^ '^

свободное вынужденное

движение движение

Исследуем дифференцирующие свойства ДС-цепочки, рассматри-

вая лишь вынужденную компоненту (у(0) = 0) решения (выхода), так

как свободное движение экспоненциально затухает. Пусть сначала

д = const.

266

Глава 9. Дифференцирование сигналов

В этом случае из уравнения

у = Ту(1-е-'/^)

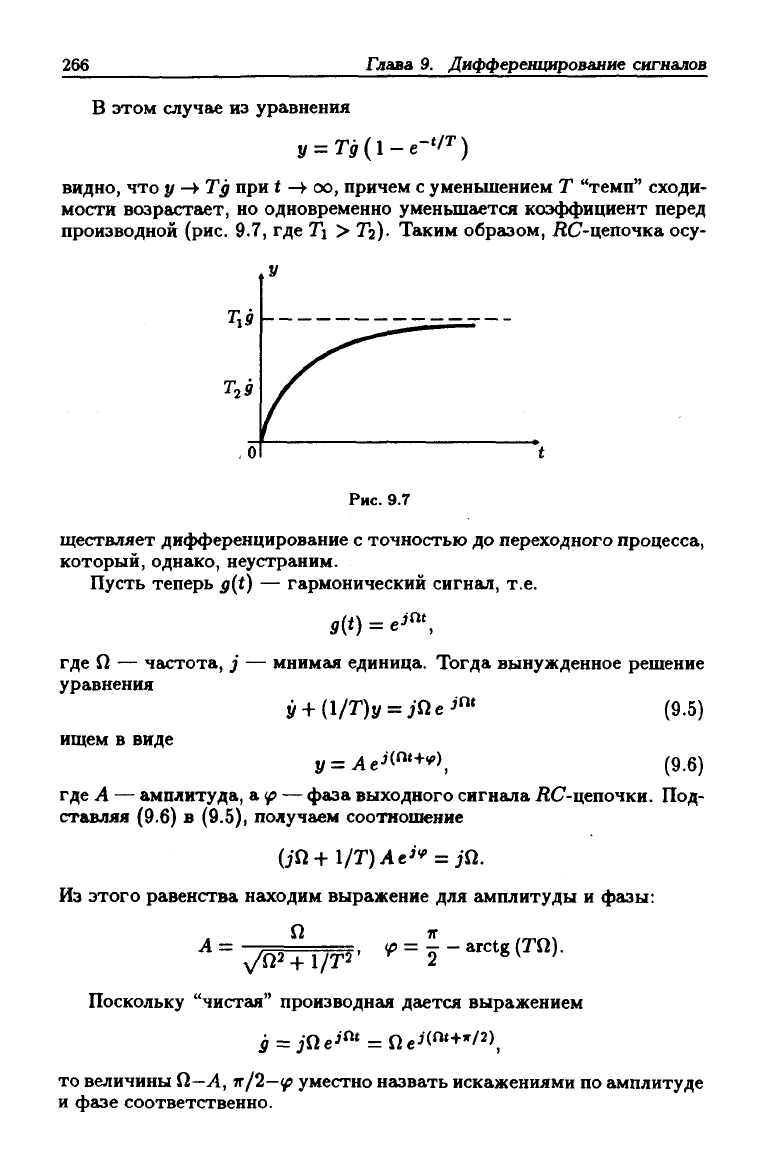
видно, что у -^Тд при f -> оо, причем с уменьшением Т "темп" сходи-

мости возрастает, но одновременно уменьшается коэффициент перед

производной (рис. 9.7, где 7i > Тг). Таким образом, ДС-цепочка осу-

Рис. 9.7

ществляет дифференцирование с точностью до переходного процесса,

который, однако, неустраним.

Пусть теперь g{t) — гармонический сигнал, т.е.

</(<) = е^"',

где

О,

— частота, j — мнимая единица. Тогда вынужденное решение

уравнения

у-К1/Г)у = ;Пе>"* (9.5)

ищем в виде

y = ^gj(nt+v)_ (9.6)

где А — амплитуда, а

у>

— фаза выходного сигнала ДС-цепочки. Под-

ставляя (9.6) в (9.5), получаем соотношение

(jfi + l/r)Ae^*' = jn.

Из этого равенства находим выражение для амплитуды и фазы:

А= , „ у>= ^-arctg(Tn).

Поскольку "чистая" производная дается выражением

то величины П—Л, itl2—ip уместно назвать искажениями по амплитуде

и фазе соответственно.

9.1.

Постановка

задачи

дифференцирования

267

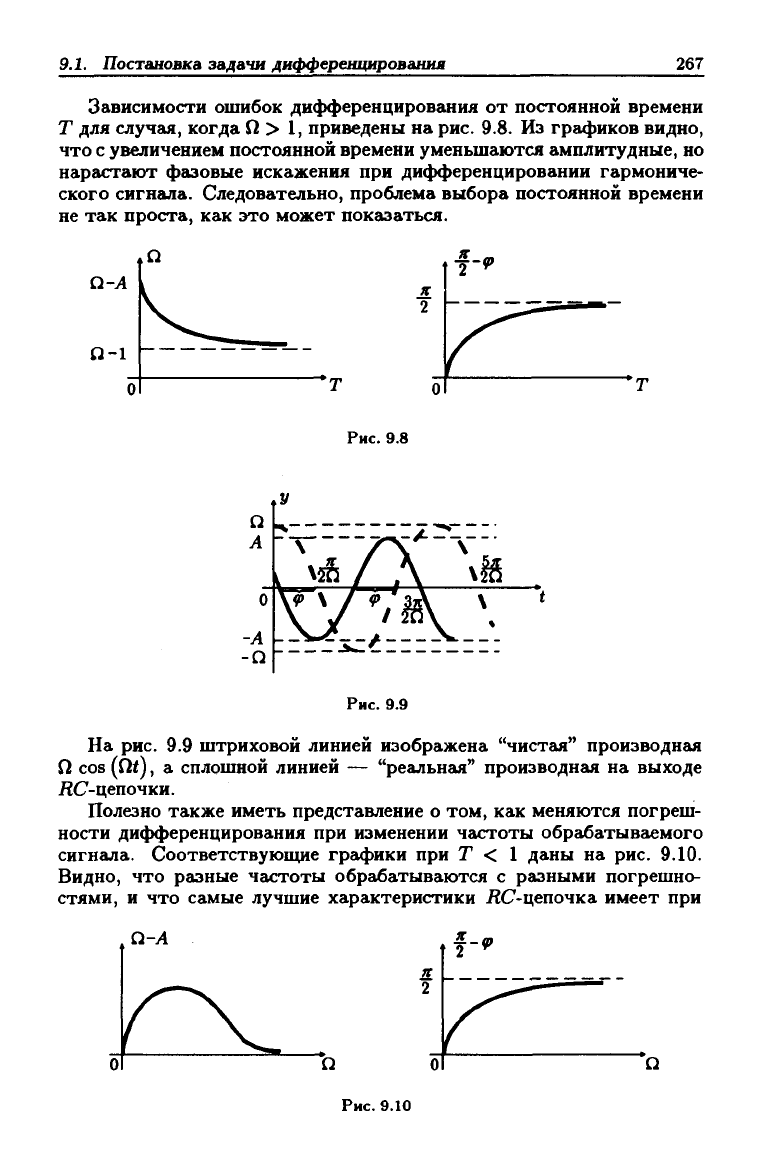
Зависимости ошибок дифференцирования от постоянной времени

Т для случая, когда Q > 1, приведены на рис. 9.8. Из графиков видно,

что с увеличением постоянной времени уменьшаются амплитудные, но

нарастают фазовые искажения при дифференцировании гармониче-

ского сигнала. Следовательно, проблема выбора постоянной времени

не так проста, как это может показаться.

Q-A

П-1

^Т

Рис. 9.8

*У

•А

Рис. 9.9

На рис. 9.9 штриховой линией изображена "чистая" производная

П cos (Qf), а сплошной линией — "реальная" производная на выходе

ЛС-цепочки.

Полезно также иметь представление о том, как меняются погреш-

ности дифференцирования при изменении частоты обрабатываемого

сигнала. Соответствуюпще графики при Т < 1 даны на рис. 9.10.

Видно, что разные частоты обрабатываются с разными погрешно-

стями, и что самые лучшие характеристики ЛС-цепочка имеет при

Q-A

Рис. 9.10

268

Глава 9. Дифференцирование сигналов

П -> О, т.е. при дифференцировании постоянного сигнала. При нали-

чии помехи, т.е. когда дифференцируется сигнал g{t) = е^^* + ее-''^*,

где частота помехи

3> П, а амплитуда е <^\, выход ЛС-цепочки при

у(0) =

можно представить в виде суммы у

—

I/n(0 +

!/w(Oi

где первая

компонента — оценка производной полезного сигнала, а уо, — оценка

производной помехи. Поскольку для компоненты

УшЩ

справедливы

приводившиеся выше формулы (9.5), (9.6) и связанные с ними, то вно-

симый ею дополнительный вклад в погрешность дифференцирования

определяется ее амплитудой А^ и фазой

^ш'-

Аш —

Тш

х/1 + (Та;)2'

у>„ =arctg(-Ta)).

Из выражений для амплитуды и фазы следует, что для устранения

вредного влияния помехи следует увеличивать постоянную времени

ДС-цепочки, но тогда возрастают фазовые искажения в полезной со-

ставляющей. Поэтому здесь возможен компромисс. Лучший выход,

однако, может состоять в поиске таких схем дифференцирования, в

которых имеется несколько свободных параметров, позволяющих не-

зависимо решать задачу "фильтрации" помехи и уменьшения ампли-

тудных и фазовых искажений.

Перейдем к рассмотрению подобных схем дифференцирования, но

прежде заметим, что передаточная функция ЛС-цепочки имеет вид

s+l/T'

который нетрудно установить по ее дифференциальному уравнению

Такой передаточной функции соответствует упрощенная струк-

турная схема на рис. 9.11, которую можно развернуть в виде системы,

представленной на рис. 9.12, где z — выход следящей системы, е — ее

S + 1/T

Рис.

9.11

Рис.

9.12

ошибка, в схемах всего один настраиваемый параметр Т, что и пре-

допределяет их возможности. Если вместо тождественного преобра-

зования в прямом канале использовать иные законы обратной связи,

то можно рассчитывать на получение лучших дифференциаторов.

9.1.

UocTSLHOBKa

задачи дифференцирования 269

9.1.3.

Дискретно-разностные аппроксимации

К улучшенным методам дифференцирования относятся методы, осно-

ванные на использовании дискретных разностей различных порядков

дифференцируемой функции. Например, оценкой производной функ-

ции g{t) может служить разность

Ь"'"-',"-"'^^,

(9.7)

где h = const > 0. Заметим, что для линейных функций эта оценка

(9.7) производной совпадает с ее точным значением. В общем случае

имеет место равенство

g{t) = g{t -h)+ g{t) h + g{t + dh) —,

где d — некоторое число из интервала

[0,1],

и, следовательно, оценка

(9.7) имеет погрешность порядка О(Л^).

Использование дискретных значений в (г + 1)-й точке для форми-

рования оценки

к=0

при надлежащем выборе параметров а* позволяет повысить точность

аппроксимации до

0{h^).

Кажется, что устремлением Л

—> О

задача

дифференцирования исчерпывается. Однако это не так и при наличии

помехи возникают проблемы, родственные описанным в предыдущем

пункте. Именно, пусть вместо g{t) дифференцируется по схеме (9.7)

сигнал де = g(t) + е sin uit, тогда оценка его производной д^ дг1ется

выражением

^ 9e{t)-9^t-h) g(t)-g{t + h) ,

д^ = 7 = 7 +

^^ '• (9.8)

+— [sin ut

—

sin u{t

—

h)].

Ho sin w(t

—

h) = sin ut cos wh

—

cos uit sin uh, и при u)h <^ 1

cos wA S 1

—

uh, sin uh

uh,

поэтому справедливо приближенное равенство

sin u{t

—

Л) S sin ut

—

иh{sin ut + cos ut).

Следовательно, помеха вносит в оценку (9.8) дополнительную и,

вообще говоря, сколь угодно большую погрешность

д^ °i д

—

ей {sin ut + cos ut),

неустранимую при уменьшении Л

—>

270

Глава 9. Дифференцирование сигналов

В некоторых ситуациях качество такого дифференцирования мо-

жет быть повышено использованием идеи фильтрации, которая в раз-

ностных схемах эквивалентна операции усреднения. Именно, пусть

дифференцируемый сигнал д( есть аддитивная смесь полезного сиг-

нала д и случайной помехи ^ с нулевым средним, т.е. М( = 0. Для

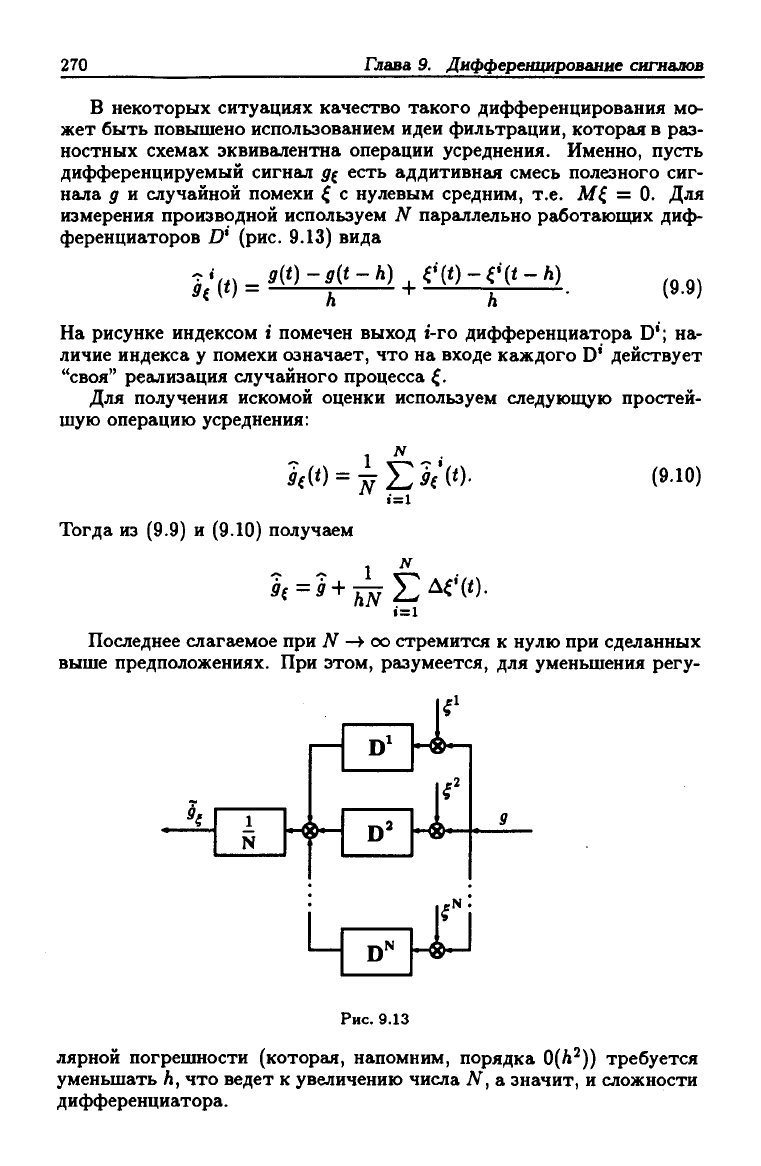
измерения производной используем N параллельно работающих диф-

ференциаторов D* (рис. 9.13) вида

5€(<)

^g(t)-g{t-h) ^ ^<{t)-C{t-h)

(9.9)

На рисунке индексом i помечен выход i-ro дифференциатора D'; на-

личие индекса у помехи означает, что на входе каждого D' действует

"своя" реализация случайного процесса ^.

Для получения искомой оценки используем следующую простей-

шую операцию усреднения:

1 ^

^«(<)=ЛгЕ

^До-

лг ^

(9.10)

Тогда из (9.9) и (9.10) получаем

1=1

^«=Ьг^Ед^'»

1=1

Последнее слагаемое при N -^

сх>

стремится к нулю при сделанных

выше предположениях. При этом, разумеется, для уменьшения регу-

"W—I

"оП^

I—r~^N~LiJ

Рис. 9.13

лярной погрешности (которая, напомним, порядка 0(Л^)) требуется

уменьшать Л, что ведет к увеличению числа N, а значит, и сложности

дифференциатора.