Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

9.5.

Нестандартные

дифференцирующие

системы

291

через конечное время в точке е =

возникает скользящий режим. В

этом случае эквивалентное значение разрывного сигнала определено

равенством

ksgn^qe = £,

после подстановки которого в уравнение (9.44) получаем уравнение

изменения ошибки дифференцирования

г/Г + е = т'д.

Если выполняется (9.46), то справедлива следующая оценка погреш-

ности дифференцирования:

\£(t)\<TM.

(9.48)

Из (9.47), (9.48) устанавливаем неравенство, ограничивающее снизу

величину разрывов:

it > тМ.

Выводы:

• Амплитуда разрывов в идеале может быть сделана сколь угодно

малой.

• В реальной схеме постоянного фильтра т >

Тст,

где

Тсг

определя-

ется неидеальностями переключений, поэтому амплитуда разры-

вов не может быть меньше fccr >

ТстМ.

• В рассмотренном дифференциаторе класс допустимых сигналов

расширен до сигналов с ограниченной д.

9.5.2. Нестандартный бинарный дифференциатор

Если предыдущий нестандартный дифференциатор основывался на

следящей системе, то рассматривг^емый ниже дифференциатор бази-

руется на принципиально иной идее. Суть ее проясняет рис. 9.41. Из

^ -

Рис. 9.41

рисунка видно, что в качестве оценки производной сигнала g{t) пред-

лагается использовать ошибку "слежения"

е = д - Z.

292 Глава 9. Дифференцирование сигналов

Смысл этой идеи можно пояснить следующим образом. В стан-

дартной следящей системе е = О и выход регулятора Ну совпадает

с производной д. Если к сигналу g(t) добавляется помеха qsinut, то

на выходе регулятора имеем сигнал д + qujcosut, причем возможно,

что gw 3> 1. Поскольку на выходе регулятора всегда имеются ампли-

тудные ограничения, то они будут постоянно нарушаться и оценка

производной искажается. Поэтому возникает идея о "снятии" произ-

водной до регулятора, так как в этом случае можно рассчитывать на

уменьшение негативного влияния амплитудных ограничений.

Проведем предварительный анализ схемы на рис. 9.41. Ее описы-

вает операторное соотношение

Ли

е = д- z = д -е,

где S — символ операции дифференцирования. Следовательно,

Для того чтобы дифференциатор давал сколь угодно малые фазовые

и амплитудные искажения, необходимо выполнение равенства

при назначенной по произволу постоянной времени г = const > 0. Из

сравнения (9.49) и (9.50) находим требуемое для этого выражение для

оператора

Ry = {T-l)s+l. (9.51)

Из формулы (9.51) видно, что для решения этой задачи (т.е. задачи

дифференцирования) линейными средствами требуется оператор "чи-

стой" производной. Получается порочный круг, разорвать который

можно только использованием эффектов, наблюдаемых в нелинейных

системах.

Здесь уместно напомнить, что в главе б (0-теория). уже возни-

кала сходная ситуация, когда в результате использования трех типов

обратной связи (К-, КО- и 0-связей) удавалось получать оператор

вида (9.51), т.е. оператор, преобразующий ошибку регулирования xi

во взвешенную сумму ошибки и ее производной:

и =

{-к/5)

а -

i-k/S)

(ii + dxi)

Но u = fixi, и из сравнения этих выражений находим, что действие fx

эквивалентно действию оператора

Ru = i~kfS)(s + d).

9.5.

Нестандартные

дифференцирующие системы

293

Воспользуемся рекомендациями КО- и 0-теорий. В результате по-

лучим структурную схему, изображенную на рис. 9.42. В этой схеме

^' 6h ^

\9 '

* ' •

1 ^

3 ,^

*•

Нд

К,

1 ^

tiy

Ф=

' N.

)

) 9

Рис. 9.42

следует задать операторы КО- и 0-регуляторов Д^ и Rf,, соответ-

ственно, бинарную операцию By и задатчик

Se •

Штриховкой выделен

регулятор Ry.

Если интересоваться лишь принципиальными возможностями ис-

следуемой схемы, то естественно воспользоваться результатами О-

теории и выбрать операторы R^, Rp, Se и бинарную операцию By в

виде

R^, : fi = ksgn (ге, «г = е*

—

е, к = const > О,

Rp : р = q(i, q = const > О,

Se : Те' +

СрС'

= е, с^ = с -|- ^, с = const > О,

By : J/ = ВуС = fie.

Указанный выбор продиктован следующими соображениями. Если

ошибка (т = О, то е = е* и из уравнения задатчика Se получаем

Те +

СрС

= е.

Но

Ср

= с + qfi, поэтому последнее уравнение может быть переписано

в виде

Те + {с

—

1)е = —q/ie.

294

Глава 9. Дифференцирование сигналов

Это означает, что "действие" операторной переменной ft по эффекту

эквивалентно "действию" оператора

_ Г. + (с-1)

Сравнивая это выражение с требуемым

Ry = {T-l)s+l,

получаем соотношения для расчета параметров схемы

1-г=-,

l = i^, (9.52)

Ч Я

которые нетрудно удовлетворить. В итоге получаем требуемое урав-

нение

тё

+ е= д.

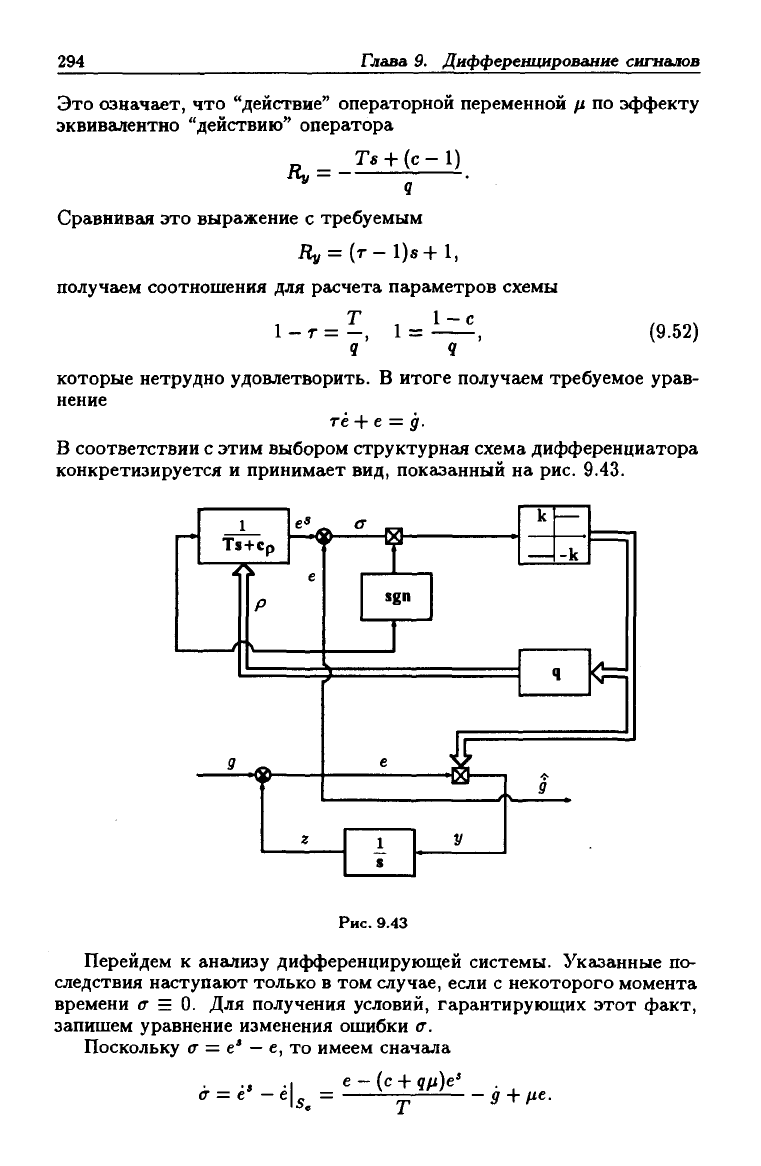
В соответствии с этим выбором структурная схема дифференциатора

конкретизируется и принимает вид, показанный на рис. 9.43.

Ts+cp

••V

9 «

•ч V

sgn

-к

1Г

Рис. 9.43

Ч|—1

Перейдем к анализу дифференцирующей системы. Указанные по-

следствия наступают только в том случае, если с некоторого момента

времени

<т

= 0. Для получения условий, гарантирующих этот факт,

запишем уравнение изменения ошибки сг.

Поскольку

(Т

= е*

—

е, то имеем сначала

= e'-eL = —z~ g + fie.

9.5. Нестандартные дифференцирующие

системы

295

Но е, = ст + е, поэтому

1-е с + g/i Д g \

^ е ^ <т , +

^е(^1

^j.

Из соотношений (9.52) следуют равенства

1—с 1 с

1 —

9 ,9 1" g

Г ~1-г' Г~д(1-г)' Т~ 1-т' Т~

(9.53)

1-т'

поэтому (9.53) можно переписать в виде

{l-q +

q(i)(T

. г

сг

= :; JZ ; 9-

И^-.

1-г

g(l-r) " '^ 1-т-

Поскольку

= к sgn

((те),

то окончательно получаем уравнение

Заметим теперь, что ничто не препятствует выбору параметра q

достаточно малым, например таким что

q{k+1)<1.

(9.55)

Тогда коэффициент (напомним, что \ft\ < к)

1-q + qfi

q{l -

т)

>0.

Для того чтобы в точке

<т

= 0 существовал скользящий режим, следует

позаботиться, как это следует из (9.54), о выполнении неравенства

<^{е

- 9 +

тд

- A;r|e|sgn (т) < 0.

По крайней мере в малой окрестности точки

<т

это условие выпол-

нено,

если

\д\

< k, (9.56)

поскольку при этом е = д.

Таким образом, если выполнены соотношения (9.55), (9.56), то при

начальных условиях из некоторой окрестности <г = О через конеч-

ное время возникает скользящий режим, поддерживающий требуемое

равенство <т = 0. Вследствие этого наступают описанные ранее бла-

гоприятные последствия, а именно:

296

Глава 9. Дифференцирование сигналов

• использование разрывной стг1билизирующей обратной связи не вле-

чет необходимости использования в данном случае "сглаживаю-

щего"

выходного фильтра, что является обязательным в других

разрывных дифференцирующих системах, однако для получения

старших производных такие "сглаживающие" фильтры могут по-

требоваться.

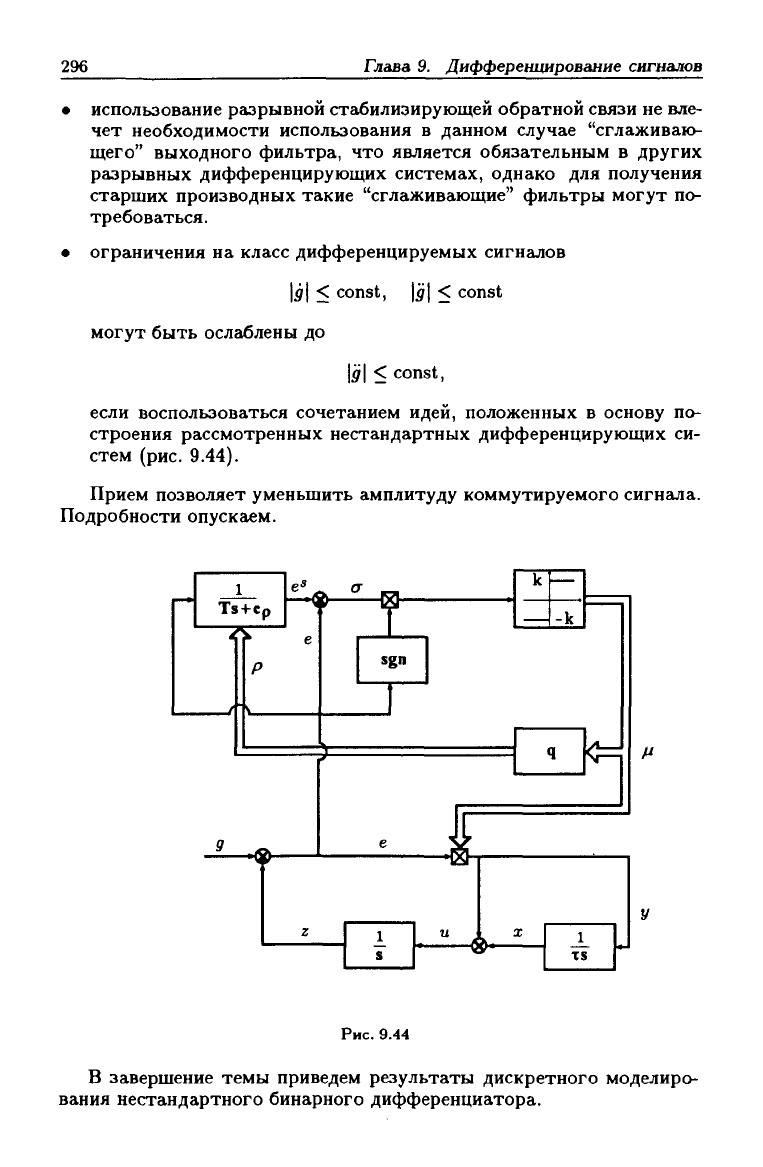
• ограничения на класс дифференцируемых сигналов

l^fl < const, |<;| < const

могут быть ослаблены до

< const,

если воспользоваться сочетанием идеи, положенных в основу по-

строения рассмотренных нестандартных дифференцирующих си-

стем (рис. 9.44).

Прием позволяет уменьшить амплитуду коммутируемого сигнала.

Подробности опускаем.

Ts + Cr

/Л

^-^^на

sgn

Рис. 9.44

В завершение темы приведем результаты дискретного моделиро-

вания нестандартного бинарного дифференциатора.

9.5.

Нестандартные

дифференцирующие

системы

297

9.5.3.

Результаты дискретного моделирования

нестандартного бинарного дифференциатора

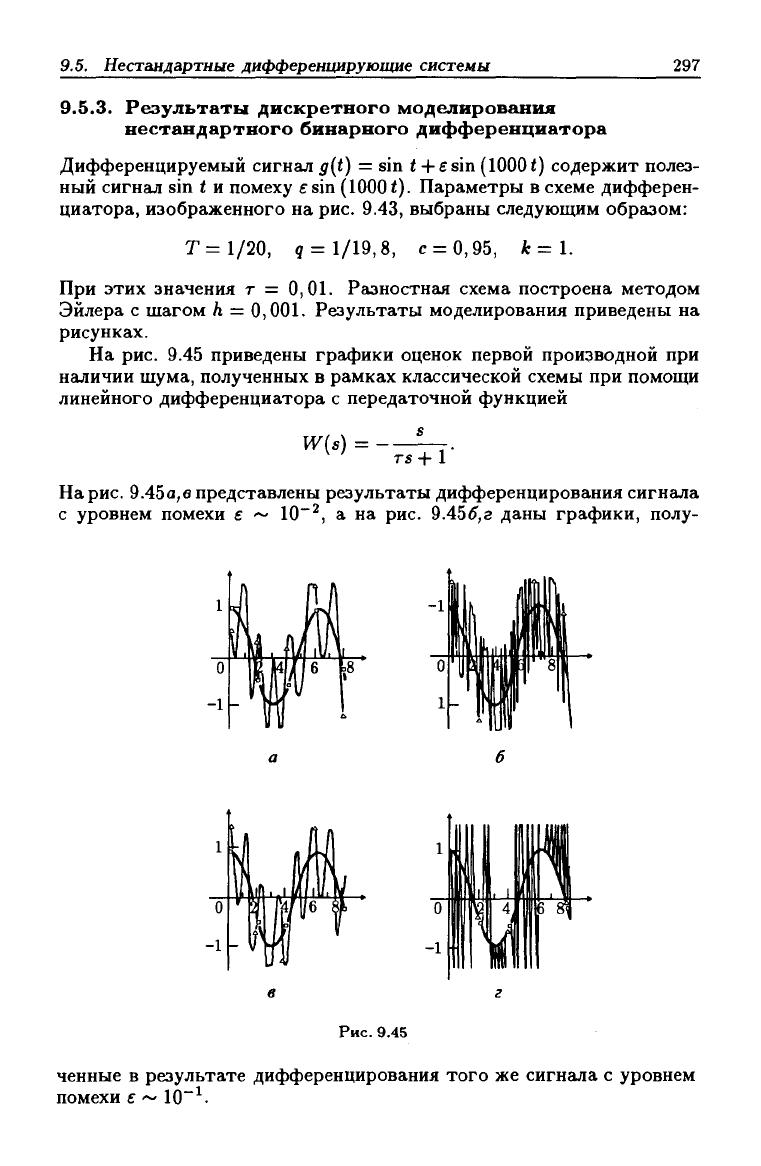
Дифференцируемый сигнгиг g{t) = sin t +

sin (10001) содержит полез-

ный сигнал sin t и помеху esin (1000

<).

Параметры в схеме дифферен-

циатора, изображенного на рис. 9.43, выбраны следующим образом:

Т=1/20, 9 =

1/19,8,

с = 0,95, к=1.

При этих значения т = 0,01. Разностная схема построена методом

Эйлера с шагом h =

0,001.

Результаты моделирования приведены на

рисунках.

На рис. 9.45 приведены графики оценок первой производной при

наличии шума, полученных в рамках классической схемы при помощи

линейного дифференциатора с передаточной функцией

W(s) = -

TS+1

На

рис.

9.45а,в представлены результаты дифференцирования сигнала

с уровнем помехи е -^ 10~^, а на рис. 9.456,г даны графики, полу-

-1

Мш1

Щт

Рис. 9.45

ченные в результате дифференцирования того же сигнала с уровнем

помехи е ~ 10"^.

298

Глава 9. Дифференцирование сигналов

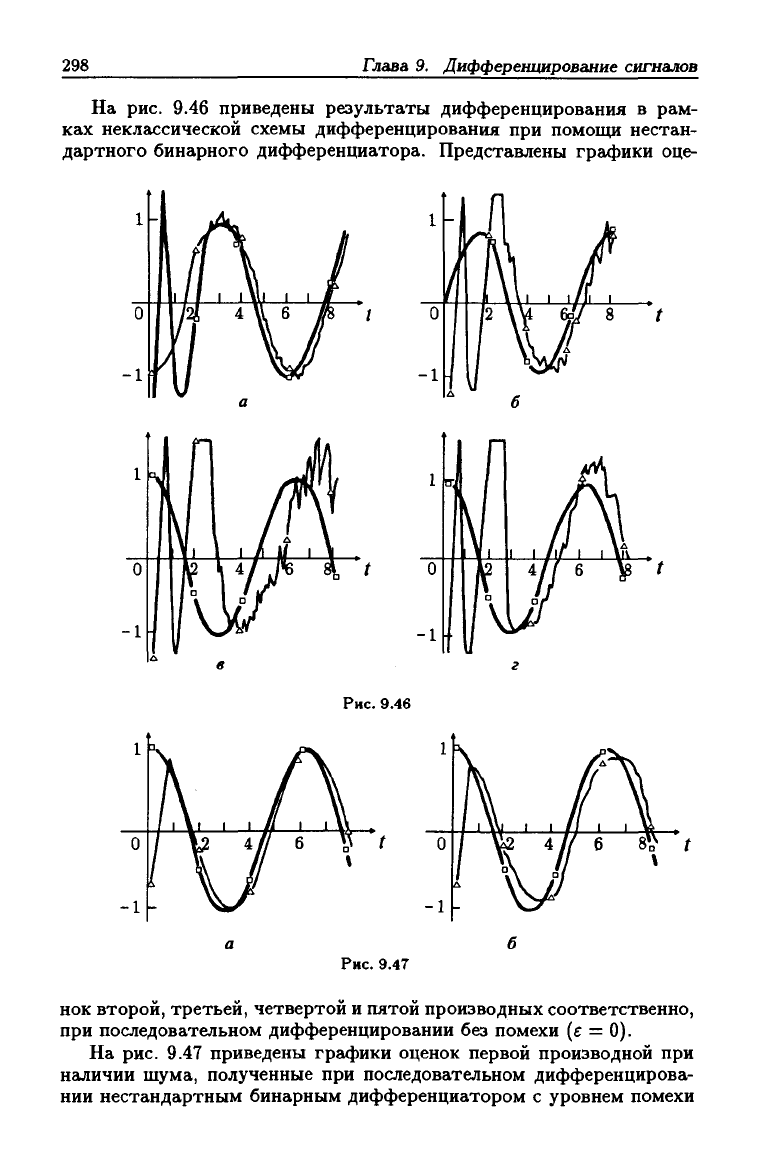
На рис. 9.46 приведены результаты дифференцирования в рам-

ках неклассической схемы дифференцирования при помощи нестан-

дартного бинарного дифференциатора. Представлены графики оце-

-1

• '!}

t о

Рис.

9.46

-1 -

Рис.

9.47

нок второй, третьей, четвертой и пятой производных соответственно,

при последовательном дифференцировании без помехи (е = 0).

На рис. 9.47 приведены графики оценок первой производной при

наличии шума, полученные при последовательном дифференцирова-

нии нестандартным бинарным дифференциатором с уровнем помехи

9.5.

Нестандартные

дифференцирующие

системы

299

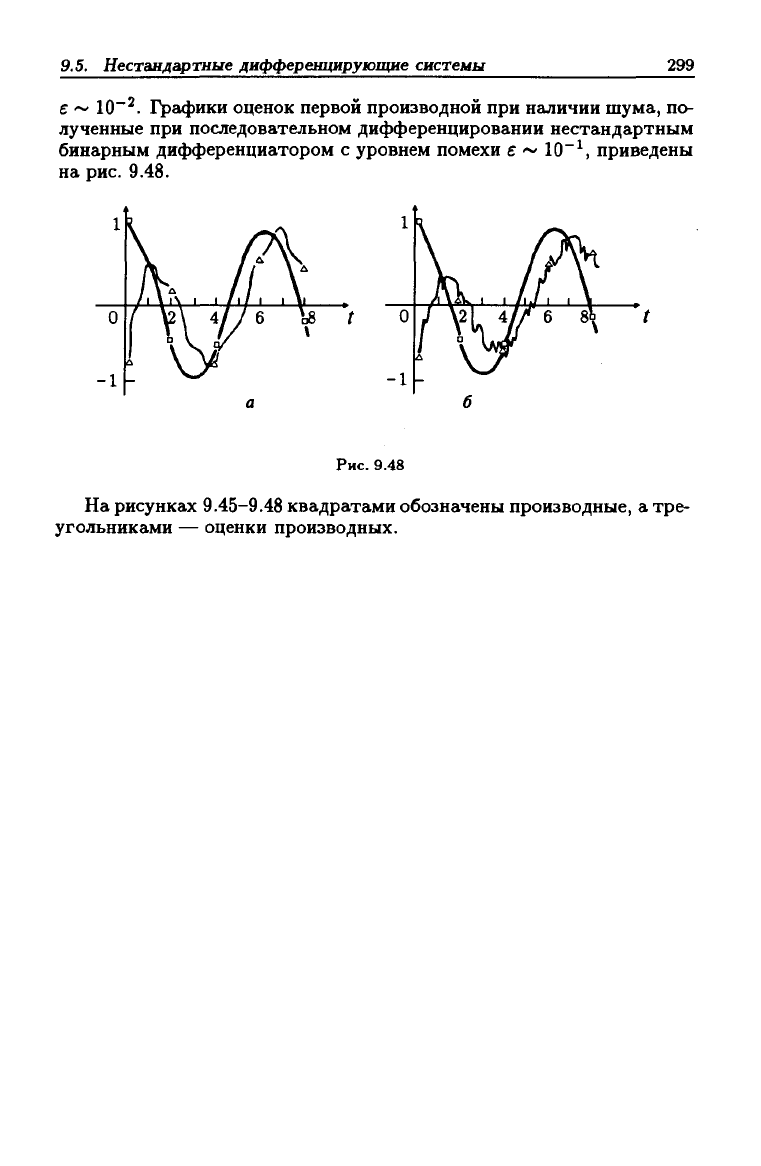
е ~ 10"^. Графики оценок первой производной при наличии шума, по-

лученные при последовательном дифференцировании нестандартным

бинарным дифференциатором с уровнем помехи е ~ 10"^, приведены

на рис. 9.48.

Рис. 9.48

На рисунках 9.45-9.48 квадратами обозначены производные, а тре-

угольниками — оценки производных.

Глава 10

Субоптимальная стабилизация

неопределенного объекта

Рассмотрим случаи, когда задача оптимальной стабилизации неопре-

деленного объекта решается точно или приближенно. Подход к реше-

нию базируется на сочетании идей оптимальной стабилизации, асим-

птотической инвариантности и теории бинарного управления. Инва-

риантность поля экстремгшей к факторам неопределенности служит

несущим элементом развиваемой конструкции. При этом от факторов

неопределенности зависит лишь оптимальная обратная связь. Для ее

приближенной реализации используются новые типы обратной связи и

методы бинарного управления. Проводится сравнение предлагаемого

подхода с известными методами: усреднения, гарантированного ре-

зультата, глубокой обратной связи и т.п.

10.1.

Постановка задачи оптимальной стабилизации

Оформление оптимальной стабилизации в самостоятельное направле-

ние теории оптимального управления в детерминированной поста-

новке уходит своими корнями к трудам А.А. Летова, Р. Беллмана,

А.А. Красовского и в стохастической постановке — к трудам Р. Кал-

мана. В результате многолетних усилий была создана теория АКОР

(аналитического конструирования оптимальных регуляторов).

Центральное место в теории АКОР занимает проблема синтеза

оптимальной обратной связи, стабилизирующей детерминированный

или стохастический объект в условиях, когда имеется полигл инфорь

мация о его поведении и ха'рактеристиках внешних сил. В реальных

условиях информация об объекте и действующих на него возмуще-

ниях всегда неполна, а так как оптимальное решение, как правило,

весьма чувствительно к вариациям условий задачи, то рекомендации

этой теории могут быть юяты только за основу и редко используются

на практике.

Возможности теории АКОР несколько расширяются при сочета-

нии ее методов с методами адаптивного управления. Внутренние

ограничения теории адаптивного управления не могли привести к

универсальным методам оптимальной стабилизации при неопределен-

ности, и потому рассматриваемая проблема сохраняет актугшьность.

Требуется новый взгляд на проблему оптимального управления при

неопределенности. В частности, представляет интерес выделение тех