Емельянов С.В. Новые типы обратной связи
Подождите немного. Документ загружается.


10.6.
Методы теории
бинарного управления 311
Но A:|x|sgno-eq = —а^х, поэтому X = —fx, а значит, оптимальное
значение функционала, найденное таким образом, инвариантно к па^
раметру а.
Если же действовать более аккуратно, то можно заметить, что
х = a^a;^ + 2aifcx|r|sgn(req + fc^a;^ = (Аг^-а^ -2а'у)х^,
и если а = const, то оптимальное значение функционала зависит от
параметра а и дается выражением
ЛГИ = \
1 + \{к^ - а2 - 2ау)
Т
1 ,2
Следовательно, при использовании методов клги;сической теории
систем переменной структуры в рассматриваемой задаче минимум
функционала не фиксирован и определяется конкретным значением
параметра а. В этом смысле рассматриваемая задача оптимального
управления методами СПС не решается. Причина состоит в том,
что интегрант функционала нелинеен по разрывному управлению. В
связи с этим представляют интерес методы оптимальной стабилиза-
ции, обеспечивающие движение по экстремали непрерывным управле-
нием.
10.6.2.
Бинарная стабилизация с интегральной КО-связью
Движение, сколь угодно близкое к оптимальному, можно обеспечить
непрерывным бинарным управлением с интегральной КО-связью
/i =
asgn I К+ук|| »;|.
где а = const >
О
— достаточно большое число, к > А^, как и ранее.
Для того чтобы убедиться в этом, проведем замену переменного
(Г
= ^ж и тогда получим уравнение движения
^ =-(l+OK+A*). /' = asgn
е.^к,
Поскольку /i —> /ieq = ^ SgH^q ^ ПрИ О —»^ ОО И ПрОЦеСС ^(t) СТ£1бИЛИЗИ-
руется в нуле, то нетрудно понять, что при конечном, но достаточно
большом а процесс ^(t) будет стабилизирован в некоторой окрестно-
сти нуля
1^1
< Si
с константой Si = Si{a) такой, что Si(a)
—¥ О
при а
—>
оо.
Пусть
Г)
= ц
—
/jeq. Тогда из предыдущего следует, что
\г}\
< «52,

312
HasLBa
10.
Субоптимальная
стабилизация
где константа ^2 = <^2(л) и 62(0)
—> О
при а
—>
оо. В этих обозначениях
для интегранта функционала задачи F справедлива оценка
•'^--'bmw-^^"-
.2
и, следовательно, для оптимального значения функционгиа J^^ спра-
ведливо неравенство
°Р*-
27^(1-(Ji)2 7'
из которого следует, что J^^
—>
XQ/T
при а -> оо, и теперь уместно го-
ворить о субоптимальной стабилизации в классе бинарных обратных
связей. Поскольку бинарные системы грубы по отношению к регу-
лярным и сингулярным возмущениям, то построенная субоптималь-
ная система управления также груба, и этим она выгодно отличг1ется
от систем стабилизации с большим коэффициентом усиления.
10.6.3.
Стабилизация с использованием
скользящего реясима 2-го порядка
При субоптимальной бинарной стабилизации x{t) ^ Xopt(t)- Однако
точное равенство х(<) = Xopt{t) все же можно обеспечить непрерыв-
ным управлением с конечного момента времени <,, если прибегнуть
к скользящему режиму 2-го порядка. Вновь рассмотрим бинарную
систему управления в координатах
i^,fi)
:
^ = -(i+OK +
/i)-
Тогда при
О
< р < 1/2 и достаточно больших константах а и А алго-
ритм управления вида fi = fii + fi2, где
обеспечивает стабилизацию ^ в нуле за конечное время t,, которое
может быть сделано сколь угодно мгшым, если ^(0) = 0. Потери на
поиск при этом определяются равенством
t.
^J^ = •/o1>t - -^opt = jiF - Fopt) dt,
0
И, следовательно, скользящие режимы 2-го порядка также открывают
возможность субоптимального управления неопределенным объектом.
10.6.
Методы теории
бинарного управления
313
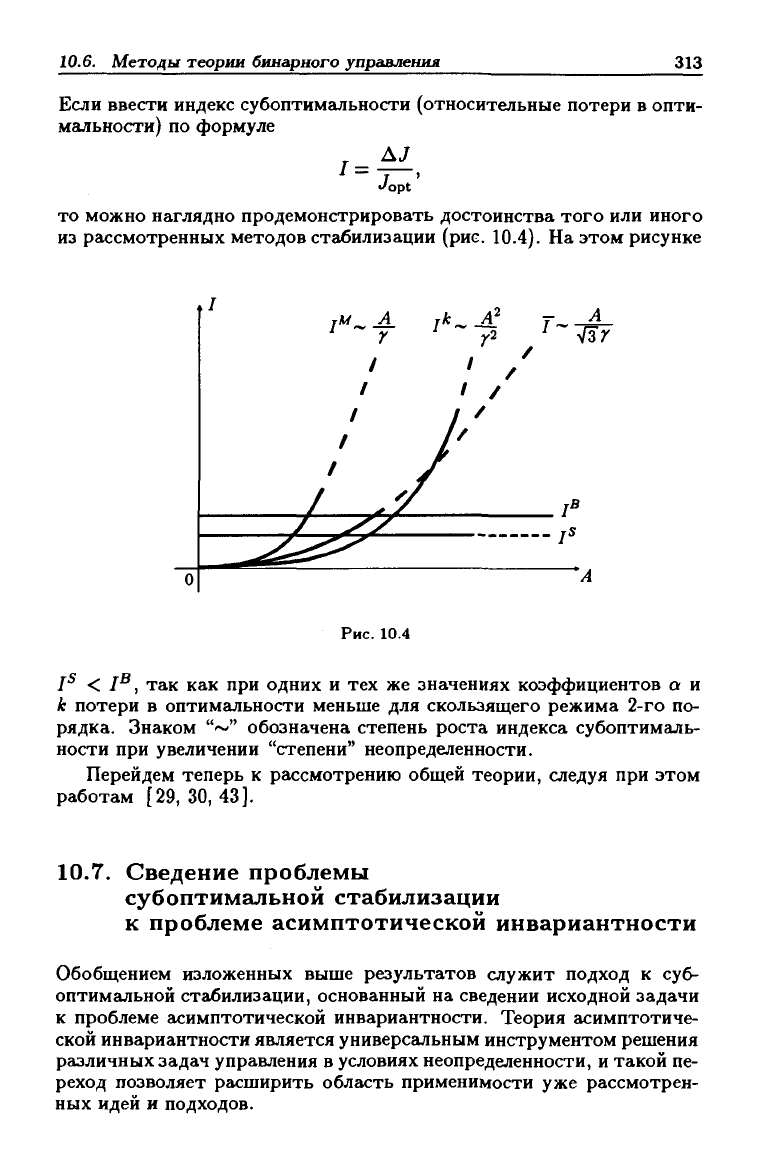
Если ввести индекс субоптимальности (относительные потери в опти-
мальности) по формуле
AJ
1 =
^opt
ТО
МОЖНО
наглядно продемонстрировать достоинства того или иного
из рассмотренных методов стабилизации (рис. 10.4). На этом рисунке
Рис.
10.4
jS < /В
rpg^j^
j^aK при одних и тех же значениях коэффициентов а и
к потери в оптимальности меньше для скользящего режима 2-го по-
рядка. Знаком "~" обозначена степень роста индекса субоптималь-
ности при увеличении "степени" неопределенности.
Перейдем теперь к рассмотрению общей теории, следуя при этом
работам [29, 30, 43].
10.7.
Сведение проблемы
субоптимальной стабилизации
к проблеме асимптотической инвариантности
Обобщением изложенных выше результатов служит подход к суб-
оптимальной стабилизации, основанный на сведении исходной задачи
к проблеме асимптотической инвариантности. Теория асимптотиче-
ской инвариантности является универсальным инструментом решения
различных задач управления в условиях неопределенности, и такой пе-
реход позволяет расширить область применимости уже рассмотрен-
ных идей и подходов.

314 Глава 10.
Субоптимальная стабилизация
10.7.1.
Основные понятия
теории асимптотической инвариантности
Пусть А — компактное множество и пара функций {х,
Uopt}
Для каж-
дого элемента а Е А минимизирует функционал в форме Лагранжа
J{u,a)= 1 L{t,x,u,a)dt + l{xo,xi)
to
при ограничениях
X
= f{t, X, и, а), x{to) = хо, x{ti) = xi, UEU.
Пусть, кроме того, оптимальное значение функционала не зависит от
элемента а € А, т.е.
J{uopt, а) = J(«opt) для любого а е А.
Здесь и далее х £ R", и — скалярное управление. Предполагается,
что функции /, i, / и классы А и U таковы, что решение задачи
оптимизации существует. Из сделанного предположения следует, что
оптимальное управление зависит от а, т.е. «opt = Uopt(t,x,a), и его
реализация, если возмущение а неизвестно, невозможна. Поэтому уме-
стен вопрос о приближении оптимального управления «opt в классе
допустимых обратных связей. Для оценки качества такого прибли-
жения используем индекс субоптимальности (относительные потери
в оптимальности)
, , _ 7(ц,а)-J(«opt)
'^"•''^- /(«opt) •
Понятие о качестве приближения вводится следующим определением:
если для любого е >
О
существует такая допустимая обратная связь
и £ и, что sup/(и, а) < е, то замкнутая система субоптимальна в
аел
классе управлений U.
Понятие субоптимальной системы стабилизации можно связать с
понятием асимптотической инвариантности.
Пусть е и 7 — произвольные положительные числа. Для некоторой
функции h{t, х) введем обозначения:
Ли,а = h(t, x{t;to,Хо,и, а)), а^ = hu,ai
—
Лц.а,-
Динамическую систему х = f{t,x,u,a) назовем (е,7)-экспоненциально
Л-инвариантной относительно возмущений а G Л в клг1ссе управлений
и, если найдется обратная связь и £11 я положительная при всех х фО
функция р(х) (р(0) = 0) такие, что при любых элементах ai, 02 € А
тл
каждого Хо ё R"
К|<£р(а;о)е-1'('-'°>, t>tQ.

10.7.
Асимптотическая инвариантность
315
Связь между субоптимальностью и экспоненцигиьной инвариант-
ностью рги:крывает следующее утверждение.
Утверждение 1. Пусть при некоторых положительных числах у,
Я11
Я2,
Яз
я произвольном £ >
О
выполнены предположения:
1) динамическая система х = f{t,x,u,a) является (ед1,7)-экспонеяця-
ально L-инвариантной относительно возмущений а Е А в классе
управлений и;
2) при любом управлении и &U существует элемент а, Е А такой, что
1{и,а*) <eq2\
3) при любых и ЕЫ, а Е А
\l{xo,x{ti;tQ,xo,u,a)) - l{xo,x(ti;to,xo,u,a»)) \ < едз-
Тогда динамическая система х = f(t, х,и,а) субоптимальна в классе
U
относительно лагранжиана L и существует такая реализуемая обрат-
ная связь «,, что
В приведенном утверждении указаны условия, при которых проб-
лема субоптимизации сводится к проблеме экспоненциальной инвари-
антности. Для последней р£1зработаны конструктивные методы син-
теза обратной связи, благодаря чему ее решение существенно упроща-
ется. В теории асимптотической инвариантности используются уни-
версальные достаточные условия экспоненциальной инвариантности,
являющиеся единой основой для получения законов управления, ре-
шающих конкретно поставленную задачу. Эти достаточные условия
могут быть сформулированы в виде следующего утверждения.
Утверзкдение 2. Положим
г){1)
= £р(хо) е"''^'"*"^ (7 > 0), и пусть
существуют такие константа g > О я непрерывная положительная
функция v{t) = v{t^Xu) > О, что:
Л) v{t) дифференцируема по t, когда v{t) >
т}{1);
2) v{to) < r)(to);
3) при некотором и ЕИ выполнено условие
«Я-7f |«(t)>f,(t) <0;
4) |<г„(<)| < qv{t,x{t)) при всех t >to, а Е А.
Тогда равномерно notnaEA
к„(<)|<£9РЫе-^('-*°),
т.е.
пря h = L имеет место (£,у)-экспоненциальная L-инвариант-
ность.

316 Глава 10.
Субоптимальная стабилизация
Покажем, как сформулированные выше достаточные условия экс-
поненциальной инвариантности используются в конкретных ситуа-
циях, на примере субоптимальной линейно-квадратичной стабилиза-
ции неопределенной системы.
•10.7.2.
Субоптимальная линейно-квадратичная стабилизация
Для линейного объекта и квадратичного функционала предложенную
выше схему синтеза субоптимального управления можно довести до
конца. Действительно, рассмотрим в R° при t >
О
линейный стацио-
нарный управляемый объект
х = Ах +
Ь{и
+ а), ж(0) = хо,
где а € Л — неизвестное возмущение, такое что
|a|<ai|a!|,
|d|<a2|j;|.
Здесь константы ai, 02 известны. Требуется построить реализуемую
обратную связь, минимизирующую функционал "полной" энергии
оо
J=IL{t)dt, L = x'^Px + x'^Qx, Р>0, Q>0.
о
Используя обозначения,
P = P + {A-bd'^)^Q{A-bd^), Q^b^Qb,
d=^^^,
v = u + d'^x + a, Ad = A-bd'^, d
G
R".
функционал и уравнение связи преобразуем к виду
со
7= f{x'^Px
+
Qv^)dt,
о
X
= AdX + bv.
Оптимальное решение преобразованной задачи известно и дается
выражением
'^opt = —^
X,
где к = Q ^b^R,
а,
R — решение уравнения Риккати
Р - RbQ-4R + RAd + а^Я = 0.
При этом поле экстремалей задачи описывгьется уравнением
X = {Ad-bk)x,

10.7.
Асимптотическая инвариантность
317
а оптимальное значение функционала находится по формуле
•^jpt = XQ RXQ.
Для того чтобы получить оптимальную систему стабилизации, не-
обходимо реализовать обратную связь
«opt = -кх - а, к = k + d^,
что,
разумеется, невозможно. Вместо этой нереализуемой обратной
связи используем обратную связь вида
и = —кх + Uj,
где для генерации компоненты щ воспользуемся методами бинарного
управления и изложенными выше принципами субоптимального упра-
вления и экспоненциальной инвариантности.
Пусть в схеме на рис. 10.2 динамический задатчик Sx определен
уравнением поля экстремалей задачи
х^=АкХ^,
х'^(0) = аго, Ак=А-Ьк.
Известно, что спектр ar{Ait) матрицы Л* расположен в левой от-
крытой комплексной полуплоскости, т.е. существует число 7о > О
такое, что для любого
А
£
(т{Ак)
выполнено условие ReA < —уо- Сле-
довательно, при некотором N > 1
В качестве Ли,а возьмем функцию
L = x'^Px + Q{uc + af.
При помощи достаточных условий экспоненциальной инвариант-
ности, сформулированных в предыдущем разделе, находим, что упра-
вляемая система будет экспоненциально L-инвариантна в рассматри-
ваемом классе обратных связей, если существует обратная связь Ug
такая, что
lim
t-foo
L{t)-x'^it){P + k'^Qk)x(t)
= 0.
Положим
щ = -ко\\х\\ц, /i = -asgn[(r +
/i|(r|],
где fco и а — положительные параметры, а функция
сг
является реше-
нием системы дифференциальных уравнений
&
+
l<T
= a-ko\\x\\ft /i =-asgn[(T4-/i|<T|], |/<(<о)| < 1-
Здесь I — произвольно назначаемое положительное число. Очевидно,
что функция
(т{1)
нам также неизвестна, но если пока отвлечься от

318 Глава
10.
Субоптимлдьиая стабилизация
этого обстоятельства, то ясно, что надлежащим выбором ко, а не-
сложно обеспечить выполнение следующих неравенств:
к1 <
s|ko||e-^S
t >
О,
\&\
< e?i||xo||e-^'. t > Г,
Var
<r
< е||го||, sup
\&\
< дгН^оН,
о [0,0
при некоторых положительных константах е, qi, дг и 7-
Из этих неравенств и уравнения
X
= АкХ +
Ь{&
+
1<г)
следует асимптотическая инвариантность системы, а вместе с ней и
ее субоптимальность. Таким образом, все свелось к оценке функции
(т(<),
и для этого годится асимптотический наблюдатель вида
? = с^х
—
^,
i =
c'^AkX
+ l(c'^x-0,
где с^б = 1. Нетрудно установить, что ошибка оценивания е =
<т —
?
удовлетворяет уравнению
ё
+
1е
=
О
и, следовательно, функция ? экс-
поненциально (с произвольно назначаемым показателем /) сходится к
функции
<т.
Отсюда следует, что свойство субоптимальности
сохрг1-
нится, если вместо
сг
в обратной связи использовать ее оценку а, т.е.
и = -кх - A!o||a;||/i,
it = -asgn[a + fi\a\], |;i(0)| < 1.
Таким образом, использование методов асимптотической инвари-
антности для оптимальной стабилизации при неопределенности по-
зволяет синтезировать обратные связи, робастно стабилизирующие
неопределенные объекты с качеством, сколь угодно близким к опти-
мальному. Решение задач оптимального управления в рамках теории
асимптотической инвариантности (ввиду универсальности последней)
позволяет рги:ширить классы неопределенных объектов, подлежащих
оптимизации.
В общем случае, задача оптимальной стабилизации в условиях не-
определенности не решается классическими методами, но их сочета-
ние с теорией новых типов обратной связи и идеей асимптотической
инвариантности позволяет решать задачу для достаточно широкого
класса неопределенных объектов. Этот факт и подтверждается в на-
стоящей главе. Развитие и обобщение этих положений дг^тся в рабо-
тах, ссылки на которые даны на стр. 133.

Заключение
Обратная связь "пронизывает" окружающую нас действительность:
она служит ключевым элементом биологической эволюции и естествен-
ного отбора; она обеспечивает регуляторный механизм в равновесных
системах, в частности в природных экосистемах, и является необхо-
димым элементом работоспособных экономических конструкций; на-
конец, она составляет основу саморегулирующихся и самоподдержи-
вающихся биосистем. Этот список легко продолжить. Но до сих пор
мы очень мало знгюм о механизме обратной связи, так как фактиче-
ски он никогда не являлся самостоятельным объектом исследования.
И на то есть причины.
Действительно, идея обратной связи почти очевидна, легко воспри-
нимается и в простых ситуациях ее применение не вызывает проблем.
Однако синтез обратной связи в нестандартной ситуации, как пра-
вило,
дается нелегко и требует нешаблонных решений. Это обусло-
влено отсутствием теории, объясняющей механизмы формирования
обратной связи. Как правило, эти механизмы ускользают от исследо-
вателя, поскольку они довольно сложны. Здесь ситуация аналогична
ситуации с другими законами естествознания. 6 свое время физик Ри-
чард Фейнман сказал о законе тяготения: "Закон действует сложно,
но его коренная идея проста. Это обстоятельство роднит все н£Ш1и
законы" [89].
Справедливости ради следует заметить, что регулярные попытки
изучения обратной связи предпринимаются и в теории автоматиче-
ского управления, и в бионике, и в экономических теориях. Однако в
этих дисциплинах почти всегда упор делается на использование обрат-
ной связи, а не на механизм ее формирования. Это естественно, ибо,
по мнению Энона, предметная наука вырабатывает правила решения
задачи, но не способы выбора этих правил.
Отсутствие правил второго уровня принуждает нас к необходимо-
сти угадывания закона обратной связи всякий раз, когда мы имеем
дело с нестандартной задачей, но новые идеи и принципы придумы-
вать очень трудно, ибо для этого требуется богатое воображение.
Недаром в истории теории управления зафиксировано совсем немного
подобных откровений. В результате теория управления содержит, по

320 Заключение
сути дела, протоколы решения стандартных задач, тогда как жела-
тельно иметь правила синтеза, распространяемые на новые ситуации.
В монографии впервые предпринята попытка развития гипотезы
о структуре механизма формирования обратной связи. Эта гипотеза
базируется на "иерархии" сложности обратной связи. Подобное пред-
ставление о структуре обратной связи кажется вполне естественным,
ибо позволяет свести проблему синтеза сложного нелинейного регуля-
тора к решению последовательности однотипных и хорошо изученных
задач. Иначе говоря, видимая сложность проблемы рекуррентно по-
рождается невидимой внутренней простотой.
Для реализации принципа иерархии потребовалось введение нового
для теории управления понятия сигнала-оператора. Этот термин от-
ражает двойственную природу сигналов в нелинейных динамических
системах. В сочетании с принципом обратной связи сигнал-оператор
предоставляет необходимые возможности для перехода от непосред-
ственного решения задачи к нахождению сначала г1Лгоритма решения
задачи, а если потребуется, то и к гшгоритму, определяющему ал-
горитм решения задачи, и т.д. Получаемая таким образом "иерар-
хическая структура" обратной связи примечательна еще и тем, что
на каждом иерархическом уровне управляющие механизмы просты,
однотипны и могут быть получены стандартными для классической
теории регулирования способами.
Обратим внимание читателя на то, что идея о двойственной при-
роде переменных величин обычна для естествознания и весьма плодо-
творна. Так, например, Макс Борн ввел понятие оператора физиче-
ской величины, которое оказалось очень продуктивным в квантовой
механике, имеющей дело с объектами дуальными в первооснове, а по-
нятие оператора-времени, введенное Ильей Пригожиным, оказалось
очень полезным в физике необратимых процессов.
Авторы уверены, что появление принципа бинарности и новых ти-
пов обратных связей довольно естественно для современного этапа
развития общей теории обратной связи. Для обоснования этого те-
зиса авторы подробно рассмотрели эволюцию важнейших принципов
и методов теории регулирования по мере роста факторов неопреде-
ленности в задачах управления, что представляет самостоятельный
интерес и может служить кратким введением в классическую теорию
обратной связи.
Заметим также, что с математической точки зрения предложен-
ный подход можно рассматривать как способ синтеза нелинейных ди-
намических систем с заранее предписанными свойствами их решений,
такими, например, как устойчивость, малая чувствительность по от-
ношению к вариациям параметров задачи и т.п. Разумеется, приме-
