Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

9.2.

Следящие

дифференцирующие

системы

271

Кроме того, нетрудно заметить, что структурная схема диффе-

ренциатора первой разности

~^_9it)-9(t-h)

^~ h

имеет вид, показанный на рис. 9.14, и содержит звено запаздывания,

реализация которого — также непростое дело. Передаточная функ-

ция дифференциатора (9.10) находится из рис. 9.14 и дается выраже-

-»•

-гЬ»

Рис. 9.14

нием Wois) = Л/(1

—

е~ ). При малых значениях |Лв| справедливо

разложение l-e"*' = As— (Л'/2) в^-|-0(|Лв|^), поэтому WD(S) можно

приближенно аппроксимировать выражением

WD{S)

Л 2 Л Л \ 8

(h/2)8-

Иными словами, если обозначить Т = Л/2, то передаточная функ-

ция такого дифференциатора близка к передаточной функции RC-

цепочки Wj){s) ^ s/{Ts+l), следовательно, их свойства также близки.

Поэтому не будем повторяться и перейдем к "следящим" дифферен-

циаторам.

9.2.

Следящие дифференцирующие системы

Структурный принцип построения дифференциаторов рассматривае-

мого типа отражает рис. 9.15, на котором Fout — выходной фильтр, а

Ry — регулятор, стабилизирукшщй в нуле ошибку слежения е = g

—

^ е

I'out

Рис. 9.15

272

Глава 9. Диффереицирование сигналов

В случае, когда сигналы g{t) и z{t) гладкие, из равенств е = О, i = у

немедленно получаем требуемое у = д. Если же z(t) не имеет обыч-

ной производной, то с помощью фильтра Fout можно сформировать

требуемую оценку производной

9 = Fouty-

Таким образом, задача дифференцирования может быть сформу-

лирована как задача слежения и возникающие при этом варианты

определяются выбором пары {Ry,Foxit}- Рак:смотрим некоторые из

них.

9.2.1.

Линейный дифференциатор

Простейшим следящим дифференциатором можно считать линейный

дифференциатор, для которого

{Ry, Fout} = {к, 1}, к = const > 0.

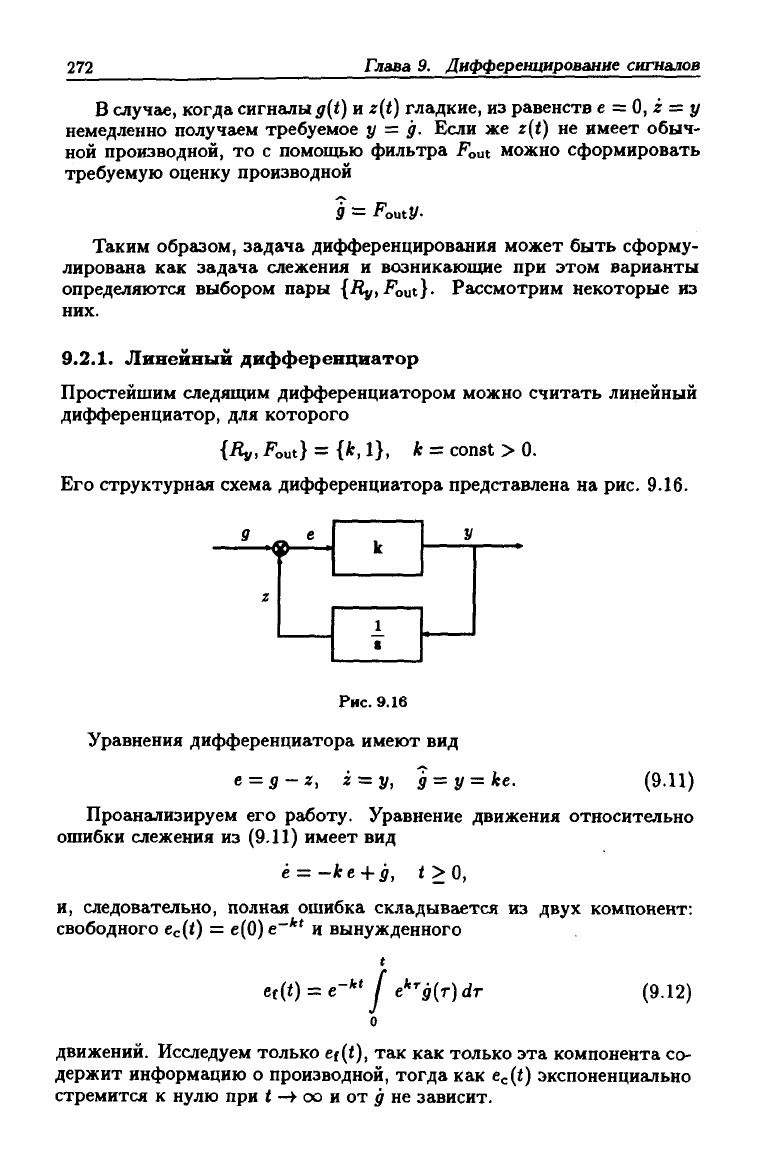
Его структурнг1Я схема дифференциатора представлена на рис. 9.16.

Рис. 9.16

Уравнения дифференциатора имеют вид

e = g-z, z = y, д = у = ке.

(9.11)

Проанализируем его работу. Уравнение движения относительно

ошибки слежения из (9.11) имеет вид

ё = -ке

д,

t>0,

и, следовательно, полная ошибка складывается из двух компонент:

свободного ес(<) = е(0) е~** и вынужденного

et{t)

=.€-"'

e>'-g{T)dT

(9.12)

движений. Исследуем только

et{t),

так как только эта компонента со-

держит информацию о производной, тогда как edt) экспоненциально

стремится к нулю при

< —>

оо и от ^ не зависит.

9.2.

Следящие

дифференцирующие

системы

273

Пусть д

—

const, тогда (9.12) легко интегрируется и

e,(0 = f(l-e-*').

Поскольку у = ке, то для оценки производной имеем формулу

Ьл(1-е-*0.

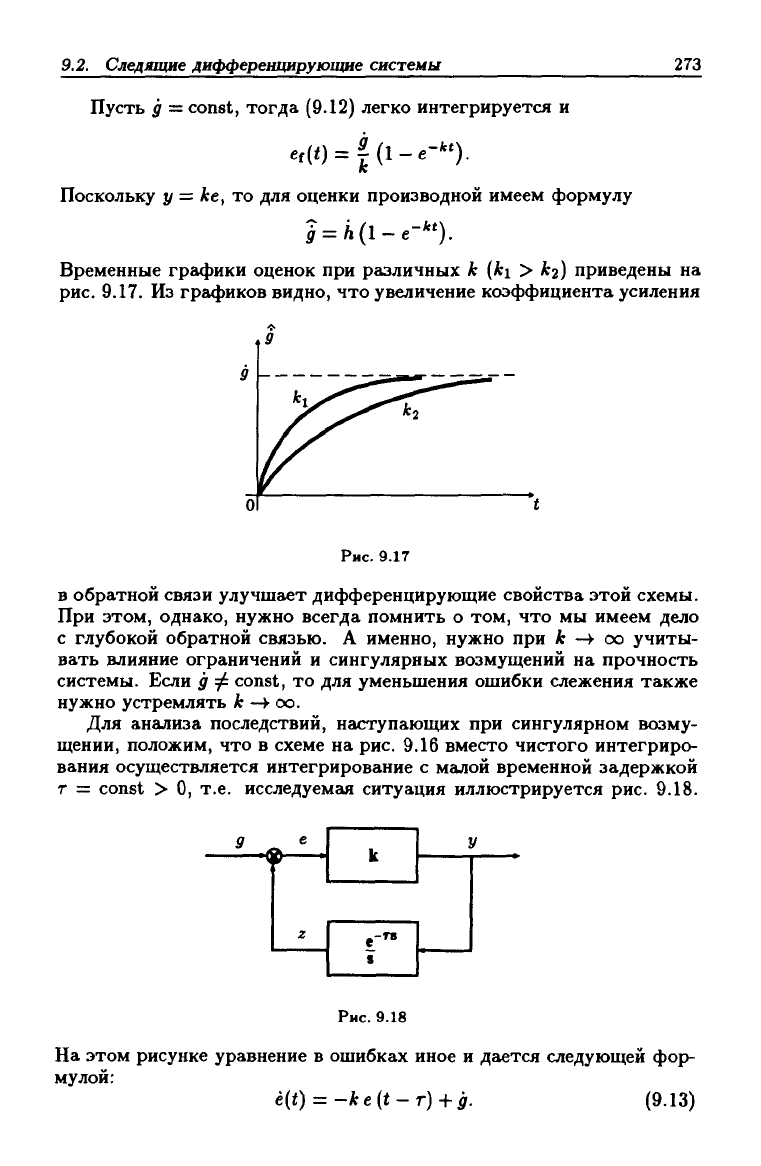
Временные графики оценок при различных к {ki > /fj) приведены на

рис.

9.17. Из графиков видно, что увеличение коэффициента усиления

Рис. 9.17

в обратной связи улучшает дифференцирующие свойства этой схемы.

При этом, однако, нужно всегда помнить о том, что мы имеем дело

с глубокой обратной связью. А именно, нужно при к

—¥

оо учиты-

вать влияние ограничений и сингулярных возмущений на прочность

системы. Если д ф const, то для уменьшения ошибки слежения также

нужно устремлять fe -> оо.

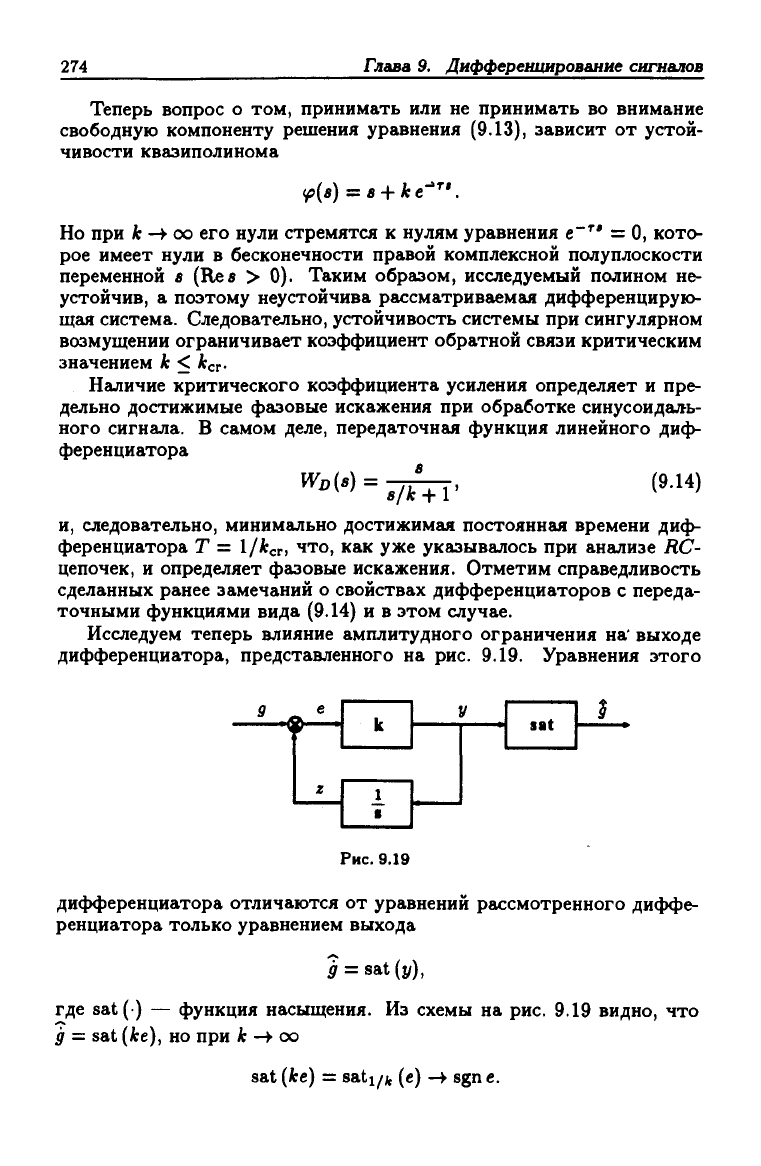
Для анализа последствий, наступающих при сингулярном возму-

щении, положим, что в схеме на рис. 9.16 вместо чистого интегриро-

вания осуществляется интегрирование с малой временной задержкой

г = const > О, т.е. исследуемая ситуация иллюстрируется рис. 9.18.

9 ,

Рис. 9.18

' !/

На этом рисунке уравнение в ошибках иное и дается следующей фор-

мулой:

'e{t) = -kt{t-T)^g. (9.13)

274

Глава

Диффереицирование сигналов

Теперь вопрос о том, принимать или не принимать во внимание

свободную компоненту решения уравнения (9.13), зависит от устой-

чивости квазиполинома

<р(8)

+ ке^^'.

Но при

->•

оо его нули стремятся к нулям уравнения е"'"' =

О,

кото-

рое имеет нули в бесконечности правой комплексной полуплоскости

переменной s (Res > 0). Таким образом, исследуемый полином не-

устойчив, а поэтому неустойчива рассматриваемая дифференцирую-

щая система. Следовательно, устойчивость системы при сингулярном

возмущении ограничивает коэффициент обратной связи критическим

значением к <

ксг-

Наличие критического коэффициента усиления определяет и пре-

дельно достижимые фазовые искажения при обработке синусоидаль-

ного сигнала. В самом деле, передаточная функция линейного диф-

ференциатора

^-W

Jjrrv

(^•^^^

и, следовательно, минимально достижимая постоянная времени диф-

ференциатора Т =

1/Агсг,

что, как уже указывалось при анализе RC-

цепочек, и определяет фазовые искажения. Отметим справедливость

сделанных ранее замечаний о свойствах дифференциаторов с переда-

точными функциями вида (9.14) и в этом случае.

Исследуем теперь влияние амплитудного ограничения на' выходе

дифференциатора, представленного на рис. 9.19. Уравнения этого

sat

Рис. 9.19

дифференциатора отличаются от уравнений рассмотренного диффе-

ренциатора только уравнением выхода

J = sat (у),

где sat() — функция насыщения. Из схемы на рис. 9.19 видно, что

д = sat (ке), но при к -> оо

sat

{ке)

= sati/fc (е) -> sgne.

9.2.

Следящие дифференцирующие системы

275

Таким образом, в пределе, при к -¥ оо, наличие ограничения при-

водит к разрывному сигналу (рис. 9.20). Поэтому для получения при-

sat^^

(е)

fc — 00

eatj^^

(е)

Рис. 9.20

емлемой оценки неизбежно использование выходного фильтра Fout<

надлежащим образом "усредняющего" разрывной сигнал sgny и не-

избежно вносящего дополнительные фазовые искажения (рис. 9.21).

9 '

-1

Fout

Рис. 9.21

Рис. 9.22

sat

Далее методы усреднения исследуются подробно, здесь же огра-

ничимся замечанием, что к исходным проблемам приводит наличие

амплитудного ограничения в замкнутом контуре (рис. 9.22), когда

предельный переход

А;

—^

оо приводит к релейному дифференциатору.

К анализу свойств релейного дифференциатора теперь и переходим.

276

Глава 9. Дифференцирование сигналов

9.2.2. Релейный дифференциатор

Структура релейного дифференциатора, характеризующегося парой

{Ry, Fout] = I * sgn e, —7j \

изображена на рис. 9.23. За оценку сигнала примем выход системы,

т.е.

положим д = X. Для анализа процессов в замкнутом контуре

^ .й

-к

! t

Ts+1

рис. 9.23

запишем уравнение движения относительно ошибки с:

ё = -ksgn е + д,

которое легко получается из уравнений дифференциатора

e—g

—

= fcsgne,

А:

= const > О,

i = I/, Тх + х = у, Т = const > 0.

(9.15)

(9.16)

Видим, что если к > |^|, то за конечное время процесс стабили-

зируется в нуле е = О, где возникает скользящий режим (рис. 9.24).

Рис. 9.24

в скользящем режиме среднее значение разрывного сигнала находится

из равенств е = О, ё =

и дается выражением Arsgngq е = д. Для выде-

ления этого среднего и нужен выходной фильтр.

9.2. Следящие дифференцирующие системы

277

Действительно, из (9.16) и (9.15) имеем уравнение фильтра

Тх + х = д-ё,

вынужденнее компонента решения которого дается хорошо известной

формулой

x,(t)

= ^е-Ч^ J e^'^{9(r) - ё{г)) dr. (9.17)

Пусть существует и равномерно ограничена вторе1Я производная

сигнала д, т.е.

< М, М = const > О, (9.18)

а скользящий режим возник при / = О, тогда справедлива следующая

цепочка равенств:

/ е^/'Гё(г) dT = j е^/^ rfe(r) =

= е(г)е^/^

* t

(9.19)

/e(r)e-/^d(r/r)=0.

Следовательно, (9.17) можно упростить до выражения

(9.20)

для дальнейшего преобразования которого вновь воспользуемся инте-

грированием по частям. В результате имеем

je^l'^ad{rlT)=iade^l'^=ge^l'^

о о

- / e'lTg dT = g е^/^ - д(0) - / е^/^ д dr.

(9.21)

Последнее слагаемое в этой формуле оценивается с учетом (9.18) сле-

дующим образом:

j e'/'^gdr

<Je^''^\g\dT<

< M/e^/^dr = TM(e*/^-l).

После подстановки (9.21) в (9.20) находим, что

(9.22)

Xfit) = g{t) - д{0) е-'/^ - е"^ J е^'^д dr = g{t) + e{t). (9.23)

278

Глава 9. Дифференцироваиие сигналов

Для погрешности дифференцирования £{t) из (9.22) и неравенства

1^(0)

< к имеем оценку

\е{1)\<ТМ + (к + ТМ)е-*'^. (9.24)

Таким образом, окончательно получаем

\x{(t)-g(t)\<TM + (k + TM)e-*'^.

(9.25)

Для уменьшения регулярной {ТМ} и асимптотически исчезающей

{ (fc + ТМ) е~*1^ } компонент погрешности дифференцирования, как

видно из (9.25), следует уменьшать постоянную времени Т фильтра, и

в пределе при Т =

получим абсолютно точное дифференцирование.

Но это физически недостижимо, и причина в том, что переключения

всегда неидеальны и выбор параметра Т должен быть согласован с

этими неидеальностями.

Пусть, например, имеется пространственная задержка Д = const

в переключениях (рис. 9.25). Тогда для описания дифференциатора с

\Ъ

Т$+1

Рис.

9.25

неидеальными переключениями справедливы все уравнения релейного

дифференциатора со схемы на рис. 9.23 при замене в них идеального

реле на реле с гистерезисом sgпд е, в частности, имеем следующее

уравнение в ошибках:

ё = -ksga^e-irg.

В окрестности |е| < А возникает реальный скользящий режим

(рис.

9.26). Справедлива также оценка для погрешности (9.24), вно-

Реальнын скользящий

режим

Рис.

9.26

9.2.

Следящие

дифференцирующие системы

279

симая динамикой фильтра, однако теперь

\e{t)\

< А и оценка (9.22) не

имеет места. Используя выражение из (9.22), находим оценку, при-

годную для этого случая. Имеем

1/'

,т/Т

г(<)

e(t) еЧ'^ - е(0) | + 0| e{t)

{е"'^ - 1) < 2Д (е""^ - 1).

После подстановки найденной оценки, (9.23) и (9.24) в (9.17), устана-

вливаем справедливость оценки погрешности дифференцирования:

2А / 2А

\xf{t)-g{t)\<TM^--+(k + TM^ —

)е'/^

(9.26)

Теперь видно, что при Т ->

погрешность не уменьшается, как ожи-

далось, а напротив, увеличивается.

Точность дифференцирования действительно будет повышаться,

если имеет место условие

• • Д п

hm -= = 0.

т->о Т

С физической точки зрения последнее соотношение означает (9.26),

что высокочастотная составляющая сигнала y(t) действительно от-

фильтрована и выделена только полезная составляющая д. Проведен-

ное исследование показало, что

• в релейном дифференциаторе невозможно выбором единственного

параметра Т одновременно уменьшить погрешности, вносимые ди-

намикой фильтра {ТМ) и неидеальностями переключений (А/Т).

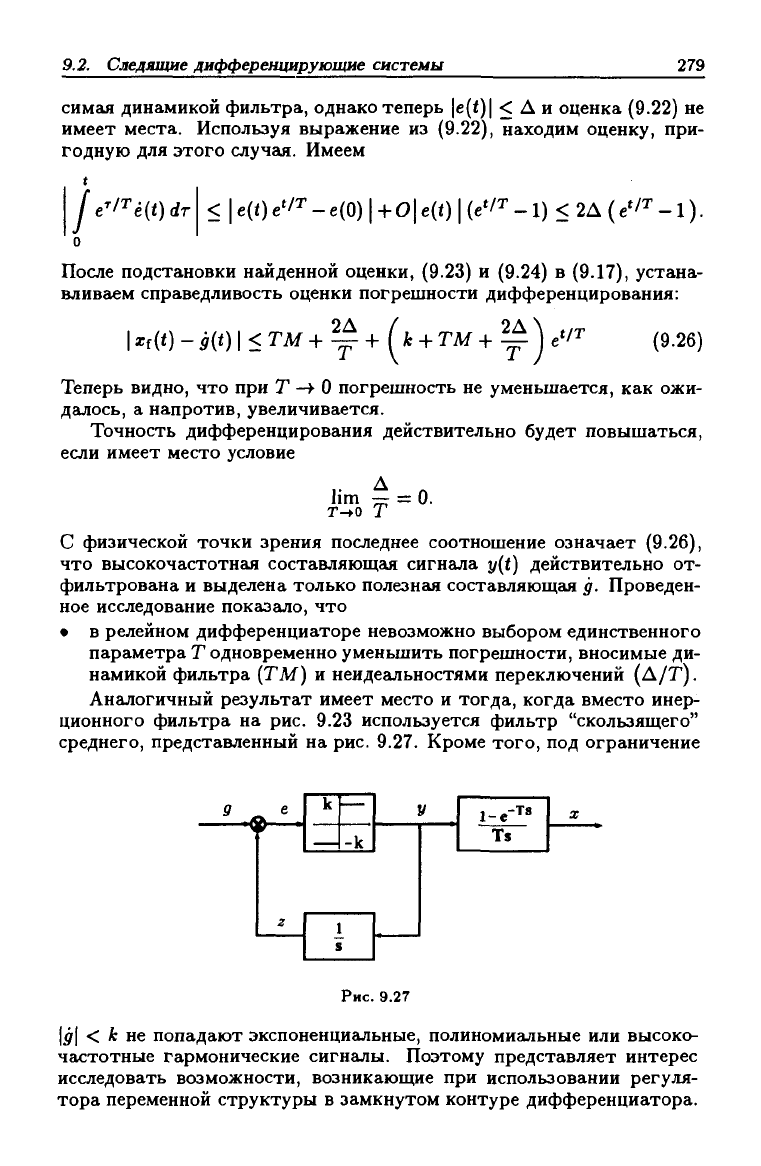
Ангшогичный результат имеет место и тогда, когда вместо инерь

ционного фильтра на рис. 9.23 используется фильтр "скользящего"

среднего, представленный на рис. 9.27. Кроме того, под ограничение

-к

Рис. 9.27

1^1 <

А;

не попадают экспоненциальные, полиномиальные или высоко-

частотные гармонические сигналы. Поэтому представляет интерес

исследовать возможности, возникающие при использовании регуля-

тора переменной структуры в замкнутом контуре дифференциатора.

280

Глава 9. Дифференцирование сигналов

9.2.3.

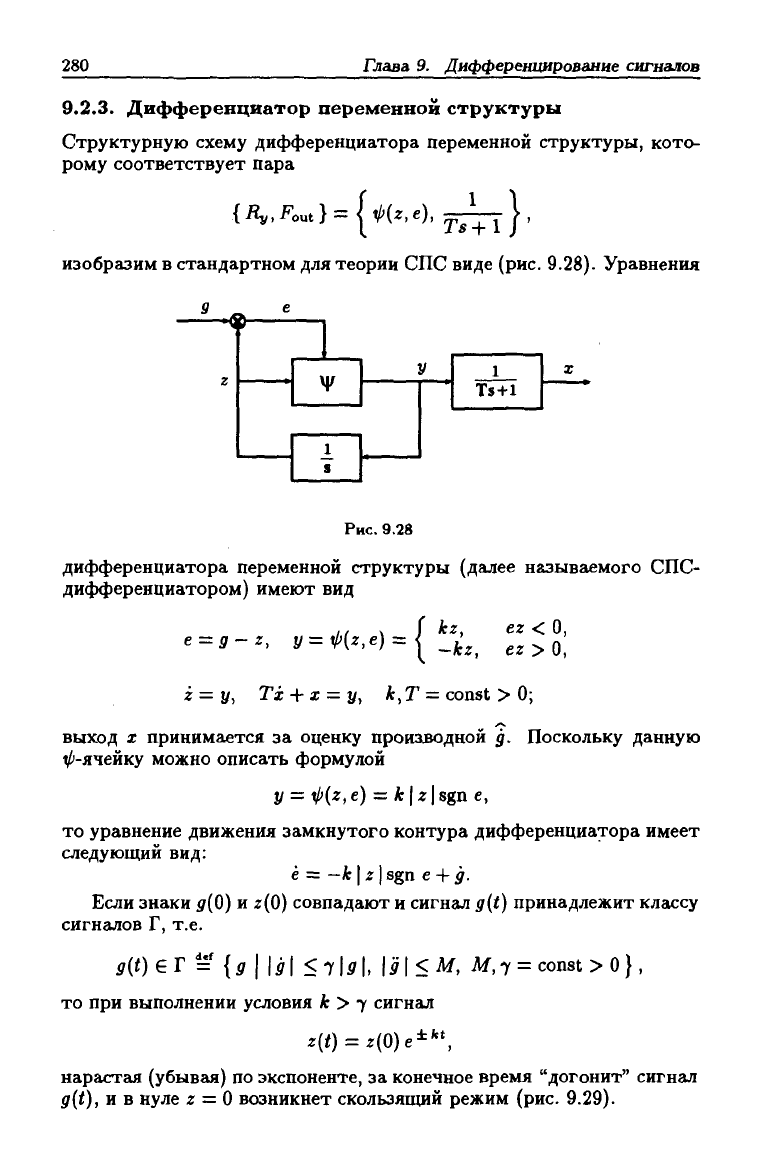
Дифференциатор переменной структуры

Структурную схему дифференциатора переменной структуры, кото-

рому соответствует пара

изобразим в стандартном для теории СПС виде (рис. 9.28). Уравнения

•Ф

Ts+l

Рис. 9.28

дифференциатора переменной структуры (далее называемого СПС-

дифференциатором) имеют вид

// \ f кг, ez <

e=a-z, y=i>(z,e) = i^ _^^_ ^^^

Z = у, Тх

-{•

X = у, к,Т = const > 0;

выход X принимается за оценку производной д. Поскольку данную

^-ячейку можно описать формулой

у = ipiz, e) = k\z\sgne,

то уравнение движения замкнутого контура дифференциатора имеет

следующий вид:

ё = -*г

sgn е

-I-

Если знаки д{0) и z(0) совпадают и сигнал g{t) принадлежит классу

сигналов Г, т.е.

9{t)£T= {д\ \д\ <7|д|,

\9\<М,

М,7 = const >

О }

то при выполнении условия к > у сигнал

нарастая (убывая) по экспоненте, за конечное время "догонит" сигнал

g{t),

и в нуле z =

возникнет скользящий режим (рис. 9.29).