Емельянов С.В. Новые типы обратной связи

Подождите немного. Документ загружается.

8.1.

Ограничения

операторной

переменной

251

Отметим, что при использовании инерционно-релейного КО-регуля-

тора qji = Ьц

—

к sgn ^ ограничение |/i| < const выполнено автома-

тически. Если же, однако, используется обычное инерционное звено

qii = bn

—

к^, то ограничитель выхода необходим.

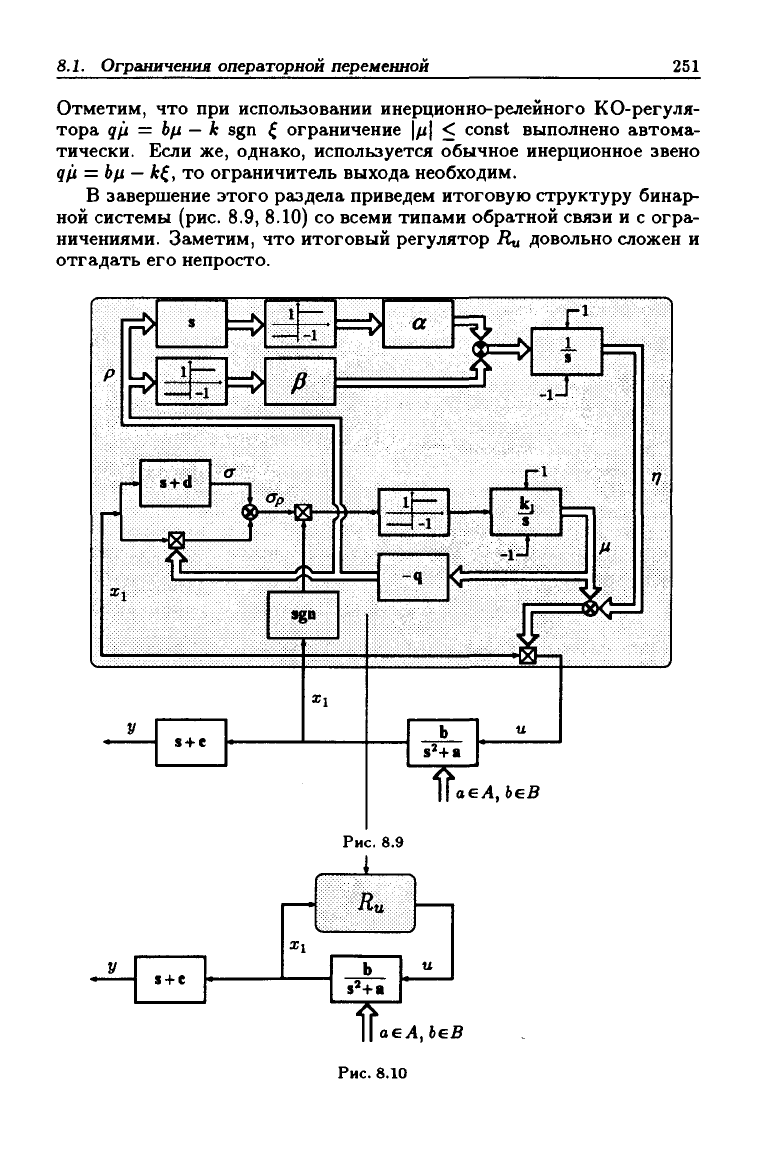
В завершение этого раздела приведем итоговую структуру бинар-

ной системы (рис. 8.9, 8.10) со всеми типами обратной связи и с огра-

ничениями. Заметим, что итоговый регулятор Л„ довольно сложен и

отгадать его непросто.

4т^=^

i + d

|]^^^ч|н|->[^

sgn

•ч С

ТТ

«<Й

S + C

s'+«

if а 6

л,

беВ

Рис.

8.9

, ^ ,

S + C

Х\

Д-И

1ГаеЛ,

б€В

Рис.

8.10

252

Глава 8. Ограничения, физические основы компенсации

8.2. О глобальном поведении бинарной системы

В данном разделе ответим, наконец, на первый из поставленных в на-

чале этой главы вопросов, а именно на вопрос об уравнениях движе-

ния и свойствах синтезированной бинарной системы при произволь-

ных начальных условиях по х, т.е. в том числе и не принадлежащих

\ -

Рис.

8.11

множеству Gs (рис. 8.11). Рассмотрим для определенности бинарную

систему с К- и КО-связями вида

и = кцХ1, /i =-A;isgn[^-|-/z|^|].

(8.9)

Если использованы, кроме того, другие типы обратной связи, то со-

ответствующее исследование даже проще предлагаемого.

Из (8.9) следует, что переменные

(л

и и ограничены:

Ы<1> M<fc|a;i|.

Более того, если действие уравнений (8.9) распространить за пределы

множества Gs, а для этого достаточно вместо стандартного

положить

тогда при нахождении фазовой точки вне Gs переменная fx через про-

межуток времени, меньший 2/ki, принимает следующее значение:

/i = -sgn

(axi).

(8.10)

После подстановки (8.10) в первое из соотношений (8.9) находим, что

управление принимает форму и =

—k\xi\sgn(T,

совпадающую с обрат-

ной связью СПС. А раз так, то и фазовые траектории те же самые,

что в СПС.

8.2. О глобальном поведении бинарной

системы

253

Таким образом, если в СПС параметр к выбран так, что имеет

место попадание на линию разрыва <г = О, то в бинарной системе

это также имеет место, т.е. множество Gs является притягивающим

множеством. Необходимым и достаточным условием попадания явля-

ется отсутствие вещественных положительных нулей у характеристи-

ческого полинома системы

XI = Х2,

Х2 = axi

—

bkxi

при любых фиксированных а Е А, Ь ^ В. Последнее, очевидно, спра-

ведливо, когда

кЬ-

> а°. (8.11)

Таким образом, при выполнении условия (8.11) множество Gg при-

тягивающее. Если побеспокоиться о том, чтобы оно было также ин-

вариантным (т.е. все начинающиеся в нем движения не должны поки-

дать его в дальнейшем), то Gs было бы аттрактором и весь ан£1лиз из

предшествующих глав без изъятий годился бы для исследования та-

кой ситуации. Но в рассматриваемой бинарной системе (К-|-КО-связи)

множество Gs является не аттрактором, а только условно инвариант-

ным множеством. Именно, если внутри Gs можно указать множество,

например, той же конфигурации Gs'

{О

< S' < 5) такое, что движения,

начинающиеся в Gs', не покидают Gs, то последнее — условно инва-

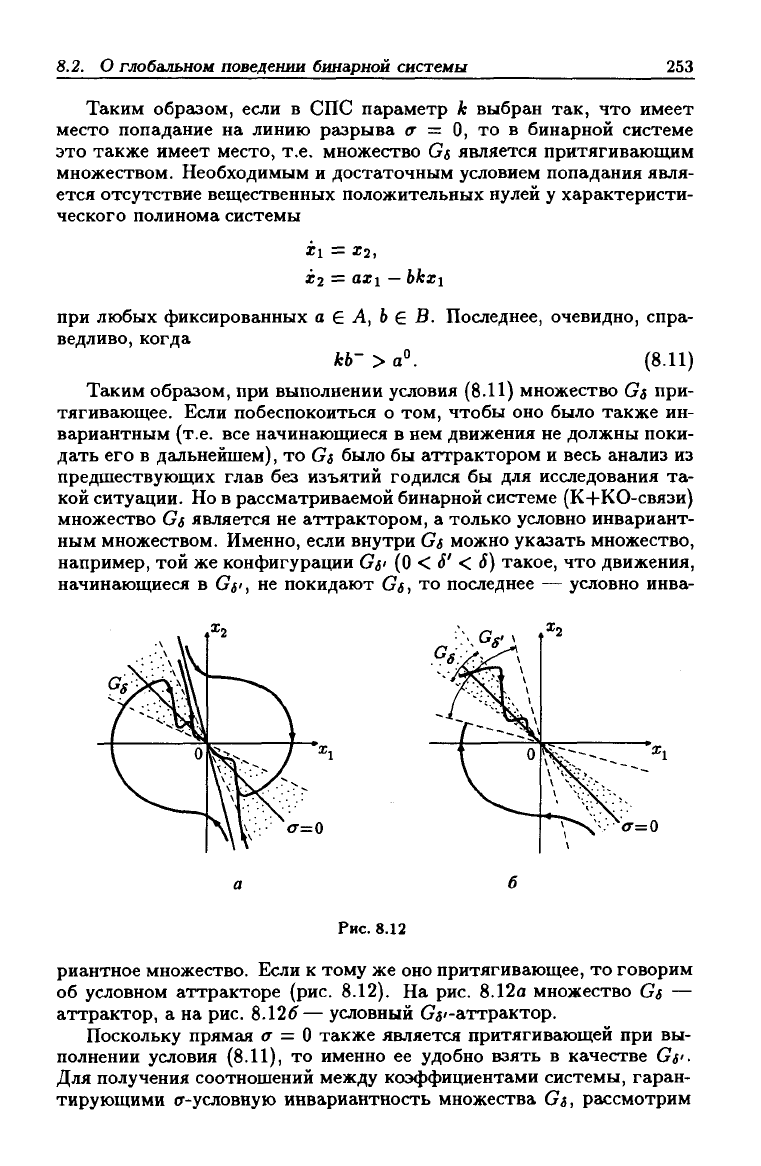
Рис.

8.12

риантное множество. Если к тому же оно притягивающее, то говорим

об условном аттракторе (рис. 8.12). На рис. 8.12а множество Gs —

аттрактор, а на рис. 8.125— условный О^'-аттрактор.

Поскольку прямая «г =

также является притягивающей при вы-

полнении условия (8.11), то именно ее удобно взять в качестве Gs'.

Для получения соотношений между коэффициентами системы, гаран-

тирующими (Т-условную инвариантность множества Gs, рассмотрим

254

Глава

Ограничения,

физические основы компенсации

следующее известное по предыдущим главам уравнение движения от-

носительно переменной ^ =

<T/XI

^ =

2d^

kbfi

+ a,,

a,=a-d^,

Jfc

= const, (8.12)

и уравнение КО-регулятора

/i = -Arisgn({-|-/i|^|), ^1= const.

Ясно,

что множество

является <т-условно инвариантным, если вся-

кое движение, стартовавшее с линии а = 0 (т.е. при ^ = 0), не достиг-

нет границы Gs (т.е. |^| = J).

Из (8.12) имеем в Gf оценку

\i\<2dS +

a°

kb+,

a° = a°-d\

поэтому за время t переменная ^ "нарастет" не более чем на величину

\^\<(2dS

a° + kb+)t.

Из требуемого условия |^| <

получаем следующую оценку на

время "нарастания":

' ^ 2dJT^TIF- (8-^3)

Но рост гарантированно прекратится тогда, когда переменная /i до-

стигает крайнего значения fi = —sgn^ прежде, чем переменная |^|

достигнет значения S и, кроме того, будет выполнено неравенство

2dS

- kb- +а°<0, а° = а°- d^. (8.14)

Максимальное время, необходимое для изменения переменной fi

от одного крайнего значения до другого, меньше 2/ki. Поэтому из

последнего неравенства и (8.13) получаем следуюпдую окончательную

оценку для расчета параметра ki:

ki>^{2dS + a° + kb+), (8.15)

где параметр к определяется из (8.14) неравенством

,>!^.

,8.16)

Соотношения (8.15), (8.16) полностью определяют параметры К- и

КО-связей, так как (8.16) гарантирует притяжение для прямой

<г

= 0.

Заметим также, что при использовании 0-связи нижнюю оценку ко-

эффициента ki можно уменьшить вдвое.

8.2. Физические основы компенсащш неопределенности 255

8.3.

Физические основы

компенсации неопределенности

Перейдем теперь к ответу на третий вопрос о физических основах

компенсации неопределенности.

Прежде всего отметим тот очевидный факт, что всякое возмуще-

ние можно трактовать как некую силу, влияние которой компенсиру-

ется только другой, эквивалентной ей силой. Например, при прямой

компенсации возмущения / в управлении

= da + Ьи-^ f

управление формируется в виде суммы

где компонента uj = —f/b является компенсирующей силой, а компо-

нента

— стабилизирующей.

При неизвестном возмущении / можно использовать большой ко-

эффициент усиления в обратной связи и =

—кег,

тогда в замкнутой

системе, описываемой уравнением

г=-(''"^)"-'р

компенсация достигается при к -^ оо, когда приведенное возмущение

(f/k) -^ 0. В этом случае компенсирующая сила образуется в резуль-

тате умножения большого к на малый сигнал (т.

Релейное управление

и =

—«"

sgn

or,

и° = const

также "силовым" способом подавляет действие возмущения /:

d(r —

и°Ь

sgn <т

+ f,

которое теперь, однако, должно быть равномерно ограничено:

1/1

< «°.

При этом в нуле переменной

<т

существует скользящий режим и сред-

нее значение разрывного сигнала с точностью до знака совпадает с

компонентой u/ в методе прямой компенсации

и°

sgn^

(т

= f/b.

Таким образом, во всех указанных случаях

• идея силовой компенсации возмущения реализуется с помощью от-

рицательной обратной связи.

256 Глава 8. Ограничения, физические основы компенсации

В бинарных системах (и в СПС, конечно, тоже) компенсация до-

стигается иными средствами. Действительно, в этом случгш

и = k^xi,

и произведение к/л = Jt^, играет роль коэффициента передачи обратной

связи. Но при использовании релейного КО-регулятора

/^ = -sgn^

или интегрально-релейного КО-регулятора

/i = -kisgn

{сг

+ ц\а\)

переменная /л меняется от —1 до -1-1 и, значит, коэффициент обрат-

ной связи главного контура к^ также меняет знак. Последнее озна-

чает, что в главном контуре используется знакопеременнгш обратная

связь и поведение системы описывается Е"'"-уравнениями:

XI = Х2,

Х2 = axi + kbxi,

или S -уравнениями:

Xi = Х2,

Х2 = axi

—

kbxi.

Поскольку кЬ > а°, то Е"*"-система всегда неустойчива, и это прин-

ципиальный момент. Именно:

• использование неустойчивых структур позволяет в системе с огра-

ниченными параметрами за конечное время увеличить норму фа-

зового вектора до величины, достаточной для подавления возму-

щения.

Как мы теперь знаем, использование для этого разрывной обратной

связи вовсе не является неотвратимым, годятся любые, необязательно

линейные, законы управления, меняющие знак обратной, связи.

8.4. О компенсации координатного возмущения

Рассмотрим теперь способ решения четвертой задачи, поставленной

в начале главы, — задачи об алгоритмах стабилизации вынужденного

движения.

До сих пор, по уговору, предполагалось, что /(<) = 0. Пусть теперь

это не так, а именно, в уравнении изменения ошибки КО-контура а

имеется дополнительный аддитивный член, т.е.

& =

d(r

+ bu + a'xi + f,

a'=a-d^,

b Е В, а е А.

8.4. О компенсяции координатного возмущения 257

Наличие слагаемого f(t) в правой части качественно меняет ситу-

ацию.

Поскольку возмущение f{t) предполагается известным с точ-

ностью до включения

/е^={/11/1</м},

где,

кроме того, неизвестен и параметр 6 € S, то оно не может быть

включено в параметрическое возмущение или устранено с помощью

известных методов компенсации: прямым или косвенным измерением.

Поэтому актуален вопрос об изменениях, которые следует внести в

конструкцию бинарных систем управления, с тем чтобы наделить их

свойством стабилизируемости при координатном возмущении.

Заметим, что при неизвестном b Е В проблема остается нерешен-

ной даже при известном f{t), поскольку стандартные методы стабили-

зации в такой ситуации неприменимы. Если известна волновая модель

возмущения /, т.е. известен аннулирующий его оператор Kf:

Kjf = О,

то заменой управления

u=KJ^v

задача стабилизации вынужденного движения сводится к стабилиза-

ции свободных колебаний, так как

& =

dtT

+ bKJ^

+ a*xi -f- /,

и после введения новых переменных

^ = Kf

(Г,

XI = К/

получаем стандартную задачу стабилизации

а = da + bv + a*xi,

В этих выкладках для простоты и без потери общности полагалось,

что b = const. Таким образом,

• наиболее общая и трудная ситуация возникает тогда, когда о воз-

мущении /(<) известен только факт включения f £ F,& параметры

объекта неизвестны, т.е. а Е А, b € В.

Именно этой ситуацией далее и займемся.

Пусть координатное возмущение удовлетворяет МС-условию. То-

гда с помощью стандартной замены переменного

сводим исходную задачу стабилизации объекта Р:

XI = 12.

Х2 = axi +bu + f

258 Глава 8.

Ограничения,

физические основы

компенсации

к задаче стабилизации скалярного объекта Ро:

& = d<r+

Ьи

+ a,xi + f, а, = а

—

d^.

Как обычно, при управлении вынужденным движением выберем

управление в виде суммы

ti = u,+ U/, (8.17)

где компонента Ux стабилизирует свободные колебания объекта Pi:

а =

diT

bux

+ a,xi,

а компонента и/ стабилизирует вынужденные колебания объекта Pj:

а = buj + /.

Как и ранее, предполагается, что

Л, 6 6 5, / € F.

При использовании разрывных управлений из стабилизации Рх и

Рг-объектов следует стабилизация Р<,-объекта, В самом деле, разрыв-

ные стабилизирующие управления «,, u/, очевидно, удовлетворяют

условиям

cr(d<T-|-bux + a.xi) <0, (8.18)

<r{buj

+ /) < 0. (8.19)

Поскольку это так, то и их сумма удовлетворяет аналогичному усло-

вию

(T{da

+ 6(«,

-I-

U/)

-I-

а.ц -f- /) < О,

которое эквивалентно неравенству

<Tff<0,

влекущему за собой стабилизацию Р,-объекта в нуле.

Законы управления, разрешающие неравенства (8.18), (8.19) при

любых а ^ А,

^ В

тл

f ^ F, очевидно, имеют вид

ы, = -*|ari|sgn<7-, (8.20)

u/ = -//MSgn<T, (8.21)

где константы к, I удовлетворяют соотношениям

kb->a° = a° +

d^,

, ^

,ь-

> 1.

(«•^^'

Алгоритмы управления (8.20), (8.21) стандартны для теории СПС.

При переходе от разрывных алгоритмов стабилизации к непрерыв-

ным можно поступить следующим образом. Используя стандартные

обозначения

fi = -sgn (xia) = -sgn i, ^ = (г/ii, (8.23)

8.4.

О компенсации координатного возмущения

259

алгоритмы стабилизации управления (8.20), (8.21) можно записать в

виде

« = «с + «/ =

(Jtxx

+ //м sgn

xi)/i.

(8.24)

Возьмем теперь формулу (8.24) при синтезе непрерывного закона

за основу, но вместо релейного КО-регулятора применим, к примеру,

интегрально-релейный КО-регулятор

/i = -*?8gn(^ + /iK|), (8.25)

где к\, как будет видно далее, уже не коэффициент, а некоторая функ-

ция, зависящая от фазового вектора и мажоранты возмущения.

Для нахождения этой функции к\, гарантирующей «т-условную ин-

вариантность множества Gt, т.е. выполнение неравенства |^| < 6,

если ^(0) = О, воспользуемся уравнением изменения 0-переменной ^

в множестве Gt. Это уравнение выводится стандартным образом и

имеет следующий вид:

Xi Xi

Поскольку, согласно (8.24),

то искомое уравнение окончательно можно записать в виде

i=2d^

b(h

^P^\n

a,-{-^-^.

(8.26)

\ Fi| / Xi

Из (8.24) имеем

1/^1

< 1, следовательно, для правой части уравнения

(8.26) в Gt верна оценка

/м

l^|<2.,+**(.

iZ«)

+ .; +

За время t переменная ^ возрастает с нуля (^(0) = 0) не более чем

на величину |^тах| {х\ можно считать постоянной, так как движение

происходит в Gf, а J и f малы), где

|чтах| —

2(fJ-|-6+Jfc + a2 + ^^f^i/Af

Fil

t. (8.27)

Полученная величина не превысит допустимый предел

если за

время t, согласно (8.22), 0-переменная ц гарантированно примет зна-

чение // = —sgn^. Но это может быть только тогда, когда

t > 2/к°. (8.28)

260

Глава 8. Ограничения, физические основы компенсации

Из соотношений (8.27), (8.28) и неравенства |^тах| < ^ получаем

оценку снизу для функции к\:

kl>

(8.29)

Из полученной оценки следует, что функция к° отличается от кон-

станты ki, действующей при управлении свободным движением, на

слагаемое

2(6+/ + 1)

6\хг\

обусловленное наличием внешней силы /. При отсутствии этой силы

(/м = 0) данная оценка совпадает с ранее установленной.

Второй вывод из (8.29) тот, что в окрестности нуля переменной Рх

функция к\ неограниченно возрастает, что неприемлемо. Для огра-

ничения этой функции вместо (8.29) следует использовать оценку

*?>*!

+ ^^fM =

кг

+ k'jM,

(8.30)

где Д — положительная константа, определяющая размер шара дис-

сипативности

Br{0)={x\xl + xl<r^{A)).

Последнее замечание о диссипативности системы обусловлено тем,

что при ограниченной функции к^ из (8.30) при малых xi (\xi\ < Д)

проекции фазовых траекторий системы на множество Gs могут по-

кинуть это множество, чего не может быть для функции к^ из (8.29).

Поэтому условие (8.30) гарантирует стабилизацию всех решений (ра-

зумеется, при выполнении условий притяжения для G;) в окрестности

нуля, погруженной в шар Вг(0) (рис. 8.13). Отметим, что при Д ->

Рис. 8.13