Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour
Подождите немного. Документ загружается.

and transmit pressure waves to an extent dependent upon the charac-
teristics of the particular hydraulic element. As a general rule other
pipeline features such as tanks and reservoirs, blank flanges, changes
of pipe properties and bifurcations for instance all act passively to
reflect and/or transmit pressure waves. A rare exception to this rule
might be where surface waves introduce pressure and flow variations
at the inlet of a submerged pipe.
Other boundaries such as air-valves, pressure-relief valves and check
valves respond to changing flow conditions and may only come into play
at certain stages of a transient event. They will have little if any influ-
ence on propagation of pressure transients at some times while they may
be responsible for producing important secondary pressure surge events
at another stage of the hydraulic transient.
Additional boundaries are also required to represent pressure tran-
sient suppression equipment. Some of the equations used to model
response of such equipment are discussed when considering specific
forms of protection in later chapters.
A further type of boundary condition is that which is introduced
by the modeller for convenience to simplify or reduce the work of
analysis. This form of boundary is purely a numerical device and need
not correspond with any physical feature of the pipeline network.
A common assumption with most models is that at any instant
of time, flow behaviour at the boundary is identical to that which
would occur under steady flow. For example, the head drop through
a valve or other fitting at some transient flow rate Q ¼ QðtÞ would
be taken as identical to the head loss if Q were a constant flow
rate.
6.2 Reservoirs and tanks
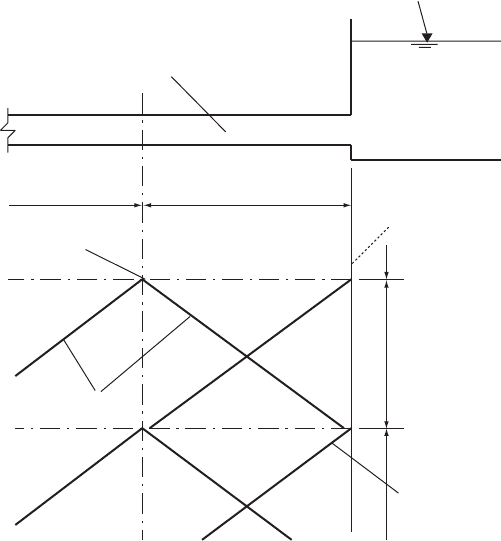
Piezometric level H
r
at a pipe inlet may be taken as constant and equal
to the free-surface water level as in the case of a large reservoir, or as
relatively slowly varying with time or possibly changing periodically
with surface wave action.
When flow is from the pipeline into the reservoir piezometric level
just inside the pipe, H will effectively be the same as in the reservoir,
thus H ¼ H
r
.
Taking that characteristic arriving at the pipe inlet for time t
(Fig. 6.2), then the quasi-invariant relationship gives:
V g=aH ¼ J or V ¼ J ðÞg=aH
r
62
Pressure transients in water engineering
When flow is into the pipeline from the reservoir, kinetic energy is
developed and losses are incurred so that H
r
¼ H þð1 þ K
L
ÞV
2
=ð2gÞ,
where K
L
is the entry loss coefficient. The relationships at the pipe
inlet at any time t become:
V g=aH ¼ J and H ¼ H
r
ð1 þ K
L
ÞV
2
=ð2gÞ
Substituting for H then:
ð1 þ K
L
Þ=ð2gÞV
2
ðÞa=gV þ a=gJH
r
¼ 0 ð6:1Þ
This quadratic equation can be readily solved for V and, by substituting in
the quasi-invariant relationship, H can be determined. For further details
of the solution see section 6.5 below. In many instances of waterworks
practice, velocity is relatively low so that ð 1 þ K
L
ÞV
2
=ð2gÞ is small. For
instance if V ¼ 1 m/s and K
L
¼ 0:5, ð1 þ K
L
ÞV
2
=ð2gÞ¼7:6cm. At
relatively low velocities it is quite acceptable to set H ¼ H
r
for both
63
Internal node
Dt
Single characteristic
arrives at boundary
Boundary node
Pipeline
Reservoir level = H
r
Characteristics
Dx
Fig. 6.2. ‘Large’ reservoir boundary
Boundaries
inflow and outflow. Then the solution for velocity V is simply:
V ¼ J ðÞg=aH
r
ð6:2Þ
In other circumstances, for instance in hydropower applications or
when studying transients in the outflow pipelines of high dams, the
velocities can be greater by an order of magnitude or more. If velocity
is 30 m/s — not unusual for dam outlet works — V
2
=ð2gÞ¼45:9m,
which clearly cannot be neglected and the quadratic form of equation
(6.1) is necessary.
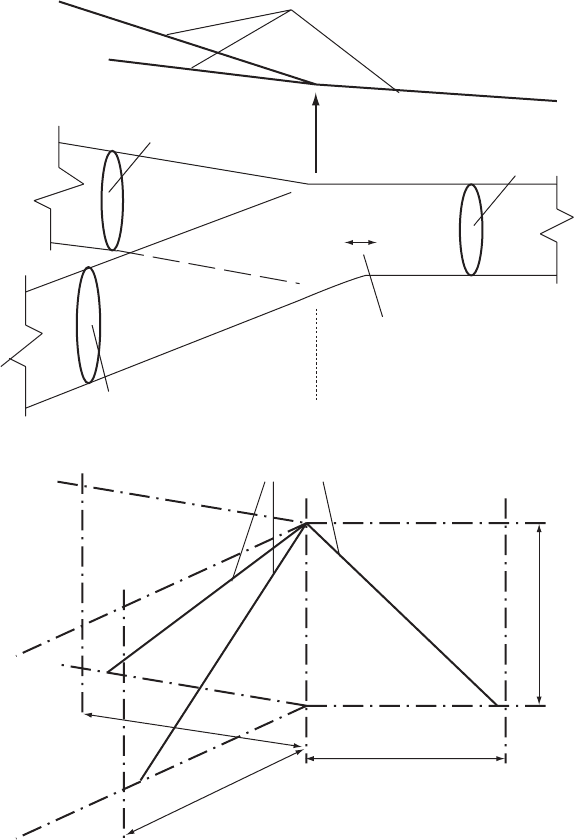
6.3 Branches and changes in pipe properties
Branches are a common feature of many pipeline networks. Consider a
simple connection of three pipes as illustrated in Fig. 6.3a.
Each of the three pipes has a boundary at the junction of the set of
pipelines. The x—t planes for each pipe can be shown as meeting
along a common time axis as depicted in Fig. 6.3b. In general the
positive direction of flow in any pipe may be directed either towards
the junction or away from the junction. Accordingly the Riemann
quasi-invarient travelling along a characteristic towards the junction
may be either of the Jþ or the J type depending upon the assigned
þve direction of flow in that pipe.
From the infinity of characteristics approaching the junction along
any pipe i, that path is chosen which arrives on the common time
axis at the instant t when a solution is to be found. The characteristic
for pipe i will provide a quasi-invarient value J
i
at time t on the common
time axis. An equation of the form:
V
i
g=a
i
H ¼ J
i
is thus obtained for each characteristic at the junction. A common
piezometric head H has been assumed at the junction end of each
pipe — that is, the velocity head in each pipe is considered to be
negligible. In water supply, economic velocities are normally of the
order of 1 m/s while sewage rising mains will usually carry flows at
higher velocities, say up to 3 m/s or more, often to ensure self-cleansing.
Velocity head will thus be of the order of 0.05—0.5 m. Ignoring the
change in velocity head from one pipe to another in these conditions
will in general not lead to significant error. Other applications may
require more careful consideration of velocity changes; for example, in
the pressure pipelines or penstocks of a hydroelectric plant, the flow
velocity can be much higher with velocities through relief valves as
64
Pressure transients in water engineering
high as 60 m/s. Velocity at the emergency closing valves of a dam can be as
high as 30 m/s. Velocity head V
2
=ð2gÞ then becomes much more substan-
tial in these circumstances. Supposing a pipe junction is made between
pipes having cross-sectional areas A
1
¼ 1m
2
and A
2
¼ 2m
2
(Fig. 6.4).
At a flow rate of 20 m
3
/s the change in piezometric level between the
65
Piezometric lines for pipes 1, 2 and 3
Common head = H measured
from horizontal datum
Positive direction of flow may be
defined as towards the junction or
away from the junction in any pipe
Pipe No. 2
Pipe No. 1
Pipe No. 3
Area = A
2
Area = A
1
Area = A
3
(a)
1
Dx
3
Dx
2
Dx
1
C
1
C
3
C
2
D
t
(
b
)
Characteristics arriving at the junction
Fig. 6.3. Representation of a pipe junction
Boundaries
pipes, ignoring losses, is 15.3 m — a quantity which cannot be ignored.
Consideration of energy losses and of kinetic energy changes becomes
necessary and calculation of piezometric level changes based on the
assumption of common head at the junction is no longer acceptable.
Returning to the simpler case where it is acceptable to neglect
velocity head changes at the junction then ignoring compressibility of
the relatively small volume of water at the junction, conservation of
volume yields:
X
ðA
i
V
i
Þ¼0 ð6:3Þ
where the summation is over all contributing pipes. Substituting for V
i
then:
V
i
¼ J
i
ðÞg=a
i
H
66
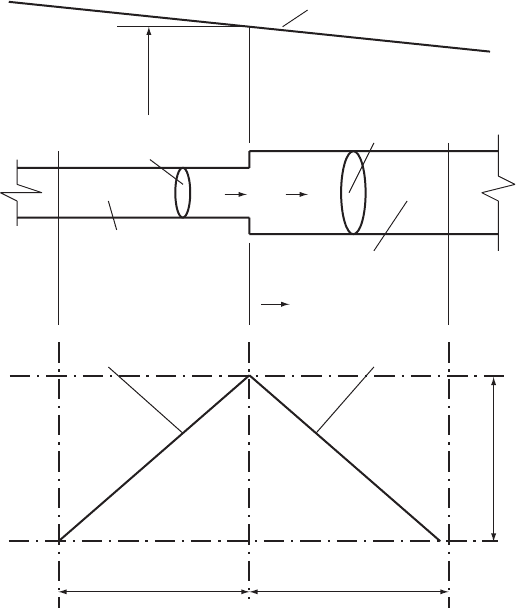
+
x
V
1
V
2
Dx
2
Dt
Dx
1
Piezometric line or hydraulic gradient
C+ characteristic C– characteristic
Wave speed = a
1
Wave speed = a
2
Area = A
1
Area = A
2
Common head = H
Fig. 6.4. Closed-end or blank flange boundary
Pressure transients in water engineering
and in the conservation equation:
X
½A
i
ðJ
i
ðÞg=a
i
HÞ ¼ 0
or
X
ðA
i
J
i
Þ¼g
X
ðA
i
=a
i
ÞH
giving,
H ¼ 1=g
X
ðA
i
J
i
Þ=
X
ðA
i
=a
i
Þð6:4Þ
If the assigned positive direction of flow in pipe i is towards the junction
then the plus sign is used for that pipe otherwise the minus sign is used.
Through induction, equation (6.4) can be shown to apply to any
number of pipes m, where 1 m 1, meeting at a junction. This
equation (6.4) for the junction of m pipes is the simplest form obtain-
able and this equation can be enhanced to include the presence of
air or gas at the junction, or isolating valves on each branch, which
may be either open or shut.
The corresponding velocity at the junction end of any pipe i at
time t is given by substituting the value of H obtained above, into
the equation for the quasi-invarient value J
i
at the junction end of
the pipe. Thus:
V
i
¼ J
i
ðÞg=a
i
H ð6:5Þ
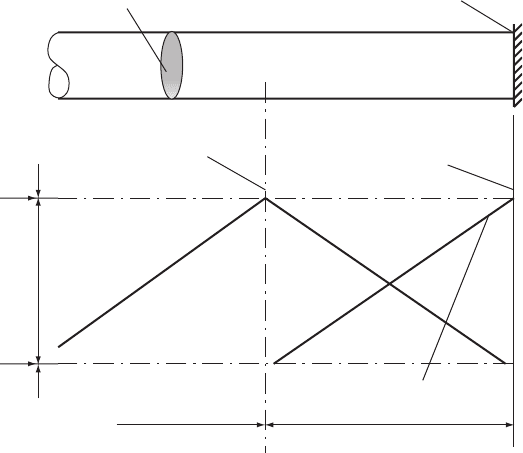
6.3.1 Specific cases — number of pipes ¼1
When the number of pipes ¼1 the equation represents the solution at a
closed end or blank flange (Fig. 6.5). Thus:
H
1
¼ 1=gðÞA
1
J
1
=ðA
1
=a
1
Þ or H
1
¼ a
1
=gJ
1
ð6:6Þ
and
V
1
¼ J
1
g=a
1
H
1
or V
1
¼ J
1
g=a
1
a
1
=gJ
1
or V
1
¼ 0 ð6:7Þ
6.3.2 Specific cases — change of cross-sectional area
When the number of pipes ¼2 the equation can be used to represent
some change of pipe properties, either a change of cross-section,
material, wall thickness or resistance. With reference to Fig. 6.5, then
ignoring changes of kinetic energy and losses at the junction of pipes:
H ¼ 1=gðþA
1
J
1
A
2
J
2
Þ=ðA
1
=a
1
þ A
2
=a
2
Þð6:8Þ
67
Boundaries
Velocities in pipes 1 and 2 are respectively given by:
V
1
¼ J
1
g=a
1
H and V
2
¼ J
2
þ g=a
2
H ð6:9Þ
Any change of pipe material, wall thickness or diameter will lead to a
change of wave speed a. Wave speed may also be altered by the
pressure-dependent gas concentration in a pipe.
A special case of a change in cross-sectional property is where a pipe-
line terminates at a reservoir (Fig. 6.2). Suppose the þve direction of
flow is into the reservoir. Within the reservoir V
2
¼ 0 ¼ constant
and H
2
¼ H
r
ðtÞ where H
r
ðtÞ is a slowly varying function of time or
may be constant. The reservoir cross-section A
2
is very large com-
pared to pipe area A
1
and wave speed in the reservoir can be taken
as the speed in an unconfined body of water — that is, a
2
¼
p
ðK=Þ,
then:
J
2
¼ V
2
g=a
2
H
2
¼g=a
2
H
r
H ¼ 1=gðþA
1
J
1
A
2
J
2
Þ=ðA
1
=a
1
þ A
2
=a
2
Þ
H ¼ 1=gðþA
1
J
1
A
2
g=a
2
H
r
Þ=ðA
1
=a
1
þ A
2
=a
2
Þ
68
Dt
Single characteristic
at boundary
Dx
Blank flange or closed endPipeline
Boundary node
Internal node
Fig. 6.5. A change of cross-section
Pressure transients in water engineering
since
A
1
=a
1
A
2
=a
2
and jA
1
C
1
jjA
2
g=a
2
H
r
j
H ¼ 1=gðA
2
g=a
2
H
r
Þ=ðA
2
=a
2
Þ
or
H ¼ H
r
6.4 Response of a large pipe or trunk main
It is not uncommon for work to be carried out on parts of an extensive
network of interconnected pipelines. Pressure transients are no
respecters of contract boundaries and will spread throughout a system
of pressure pipes until a shut valve/closed end or a reservoir is
encountered. From each of these the pressure wave may be taken as
reflected 100% in one form or another. If the entire network were to
be modelled then the workload could be very considerable, not least
in the effort required to obtain adequate information on other parts
of a large system outwith the contract area of immediate interest. It
may be acceptable, in certain circumstances, to limit the extent of
modelling by an approximation at some important point of wave reflec-
tion within the system as a whole.
Suppose, for example, a large pipeline, trunk main or aqueduct supplies
a number of smaller branch networks as illustrated in Fig. 6.6. Suppose
work is to be carried out on one of these branched systems including a
hydraulic transient investigation. Pressure transients created within the
branched system will propagate upstream towards the connection of
the branch with the main aqueduct. Assume an initial steady velocity
V
o
exists in the branch main just downstream of the connection. If the
initial steady-state piezometric level at the junction is H
o
then setting
the datum for head measurements at this level H
o
¼ 0. Should the
initial velocity be reduced to zero by valve closure in the branch
network then the inertial head rise H
b
in the branch main will be:
H
b
¼ aV
o
=g ð6:10Þ
Ignoring changes due to resistance and pipe elevation variation, then
the invariant value J leaving the shut valve just after its closure, is
given by:
J¼V g=aH ¼ 0 g=aða=gV
o
Þ¼V
o
ð6:11Þ
In the upstream section of the aqueduct, assuming all flow entering
the branch comes from this direction and that no other flows are
69
Boundaries
present:
Jþ¼V
o
A
b
=A
a
þ g=a0 ¼ V
o
A
b
=A
a
ð6:12Þ
And from the downstream section of aqueduct where zero flow is taking
place:
J¼0 þ g=a0 ¼ 0 ð6:13Þ
Due to valve closure in the branch main, the head change H
j
at the
junction of the branch main with the aqueduct is given by equation
(6.4). Substituting in this equation then:
H
j
¼ 1=g½ðV
o
ÞA
b
þ V
o
A
b
=A
a
A
a
0A
a
=ðA
b
=a
b
þ A
a
=a
a
þ A
a
=a
a
Þ
or
H
j
¼ 2=gA
b
V
o
=ðA
b
=a
b
þ 2A
a
=a
a
Þð6:14Þ
Head rise at the junction as a proportion of the initial head rise at the
valve in the branch is then:
H
j
=H
b
¼ 2=½1 þ 2ðA
a
=a
a
Þ=ðA
b
=a
b
Þ
70
+x
+x
J+ = V
o
A
b
/A
a
J– = –V
o
J– = 0
A
a
A
b
+x
Fig. 6.6. Small branches connected to trunk main
Pressure transients in water engineering
or for
a ¼ constant H
j
=H
b
¼ 2=ð1 þ 2A
a
=A
b
Þ
Inserting values for area and wave speed into the above equation it
can be shown that as aqueduct area/branch area increases the response
at the connection tends more and more towards that of a simple reser-
voir. This relationship allows the investigator to assess the implication
of replacing the aqueduct connection by a simpler boundary such as a
reservoir.
6.5 Actuated valves and pipeline fittings
In the case where isolating valves such as gate valves or butterfly valves
are distributed along a pipeline at intervals to facilitate maintenance
and these valves remain open throughout a transient event, the head
drop through each valve is relatively small and so there is little to be
gained by modelling each valve as an internal boundary. It is usually
sufficient to establish the overall head loss coefficient for all of the
valves and to distribute this along the pipeline together with other
minor losses from bends, tees, etc., to yield an overall resistance
coefficient. Overall head loss H
f
is given by:
H
f
¼
X
ðK
L
ÞþfL=D
no
V
2
=ð2gÞ¼f
e
L=DV
2
=ð2gÞð6:15Þ
where f
e
¼ f þ
P
K
L
D=L.
Other valves or fittings may impose significant head losses on the
flow even when fully opened and so warrant inclusion in a model as a
discrete head loss. Where a valve may operate to open or close
during a transient event it is essential to include this as a discrete
head drop in the model.
In general a manufacturer will provide data on the relationship
between flow rate and head loss through a valve in the form of a
head loss coefficient curve as a function of valve position. The head
loss coefficient K
L
is documented as a function of valve stroke between
the fully open position and some point near to the shut position.
Figure 6.7 depicts typical head loss coefficients for a range of valve
types. Due to the very non-linear relationship between K
L
and stroke,
particularly as a valve nears the closed position, it is not advisable to
interpolate values of K
L
directly. Rather the head loss relationship
should be represented in a way that endeavours to reduce the degree
of non-linearity. A simple approach is to interpolate values of 1=
p
K
L
.
71
Boundaries
