Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour
Подождите немного. Документ загружается.


72
Valve position as a proportion of port stroke, n
(a)
K
o
n
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
10
1
A
B
F
C
E
Valve type* D (in.) a
o
/A Port shape
A Gate 12 1.0 Circular
B Butterfly 24 0.65 –
C Globe 6 1.0 Shaped (iii)
D
1
'In-line' regulator 12 1.0 Rectangular
D
2
'In-line' regulator 9 Shaped (i)
G
D
1
D
2
1000
100
10
1
0.1
0.1
Valve headloss coefficient, K
n
n
n
n
iiiii
Port shapes
* See Fig. 4
† Model
i
Valve full open
Valve type* D (in.) a
o
/A Port shape
E Submerged disch.
regulator 6 1.0 Rectangular
F Sleeve regulator 12 1.0 Shaped (ii)
G Free disch. regulator 8* 2.0 Rectangular
D In-line regulator G Free discharge regulato
r
E Submerged discharge regulator
(b)
F Sleeve regulator
Fig. 6.7. (a) Head-loss coefficients for different valve types; (b) control valve type
Pressure transients in water engineering
6.5.1 Terminal valves
Consider a valve located at the extremity of a pipeline as shown in
Fig. 6.8. At any instant of time a characteristic will arrive at the
valve from the pipeline providing the quasi-invariant relationship
between H and V at the valve:
V g=aH ¼ J
A second relationship is provided by the head loss equation for the
valve:
H ¼ S
j
S
v
K
L
V
2
=ð2gÞð6:16Þ
where H ¼ H H
r
, S
j
¼þ1 for a Cþ characteristic and S
j
¼1 for
a C characteristic; also S
v
¼ V
o
=jV
o
j. Substituting for H
r
then:
S
j
½S
j
S
v
K
L
=ð2gÞV
2
þ H
r
g=a þ V J¼0
or rearranging,
S
v
K
L
=ð2aÞV
2
þ V þ S
j
g=aH
r
J¼0
Solving for V then:
V ¼ S
v
a=K
L
½
p
f1 þ 2S
v
K
L
=aðJS
j
g=aH
r
Þg 1ð6:17Þ
73
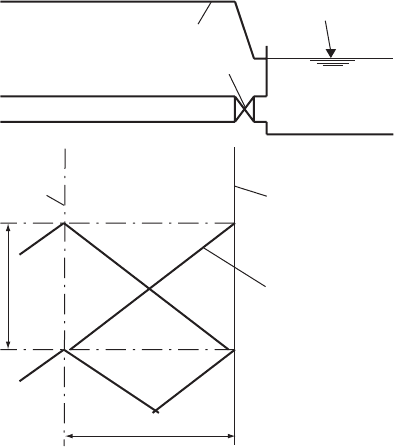
Boundary
Single characteristi
c
at boundary
Discharge level = H
r
Piezometric level = H
Pipeline Valve
Internal node
Dx
Dt
Fig. 6.8. Valve at a reservoir or tank
Boundaries
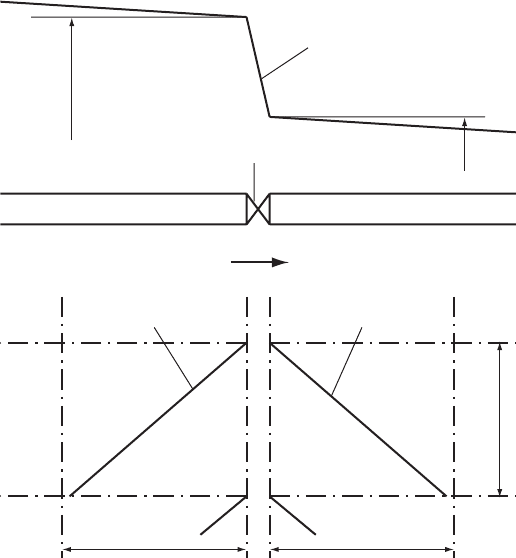
6.5.2 In-line valve
Upstream and downstream of the valve are stretches of pipeline within
which pressure transients can propagate (Fig. 6.9).
From the upstream and downstream pipelines characteristics will
arrive at the valve at any time t. The invariant relationships are:
V
u=s
þ g=a
1
H
u=s
¼ Jþ for the Cþ characteristic
and V
d=s
g=a
2
H
d=s
¼ J for the C path
Across the valve:
H
d=s
H
u=s
¼ S
j
S
v
K
L
=ð2gÞV
2
and from conservation of volume:
V
u=s
A
u=s
¼ VA ¼ V
d=s
A
d=s
74
Dx
D
t
Dx
H
u/s
H
d/s
C+ characteristic C– characteristic
Valve
Piezometric line
+
Fig. 6.9. In-line valve
Pressure transients in water engineering
Eliminating H
u=s
, H
d=s
, V
u=s
and V
d=s
then writing:
constant ¼ S
v
A=K
L
ða
u=s
=A
u=s
þ a
d=s
=A
d=s
Þ
V ¼ constantð1
p
f1 2S
v
=K
L
constantða
u=s
Jþþa
d=s
JÞg
ð6:18Þ
For both the terminal valve and the in-line valve additional measures
have to be taken to accommodate the gaseous void fraction and possible
vapour cavity formation.
6.5.3 Automatic control valves
Valves may be installed for the purpose of regulating pressure and/or
flow within part of a network. Various alternatives are possible and
some of these are considered.
6.5.3.1 Pressure-reducing valve
This valve is set to reduce a constant or variable inlet pressure and to
provide a constant outlet pressure. The valve is adjusted to produce a
constant outlet pressure head H
c
or piezometric level so that with
reference to Fig. 6.9, H
d=s
¼ H
c
. Then the C characteristic yields
an invariant value,
J¼V g=aH
c
or V ¼ Jþg=aH
c
Then on the inlet side of the valve the Cþ characteristic gives,
Jþ¼V þ g=aH
u=s
or substituting the value of velocity,
H
u=s
¼ a=gðJþVÞð6:19Þ
When the valve is fully opened,
H
d=s
¼ H
u=s
K
o
V
2
=ð2gÞð6:20Þ
where K
o
is the valve head loss coefficient when fully opened. If
H
d=s
< H
c
, control cannot be maintained and a solution for the fully
opened valve is used.
6.5.3.2 Pressure-sustaining valve
This valve is set to maintain a constant inlet or upstream pressure so
that H
u=s
¼ H
c
. The Cþ characteristic yields a quasi-invariant value
75
Boundaries
Jþ at the valve inlet so that,
Jþ¼V þ g=aH
c
or velocity V ¼ Jþg=aH
c
Then on the outlet side of the valve,
J¼V g=aH
d=s
or H
d=s
¼ a=gðJVÞð6:21Þ
When the valve is fully opened,
H
u=s
¼ H
d=s
þ K
o
V
2
=ð2gÞð6:22Þ
If H
u=s
> H
c
then the downstream head is too high to allow the set head
to be maintained. If the valve is shut then V ¼ 0:0 and at the valve
inlet,
Jþ¼0 þ g=aH
u=s
or H
u=s
¼ a=gJþ
If H
u=s
< H
c
then the downstream head is too low to allow the set inlet
head to be maintained.
6.5.3.3 Demand-sensing pressure-reducing valve
In this configuration a minimum or base outlet pressure or deliver head
H
b
is set. This head will apply at zero flow. The valve is adjusted to
produce a delivery head variation of the form,
H
d=s
¼ H
b
þ K
L
V
2
=ð2gÞ
where K
L
is a coefficient defining the relationship between velocity and
head. Then on the delivery side of the valve,
J¼V g=aH
d=s
¼ V g=a½H
b
þ K
L
V
2
=ð2gÞ
Rearranging,
K
L
=ð2aÞV
2
V þ g=aH
b
J¼0
or
V ¼ a=K
L
f1
p
½1 2K
L
=aðg=aH
b
JÞg ð6:23Þ
then
H
d=s
¼ H
b
þ K
L
V
2
=ð2gÞ
On the inlet side of the valve,
Jþ¼V þ g=aH
u=s
or H
u=s
¼ a=gðJþVÞ
76
Pressure transients in water engineering
For a viable result H
u=s
H
d=s
K
o
V
2
=ð2gÞ where K
o
is the fully open
valve head loss coefficient.
6.6 Use of more than one time step
If the modelling exercise is only one part of an overall study of hydraulic
transients in a system then the computer model may reasonably be
expected to encompass the entire network. As pipe lengths within a
pumping station, for example, may be quite short, this implies a small
time increment which may not be particularly suitable for the much
larger pipe lengths of the majority of the network. A modified com-
putational scheme which was described by Vardy (1976) may be
useful in this context. The current author has used this technique on
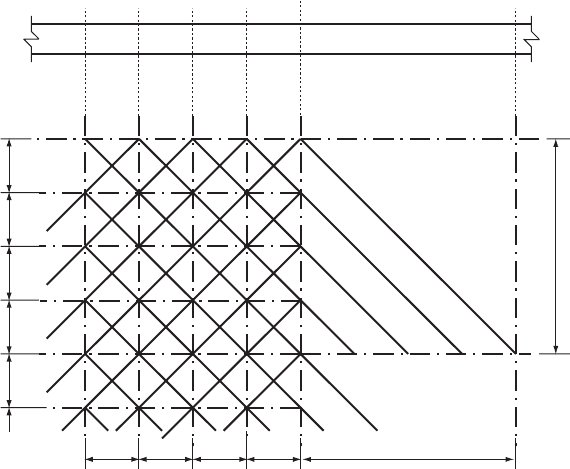
a number of occasions in these circumstances. Consider Fig. 6.10.
Two distinct time steps are in use. A small time increment is
employed within the vicinity of the pumping station so that
x
p
=t
p
jV aj for the small lengths of pipe x. Outwith the
77
Pipeline
DxDx
p
Dt
p
Dt
p
D
t
Dt
p
Dt
p
Dt
p
Dx
p
Dx
p
Dx
p
Fig. 6.10. Inclusion of a change in time step
Boundaries
pumping station, larger x increments can be used with correspond-
ingly increased t.
Computations in the pumping station are carried out using the fine
grid spacing x
p
and the corresponding small time step t
p
, while in
the system as a whole a larger increment size x and time increment
t are used. The relationship between the time increments is:
t ¼ m t
p
where m is a positive integer.
The ‘boundary’ between use of large and small increment sizes is
placed at a location such that any significant factors which could
have an influence on transient behaviour in the pumping station are
included in the fine grid part of the system. These factors might
include pressure vessels and air valves for example. If a booster
pumping station with significant lengths of suction main is being
modelled, a second upstream ‘boundary’ or interface is required
between the main grid spacing and the fine grid spacing.
Transients developed within the pumping station are modelled in
greater detail than are events in the overall system. Once a pressure
wave has passed through the interface into the system as a whole,
detail will be lost where wave components have a short period <t.
This will not materially influence predictions of events within the
detailed area at least for some time until wave reflections from
outwith the fine grid area return to the ‘boundary’.
6.7 Non-reflecting boundary
If interest is centred on transient behaviour initiated within the detailed
area alone and transient behaviour in the system as a whole does not
require to be modelled then it may be possible to terminate the computer
model at a section local to the area of interest, say a pumping station.
This can be done when it is considered that the transient event of
interest occurs in a time t the wave reflection time from the nearest
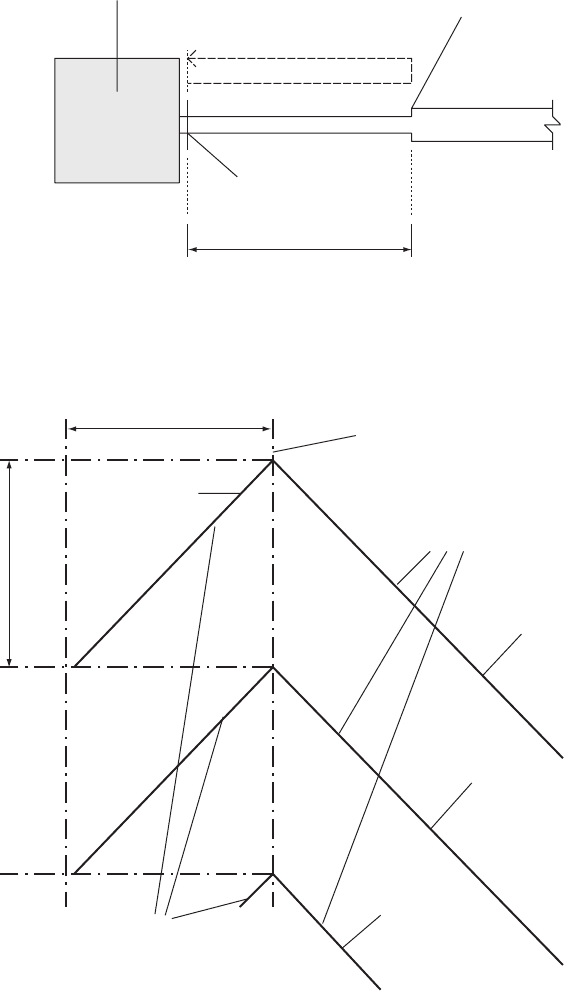
feature which will produce a significant response (Fig. 6.11) — that is,
time of modelling t 2L=a. In this instance a non-reflecting boundary
can be introduced close to the pumping station. Suppose we have a
boundary to which no pressure wave effects arrive from one side and
the Riemann invariant remains at steady-state values, for example
steady design flow rate. Figure 6.12 illustrates this circumstance.
Let the initial conditions at a non-reflecting boundary be represented
by velocity V
o
and piezometric level H
o
. Then the invariant value is
78
Pressure transients in water engineering
79
L
First point of significant reflection
Part of pipeline to be modelled
Non-reflecting boundary
Reflection time = 2L/a
Fig. 6.11. Simple non-reflecting boundary
J
o
=
V
o
±
g
/
aH
o
J
o
=
V
o
±
g
/
aH
o
J
p
=
V
p
±
g
/
aH
p
J
o
=
V
o
±
g
/
aH
o
Characteristics without
the area being modelled
Initial conditions
V
o
and
H
o
Characteristics within the
area being modelled
Non-reflecting boundary
Dt
Dx
Fig. 6.12. Characteristics at a non-reflecting boundary
Boundaries
given by:
J
o
¼ V
o
g=aH
o
ð6:24Þ
If no reflection or transient effects arrive at the boundary from the main
network then the value J
o
will remain the same regardless of the time
which has elapsed. From within the modelling area the pressure wave
effect from the transient event will be given by the prevailing values
of velocity V
p
and H
p
as shown in Fig. 6.12. So that:
J
p
¼ V
p
ðÞg=aH
p
ð6:25Þ
is the quasi-invariant value at the end of the segment of characteristic
leading to the point t at which a solution is to be found. The effects of
friction and any other influences along the segment of path have been
added to yield this final value of J
p
. The solution after any time step is
then given by:
V ¼ðJ
p
þ J
o
Þ=2 and H ¼ðJ
p
J
o
Þ=ð2g=aÞð6:26Þ
This technique is clearly approximate since although no effects will
return to the boundary from features along the pipeline such as
changes of cross-section, bifurcations, valves, etc. there will be a
more gradual and continuous change due to the action of pipeline
resistance. If necessary, some allowance can be made for this effect by
slowly modifying the value of J
o
over time, producing a quasi non-
reflecting boundary. A modified technique which includes the effect
of resistance in the system outwith the modelled area can be found in
Chapter 20.
Non-reflecting boundaries can be used in a variety of contexts. Two
such boundaries can be employed on either side of a booster pumping
station for instance, as depicted in Fig. 6.13. The non-reflecting
boundary can be used in many circumstances. For instance, consider
the case of branch pipe network connected to a larger aqueduct
system. If only events within the branch network are of interest then
non-reflecting boundaries could be installed a short distance along
the aqueduct on each side of the connection point. Alternatively, the
junction itself could be made non-reflecting using the same principle,
by introducing the initial steady flow values of velocity and head in
the aqueduct upstream and downstream of the junction, so that head
at the junction H
j
becomes:
H
j
¼ðJ
b
A
b
þðV
o
A
b
=A
a
þ g=a
a
H
o
ÞA
a
ð0A
b
=A
a
g=a
a
H
o
ÞA
a
Þ=ð2A
a
=a
a
þ A
b
=a
b
Þ
80
Pressure transients in water engineering
or
H
j
¼ðV
o
A
b
þ 2g=a
a
H
o
A
a
J
b
A
b
Þ=ð2A
a
=a
a
þ A
b
=a
b
Þ
¼ðconstant J
b
A
b
Þ=ð2A
a
=a
a
þ A
b
=a
b
Þð6:27Þ
where constant ¼ V
o
A
b
þ 2g=a
a
H
o
A
a
.
There are limitations to the application of the above approach.
Clearly the period of analysis has to be limited to < 2L=a where this
is the reflection time from the non-reflecting boundary to the first
source of significant reflection in the pipeline system outwith the area
of interest. The use of this type of boundary is also approximate in
the sense that reflections are continually being transmitted back from
81
J
+o
=
V
u
/
s
(o)
–
g
/
aH
u/s(o)
J
–o
=
V
d/s(o)
–
g
/
aH
d/s(o)
u/s piezometric line
d/s piezometric line
H
d/s
H
u/s
Non-reflecting boundary Non-reflecting boundary
Booster
pumping
station
Normal schematisation
between non-reflectin
g
boundaries
Dt
Dx
Dx
C– characteristics from u/s
pipeline with invariant value
J
+o
C– characteristics from d/s
pipeline with invariant value
J
–
o
Fig. 6.13. Non-reflecting boundaries at a pumping station
Boundaries
