Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour

Подождите немного. Документ загружается.

and subtracting equation (2.7) from equation (2.5) then:

@V=@t þðV  aÞ@V=@x  g=að@H=@t þðV  aÞ@H=@x þ gS

þ g=aV dz=dx ¼ 0

The derivatives @ðÞ=@t þðV  a Þ@ðÞ=@x represent total rates of

change in the variables V and H along paths dx=dt ¼ V  a in the

x—t plane and the equations can be written as ordinary differential

equations along these paths so that:

dV=dt þ g=a dH=dt þ gS  g=aV dz=dx ¼ 0 ð4:1Þ

along dx=dt ¼ V þ a ð4:2Þ

and

dV=dt  g=a dH=dt þ gS þ g=aV dz=dx ¼ 0 ð4:3Þ

along dx=dt ¼ V  a ð4:4Þ

Multiplying throughout these equations by dt then:

dV þ g=a dH þ gS dt  g=aV dz=dx dt ¼ 0 along dx=dt ¼ V þ a

and

dV  g=a dH þ gS dt þ g=aV dz=dx dt ¼ 0 along dx=dt ¼ V  a

Integrating the equations along the paths dx=dt ¼ V  a then:

dV þ g

1=a dH þ g

S dt  g

V=½aðV þ aÞdz ¼ constant

along dx=dt ¼ V þ a

and

dV  g

1=a dH þ g

S dt þ g

V=½aðV  aÞdz ¼ constant

along dx=dt ¼ V  a

or if a is assumed constant:

V þ g=aH ¼ constant  g

S dt þ g

V=½aðV þ aÞdz ð4:5aÞ

along dx=dt ¼ V þ a ð4:2Þ

Pressure transients in water engineering

and

V  g=aH ¼ constant  g

S dt  g

V=½aðV  aÞdz ð4:6bÞ

along dx=dt ¼ V  a ð4:4Þ

Neglecting the terms g

S dt and g

V=½aðV  aÞdz for the moment

gives the simple linear equations:

V þ g=aH ¼ constant ð4:5bÞ

along dx=dt ¼ V þ a

and

V  g=aH ¼ constant ð4:6bÞ

along dx=dt ¼ V  a

The paths dx=dt ¼ V  a are ‘characteristics’ of the system. The

derivation of the ‘characteristic’ equations given above represents a

simple approach. There are more sophisticated and elegant derivations.

Characteristics are features of many engineering disciplines and for an

introduction to the application of the ‘Method of Characteristics’ the

book by Abbott (1966) is highly recommended.

The constant or ‘invariant’ quantity in each of the above equations

(4.5b) and (4.6b) is often named after Riemann, who was one of the

ﬁrst to use what has become known as the ‘Method of Characteristics’.

He applied this method to the ﬁeld of gas dynamics in the mid-19th

century. Abbott used the symbol J to denote this invariant quantity

so that, neglecting the integrals on the right-hand side of the equations:

V þ g=aH ¼ Jþ along dx=dt ¼ V þ a

and

V  g=aH ¼ J along dx=dt ¼ V  a

As written above, the invariant J has units of velocity. Alternatively,

the invariants could be in units of head by multiplying throughout by

a=g, giving:

H  a=gV ¼ J

In this book J has been used in terms of velocity. There are no compel-

ling reasons for this choice other than that being in units of velocity the

quantities involved are typically small with possibly smaller risk of

misplacing the decimal point when carrying out manual calculations.

Characteristic equations

Also in other applications of characteristics such as to free surface ﬂow

transients or to supercritical steady ﬂow, equations are in terms of velo-

city without the option to convert to other units. It could also be

mentioned that in the presence of free air or gas a becomes a function

of H and so having the term g=aH seems appropriate.

4.2 Signiﬁcance of the integrals

The pair of integrals on the right-hand side of the equations represent the

effects of pipeline ﬂow resistance g

S dt and changes in pipeline ele va-

tion g

V=½aðV  aÞdz. These terms still exist even under steady

ﬂow. Including these effects renders the quantity J quasi-invariant with

the value changing gradually along the paths dx=dt ¼ V  a.

The following sections consider each of these integrals in isolation.

4.3 Effect of changing pipe elevation

Neglecting pipeline resistance for the moment, along a path

dx=dt ¼ V  a the equations for the quasi-invariants become:

V  g=aH ¼ Jg

V=½aðV  aÞdz ð4:5cÞ

Ignoring any small changes in kinetic energy head then in the absence

of pipeline resistance and losses generally H remains essentially

constant along a path dx=dt ¼ V  a so that along some length of

conduit over which velocity changes by an amount dV and over

which pipeline elevation changes by an amount dz:

dV ¼g

V=½aðV  aÞdz or since V  a; dV  g

V=a

Considering steady motion, mass ﬂow is constant, or: AV ¼ constant,

therefore,

ð þ dÞðA þdAÞðV þ dVÞ¼AV

Neglecting second-order effects and dividing throughout by mass ﬂow

rate:

d= þ dA=A þ dV=V ¼ 0

then,

1=  d=dp þ 1=A  dA=dp ¼1=V  dV=dp

Pressure transients in water engineering

and substituting:

1=K þ Dc

=ðsEÞ¼1=V  dV=dp

Since pressure change dp is due entirely to elevation change dz then

dp ¼g dz, or,

½1=K þ Dc

=ðsEÞ ¼ 1=V  dV=ðg dzÞ

Substituting a

and rearranging,

gV=a

dz ¼ dV

Between limits 0 and 1 then:

 V

¼ g

V=a

dz ð4:7Þ

The equation can also be integrated in steady ﬂow to give,

g=a

dz ¼ dV=V or; g =a

ðz

 z

Þ¼lnðV

where symbol lnðÞdenotes the natural logarithm, so that ﬁnally,

¼ V

exp½g=a

ðz

 z

Þ ð4:8Þ

The above demonstrates that this small integral represents the

velocity difference caused by compression or expansion of the liquid

and changes in pipe cross-section due to pressure change arising from

variations in pipeline elevation and, where resistance is included,

changes of piezometric level. This effect exists in steady ﬂow as well

as under transient conditions and most investigators would normally

ignore this term although its signiﬁcance is more important when hand-

ling modern plastic materials which are more prone to deformation.

4.4 Pipeline resistance

The pipeline resistance term g

S dt requires use of a resistance law

derived from steady ﬂow measurements and it is assumed that this is

applicable under transient ﬂow circumstances. For determining resistance

in a pipeline or tunnel system it is best to have on-site measurements but

this is not feasible in many instances, especially if it is a new scheme yet to

be constructed. Selection of an appropriate coefﬁcient or coefﬁcients

should err on the side of caution. In steady ﬂow concerning say a

pumping main, typically for pump selection a roughness coefﬁcient

would be chosen towards the upper limit of the range of likely values.

This ensures that the pump selected is able to develop the necessary

Characteristic equations

head. However, in transient studies where velocity changes are con-

cerned, pressure transients may be more severe if velocity is greater,

implying that roughness should be selected at the lower end of the scale

of likely values. Generally it is wise to study surging using alternative

roughness values to ensure that worst-case conditions have been

included.

Early experiments around 1850 on ﬂow of water indicated that head

loss hf varied approximately directly with velocity head V

=ð2gÞ and

pipe length L and inversely with pipe diameter D. Using a coefﬁcient

of proportionality f, called the friction factor, Darcy, Weisbach and

others proposed an equation having the form:

hf ¼ fL=DV

=ð2gÞð4:9Þ

This equation is commonly called the Darcy equation.

The value f was found generally to be dependant upon the relative

roughness k=D and on the Reynolds number Re ¼ VD= where  is

the kinematic viscosity of the liquid ¼dynamic viscosity/density.

Reynold’s experiments showed that viscosity caused two distinct ﬂow

regimes to occur. At values of Re < 2100 ﬂow was always laminar

while for Re > 4000 ﬂow was always turbulent. For laminar ﬂow all

turbulence will be damped by viscosity and no mixing will occur, while

for turbulent ﬂow a chaotic motion of small ﬂuid masses occurs in all

directions as ﬂow takes place.

Under laminar motion the friction factor is given by:

f ¼ 64=Re ð4:10Þ

Probably the most accurate formula available for calculation of

pipeline friction factor f in the transition region between laminar and

fully developed turbulent ﬂow is the Colebrooke—White equation as

described by Ackers (1963). Its implicit formulation makes it incon-

venient for application, that is:

f ¼2 log

½2:51=ðRe

fÞþk=ð3:71DÞ ð4:11Þ

where k is the equivalent uniform sand grain roughness height and

log

represents the common logarithmic function. More convenient

approximations to the Colebrooke—White equation have been devel-

oped, for example:

f ¼ 0 :25=½log

f5:74=Re

0:9

þ k=ð3:71DÞg

ð4:12Þ

Alternative equations can be used, such as the Moody formula:

f ¼ 0 :0055½1:0 þ

ð20 000:0k=D þ 10

=ReÞ ð4:13Þ

Pressure transients in water engineering

These equations allow f to be found with sufﬁcient accuracy for analysis

purposes. Values of k for different pipe materials and conditions can be

found from sources such as Miller (1978).

The value of roughness height k may vary over time within a pipe-

line and consideration must be given to this aging process. Two

principal factors should be taken into account when assessing varia-

tions in k.

4.4.1 Corrosion

Metallic pipes such as steel and cast iron are liable to corrode. Hydraulic

Research Station paper No. 4 gives some data from studies by Cole-

brooke and White (Colebrooke, 1939) whereby the increase in k may

be estimated for older asphalted cast-iron pipes. The rate of increase

in roughness height with time represented by  can be obtained from:

2 log

ð12Þ¼3:8  pH ð4:14Þ

where  ¼ ft=year for cast iron asphalted pipes. The current value of

k is then found from the equation,

k ¼ k

þ t ð4:15Þ

t being pipe age in years and k

is the new pipe roughness height.

4.4.2 Sliming

Wastewater mains are liable to sliming. Recent research has shown that

k is primarily a function of velocity:

k ¼ V

ð2:34Þ

ð4:16Þ

where

 ¼ 0:054 (lower bound)

 ¼ 0:446 (mean) and

 ¼ 3:660 (upper bound)

Ninety-ﬁve per cent of observations lie between these upper and lower

limits.

From equation (4.16) it will be noted that as V ! 0 then k ! 0. To

avoid unreasonably small values of k it is recommended that a minimum

value of k be used equal to the value k

for the clean pipe.

For all types of wastewater rising mains, the following has also been

proposed as in the Biwater Manual (1988).

Characteristic equations

For V ¼ 1:0m=s ... 0:15  k  0:6

For V ¼ 1:5m=s ... 0:06  k  0:3

For V ¼ 2:0m=s ... 0:03  k  0:15

For sludges and suspensions, the friction factor at low ﬂows, V < 1:2m/s,

may be amended from the value for clean water.

4.4.3 Evaluation of the integral

Since Reynolds number is a function of velocity, it follows that f will

require to be recalculated as an analysis progresses.

Having found f then application of the Darcy equation (4.9) allows

resistance gradient S ¼ hf=L to be established, thus:

S ¼ f=DV

=ð2gÞ

To preserve the correct sign of resistance gradient in a regime where

ﬂow may reverse then:

S ¼ f=DVjVj=ð2gÞ

When evaluating the integral g

S dt over some path length, a choice

has to be made regarding how velocity is to be represented:

S dt ¼ f=ð2DÞ

dt  f=ð2DÞV

ðt

 t

Þ or

 f=ð2=DÞðV

ðt

 t

where ðV

may be represented as

ðV

þ V

Þ; V

may be represented

ðV

þ V

Þthe arithmetic mean, or as

ðV

Þthe geometric mean,

Smith (1969).

The representation of V

ðV

Þ has some advantage as V

becomes ½

ðV

Þ

or simply V

. Preserving the sign of resistance

gradient then, this can be written V

j. In the equations for the

quasi-invariant, ignoring the second small integral for the effect of

changing pipe elevation:

V  g=aH ¼ Jf=ð2DÞVjV

jðt  t

or rearranging,

f1  ðÞf=ð2DÞjV

jðt  t

ÞgV  g=aH ¼ Jð4:17Þ

This formulation also preserves the linear nature of the equations.

Pressure transients in water engineering

Application of characteristic

equations

In the present chapter the equations derived in Chapter 4 are used in

the development of a practical method of computation of hydraulic

transient behaviour. Equations (4.2) and (4.4), obtained in the previous

chapter, describe the gradients of paths in the x—t plane along which

disturbances may propagate. In present circumstances the disturbances

are pressure waves propagating along the paths dx=dt ¼ V  a with

quasi-invariant values J.

‘Characteristics’ of a system relate to a capacity for propagation rather

than to any speciﬁc propagation event. Thus a set of characteristic

paths can be deemed to exist although there may be no transient

event taking place. In other words these propagation paths will still

be present under both steady ﬂow conditions and static conditions.

5.1 Use of the characteristics

If a wavefront is considered to be made up of an inﬁnite number of

inﬁnite wavelets or step changes in velocity and head, each of

inﬁnitesimal magnitude (Fig. 5.1), then each wavelet will travel along

a characteristic. Assume the horizontal or x-axis is used to represent

distance along a pipeline and the vertical t-axis deﬁnes time elapsed

during a transient event. An inﬁnite number of paths will exist of the

form Cþ or dx=dt ¼ V þ a within this x—t plane. Similarly there will

be an inﬁnite number of C paths with gradient dx=dt ¼ V  a

along which waves may travel in the opposite direction (Fig. 5.2).

The meeting of Cþ and C characteristics produces 1

intersection

points.

At any intersection of a pair of opposing characteristics, the invariant

relationships along these propagation paths yield two simultaneous

equations in V and H, that is:

V þ g=aH ¼ Jþ and V g=aH ¼ J

giving

V ¼ðJþþJÞ=2 ð5:1Þ

and

H ¼ðJþJÞ=ð2g=aÞð5:2Þ

Consider any typical intersection point P in this x—t plane. If a

transient event is initiated at point P, the effects will be propagated

along the Cþ and C paths which pass through the point and an

increasing length of pipeline will be affected by the event with the

passage of time. The wedge-shaped area bounded by these Cþ and

C paths is called the region of inﬂuence of P, Abbott (1966, p. 17),

and is represented by the long-dashed lines in Fig. 5.2. Flow conditions

at points outwith this area are not changed by the event at P.

Also if earlier transient conditions are travelling along the Cþ and

C characteristics which meet at P then the resulting ﬂow conditions

Horizontal datum

Piezometric line – wavefront

Wavelets

Velocity of flow = V

dx/dt = V ± a

Fig. 5.1. Representation of a pressure wave front

Pressure transients in water engineering

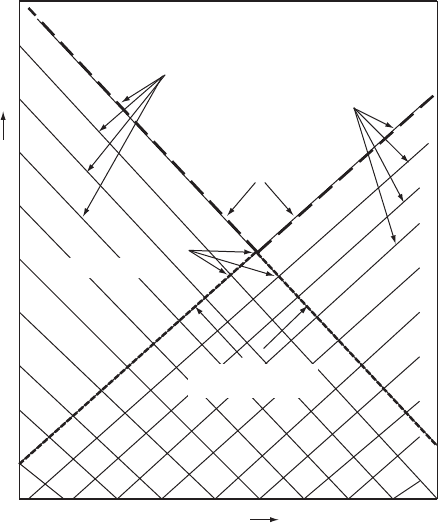
at this point will be determined only by conditions within the area

bounded by the characteristics represented by the short-dashed lines

of Fig. 5.2. This region is sometimes called the domain of dependence

of P. Points outwith this area cannot inﬂuence conditions at P.

The characteristics and their quasi-invariant relationships can be

used to provide a solution to the task of predicting propagation of pres-

sure waves. For practical purposes a representative set of characteristics,

deﬁned by the heavier lines in Fig. 5.3, is chosen from the 1 number

available in each direction. A sufﬁcient number of paths are required

to allow the pressure waves to be modelled with accuracy.

Solutions can be found at each point where opposing Cþ and C

characteristics intersect. Values of quasi-invariants Jþ and J are

established from earlier locations on each characteristic. The process

of solution starts from some set of known ﬂow conditions thoughout

the network. These ‘initial’ conditions may be either a static or

steady ﬂow state or even transient ﬂow conditions which may have

been determined from a previous simulation.

C– characteristics

dx/dt = V – a

C+ characteristics

dx/dt = V + a

Limits of region

influenced by P

Typical intersections

Limit of region upon

which P depends

Fig. 5.2. Characteristics in the x—t plane

Application of characteristic equations