Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour

Подождите немного. Документ загружается.

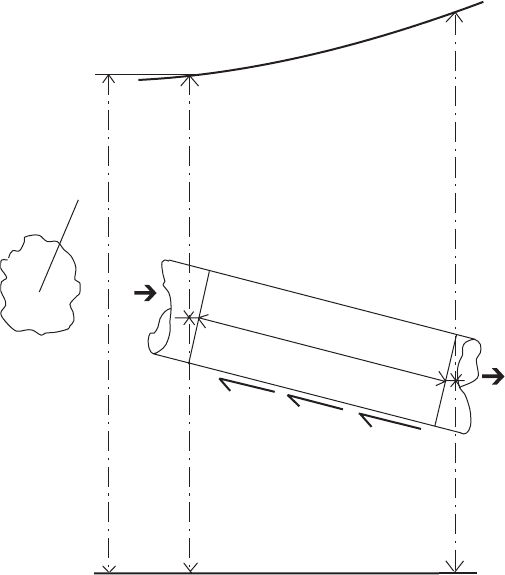
the valve to be closed at some rate that caused ﬂow to decelerate at

a rate dV=dt and producing an inertial head rise H

at the upstream

valve face. Forces acting upon the body of liquid contained in the

pipeline are:

Pipeline resistance ¼gAhf ¼gAfLV

=ð2gDÞ

Force imposed at the valve face ¼gAH

Inertia force ¼AL dV=dt

where g is acceleration due to gravity and f is a friction factor.

Summing these forces and dividing throughout by gA gives:

fLV

=ð2gDÞþL=g dV=dt þ H

¼ 0 ð2:1Þ

Neglecting pipeline resistance produces the simple relationship:

¼L=g dV=dt ð2:2Þ

This simple expression can be used to obtain a very rapid assessment of

transient pressure rise/fall for a given rate of ﬂow change. Supposing a

valve closure at the downstream end of the pipeline occurs. As soon

as the valve has become completely closed then V ¼ 0 and

dV=dt ¼ 0; that is, no further change in velocity occurs. The inertial

head H

becomes zero and the transient event is over. The limitation

of this approach arises when the magnitude of dV=dt is large and/or

the pipeline length L is considerable. Then values of H

can become

unrealistically large and it is at this stage that it is necessary to

employ the elastic approach in order to obtain more realistic answers.

The incompressible ﬂow equation (2.1) has another important function

Valve closing

Static head line

Inertial head gradient

Resistance gradient

Velocity = V

Diameter = D

Cross-section A

Fig. 2.1. Deﬁnition sketch for rigid column analysis

Pressure transients in water engineering

in that it can be used to provide preliminary estimates for capacity of

some types of surge protection equipment and some examples of its

use in this regard will be considered later in this book.

2.2 Compressible ﬂow theory

A straightforward derivation of the equations of motion in compressible

ﬂow is presented in this chapter. Basically there are two independant

variables: x, the distance along the axis of a pipeline; and t, the time

which has elapsed from some starting-point. The distance along a pipe-

line may be þve or ve depending upon how the user has decided to

schematise a network but the normal ﬂow direction in a line would

be taken as the þve direction. The time elapsed may also be fairly

arbitrarily assigned. For instance time t ¼ 0 might be taken at or

shortly before a transient event commences.

Dependent variables are fundamentally those of ﬂow rate Q and

pressure p. These vary with both x and t. Assuming a uniform velocity

V over any pipe cross-section A then velocity can replace ﬂow rate

through V ¼ Q=A. The relationships governing these variables are

those of conservation of mass and conservation of force and

momentum. Other variables such as air volume, water level or possibly

pump speed are related to the primary variables V and p through

additional equations.

2.2.1 Conservation of force

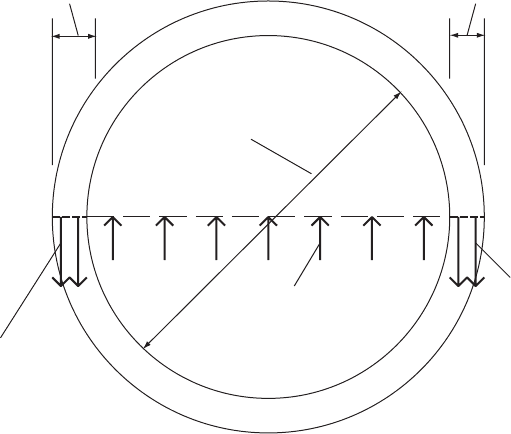
Consider a section of pipeline having an arbitrary shape of cross-section

A and of length dx as illustrated in Fig. 2.2. At any instant the forces

acting upon the body of liquid within this element are:

the net pressure force ¼@p=@x dxA

the pipeline resistance force ¼S dx gA

the axial component of liquid weight ¼@z=@x dx  gA

and the inertia force ¼A dxð@V=@t þ V @V=@xÞ

where S is the rate of head loss due to pipeline resistance,  is liquid

density, g is acceleration due to gravity and z is elevation of the pipe

centreline.

Summating these forces:

 @p=@x dxA S dx gA  @z=@xgA

 A dxð@V=@t þ V @V=@xÞ¼0

Derivation of basic equations

and dividing throughout by A dx gives:

1=  @p=@x þ gS þ g @z=@x þ @V=@t þ V @V=@x ¼ 0 ð2:3Þ

2.2.2 Conservation of mass

Considering the mass balance within the element over an increment of

time, dt:

the net mass inﬂux to the element (neglecting second-order effects)

¼A @V=@x dx  V @A=@x dx  VA @=@x dx

the rate of change of mass within the element

¼ @=@tðA dxÞ¼@A=@t dx þ A @=@t dx

Piezometric line

Horizontal datum

z + ∂z/∂x dx

rAV + ∂(rAV )/∂x d

h = p/(rg)

p/(rg) + ∂[p/(rg)]/∂x dx

rAV

Fig. 2.2. Deﬁnition sketch for compressible ﬂow analysis

Pressure transients in water engineering

Equating net mass inﬂow to rate of change of mass within the

element yields:

A @V=@x dx þ V @A=@x dx þ VA @=@x dx þ @A=@t dx

þ A @=@t dx ¼ 0

and dividing throughout by the mass of ﬂuid within the element A dx

gives:

@V=@x þ 1=ð@=@t þ V @=@x Þ

þ 1=Að@A=@t þ V @A=@xÞ¼0 ð2:4Þ

2.2.3 Compressible ﬂow equations in terms of total head H

Introducing pressure head h ¼ p=ðgÞ and total head above datum

H ¼ h þ z then the force balance equation:

@V=@t þ V @V=@x þ 1=  @p=@x þ gS þ g @z=@x ¼ 0 ð2:3Þ

becomes:

@V=@t þ V @V=@x þ 1=ðgÞð@H=@x  @z=@xÞþgS þ g @z=@x ¼ 0

or ﬁnally:

@V=@t þ V @V=@x þ g @H=@x þ gS ¼ 0 ð2:5Þ

In the mass balance equation:

@V=@x þ 1=ð@=@p  @p=@t þ V @=@p  @p=@xÞ

þ 1=Að@A=@p  @p=@t þ V @A=@p  @p=@xÞ¼0 ð2:2Þ

Since  and A are taken to be solely dependant on pressure p, therefore,

d=dp ¼ @=@p and dA=dp ¼ @A=@p. Also dz=dx ¼ @z=@x since @z=@t

is assumed ¼ 0.

Substituting gðH  zÞ for pressure p then:

@V=@x þf1=  d=dp þ 1=A  dA=dpggf@H=@t þ V @H=@xg

f1=  d=dp þ 1=A  dA=dpgg dz=dx ¼ 0

Writing,

1=a

¼ ð1=  d=dp þ 1=A  dA=dpÞ

Derivation of basic equations

or,

a ¼ 1=

fð1=  d=dp þ 1=A  dA=dpÞg ð2:6Þ

then the mass balance equation ﬁnally becomes:

a @V=@x þ g=af@H=@t þ V @H=@xgg=aV dz=dx ¼ 0 ð2:7Þ

Pressure transients in water engineering

Interpretation of a

A critical element of the equation of conservation of mass (equation

(2.7)) derived in Chapter 2 is the quantity a which is a complicated

function involving both the properties of the ﬂuid and of the conduit.

The value assigned to this parameter will have a crucial role to play

in the prediction of pressure extremes. This chapter attempts to

describe some of the factors which should be considered when choosing

a value and also some of the uncertainties present in estimation.

In Chapter 2 the quantity a was established as:

a ¼ 1=

fð1=  d=dp þ 1=A  dA=dpÞg ð2:6Þ

The value of a is dependent upon the properties of the ﬂuid  and d=dp

and upon the cross-sectional area of the conduit and its deformation

characteristics A and dA=dp.

3.1 Fluid properties

Considering ﬂuid characteristics. For water in the liquid state, the bulk

modulus K is deﬁned by:

K ¼ dp=ðd=Þ or 1=K ¼ 1=  d=dp ð3:1Þ

For water, the value of K varies only slowly with temperature with a

decrease of the order of 2% between 08C and 508C. A value of

2.137 GN/m

at 218C is given by Knapp et al. (1970) with Thorley

and Enever (1979) providing a slightly higher value of 2.193 GN/m

at 208C. Seawater has a value of 2.4 GN/m

at 258C. For a computer

simulation conducted assuming an almost uniform temperature, K

can be considered constant and independent of ﬂow conditions. If it

is assumed that the body of water is inﬁnitely large then:

a ¼ 1=

fð1=  d=dp þ 1=1dA=dpÞg or a ¼

fK=g

ð3:2Þ

Equation (3.2) is the speed of propagation of sound or of a pressure

wave through an unconstrained body of water. Equation (2.6) repre-

sents the speed of the pressure wave or sound wave through a ﬂuid

body which is contained within a conduit.

3.2 Inﬂuence of the conduit wall

Introduction of the term 1=A  @A=@p represents the inﬂuence of the

conduit containing the water. The simplest representation of the

pipeline’s effect on a is that for a relatively thin-walled circular elastic

pipe which is unconstrained in the axial direction. With reference to

Fig. 3.1, if a change of internal pressure dp takes place, then for

equilibrium:

dpD ¼ d2s or d ¼ D dp=ð2sÞ

Change of internal

pressure = dp

Wall thickness = s Wall thickness =

Diameter = D

Change of hoop stress = ds

Fig. 3.1. Forces at a pipe cross-section

Pressure transients in water engineering

also

Youngs modulus E ¼ d=ðdc=cÞ¼dpD=ð2s dD=DÞ

¼ D

=ð2sÞdp=dD

assuming that the pipe is entirely free to contract in length. Re-

arranging,

dD=dp ¼ D

=ð2sEÞ

Cross-sectional area A ¼ =4D

and A þ dA ¼ =4ðD þ dDÞ

,or

neglecting second-order effects:

dA ¼ =2D dD or dA=dD ¼ =2D

and

1=A  dA=dD ¼ 2=D

then,

1=A  dA=dp ¼ 1=A  dA=dD  dD=dp ¼ 2=D  D

=ð2sEÞ

¼ D=ðsEÞð3:3Þ

3.3 Simple expression for a

Substitution of the relationships of equations (3.1) and (3.3) in the

expression for a then:

a ¼ 1=

f½1=K þ D=ðsEÞg

To accommodate these conditions in which the pipe is not entirely

free to contract longitudinally due to restraint, a factor c

is introduced

so that ﬁnally:

a ¼ 1=

fð1=K þ Dc

=ðsEÞÞg or

a ¼

ðK=Þ=

ð1 þ DK=ðsEÞc

Þð3:4Þ

The speed of propagation of the pressure wave through an uncon-

ﬁned body of liquid is modiﬁed by the effect of the containing pipe

walls. In all cases a reduction in the unconﬁned value for

a ¼

ðK=Þ is experienced. Liquid and pipe are considered to act as

a composite medium giving a single value of a for this two-component

arrangement. This is justiﬁed by the continuous coupling action

between liquid and conduit throughout the system. Calculations can

be carried out for a pipeline system modelled with the liquid and

Interpretation of a

pipewall represented as separate components using individual propaga-

tion rates for liquid and conduit but these are usually conﬁned to the

analysis of vibrations. Some examples of these types of analyses are

described in papers by Ellis (1980), Kot et al. (1980), Wilkinson

(1980) and Heinsbroek and Tijsseling (1994). These methods are not

used in day-to-day pressure transient investigations.

For the simple case considered, wave speed a is seen from equation

(3.4) to be a constant for each pipeline of a system, independent of

ﬂow conditions. Individual values of a used in analyses can vary consid-

erably from case to case depending upon the geometrical characteristics

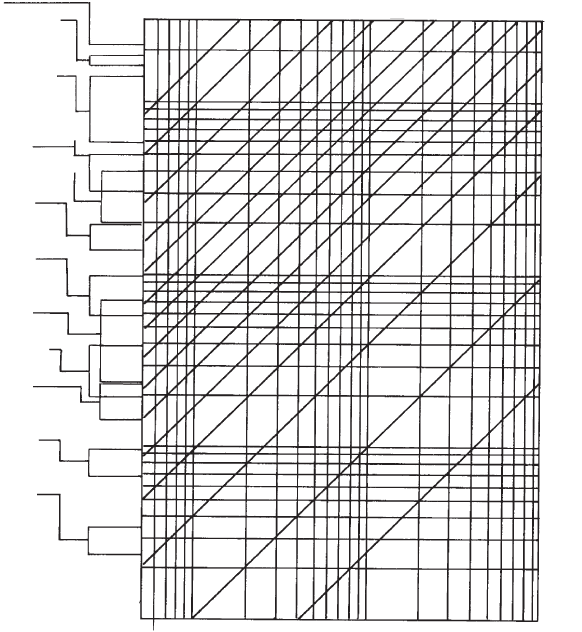
of the pipe and its material. Figure 3.2 displays the possible range in

wave speed as a function of elastic modulus E and the ratio Dc

=s for

500

400

300

200

100

321

a = 1350 1300

Steel

Hard cast iron

Soft cast iron

Concrete

Asbestos cement

Polyester

(glass fabric)

Polyester

(glass fibre)

Perspex

PVC (hard)

PVC

(blow resisting)

PE (hard)

PE (soft)

log

(E)

1200 1100 1000 900 800 700 600

log

(Dc

/s)

a = ÷ (K/r)/÷[1 + DKc

/(sE )]

Fig. 3.2. Acoustic wave speed a as a function of E and Dc

Pressure transients in water engineering

a circular pipe section. A wave speed value for wood stave pipe was

given by Fedosoff and Szpak (1979) as 762.0 m/s. The inﬂuence of

constraints has been considered by various authors such as Streeter

and Wylie (1967), Thorley and Enever (1979) and Jaeger (1977).

Expressions for the constraint factor c

for different circumstances,

including thick-walled conduits deﬁned by D=s < 25, and tunnels

have been included in Table 3.1.

Table 3.1. Constraint factor c

for various conditions

Pipelines: a ¼

ðK=Þ=

ð1 þ D=s  K=E  c

Thin-walled: D=s  25 Thick-walled: D=s < 25

Anchored at one end and

other end free

¼ 5=4   c

¼ D=ðD þ sÞð5=4  Þþ2s=Dð1 þ Þ

Anchored at both ends

¼ 1  

¼ D=ðD þ sÞð1  

Þþ2s=Dð1 þ Þ

Expansion joints

¼ 1  =2

Expansion joints

throughout

¼ 1 c

¼ D=ðD þ sÞþ2s=Dð1 þ Þ

is usually in the range 0:85  c

 1:25

Tunnels: a ¼

ðK=Þ=

ð1 þ K=Ec

Unlined: E ¼ E

¼ 2ð1 þ Þ

Lined: E ¼ lining modulus, E

¼ rock modulus

¼ 1=ð1 þ

D=s  E

=EÞ

Interpretation of a