Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour

Подождите немного. Документ загружается.

3.4 Variation of a with conduit shape

In the case of other cross-sectional shapes such as square ducts for

instance, matters are complicated by deformation from the original

shape under atmospheric conditions, as pressure is increased or

decreased. Thorley and Enever (1979) provide extensive information

on propagation speeds for a range of conduit shapes. The wave speed

remains constant for a given shape of liquid-ﬁlled pipe and a speciﬁc

value of D=s. They show a general equation for polygonal ducts:

1=A  dA=dp ¼ 1=EfD=s þ tan

ðD=sÞ

=15g

þ tan

ðD=sÞ=ð2GÞð3:5Þ

where  is the angle between ﬂats, D is the distance between the ﬂats, s

is wall thickness and G is the shear modulus of pipe wall material. It will

be noted that as the number of ﬂats approaches 1 the shape becomes

increasingly circular,  tends to zero and the expression 1=A  dA=dp

approaches D=ðsEÞ.

3.5 Inﬂuence of gas on a

Thus far the composite wave speed a has remained independent of ﬂow

conditions. Gases are present in the majority of liquids, both as free gas

in the form of bubbles and also as dissolved gas. As pressure is increased,

the amount of gas which can be dissolved also increases, thus reducing

the initial amount of free gas. According to Knapp et al. (1970),

dissolved gas has a negligible effect upon the tensile strength of a

liquid and thus will not signiﬁcantly inﬂuence the acoustic wave

speed. However, the presence of free or undissolved air or gas within

the liquid body introduces a further component to the composite

medium which does have an important inﬂuence upon speed of pressure

waves. Deformation of the liquid—gas mixture with changing pressure is

greatly inﬂuenced by the much greater compressibility d

=dp of the gas

with 

representing the gas density.

If a mixture of gases is in contact with the liquid surface, Henry’s law

states that the amount of each gas that will dissolve at equilibrium is

governed by its partial pressure. This can be written as: m

¼ p

where m

is the mass of gas dissolved/unit volume of liquid,  is a

temperature-dependent solubility constant and p

is equilibrium

partial gas pressure (bar). Under conditions just described, maximum

or saturation concentration of air in water at normal temperature and

atmospheric pressure is just under 2%, of which one-third is oxygen

Pressure transients in water engineering

and two-thirds is nitrogen. Although its solubility is high, the amount of

dissolved is very low since air contains only 0.03% of this gas. The

maximum air content < saturated concentration unless special treat-

ment has been carried out.

If pressure should fall, the liquid becomes supersaturated with gas for

that pressure and so some dissolved gas is released from solution

although it usually takes several seconds for a new equilibrium to be

reached. During a short-lived transient event equilibrium may not be

achieved. Gas release rate is greater than the corresponding gas absorp-

tion rate and so there is a net amount of free gas in the form of bubbles.

This release of gas is termed ‘gaseous cavitation’. If pressure drops below

the saturation pressure of liquid vapour, a very fast release occurs

termed vaprous cavitation within a few micro-seconds.

Expressing dissolved gas mass as an equivalent volume of gas Vol

under atmospheric pressure and at 08C, the following relationship is

obtained:

Vol

=Vol

¼ p

=1:013

where Vol

is liquid volume,  is a solubility constant in units of volu-

metric concentration ¼0.0187 for air at 208C. Void fraction 

can be

written:



¼ Vol

=ðVol

þ Vol

provided no slippage is assumed between bubbles and ﬂowing liquid.

The notation 

is proportional to absolute pressure. If saturated void

fraction 

is about 2% at atmospheric pressure p

atm

, then at

atm



¼ 1% with the other 1% having come out of solution and

become free gas. As pressure drops, free bubbles of gas expand following

the gas law, aided in their growth by gas evolving from the now super-

saturated liquid and diffusing into the bubbles. Eventually a bubble

reaches a critical diameter when the differential pressure across the

bubble wall exceeds the surface tension force. Explosive growth in

bubble size then occurs with bubbles starting to rise towards the

crown of the pipe. Since the void fraction was related to a speciﬁc pres-

sure, usually atmospheric pressure, any gas which comes out of solution

at a lower pressure will have a volume given by the gas law:

abs

Vol



¼ constant

where  is the ratio of speciﬁc heats for the gas and Vol

is the amount of

free or undissolved gas. Then, if the amount of gas coming out of

solution is 

and the initial amount of free gas is 

, both being

Interpretation of a

measured at atmospheric pressure p

atm

, then at some pressure p

abs

the

volume fraction  will be:

 ¼ð

þ 

Þðp

atm

abs

ð1=Þ

It takes a ﬁnite time for a new equilibrium condition to become estab-

lished and so the amount of gas evolving from solution 

will not

immediately be the total amount for the pressure p

abs

. The rate at

which gas is released from solution is dependent upon a number of

factors. Dissolved gas can only appear from solution if a ‘free phase’

boundary exists. This requires the presence of interstices in conduit

walls where free gas can lodge and/or particles within the liquid

which can act as ‘hosts’ for bubbles of free gas. Crevices and small

cracks in pipe walls are found, also micro-nuclei within the ﬂow.

Keller and Zielke (1976) carried out ﬁltering and rinsing of test

apparatus with ﬁlter size 0.5 mm. Despite this they found an average

of 2.8 nuclei/cm

with particles as large as 120 mm present. It is a

practical impossibility to completely clean pipes and tunnels of dust

particles. Turbulence can also inﬂuence the rates of gas release from

solution and some observations have shown that as Reynold’s

number (Rn) increases, the rate of release also rises and the time for

bubble content to stabilise falls. For an Rn of 370 000, bubble content

stabilises after 9 s whereas if Rn ¼ 590 000, bubble content is stabilised

after 5—6 s. Since the gas release rates depend on a range of factors, it is

not surprising to ﬁnd alternative approaches being used by different

modellers. For example, Fox (1977) assumed that all dissolved gas

evolved from solution with no delay and that the liquid was initially

saturated with 2% gas at atmospheric pressure. Other investigators

have adopted an exponential gas release rate. What has been noted

is that including some air produces essentially the same result and

predictions were not very sensitive to the initial free gas content,

release rate or amount of gas released.

To illustrate the inﬂuence of free gas upon behaviour of the pressure

wave consider a liquid having total void fraction  at the prevailing

absolute pressure p

abs

. Let the gas density be 

with liquid density .

If the volume of free gas is Vol

and volume of liquid is Vol

, total

volume Vol ¼ Vol

þ Vol

. Mean density of the mixture 

is given by:



¼ð

Vol

þ Vol

Þ=Vol



¼ 

þð1  Þ

Pressure transients in water engineering

Compressibility of liquid is represented by:

1=K ¼ 1=  d=dp

and compressibility of gas by:

1=K

¼ 1=

 d

=dp

Compressibility of the mixture can then be represented by:

=K

þð1  Þ=K

Substituting in the expression for wave speed a then for a circular pipe

section:

a ¼ 1=

f

½Dc

=ðsEÞþ=K

þð1  Þ=Kg ð3:6aÞ

Essentially the same equation has appeared in a number of guises.

Martin et al. (1976) assumed the contribution of the gas fraction to

mixture density was small and so:



ð1  Þ

giving

a ¼ 1=

fð1  Þ½Dc

=ðsEÞþ=K

þð1  Þ=Kg ð3:6bÞ

Tullis et al. (1976) assumed void fraction to be small giving

1    1 so that for a thin-walled pipe free to contract in length:

a ¼ 1=

fðD=ðsEÞþ=K

þ 1=KÞg ð3:6cÞ

The compressibility of gas represented by K

can be replaced as follows.

Applying the gas law to a ﬁxed mass of free gas then:

abs

Vol



¼ constant

where  ¼ C

is the ratio of speciﬁc heats for the gas, C

is speciﬁc

heat at constant pressure, and C

is speciﬁc heat at constant volume.

All diatomic molecules of gas display the same value of  ¼ 1:4at

moderate temperatures applicable for pipeline transients. Texts on

thermodynamics will yield additional details, for example Spalding

and Cole (1963). Differentiating with respect to Vol

then,

abs

=dVol

¼ constant=Vol

ð1 þÞ

abs

¼ dVol

=Vol

Also the mass of gas is given by:



Vol

¼ constant

Interpretation of a

Again, differentiating with respect to Vol

d

=dVol

¼constant=Vol

¼

=Vol

and rearranging,

d

=

¼dVol

=Vol

therefore,

abs

¼  d

=

Gas compressibility is thus represented by:

1=K

¼ 1=

 d

=dp

abs

¼ 1=ðp

abs

Þðdp

abs

=dp

abs

Þ¼1=ðp

abs

Making these substitutions the equation for wave speed is then:

a ¼ 1=

f½ð1  Þ þ 

½Dc

=ðsEÞþ=ðp

abs

þð1  Þ=Kg ð3:7Þ

Fox (1977) neglected the gas mass contribution to mean density,

giving, 

ð1  Þ and assumed 1    1 in the liquid compressi-

bility term, also  ¼ 1:0, thus yielding the simpler expression:

a ¼ 1=

fð1  Þ½D=ðsEÞþ=p

abs

þ 1=Kg ð3:8Þ

This form of the equation for a perhaps highlights the fact that wave

speed is dependent upon absolute pressure p

abs

or has become a

function of the prevailing transient ﬂow condition where free gas is

considered as a constituent of the ﬂuid in the pipeline. Without the

inﬂuence of gas, the wave speed remains constant and independent

of ﬂow conditions for a speciﬁed pipeline.

Acoustic velocity a is strongly dependent on void fraction . Even a

small amount of free gas produces a dramatic fall in wave speed. At the

opposite end of the scale, as void fraction tends to 100%, the wave

speed rises towards the speed of sound in air given by:

a ¼

fp

abs

=

Adopting standard values at atmospheric pressure and ambient

temperature, 

¼ 1:22506 kg=m

, p

atm

¼ 101:3kN=m

and  ¼ 1:4,

then the speed of sound in air is calculated as 340 m/s.

The gas release head is considered to be around 2.4 m absolute (Fox,

1977). Once the gas has evolved from solution it is more difﬁcult to

force it back into solution by a simple rise to atmospheric pressure

and requires a more substantial pressure increase before much of the

gas will be forced to redissolve. Fox proposed that all gas came out of

Pressure transients in water engineering

solution at this gas release head and that equilibrium concentration was

achieved with no delay. Other modellers have adopted an exponential

decay of rate of gas release.

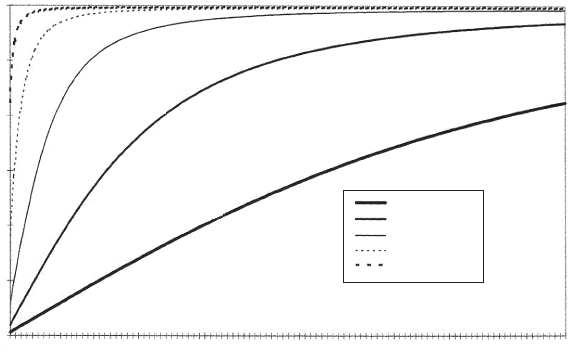
Figure 3.3 shows how wave speed changes with pressure for a range of

free gas concentrations. The gas fractions are those at atmospheric

pressure and range from 0.0001% to 1.0% by volume.

Adoption of a wave speed which varies with changing pressure

conditions within each pipeline of a network has important implications

with regard to the way in which computations are conducted. In the

presence of free gas the liquid in the pipeline system over most of the

range in free gas concentration has effectively become a ﬂuid which

retains a density dominated by the weight of the liquid component

but with compressibility more like that of the gas. Only at the extremi-

ties of concentration range does this alter, with liquid properties

dominant when only very small amounts of gas are present, and gas

properties dominant if only quite small amounts of liquid are available.

Evolution of gas from solution and subsequent expansion of the free

gas has the effect of introducing an additional source of ﬂuid to the

system. Suppose that upstream of a region in which free gas is present

and expanding, the ﬂow is decelerating at some rate dV=dt. Down-

stream of the zone of gas expansion the ﬂow will be decelerating at a

lesser rate as the ﬂow from upstream will be augmented by liquid

released from the length of pipe containing the expanding gas in

0.1

0.5

0.9

1.3

1.7

2.1

2.5

2.9

3.3

3.7

4.1

4.5

4.9

5.3

5.7

6.1

6.5

6.9

7.3

7.7

8.1

8.5

8.9

9.3

9.7

10.1

Pressure (bar(abs))

Wave speed (m/s)

1200

1000

800

600

400

200

= 1%

= 0.1%

= 0.01%

= 0.001%

= 0.0001%

Fig. 3.3. Acoustic wave speed plotted against pressure for various void fractions

Interpretation of a

order to accommodate the increasing gas volume. The effect is to

reduce the downstream rate of deceleration and suppress to a signiﬁcant

extent further pressure drop.

The equation for wave speed a in the presence of a free gas consti-

tuent has been developed on the basis of a homogeneous dispersal of

gas. Observations have revealed a large number of gas/liquid ﬂow

regimes with no standard deﬁnition for each type of ﬂow. Escarameia

(2005) mentions that up to 84 different terms have been in use and

illustrates some of the ﬂow patterns for both horizontal and vertical

movement.

The present analysis has neglected ‘slip’ velocity between gas and

liquid and this can have signiﬁcant implications in some circumstances.

Consider a descending section of pipeline carrying a range of bubble

sizes. The larger bubbles will tend to move more slowly — that is,

have a larger slip velocity than smaller bubbles. The smaller bubbles

will catch up and be absorbed by larger bubbles, resulting in still

larger and slower-moving bubbles. The large bubble may eventually

come to rest and start to move back upstream, collecting yet more

small bubbles and causing variations of void fraction not accommodated

in the simple theory presented. This type of behaviour can also result in

a pulsating type of ﬂow behaviour.

A further departure arises when a gas/liquid regime such as the ‘slug’

ﬂow approaches a local source of head loss such as a valve. The loss in

pressure, p, across the valve is given by:

p=ð

g Þ¼K

=ð2gÞ

When the mixture is predominantly liquid, 

will be close to the

liquid density and p will be relatively large. If a ‘slug’ of gas should

arrive at the valve, the mixture density will fall and pressure drop p

will also drop proportionately, causing a pressure wave to propagate

from the valve into the pipeline. This process will occur each time a

‘slug’ of gas passes through the valve. This phenomenon is not accom-

modated by the straightforward theory.

3.6 The effect of sewage

Sewage is a generic term including the following:

. soil or sanitary sewage from households

. industrial wastewaters

. cooling water or ‘thermally’ contaminated water

Pressure transients in water engineering

. surface water from rainfall and storm water

. drainage water from building sites, ﬁelds and leakage from broken

pipes.

The temperature of sanitary sewage tends to be relatively uniform all

year round, usually between 108C and 218C. From 300 mg/l to 500 mg/l

of dissolved solids and 200 mg/l to 400 mg/l of suspended solids

including grease will have been added. Septic sanitary sewage may

under some circumstances produce hydrogen sulphide, which can be

corrosive to cement products such as concrete and asbestos cement

pipes. Industrial wastewater can vary considerably in temperature and

other physical characteristics and ranges from strongly acid to strongly

alkaline, requiring special materials for pipelines, pumps and ﬁttings.

Dissolved and suspended solids may conceivably affect the density

and viscosity of the ﬂuid. Where solid particles or larger aggregations

of matter are present in sewage this adds a further component to the

medium. Depending upon the density and compressibility of this

material carried along in the liquid there may be an effect upon the

acoustic wave speed. Generally, with both a free gas component and

solid matter present, then the average density of the medium will be:



¼ðVol

þ 

Vol

þ 

Vol

Þ=ðVol

þ Vol

if Vol

þ Vol

¼ Vol

, Vol

=Vol

¼  and Vol

=Vol

¼ 

then:



¼ð1    

Þ þ 

þ 



Average compressibility becomes:

ð1    

Þ=  d=dp þ 

=

 d

=dp þ 

=

 d

=dp

¼ð1    

Þ=K þ =K

þ 

¼ð1    

Þ=K þ =ðp

abs

Þþ

then

a ¼ 1=

f

½ð1    

Þ=K þ =ðp

abs

þ 

þ Dc

=ðsEÞg ð3:9Þ

The manner in which K

changes with pressure will depend upon

constituents of the sewage. If compressibility is relatively low, like

water, then 

 constant.

Some efﬂuent pipelines are designed to convey sewage of a particular

type, for example from a residential area, and the solids content may be

assessed on this basis. Other lines may carry mixtures having a wider

Interpretation of a

range of properties from domestic and industrial wastes to stormwater

ﬂows. Properties of the mixture will vary signiﬁcantly and it is recom-

mended that investigations should include properties of stormwater

when ﬂows may well be at a maximum. Under dry weather conditions,

primarily domestic and/or industrial waste waters may be carried. While

mean daily ﬂows may be relatively modest, these may be conveyed in

the form of intermittent ‘plug’ ﬂows in which discharge rates are close

to the pumps’ duty point. It may well be necessary in such circum-

stances to investigate ﬂows involving different mixture properties.

Pressure transients in water engineering

Characteristic equations

Chapter 3 discussed how the acoustic wave speed in a pressure pipeline

system can be inﬂuenced by the properties of both the pipeline and by

any inclusions in water being conveyed. As far as sewerage systems are

concerned, a large part of the function of the water is to carry contami-

nants and impurities to treatment or disposal and it is to be expected

that both gas and some solid constituents will be present. This

chapter uses the partial differential equations together with the acoustic

wave speed a, to develop what are known as characteristic equations.

4.1 Development of characteristic equations

The force balance equation was derived in Chapter 2 as:

@V=@t þ V @V=@x þ g @H=@x þ gS ¼ 0 ð2:5Þ

and the equation balancing mass ﬂow and storage became:

a @V=@x þ g=af@H=@t þ V @H=@xgg=aV dz=dx ¼ 0 ð2:7Þ

It is possible to proceed directly to the solution of pressure transient

ﬂow problems using the above equations. However, many existing

modelling tools employ what are known as the ‘characteristic’ equations

and a simple derivation of these equations from the basic force and

mass balance equations (2.5) and (2.7) follows. These characteristic

equations have been used throughout this book to illustrate various

aspects of pressure transient behaviour.

Adding equations (2.5) and (2.7) balancing force and mass ﬂow then:

@V=@t þðV þ aÞ@V=@x þ g=að@H=@t þðV þ aÞ@H=@xÞ

þ gS  g=aV dz=dx ¼ 0