Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour
Подождите немного. Документ загружается.

the external system through the action of pipeline resistance. This
causes the external value propagating along the characteristic to be
quasi-invariant whereas the above analysis assumes invariant condi-
tions throughout.
6.8 Other bifurcation conditions
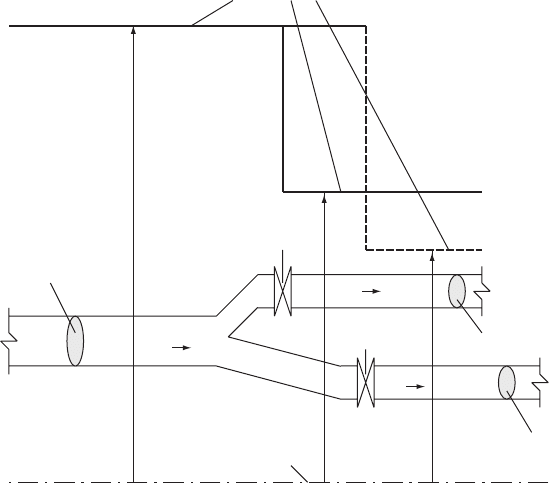
6.8.1 Bifurcation with operating valves
From time to time configurations may arise in which there is a choice
regarding how to model the feature. Consider the arrangement shown
in Fig. 6.14 which depicts a bifurcation. Just downstream of the
branch, valves are placed on each of the pipelines 1 and 2. These
valves may operate independently, one may be opening and the
other may be closing for instance. Assuming that there is negligible
separation between the bifurcation point and each of the valves,
then after each time step solution for the six unknowns H
1
, H
2
, H
3
,
V
1
, V
2
and V
3
should be obtained together. The equations necessary
82
Piezometric levels
Area = A
2
Area = A
3
H
3
H
2
V
2
H
1
Area = A
1
Valve 1
Valve 2
Common horizontal datum
V
1
V
3
Fig. 6.14. Bifurcation with operating valves
Pressure transients in water engineering
are:
V
1
g=a
1
H
1
¼ J
1
for pipe No. 1
V
2
g=a
2
H
2
¼ J
2
for pipe No. 2
V
3
g=a
3
H
3
¼ J
3
for pipe No. 3
H
1
H
2
¼ K
L1
V
2
2
=ð2gÞ for valve No. 1
H
1
H
3
¼ K
L2
V
2
3
=ð2gÞ for valve No. 2
A
1
V
1
A
2
V
2
A
3
V
3
¼ 0 at the bifurcation
where K
L1
and K
L2
are head loss coefficients for valves No. 1 and No. 2
respectively. This set of relationships contains two quadratic equations
and cannot be solved explicitly. An iterative solution is necessary for
each time step. Ellis and Tint (1976) described a method of solving
these equations.
An alternative to solving the complete set of equations together
using a specially constructed routine is to compromise and separate
the valves from the branch so that small increments x
i
are introduced
between the bifurcation and each valve with a corresponding small time
step t. Beyond each valve and on pipe No. 1, boundaries of the type
described in section 6.6 can be introduced allowing larger distance and
time increments to be used in the rest of the network. In this way
solutions can be found for the six unknowns using existing routines
and without introducing significant inaccuracies.
6.8.2 Isolating valves
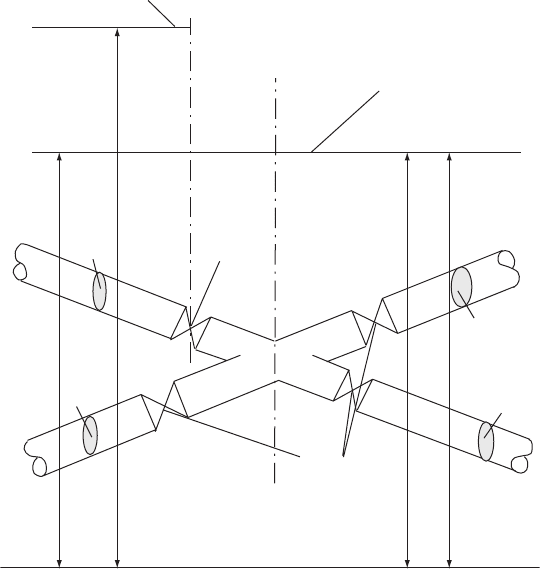
Distribution systems will usually be fitted with sluice valves on each
pipeline where it meets a connection point such as is illustrated in
Fig. 6.15. It may be necessary to analyse a number of conditions each
with certain parts of the distribution system isolated, with some of
the sluice valves closed. Rather than have to reconfigure the model
to suit each configuration, a single computation procedure can be
used to analyse all valve arrangements at a connection. Each valve at
a connection can be assigned a code number k
i
which is set to either
0 or 1. In the situation shown in Fig. 6.15, the valve on line 1 is shut
so k
1
¼ 0 while k
2
, k
3
and k
4
are all 1. The solution for common
junction head H at the connection is:
H ¼ 1=g
X
ðk
i
A
i
J
i
Þ=
X
ðk
i
A
i
=a
i
Þð6:28Þ
83
Boundaries
with the summation over all pipes. The head at the valve on each pipe is
then:
H
i
¼ H if k
i
¼ 1orH
i
¼a
i
=gJ
i
if k
i
¼ 0
Velocity at the valve on each pipeline i is then:
V
i
¼ J
i
ðÞg=a
i
H
i
6.9 Continuous drawoff
Within a distribution network there may be a large number of discrete
drawoff points — so many that it is not practical to model each point.
Options are to ‘lump’ a group of drawoffs into a single equivalent
large demand point. An alternative is to represent a set of demand
points along a pipeline as a continuous drawoff with distance. With
84
A
4
A
3
A
2
A
1
H
4
H
2
H
3
H
1
Piezometric line @ shut valve
Open valve
Shut valve
Common horizontal datum
Piezometric line @ open valve
Fig. 6.15. Isolating valves at a pipe junction
Pressure transients in water engineering
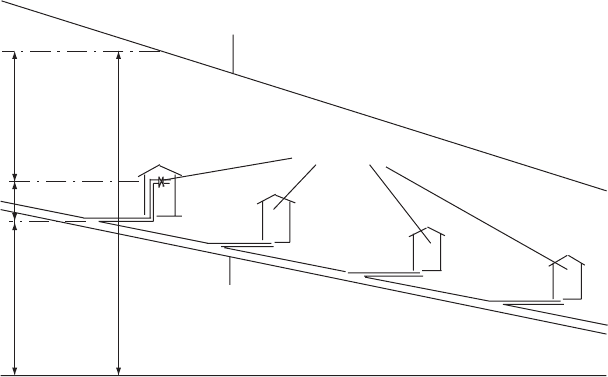
reference to Fig. 6.16, the discharge q
i
at any demand point i can be
written as q
i
¼ k
i
p
h
i
, with h
i
¼ H z z
i
. Along a pipeline total
drawoff q
t
is q
t
¼
P
ðk
i
p
h
i
Þ. The equivalent linear drawoff may be
written, q ¼ k
p
h ¼
P
ðk
i
p
h
i
Þ=L, with L being the length of pipeline.
Taking an average value of h
i
then, k ¼
P
k
i
=L.
Equation (2.4) representing conservation of mass within an element
of pipeline becomes:
@V=@x þ1 =f@=@t þ V @=@xgþ1=Af@A=@t þV @A=@xg
þ k=A
p
h ¼ 0 ð6:29Þ
The quasi-invariant relationships now become:
V g=aH ¼ J ðÞka=A
ð
p
h dt ð6:30Þ
The solutions for V and H at a pipeline node can easily be found.
Routines for solving the quasi-invarient equations with linear drawoff
along each pipeline, at pipe junctions where three or more pipes
meet, can also be set up.
The new term describing the drawoff effect can be approximated
along each segment of characteristic path. If there is no demand on a
pipeline then k ¼ 0 for that line. During a period of low demand k
can be set to a small value with k reaching a maximum during times
85
Common horizontal datum
h
z
z
i
H
Demand points
Pipeline
Piezometric line
Fig. 6.16. Distribution main with demand points
Boundaries
of peak demand. Figure 6.17 shows a pumped distribution system which
was modelled using this linear drawoff approach. Other applications
include irrigation systems where there are a large number of small
demand points.
86
PSV
Area 50R
Air valve at hi
g
h
p
oint on rin
g
main
Blank flange
Distribution area
Area 49R
Al Saad water storage compound
and pump house
Area 119R–122R
Pressure vessel
DN 300 ring main
Start of ring main
Distribution area Distribution area
Fig. 6.17. Typical distribution system
Pressure transients in water engineering
7
Valve closure in a simplified
system
The ‘elastic’ or compressible flow approach developed in the earlier
chapters allows more realistic values of inertial head rise to be estab-
lished. The price to be paid for these more acceptable head changes
is the development of elastic oscillations or vibrations within the pipe-
line system. These oscillations will generally persist until long after the
initial cause of the transient, for example a valve closure has been
completed. This chapter introduces the reader to the concept of
these vibrations in a pipeline system by examining an idealised simple
system.
A circumstance which has been used in a number of publications,
such as Streeter and Wylie (1967), Fox (1977) and Thorley and
Enever (1979), to illustrate the formation of elastic oscillations is the
case of a simple frictionless pipeline of uniform cross-section and
length L which runs between a reservoir and a fast-closing valve at
the opposite end of the line (Fig. 7.1). The positive flow direction is
assumed to be from the upstream reservoir to the valve.
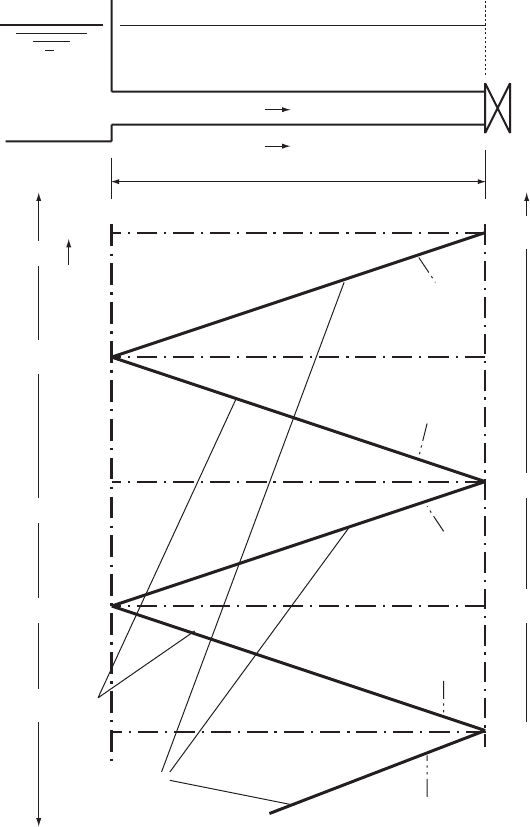
7.1 Instantaneous valve closure at t ¼ 0
Consider the body of liquid within the pipe to be made up of a series
of thin slices as shown in Fig. 7.2. Assuming the valve can be closed
in a short time, almost instantaneously, then the velocity of flow at
the valve face will be reduced to zero over the very short time of
closure. According to the method of characteristics, the invariant
value travelling towards the valve and arriving at the instant of
closure is:
V
o
þ g=aH
o
¼ Jþ
87
at the valve, V ¼ 0, so that:
Jþ¼g=aH (at the valve) or, H (at the valve)
¼ðV
o
þ g=aH
o
Þ=ðg=aÞ¼H
o
þ H
i
where H
i
¼ aV
o
=g is the inertial head rise.
88
Length = L
M
Level = H
o
Time +
t = 3L/a (seconds)
J+ = V
o
+ g/aH
o
J– = –V
o
– g/aH
o
J+ = –V
o
– g/aH
o
J– = V
o
– g/aH
o
J+ = V
o
+ g/aH
o
t = L/a (seconds)
H = H
o
t = 4L/a (seconds)
t = 2L/a (seconds)
t = 0 (seconds)
V = 0
Initial constant piezometric level = H
o
V
o
+X
Valve
C+ characteristics
C– characteristics
Fig. 7.1. Simple pipeline with fast-acting valve
Pressure transients in water engineering
At the instant of closure only a very thin layer of liquid, immediately
against the upstream face of the shut valve, will be brought to rest
ðV ¼ 0Þ and will be under the increased head ðH
o
þ H
i
Þ.
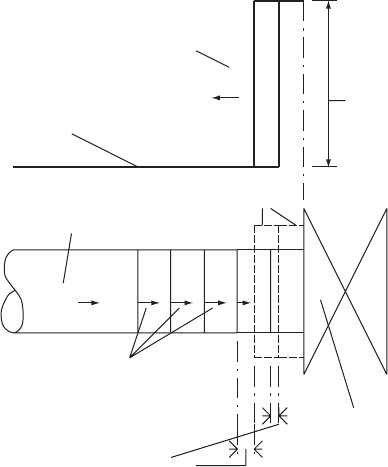
7.2 From 0 < t L=a
A short time later a further thin layer of liquid will be decelerated as it
meets the now stationary layer of liquid against the valve. Both layers
are not decelerated simultaneously as the second layer now has a
short distance to travel since the first layer is occupying a shorter
length of pipe (Fig. 7.2) on account of:
(a) having been compressed into a smaller volume under the increased
head H
i
(b) since the pipe wall has itself been distended giving an increased
cross-sectional area to accommodate the layer of stationary
liquid.
When the second layer of liquid is brought to rest its velocity is now
zero and pressure within the layer has increased by the inertial head rise
89
V
o
Static ‘layers’
Steady flow velocity
Additional travel of
first and second la
y
ers
‘Layers’ travelling towards valve
Valve abruptly closed
Inertial head rise = aV
o
/
g
Propagation rate of pressure wavefront = a
Steady flow piezometric line
Fig. 7.2. Representation of pressure wave progress
Valve closure in a simplified system
H
i
. Subsequent layers of liquid will be brought to rest in a similar
manner so that at some time t after valve closure the head rise H
i
will have reached a point x upstream of the valve. Since generally
V a then dx=dt a and x=t ¼ a. The invariant J propagating
upstream in the ve direction will have a value provided by the flow
conditions at the valve just after closure, that is:
J¼V g=aH or J¼0 g=aðH
o
þ H
i
Þ¼g=aH
o
V
o
The wave travelling upstream in the pipeline produces an increase in
internal pressure and is known as a ‘compression wave’. After a time
L=a the ‘pressure wave’ front will have reached the reservoir end of
the system. Characteristic paths as the wave travels upstream and is
then reflected back towards the valve are also shown in Fig. 7.1.
Up until time L=a, water has continued to flow into the pipeline from
the reservoir at velocity V
o
. At this time the entire liquid column within
the pipeline is now at rest ðV ¼ 0Þ under the head H
o
þ H
i
. The extra
volume of liquid now contained in the pipeline under the increased
pressure head H
i
is:
Volume ¼ V
o
AL=a
The state where the pressure head just inside the pipeline is greater
than the reservoir head by the amount H
i
is evidently unstable.
Again considering the characteristic arriving at the reservoir at this
time, then:
J¼g=aH
o
V
o
At the reservoir H ¼ H
o
(constant), therefore:
J¼V g=aH
o
¼g =aH
o
V
o
¼g=aðH
o
þ H
i
Þ
or
V ¼g=aH
i
¼V
o
7.3 L=a < t 2L=a
After the pressure wave reaches the upstream end of the pipeline, liquid
starts to flow back into the reservoir from the pipeline with velocity V
o
and head is reduced back to its original value H
o
. This effect initially
influences only the layer of liquid adjacent to the reservoir, but sub-
sequently successive layers of liquid are affected with a pressure wave
travelling along the pipeline from the reservoir towards the valve
with characteristic velocity, dx=dt ¼ a and producing a reduction in
90
Pressure transients in water engineering
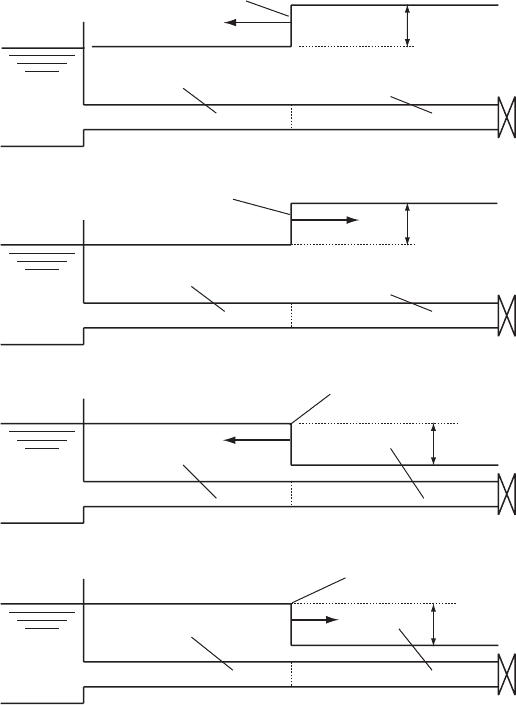
internal pipeline pressure. A wave which causes a reduction in pressure
is known as a ‘rarefaction’ wave.
The invariant travelling in the positive direction of flow along the
Cþ characteristic from the reservoir to the shut valve has a value
given by the conditions just found at the reservoir. Thus:
Jþ¼V þ g=aH ¼V
o
þ g=aH
o
After a total time 2L=a has elapsed from the initial valve closure, this
reflected pressure wave has now reached the shut valve. The invariant
91
H
o
a
H
i
M
(a) 0 £
t
£
L
/
a
Compression wave
V
= 0
V
=
V
o
H
o
a
H
i
M
Rarefaction wave
V
= 0
V
= –
V
o
(b)
L
/
a
£
t
£ 2
L
/
a
H
o
a
–
H
i
Rarefaction wave
M
(c) 2
L
/
a
£
t
£ 3
L
/
a
V
= 0
V
= –
V
o
H
o
a
–
H
i
Compression wave
M
V
= 0
V
= +
V
o
(d) 3
L
/
a
£
t
£ 4
L
/
a
Fig. 7.3. Pressure wave front at different stages following valve closure
Valve closure in a simplified system
