Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

278 4 Quantitative Analysis of Energy-Loss Data

if a Fourier log method is employed (Section 4.3.1), the background is removed

after deconvolution to yield the single-scattering core-loss spectrum J

EXELFS analysis is more straightforward if the data are recorded from a K-edge,

but for atomic numbers greater than 15 the K-loss signal is weak and therefore noisy,

so the L-edge may have to be used (Okamoto et al., 1991). In the case of transition

metals, an L

edge occurs within the energy range covered by the L

EXELFS and

must be removed from the experimental data, for example, by subtracting a suitably

chosen fraction of the intensity at energies above the L

threshold (Leapman et al.,

1981). For transition elements beyond Ti (Z = 22), the L

−L

splitting exceeds

5 eV, resulting in a “smearing” of the EXELFS, but this effect can be eliminated by

deconvolving J

with a pair of delta functions separated by the appropriate energy

and weighted by a suitable ratio (Leapman et al., 1982). This deconvolution can

be done by division of Fourier coefﬁcients, before, during, or after the removal of

plural scattering.

4.6.1.2 Isolation of the Oscillatory Component

The oscillatory part χ (E) of the core-loss intensity is obtained by subtracting from

(E) a smoothly decaying function A(E), representing the single-atom intensity

proﬁle. In general, A(E) is not available experimentally and cannot be calculated

with sufﬁcient accuracy, so it is obtained empirically by ﬁtting a smooth function

through J

,asinFig.4.20. This function should correctly follow the overall trend of

the data but not the EXELFS modulations themselves, otherwise false structure will

appear in the RDF at small values of radius r. An odd-order polynomial (Leapman,

1982) and a cubic spline (Johnson et al., 1981a) have been used. A power-law

Fig. 4.20 (1) Oxygen K-edge of sapphire, recorded using 100-keV incident electrons and collec-

tion semi-angle β =16 mrad. Also shown are (2) the extrapolated background intensity, (3) the

core-loss intensity after background subtraction, and (4) a smooth polynomial function A(E) ﬁtted

through the core-loss intensity. (A. J. Bourdillon, personal communication.)

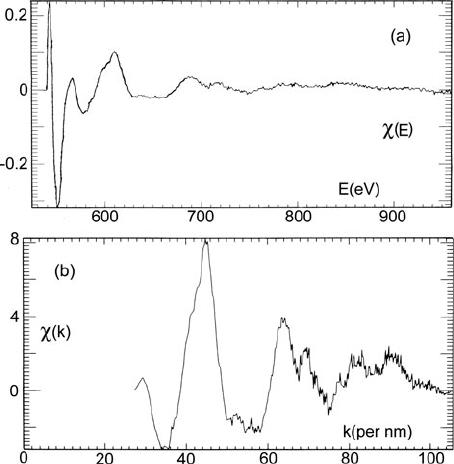
4.6 Analysis of Extended Energy-Loss Fine Structure 279

Fig. 4.21. (a) χ(E)and(b) k

χ(k), obtained from the data shown in Fig. 4.20

function may also be suitable if the exponent is allowed to vary somewhat with

energy loss (Stephens and Brown, 1981).

The difference spectrum is normalized by division with A(E)togive

χ(E) = [J

(E) − A(E)]/A(E) (4.75)

as shown in Fig. 4.21a. Deﬁning χ(E) as a ratio of intensities makes it unnecessary

to divide by an angular correction function (Section 4.2).

4.6.1.3 Scale Conversion

The energy scale of χ(E) is converted to one of wave number k of the ejected elec-

tron using Eq. (3.165). If energies are measured in eV and k in nm

−1

, the formula is

k = 5.123

√

kin

= 5.123(E −E

)

1/2

(4.76)

where E

kin

is the kinetic energy of the ejected inner-shell electron and E

is the

energy loss corresponding to E

kin

= 0. E

is not precisely the observed threshold

energy E

, since the latter corresponds to the excitation of electrons to the ﬁrst unoc-

cupied electron level. In a metal, this would be the Fermi level and in the absence of

exchange and correlation effects (Stern et al., 1980) one might expect E

= E

−E

280 4 Quantitative Analysis of Energy-Loss Data

In insulators, the initial excitation is often to a bound state (Section 3.8.5), for which

kin

< 0, leading to E

> E

. Because of possible chemical shifts, E

is best

obtained from the experimental spectrum; the inﬂection point at the edge or an

energy loss corresponding to half the total rise in intensity (Johnson et al., 1981a)

are possible choices. Unfortunately, an error in E

leads to a shift in the RDF peaks;

for the boron K-edge in BN, Stephens and Brown (1981) found that the r-values

changed by about 5% for a 5-eV change in E

In fact, the most appropriate value of E

is related to the choice of energy zero

assumed in calculating the phase shifts that are subsequently applied to the data.

Lee and Beni (1977) proposed treating E

as a variable parameter whose value is

selected, so that peaks in both the imaginary part and the absolute value (modulus) of

the Fourier transform of χ(k) occur at the same radius r. With suitably deﬁned phase

shifts (Teo and Lee, 1979), this method of choosing E

gave r-values mostly within

1% of known interatomic spacings (up to ﬁfth nearest neighbors) when applied to

EXAFS data from crystalline Ge and Cu (Lee and Beni, 1977).

Spectral data are usually recorded at equally spaced energy increments but after

conversion of χ (E)toχ( k), the data points are unequally spaced. If a fast Fourier

transform (FFT) algorithm is to be used, the k-increments must be equal and some

form of interpolation is needed. For ﬁnely spaced data points, linear interpretation

is adequate; in the more general case, a sinc function provides greater accuracy

(Bracewell, 1978). Some conventional (discrete) Fourier transform programs can

use unequally spaced χ(k) data.

4.6.1.4 Correction for k-Dependence of Backscattering

According to Eq. (3.167), the RDF is modulated by the term f

(k)/k, where f

(k)is

the backscattering amplitude. The χ (k) data s hould therefore be divided by this term.

A simple approximation is to take f

(k) ∝ k

−2

, based on the Rutherford scattering

formula: Eq. (3.3) with q =2k. As shown in Fig. 4.24, this provides a fair approxi-

mation for light elements ( e.g., C, O) but is inadequate for elements of higher atomic

number. In some EXAFS studies, χ(k) is multiplied by k

(as in Fig. 4.21b), the

value of n being chosen empirically to emphasize either the low-k or the high-k data,

and thus the contribution of low-Z or high-Z atoms to the backscattered intensity

(Rabe et al., 1980).

4.6.1.5 Truncation of the Data

Before computing the Fourier transform, values of χ (k) that lie outside a chosen

range (k = k

min

to k

max

) are removed. The low-k data are omitted because single-

scattering EXAFS theory does not apply in the near-edge region and because at low

k the phase term ϕ(k) becomes nonlinear in k. High-k data are excluded because they

consist mainly of noise (ampliﬁed by multiplying by k

,asinFig.4.21b), which

could contribute spurious ﬁne structure to the RDF. The occurrence of another ion-

ization edge at higher energy may also limit the maximum value of k. In typical

EXELFS studies (Johnson et al., 1981a; Leapman et al., 1981; Stephens and Brown,

4.6 Analysis of Extended Energy-Loss Fine Structure 281

1981), k

min

lies in the range 20–40 nm

−1

and k

max

in the range 60–120 nm

−1

.Iftoo

small a range of k is selected, the RDF peaks are broadened (leading to poor accu-

racy in the determination of interatomic radii) and accompained by satellite peaks

arising from the truncation of the data. These truncation effects can be minimized by

using a window function W(k) with smooth edges (Lee and Beni, 1977) or by choos-

ing k

min

and k

max

close to zero crossings of χ (k). When the limits have been suitably

chosen, the RDF should be insensitive to the precise values of k

min

and k

max

4.6.1.6 Fourier Transformation

The required Fourier transform will be deﬁned as follows:

(

)



∞

−∞

(

)

(

)

(

)

exp

(

2ikr

)

dk (4.77)

In practice, a discrete Fourier transform is used, so the variable k becomes πm/N

(see Section 4.1.1) and the limits of integration are m =0 and m =N, where N is

the number of data points to be transformed. If an FFT algorithm is used, N must

be of the form 2

, where y is an integer, in which case the χ (k) data may require

extrapolation to values of k larger than k

max

. A large value of N gives χ at more

closely spaced intervals of r.

In the Fourier method of EXAFS or EXELFS analysis, interatomic distances are

deduced directly from the positions of the peaks in the transform

χ(r). The rationale

for this procedure is as follows. Ignore for the moment the effect of the window

function and assume that the exponential and Gaussian terms in Eq. (3.167)are

unity, corresponding to the case of a perfect crystal with no atomic vibrations and

no inelastic scattering of the ejected core electron. We must also assume that the

phase shift ϕ

(k) can be written in the form

(k) = ϕ

+ϕ

k (4.78)

Substitution of Eqs. (3.167) and (4.78) into Eq. (4.77)gives

(

)



∞

−∞



sin

2kr

+φ

[

cos 2kr − i sin 2kr

]

dk (4.79)

The imaginary part of the Fourier transform is

)

(

)

∞

−∞

{sin(2kr)sin[k(2r

+φ

)] cos φ

+sin(2kr) cos[k(2r

+φ

)] sin φ

}dk

(4.80)

and is zero for most values of r, since the (modulated) sinusoid functions aver-

age out to zero over a large range of k. However, if r satisﬁes the condition

2r = 2r

+ϕ

282 4 Quantitative Analysis of Energy-Loss Data

)

=−

cos φ

∞

−∞

sin

+φ

−1

2π

cos φ

(4.81)

Im[

χ] therefore consists of a sequence of delta functions, each of weight propor-

tional to N

and located at r = r

+ ϕ

/2, where j = 1, 2, etc., corresponding

to successive shells of backscattering atoms. Likewise, Re[

χ] is zero except at

r = r

+ ϕ

/2, where it takes a value sin(ϕ

)/2π. Consequently, the modulus

(absolute value) of

χ can be written as



χ(r)



=−

2π

(sin

+cos

)

1/2

δ(r −r

−φ

/2)

2π

δ(r −r

−φ

/2)

(4.82)

and is proportional to the radial distribution function N

.IfEq.(4.77) is written

in terms of exp(ikr), or 2πikr as in Eq. (4.7), the RDF peaks occur at r = 2r

+ φ

and at r = 2r

/π +φ

/2π, respectively.

Including the Gaussian term of Eq. (3.167) is equivalent to convolving the trans-

form

χ with a function of the form exp



−r

/(2σ

)



. In other words, the effect of

thermal and (in a noncrystalline material) static disorder is to broaden each delta

function present in |

χ| into a Gaussian peak whose width is proportional to the cor-

responding disorder parameter σ

. To the extent that the inelastic mean free path λ

may be considered to be independent of k, the effect of the exponential term in Eq.

(3.167) is simply to attenuate the peaks in

χ, particularly at larger r

. Insofar as the

window approximates to a rectangular function, its effect will be to convolve each

Gaussian peak with a function

W of the form (Lee and Beni, 1977)

W =

sin(2k

max

−

sin(2k

min

(4.83)

Since k

max

is usually several times of k

min

, the ﬁrst of these sinc functions is

more important at small r, but both terms broaden the peaks in |

χ| and introduce

oscillations between the peaks.

In typical EXELFS studies (Johnson et al., 1981a; Leapman et al., 1981;

Stephens and Brown, 1981; Bourdillon et al., 1984), the widths of the

χ(r) peaks are

typically in the range of 0.02–0.1 nm (see Fig. 4.22), which i s considerably larger

than the thermal Debye–Waller broadening, at room temperature σ

<0.01nminthe

majority of materials (Stern et al., 1980). These peak widths, which determine the

accuracy with which the interatomic radii can be measured, are therefore a reﬂection

of the limited k-range. Fortunately, the sinc functions in Eq. (4.83) are symmetrical

(about r =0) and do not shift the maxima of |

χ(r)| and Im[χ(r)]. However, an error

in the choice of E

introduces a nonlinear term into Eq. (4.78), shifting the maxima

in |

χ(r)| and Im[χ(r)] by unequal amounts. This forms the basis of the scheme for

choosing E

by matching the peaks in these two functions (Lee and Beni, 1977).

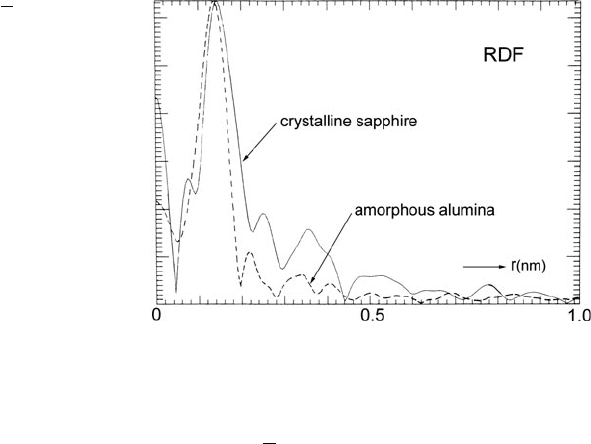
4.6 Analysis of Extended Energy-Loss Fine Structure 283

Fig. 4.22 χ (r) for crystalline

sapphire (solid curve)and

anodically deposited

amorphous alumina (broken

curve). The ﬁrst-shell radius

is 0.003 nm shorter in the

amorphous case, suggesting a

mixture of sixfold and

fourfold coordination. After

applying the phase shift

correction (Teo and Lee,

1979), all peaks are shifted by

0.049 nm to the right. (A. J.

Bourdillon, personal

communication.)

4.6.1.7 Correction for Phase Shifts

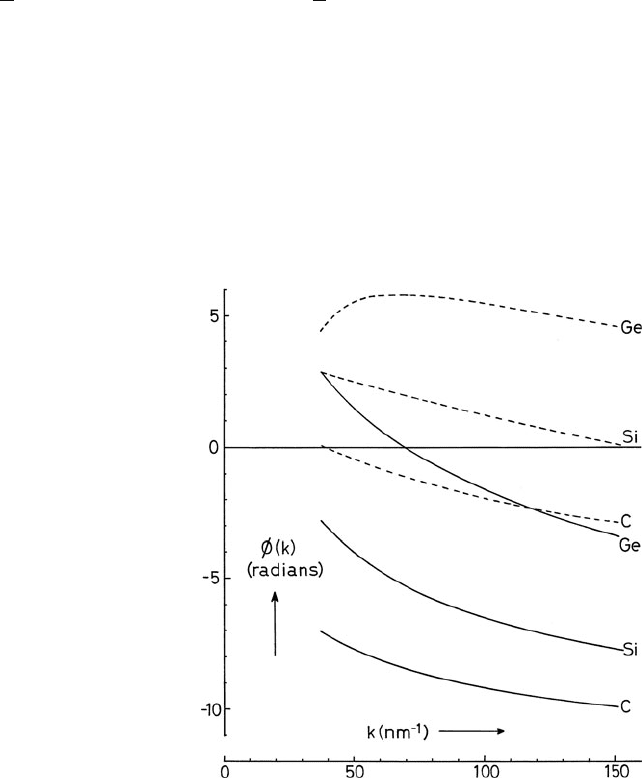
The ﬁnal step in the Fourier method is to estimate the linear (in k) component ϕ

of the phase shift in order to convert the χ(r) peak positions into interatomic dis-

tances. The phase function ϕ

(k) actually contains two contributions: a change ϕ

(k)

in phase as the ejected electron ﬁrst leaves and then returns to the emitting (and

“absorbing”) atom, and also a phase change ϕ

(k) that occurs upon backscattering

from a particular atomic shell. For K-shell EXELFS, where (as a result of the dipole

selection rule) the emitted wave has p-like character:

(k) = ϕ

(k) + ϕ

(k) − π (4.84)

The superscript on ϕ

(k) refers to the angular momentum quantum number l



of the

ﬁnal state (the emitted wave), while the ﬁnal term (−π)inEq.(4.84) accounts for a

factor (−1)

that should occur before the summation sign in Eq. (3.167), l referring

to the angular momentum of the initial state. In the case of EXELFS on an L

edge,

the emitted wave is expected to be mainly d-like (l



=2) and the phase term takes

the form (Teo and Lee, 1979)

(k) = ϕ

(k) + ϕ

(k) (4.85)

Note that ϕ

(k) depends on j and therefore on the atomic number of the backscatter-

ing atom, while ϕ

(k) depends on the atomic number of the emitting atom and on the

angular momentum quantum number l



of the emitted wave. The phase term ϕ

(k)

is therefore a property of two atoms (the emitting atom being speciﬁed) and of the

type of inner shell (K, L, etc.) giving rise to the EXELFS. It has been postulated that

(k) depends on the chemical environment, but experimental work suggests that

this is not the case (Citrin et al., 1976; Lee et al., 1981), at least for k >40nm

−1

.In

other words, “chemical transferability” of the phase shift can be applied, provided

the energy zero E

in Eq. (4.75) is chosen consistently.

284 4 Quantitative Analysis of Energy-Loss Data

Among others, Teo and Lee (1979) have therefore carried out ab initio calcu-

lations of ϕ

(k) and ϕ

(k) using atomic wavefunctions and have tabulated these

functions for certain values of k and atomic number. Data for intervening elements

can be obtained by interpolation. Ground-state wavefunctions were assumed for

most of the elements, which could lead to a systematic error in r

if the emitting

atom is strongly ionic (Stern, 1974; Teo and Lee, 1979). Some EXAFS workers

have calculated phase shifts using wavefunctions of the higher adjacent element

in the periodic table (the Z + 1 or “optical alchemy” approximation) to allow for

relaxation of the atom following inner-shell ionization (Section 3.8.5).

The value of ϕ

for use in Eq. (4.78) may be taken as the average slope of the

(k) curve in the region k

min

to k

max

(Leapman et al., 1981; Johnson et al., 1981a).

Since this average slope is negative (Fig. 4.23) and since r

= r − ϕ

/2 at the peak

χ(r)ther-value corresponding to each χ peak is increased by |ϕ

4.6.2 Curve-Fitting Procedure

Due to the width of the RDF peaks computed by Fourier transformation of χ(k), it

would be difﬁcult to accurately distinguish atomic shells that are separated by less

than 0.02 nm. An alternative procedure, employed successfully in EXAFS studies,

is to use Eq. (3.167) to calculate χ(k), starting from an assumed model of the atomic

Fig. 4.23 Phase shifts ϕ

(solid curves)andϕ

(broken

curves) as a function of

ejected electron wave

number, calculated by Teo

and Lee (1979)using

Herman–Skillman and

Clementi–Roetti

wavefunctions

4.6 Analysis of Extended Energy-Loss Fine Structure 285

structure, and then ﬁt this calculated function to the experimental data by varying

the parameters (f

, N

, σ

) of the model.

This approach has several advantages. More exact expressions can be used for

the phase function ϕ

(k), by including (for example) k

and k

−3

terms in Eq. (4.78)

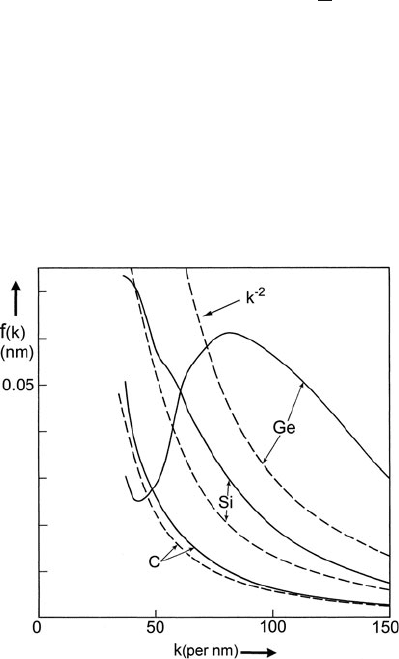
(Lee et al., 1977). The k-dependence of the backscattering amplitude f

(k) can be

taken into account more precisely, for example, by using a Lorentzian function (Teo

et al., 1977). This k-dependence can be different for different atomic shells and

departs signiﬁcantly from the k

−2

approximation in the case of medium- and high-

Z elements; see Fig. 4.24.Thek-dependence (energy-dependence) of the inelastic

mean free path λ

(Fig. 3.57) can also be included in the analysis. With this more

accurate t reatment, it has been possible in EXAFS investigations to estimate the

coordination number N

and disorder parameter σ

as well as interatomic distances.

Particularly in the case of a completely unknown structure, the Fourier transform

method (Section 4.6.1) may be used as a basis for selecting the initial parame-

ters of the atomic model. These parameters are then reﬁned by curve ﬁtting to the

experimental data, the process being an iterative one. Sometimes use is made of a

technique known as Fourier ﬁltering, in which the χ(k) modulation arising from a

single atomic shell is generated by back-transforming a small range of

χ(r), cor-

responding to a single peak in the RDF (Eisenberger et al., 1978); the parameters

of the model are then ﬁtted shell by shell, starting with the shell of smallest radius.

However, in many cases of practical interest the Debye–Waller and inelastic terms

in Eq. (3.167) damp the small-k oscillations (corresponding to large r

) to such an

extent that only nearest neighbor separations can be considered reliable.

A further advantage of the curve-ﬁtting procedure is that curvature of the emit-

ted wave (Pettifer and Cox, 1983) and multiple scattering of the ejected electron

(Lee and Pendry, 1975) can be taken into account. Equation (3.167) represents a

Fig. 4.24 Backscattering

amplitude f(k) from the

atomic calculations of Teo

and Lee (solid curves)and

from the Rutherford

scattering formula: Eq. (3.3)

with γ =1andq =2k.Note

that f(k) departs from the k

−2

dependence as the atomic

number of the element

increases

286 4 Quantitative Analysis of Energy-Loss Data

plane-wave approximation and tends to fail for higher order shells (i.e., at low k),

where backscattering takes place further away from the nucleus of the backscatter-

ing atom, which therefore “sees” a larger portion of the wave front. Equation (3.167)

also assumes only single (elastic) scattering of the ejected electron, a condition that

no longer applies to higher order shells. By removing these restrictions, EXAFS the-

ory has been extended to the near-edge (XANES) region (Durham et al., 1981, 1982;

Bianconi, 1983), forming a basis for analyzing energy-loss near-edge structure.

4.7 Simulation of Energy-Loss Near-Edge Structure (ELNES)

As outlined in Chapter 3, near-edge ﬁne structure can be calculated in real space

(multiple scattering procedure) or in reciprocal space (the band structure approach).

Advantages of the real-space method are that it can more easily deal with non-

crystalline situations, dopants or impurities, interfaces, and particles embedded in

a matrix for example. Advantages of the density functional approach are that the

same calculation can yield a large number of physical properties: band structure

diagrams, elastic constants, etc., as well as ELNES and low-loss spectra. The two

methods have been compared for the calculation of GaN, where it was concluded

that the density functional approach was somewhat more accurate but more time

consuming (Arslan et al., 2003; Moreno et al., 2006). Here we outline the properties

of some readily available software packages that perform each type of calculation.

4.7.1 Multiple Scattering Calculations

As described in Section 3.9,Eq.(3.167) retains validity within 50 eV of an ioniza-

tion threshold through the concept of an effective scattering amplitude that makes

allowance for multiple scattering, curvature of the emitted wavefront, inelastic scat-

tering, and core-hole effects. ELNES can therefore be simulated using an approach

similar t o EXELFS curve ﬁtting (Section 4.6.2).

These procedures are implemented in FEFF (Ankudinov et al., 1998), avail-

able from the University of Washington (http://leonardo.phys.washington.edu/feff).

Originally written for analysis of x-ray near-edge structure (XANES), this code has

been adapted to ELNES. The FEFF8 version is described within that context by

Moreno et al. (2007) and their review is largely applicable to FEFF9. The pro-

gram contains six modules. The ﬁrst calculates mufﬁn-tin potentials of the atoms

involved, using a self-consistent ﬁeld (SCF) method. The second evaluates phase

shifts, dipole matrix elements, and the local density of states (LDOS) in various

angular momentum projections. A third module carries out full multiple scattering

calculations for a speciﬁed cluster of atoms. The signiﬁcant multiple scattering paths

are then identiﬁed; effective scattering amplitudes are calculated for those paths and

the ELNES oscillations are computed.

4.7 Simulation of Energy-Loss Near-Edge Structure (ELNES) 287

The input ﬁle is divided into cards that specify conditions for the calculation.

FEFF9 introduces a graphical user interface to control the different cards, although it

can also be run in the same way as FEFF8. If a card is absent, default values are used.

However, an ATOMS card is essential since it speciﬁes the nature and coordinates

of the emitting atom and its neighbors, and is usually compiled using a separate

program through the WebAtoms interface (http://cars9.uchicago.edu/cgi-bin/atoms/

atoms.cgi). Unlike band structure methods, FEFF does not rely on atom periodity

or crystal symmetry, so defects s uch as vacancies, impurities, and interfaces can be

included in the atom cluster.

The program is typically run ﬁrst for a small cluster, containing ﬁrst- and

second-nearest neighbors, then the cluster size increased to see if the potentials

and ELNES oscillations have converged to a limit. Next, various calculated prop-

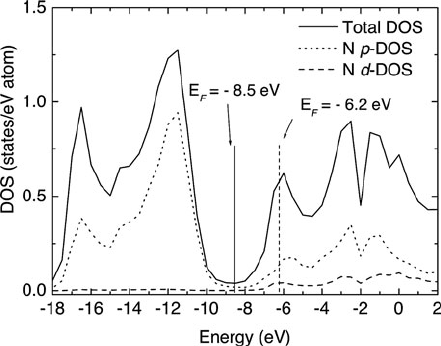
erties are checked, such as the densities of s tates and the Fermi level. In the GaN

example shown in Fig. 4.25, the Fermi level was found to initially lie above the

bandgap of the semiconductor. It was shifted downward by 1.7 eV to mid-gap

position using the EXCHANGE card, which also allows a choice of the electron

self-energy (either Hedin–Lundqvist or Dirac–Hara exchange correlation poten-

tial), whose imaginary part determines the inelastic mean free path of the ejected

electron. The COREHOLE card allows a choice between inclusion of a core hole

(recommended for nonmetallic systems) and its absence due to free-electron screen-

ing (appropriate for metals). In general, the effect of a core hole is to redshift the

edge to lower energy and sharpen the rise at the threshold, as in Fig. 4.26c.

The ELNES calculations include core-hole initial-state broadening (from tables)

and ﬁnal-state broadening (from imaginary part of the calculated self-energy)

but instrumental broadening can also be introduced, through the EXCHANGE or

CORRECTIONS card. For hexagonal GaN, inclusion of eight atom shells repro-

duced all four peaks visible above the nitrogen K-edge but 142 shells (480 atoms)

Fig. 4.25 Total density of

states for hexagonal GaN,

together with p and d partial

densities of states for a

nitrogen atom, calculated by

FEFF8. The initial and ﬁnal

positions of the Fermi level

are indicated by vertical lines.

From Moreno et al. (2007),