Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

248 4 Quantitative Analysis of Energy-Loss Data

4.2.4 Correction for Surface Losses

Equations (4.26), (4.27), and (4.28) assume that energy losses take place only within

the interior of the specimen. If the specimen thickness is below about 50 nm,

it is desirable to make allowance for surface losses. For perpendicular incidence,

Eq. (3.80) gives the single-scattering surface-loss intensity from both surfaces (but

neglecting coupling between them) as

(

)

= 2I

πa



tan

−1

(

β/θ

)

−

(β

+θ

)



4ε

(

)

+ε

−Im



−1





(4.31)

where T = m

/2 and the β/(β

+ θ

) term is usually negligible. For a clean

surface, ε

= 1. For a metal specimen whose surfaces are covered by an oxide of

permittivity ε

, i t may be better to r eplace ε

+ 1byε

+ ε

in Eq. ( 4.31). If the

frequency dependence of ε

is known, Eq. (4.31) could incorporate the energy-loss

function given in Eq. (3.80).

After subtracting the estimated S

(E) from the experimental single-scattering dis-

tribution J

(E), a new normalization constant K is found and ε(E) is recalculated.

The whole process is repeated if necessary until the result converges (Wehenkel,

1975). After this procedure, the value of ε

at small E(≈ 2 eV) should approximate

to the optical value used in applying Eq. (4.27).

Whether the iteration converges depends largely on the form of the loss spec-

trum at low energies (<10 eV). The surface-loss correction above is valid only for a

smooth and planar surface, perpendicular to the incident beam, and ignores retarda-

tion effects. A favorable case is a deconvolved spectrum of a thicker metal ﬁlm,

where surface losses are weak and

Cerenkov losses absent. For semiconductors

and insulators, Stöger-Pollach et al. (2008) propose taking the difference between

the original spectrum and that calculated from the Kröger formula and subtracting

this difference during the iteration. Further details are discussed in Stöger-Pollach

(2008). It is also necessary to deal with the singularity in Eq. (4.31)atE =0, as

discussed in Section B.9.

4.2.5 Checks on the Data

The Bethe f-sum rule (Section 3.2.4) gives rise to the concept of an effective number

of electrons contributing to energy losses up to a value E.FromEq.(3.35), one

deﬁnition of the effective number of electrons per atom (or per molecule) is

eff



−Im ε

−1



2ε

π







−1





(4.32)

4.3 Deconvolution of Core-Loss Data 249

where n

is the number of atoms (or molecules) per unit volume of the sample.

Alternatively, Eq. (3.34) can be applied to optical transitions (q ≈ 0), leading to a

second effective number:

eff

(

)



(

0, E

)

dE =

2ε

π





(4.33)

Because of the 1/E weighting factor in the relationship between dσ/dE and df /dE,

eff

(−Im ε

−1

) remains less than n

eff

(ε

) at low values of E but the two numbers

converge toward the same value at higher energy loss; see Fig. 4.4d. In favor-

able cases (elements and simple compounds), this plateau corresponds to a known

number of electrons per atom, providing a check on the derived values of ε

(E)

and Im[−1/ε(E)]. In elemental carbon, for example, n

eff

≈ 4, corresponding to

excitation of all the valence electrons, for energies (≈ 200 eV) approaching the

K-ionization t hreshold (Hagemann et al., 1974); see Fig. 5.8. In compounds con-

taining several elements, inner-shell excitation can occur before the valence electron

contribution is exhausted, so plateau values are never reached and it is possible to

tell if the derived values of n

eff

are substantially too high but not whether they are

too low. This difﬁculty is removed if the analysis can be carried out up to an energy

loss several times the largest inner-shell binding energy of the elements involved;

the ﬁnal saturation value should then correspond to the total number of electrons per

atom (or molecule).

4.3 Deconvolution of Core-Loss Data

As noted in Section 3.7.3, plural scattering can drastically alter the observed shape

of an inner-shell ionization edge and may need to be removed before near-edge or

extended ﬁne structure can be interpreted. This plural scattering involves electrons

that undergo one or more low-loss collisions (e.g., plasmon excitation) in addition

to causing core-level ionization. The probability of more than one core ionization

can be neglected in transmission spectroscopy, where the sample thickness is small

compared to the inner-shell mean free path. Because the core-loss region typically

contains many data points, equally spaced in energy, fast-Fourier methods are a

natural choice for spectral processing.

4.3.1 Fourier Log Method

The deconvolution method of Johnson and Spence (1974), described in

Section 4.1.1, assumes only that scattering events are independent, and that the prob-

ability of plural scattering is given by Poisson statistics. This method is therefore

250 4 Quantitative Analysis of Energy-Loss Data

capable of removing plural scattering from anywhere within the energy-loss spec-

trum, including the mixed (core + plasmon) scattering beyond an ionization edge. It

involves calculating a Fourier transform of the entire spectrum, from the zero-loss

peak up to and beyond the ionization edge(s) of interest. To prevent truncation errors

from affecting the SSD within the range of interest, the spectrum must be recorded

up to an energy loss well beyond these edges or else extrapolated smoothly toward

zero intensity at some high energy loss.

Any discontinuities in the spectrum must be removed before calculating its trans-

form. For example, low-loss and core-loss regions obtained by separate readouts

from a parallel recording spectrometer must be “spliced” together. The resulting

spectrum will often have a large dynamic range (e.g., 10

) but Fourier proce-

dures usually provide the necessary precision, using the procedures described in

Section 4.1.1.

Unlike the Fourier ratio method described in Section 4.3.2, Fourier log deconvo-

lution removes plural scattering from both the core-loss region and the preceding

background. Because the core-loss intensity just above the ionization threshold

arises only from single inner-shell scattering, the “jump ratio” of an edge increases

after Fourier l og processing, the increase being dramatic in the case of moderately

thick samples; see Fig. 4.6. In this respect, the deconvolved spectra are equivalent

to those that would be obtained using a thinner sample or a higher incident energy.

However, the noise components arising from the plural scattering remain behind

after deconvolution, so statistical errors of background subtraction (Section 4.4.4)

remain much the same. Therefore Fourier log deconvolution improves the sensi-

tivity and accuracy of elemental analysis only to the extent that systematic errors in

background ﬁtting may be reduced, for example, if the single-scattering background

approximates more closely to a power-law energy dependence (Leapman and Swyt,

1981a).

In addition to increasing the fractional noise content of the pre-edge background,

Fourier log deconvolution tends to accentuate any artifacts present in the spectrum,

e.g., due to power supply ﬂuctuations or nonlinearity in the intensity scale. An exam-

ple is shown in Fig. 4.6, where splicing of the low-loss spectrum to the core-loss

region resulted in a change in slope. Deconvolution converts this change in slope

into a “hump” extending over tens of eV, which might be mistaken for an ionization

edge. Although somewhat extreme, this example illustrates the need for high-quality

data prior to deconvolution.

4.3.2 Fourier Ratio Method

This alternative Fourier technique involves two regions of the spectrum. One of

them, usually the low-loss region J

(E) containing the zero-loss peak and energy

losses up to typically 100 eV, is used as a deconvolution function or “instrument

function” for the second region. The latter is typically the background-subtracted

core-loss region J

(E), in which case the result should be an unbroadened single-

scattering core-loss intensity K

(E), obtained on the assumption that

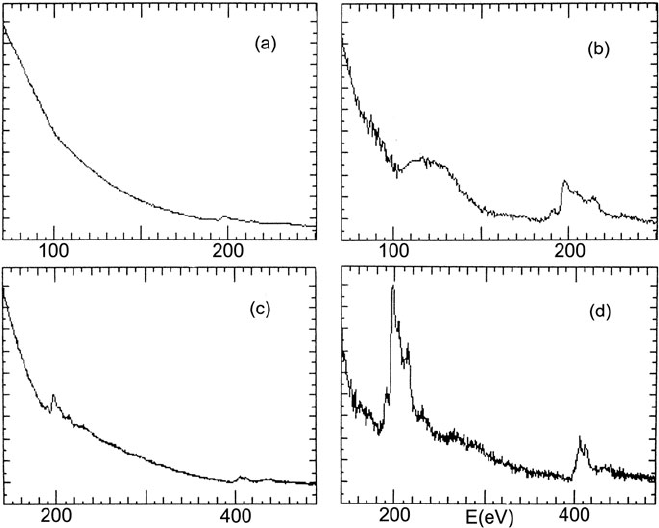
4.3 Deconvolution of Core-Loss Data 251

Fig. 4.6 (a) Part of the energy-loss spectrum recorded from a thick region of a boron nitride

(t/λ =1.2) using 80-keV incident electrons and β =100 mrad. (b) Same energy region after Fourier

log deconvolution, showing an artifact generated from the change in slope at 100 eV (the position of

the original gain change). (c) Extended energy range, showing the boron and nitrogen K-ionization

edges prior to deconvolution. (d) Boron and nitrogen K-edges after Fourier log deconvolution.

From Egerton et al. (1985), with permission of the Royal Society

(E) = K

(E)

∗

(

)

(4.36)

Instrumental broadening is present on both sides of this equation, in the functions

(E) and J

(E) but not in K

(E). The rationale behind this assumption is that plas-

mon scattering contributes to the core-loss integral in the same proportion as it

contributes to intensity in the low-loss region (including the zero-loss peak), i.e.,

= I

; see Fig. 4.7. Plasmon/core-loss coupling is assumed negligible

(Egerton, 1976b).

Taking Fourier transforms of both sides of Eq. (4.36)givesj

(v) = k

(v)j

(v)/I

which is inverted to give

(v) = I

(v)/j

(v)] (4.37)

Equation (4.37) shows that, in principle, the measured core-loss intensity J

(E)

can be corrected for both plural scattering and instrumental broadening by taking

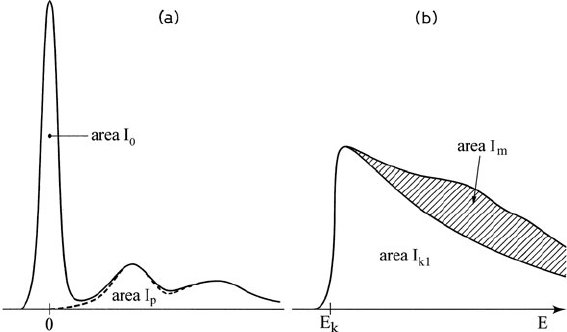
252 4 Quantitative Analysis of Energy-Loss Data

Fig. 4.7 (a) Low-loss region of an energy-loss spectrum. (b) Background-subtracted ionization

edge, whose integral I

is increased by an amount I

due to mixed (core + plasmon) scattering

a ratio of two Fourier transforms and multiplying by the zero-loss integral I

.As

with the Fourier log method, however, such “complete” deconvolution is problem-

atic because high-frequency noise components present in j

(v) become “ampliﬁed”

when divided by j

(v). As in Section 4.1.1, this noise ampliﬁcation can be avoided

in several ways:

(a) Gaussian modiﬁer. Multiplying the ratio of Fourier coefﬁcients by a Gaussian

function exp(−π

)gives

(v) = I

exp(−π

)[j

(v)/j

(v)] (4.38)

If σ = E/1.665, where E is the FWHM of the zero-loss peak, the inverse

transform of j

(v) will be a core-loss SSD whose energy resolution and noise

content are very similar to those of the original data. If the zero-loss peak in

(E) occurs at data channel m = m

, the inverse transform J

(E) is shifted to

the l eft of m

channels, relative to J

(E).

(b) Zero-loss modiﬁer. Using the zero-loss peak Z(E) as the noise-limiting modiﬁ-

cation function gives

(v) = z(v)[j

(v)/j

(v)] (4.39)

Assuming the energy resolution E to be independent of energy loss, the

inverse transform J

(E) will have an energy resolution identical to that of J

(E).

If Z(E) peaks at the same channel as the zero-loss peak present in J

(E), the

energy shift associated with method (a) is avoided, but three Fourier transforms

must be calculated rather than two.

(E) and its associated

noise N(E) are known approximately, it is possible to choose a noise-rejection

4.3 Deconvolution of Core-Loss Data 253

function g(v) that provides a good compromise between noise and resolution

in the single-scattering distribution. The aim is to perform deconvolution only

for frequencies where the signal/noise ratio is > 1. A function with a sharp

cutoff at v = v

must be avoided, since it would introduce convolution with

sin(2πv

E)/(2π v

E), resulting in oscillatory artifacts adjacent to any sharp fea-

tures in the SSD. A modest increase of energy resolution is possible by using a

Wiener ﬁlter function of the form

g(v) =

(v)

{

(v)

+1/SNR}

−1

(4.40)

where SNR is an estimated signal/noise ratio in the core-loss region.

(d) Delta function approximation. If we ignore instrumental broadening of the

inelastic data, taking the low-loss spectrum to be J

(E), in which the zero-loss

peak Z(E) replaced by a delta function of equal area,

(E) ≈ J

(E)

∗

(

)

(4.41)

so that

(v) ≈ I

(v)/j

(v) (4.42)

Because the delta function present in J

(E) contains high-frequency Fourier

components, noise ampliﬁcation is avoided. The procedure gives good results

provided the core-loss data J

(E) contains no sharp peaks of width comparable

to the instrumental resolution.

4.3.2.1 Practical Details

Before applying Fourier ratio deconvolution as described above, the low-loss and

core-loss data must be present in computer memory arrays containing the same num-

ber N of channels; for the FFT algorithm, N = 2

where k is an integer. These two

spectra can be from separate acquisitions, with different integration times or incident

beam intensities, but must have the same electron volt/channel. The background to

the lowest energy ionization edge is ﬁrst removed, as described in Section 4.4, and

the intensity extrapolated to zero at the high-E end of the range. This procedure

makes the intensity the same at both ends of the array and satisﬁes the continuity

requirement for a Fourier series; see Section 4.1.1. Likewise, the intensity should be

approximately zero at both ends of the low-loss spectrum.

If necessary, complex numbers can be avoided by computing real and imagi-

nary Fourier coefﬁcients (see Section 4.1.1 and Appendix B) and processing them

according to the rules of complex division. For example,

(v)

+ij

−j

(4.43)

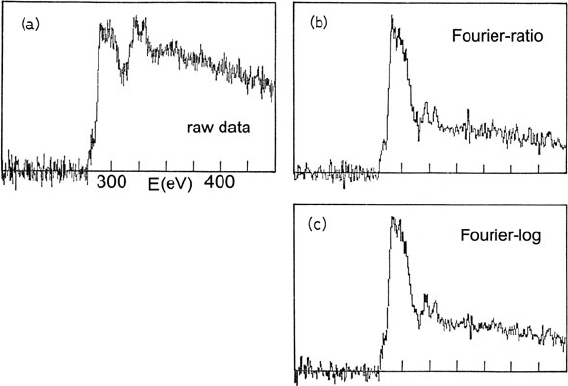
254 4 Quantitative Analysis of Energy-Loss Data

Fig. 4.8 (a) Carbon K-edge recorded from a thick sample of graphite using 80-keV incident elec-

trons and a collection semi-angle β ≈ 100 mrad. (b) Single-scattering K-loss intensity recovered

using the Fourier ratio method. (c) Single-scattering distribution obtained by Fourier log decon-

volution, followed by background subtraction. From Egerton et al. (1985), with permission of the

Royal Society

In the case of noise-free data and a specimen of uniform thickness, the Fourier

ratio method can be shown to be equivalent to Fourier log deconvolution (Swyt and

Leapman, 1984). Applied to real data, the two methods give results which are very

similar; see Fig. 4.8.

4.3.2.2 Effect of a Collection Aperture

If F

, F

, and F

are fractions of the plasmon-loss, core-loss, and double (core-

loss + one-plasmon) scattering that pass through an angle-limiting collection

aperture, the fraction of double scattering remaining after Fourier log deconvolution

can be shown to be

= (F

−F

)/F

(4.44)

which is analogous to Eq. (4.25) and applies to both Fourier log and Fourier ratio

deconvolution.

The angular distribution of double scattering can be calculated as an angular

convolution of the core-loss and plasmon angular distributions. Taking the latter to

be a Lorentzian function with a cutoff at θ

, R

is estimated to be less than 4% for

β>θ

(Egerton and Wang, 1990). The plural scattering intensity left behind after

deconvolution is appreciable only for small values of β and high-energy edges; see

Fig. 4.9.

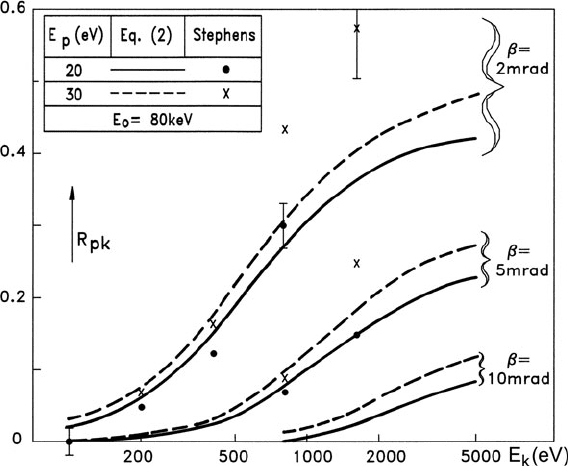
4.3 Deconvolution of Core-Loss Data 255

Fig. 4.9 Fraction of mixed (plasmon + core-loss) scattering remaining after deconvolution, plotted

against edge energy for plasmon energies of 20 and 30 eV and three values of collection semi-

angle. The calculations are for an incident energy of 80 keV, allowing direct comparison with the

data points based on Monte Carlo simulations of Stephens (1980). From Egerton and Wang (1990),

4.3.3 Bayesian Deconvolution

Maximum-entropy and maximum-likelihood deconvolution (Section 4.1.3) can be

applied to the core-loss region, taking the kernel as either the zero-loss peak or the

entire low-loss region (extrapolated to zero at the highest energy loss, if necessary).

In the latter case, deconvolution removes plural (core + plasmon) scattering from the

ionization edge, as well as sharpening it. Figure 4.10(a,b) illustrates how Bayesian

deconvolution can improve the energy resolution and dramatically increase the split-

ting of overlapping peaks, provided the spectral intensity (counts per channel) is

high and the shot noise correspondingly low. Using the Richardson-Lucy algorithm,

Gloter et al. (2003) reported an increase in resolution from 0.9 eV to 0.3 eV at

the diamond K-edge. Kimoto et al. (2003) applied the same algorithm to the boron

K-edge in BN, sharpening the π

∗

-peak from 0.52 to 0.35 eV (FWHM).

One advantage of these methods is their response to discontinuities in the data;

as shown in Fig. 4.10c, artifacts are generated locally rather than spread across the

spectrum, as with Fourier methods. In fact, raw core-loss data (without background

subtraction or extrapolation) can be processed without generating obvious artifacts

simply by choosing the energy range so that the spectral intensity is equal at both

ends (Egerton et al., 2008).

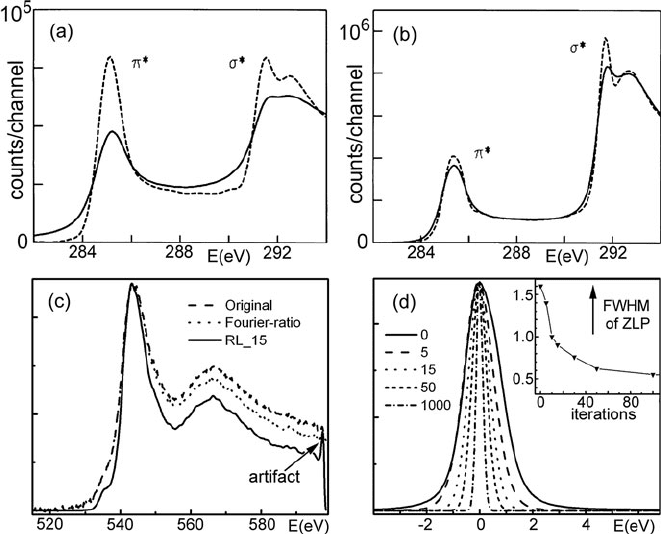
256 4 Quantitative Analysis of Energy-Loss Data

Fig. 4.10 Carbon K-edge if graphite before (solid curve)andafter(dashed curve)maximum

entropy deconvolution. The spectra were recorded with an energy resolution of (a) 0.9 eV and

(b) 0.4 eV; in both cases deconvolution enhances the splitting of the σ

∗

peak. From Overwijk and

Reefman (2000), copyright Elsevier. (c) Oxygen K-edge after Fourier ratio deconvolution (dotted)

and Richardson–Lucy deconvolution and sharpening (solid curve) with 15 iterations. The arrow

shows an artifact generated by the discontinuity in intensity at 510 and 600 eV. (d) Peak generated

by using a low-loss spectrum of Si

as both the data and the kernel in RL deconvolution. From

Since core-loss data do not contain a zero-loss peak, there is no immediate way of

judging the energy resolution after a given number of iterations. However, by using

the same (zero-loss or low-loss) data as both data and kernel, a peak is generated

(at E =0) whose width gives an approximate indication of the resolution after a

given number of iterations; see Fig. 4.10d.

4.3.4 Other Methods

Muto et al. (2006a) describe use of the Pixon method, based on Bayes’ theorem but

said to avoid the global oversmoothing inherent in the maximum entropy method. It

was applied to the two-dimensional output of the CCD camera of the Enﬁna spec-

trometer, thereby correcting for the detector point-spread function and for curvature

4.4 Separation of Spectral Components 257

of the spectrum in the cross-dispersion direction. The authors demonstrate that a

LaB

source run at low current can achieve an energy resolution of 0.6 eV at

the K-edge π

∗

peak of h-BN, becoming 0.38 eV after deconvolution. Muto et al.

(2006b) demonstrate that the Pixon method can deal with noisy core-loss data.

Wachtmeister and Csillag (2011) describe an iterative method (Gold, 1964)for

increasing the energy resolution, based on matrix manuiplation. By using the low-

loss spectrum as a response function, plural scattering was simultaneously removed

from core-loss data, giving results in agreement with Fourier ratio deconvolution.

A method for removing plural scattering has been described, based on spectra

recorded from samples of different thickness (Bradley et al., 1985) or different inci-

dent beam energy (Gibbons et al., 1987). It uses a delta function approximation for

the zero-loss peak, so no attempt is made to sharpen the data, and incorporates an

expression for the angular dependence of scattering, so the method can accommo-

date spectra recorded with an off-axis collection aperture (Bradley and Gibbons,

1986). Reasonable results were obtained from aluminum K-edge data.

Verbeeck and Bertoni (2009) reported results on a model-based procedure that

used maximum entropy or maximum-likelihood ﬁtting of simulated core-loss data

to the expression O(E)

∗

P(E) + B(E). Here P(E) is a low-loss function that includes

instrumental broadening and plural scattering, O(E) represents a parameterized

model of the core-loss SSD and B(E) is a parameterized background. O(E)was

taken to be a product of a smooth atomic edge proﬁle σ (E) and an “equalization”

function f(E) representing ELNES modulations. The number of variable parame-

ters was chosen as a compromise between the accuracy of the model (including

energy resolution) and error bars of the parameters themselves. For the simulated

data, f(E) was calculated using the FEFF program (Section 4.7), P(E) being a set

of Poisson-weighted Lorentzian functions representing the low-loss spectrum, with

B(E) a power-law background. Poisson noise was added to O(E) and P(E)tosim-

ulate real data. The degree of ﬁt was measured from the RMS deviation between

the ﬁtted O(E) and the known true value, for comparison with the RMS devia-

tion obtained from Fourier deconvolution with a Gaussian modiﬁer or Wiener ﬁlter.

Differences between the methods were modest (less than a factor of 2) but RMS val-

ues were smallest for the model-based procedure. An assumption of this procedure

is that the spectral components involved are known and can be reliably simulated.

4.4 Separation of Spectral Components

An energy-loss spectrum contains contributions from various types of inelastic

scattering, and it is often necessary to separate these components for subsequent

study. The most common requirement is separation of an ionization edge from its

underlying background, for the purpose of elemental or ﬁne structure analysis. In

this Section, we begin by discussing methods for modeling and extrapolating this

background, together with the statistical and systematic errors involved. We then

consider more elaborate methods that are used to identify and separate spectral

components in a more general way.