Egerton R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope

Подождите немного. Документ загружается.

228 3 Physics of Electron Scattering

scattering, the elastic contrast should diminish as the specimen thickness becomes

very small, unlike other forms of dark-ﬁeld contrast.

One further aspect of delocalization is the extent to which core-loss ﬁne structure

changes with position in the specimen. This structure can be regarded as aris-

ing from interference with electron waves backscattered from neighboring atoms

(Section 3.8.2). Multiple scattering calculations indicate that backscattering is sig-

niﬁcant within a diameter of 1–2 nm but that contributions from more distant atomic

shells have almost random phase and contribute little to the interference, so the ﬁne-

structure oscillations can change on a sub-nanometer scale (Wang et al., 2008a).

ELNES measurements across a sharp grain boundary appear to conﬁrm this predic-

tion; see Fig. 3.63. This delocalization can be regarded as a separate limit to the

spatial resolution of ELNES data and might be added in quadrature to the value

given by Eq. ( 5.17), for example (Wang et al. 2008a).

Another example is shown in Fig. 3.64, where the measured and calculated ﬁne

structure appears quite dissimilar at differently bonded carbon atoms, located within

a layer of graphene and at its edge (Suenaga and Koshino, 2010). These results

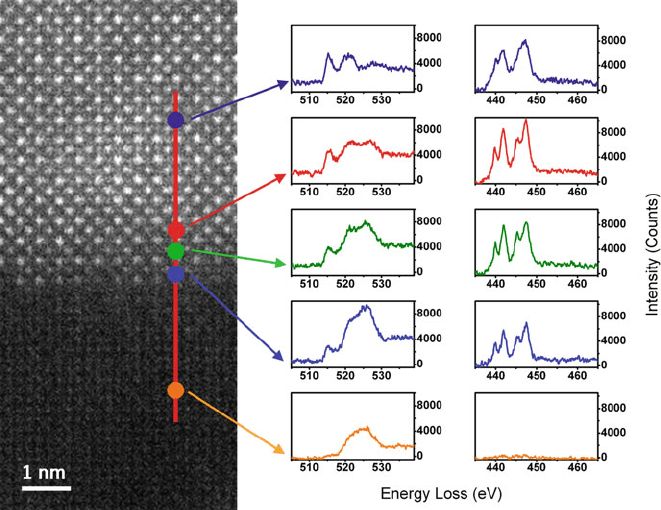
Fig. 3.63 Fine structure at the oxygen K- and titanium L

edges, measured at locations close

to a boundary between Ba

0.4

0.6

0.5

and MgAl

(horizontal in the 4.5 nm × 10 nm

HAADF image) and showing a transition between Ti

and Ti

valency. From Shao et al. (2011),

3.11 Delocalization of Inelastic Scattering 229

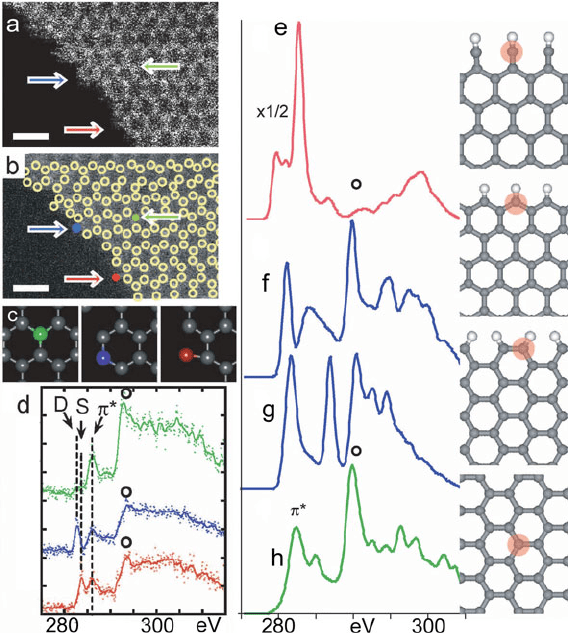
Fig. 3.64 (a) ADF image of a single-graphene layer at the edge of a HOPG ﬂake, recorded using

a 60-kV STEM ﬁtted with DELTA corrector. The scale bar represents 0.5 nm. (b)Sameimage

with each C atom outlined with a bright circle and three selected atoms (green, blue,andred)

arrowed. (c) Graphene-sheet model with single-, double-, and triple-bonded atoms identiﬁed. (d)

K-edges recorded (in <1 s with 40-mrad collection angle) from the green, blue,andred atoms.

(e–h) Near-edge structure calculated using DFT theory for a (e) single-bonded atom at a Klein

edge, (f) double-bonded atom at a zigzag edge, (g) double-bonded atom at an armchair edge, and

(h) triple-bonded atom away from the edge, each kind of atom being identiﬁed by a pink circle

on the right. The symbol o represents a n excitonic peak. Reproduced from Suenaga and Koshino

(2010), copyright Nature Publishing

indicate that core-loss ﬁne structure may be very localized in some structures, allow-

ing bonding information to be obtained from a single atom if radiation damage

permits. In this case, the STEM was operated at 60 kV, below the threshold for

displacement damage in graphene (for atoms located away from an edge).

Chapter 4

Quantitative Analysis of Energy-Loss Data

This chapter discusses some of the mathematical procedures used to extract

quantitative information about the crystallographic structure and chemical compo-

sition of a TEM specimen. Although this information is expressed rather directly

in the energy-loss spectrum, plural scattering complicates the data recorded from

specimens of typical thickness. Therefore it is often necessary to remove the effects

of plural scattering from the spectrum or at least make allowance for them in the

analysis procedure.

We start with the low-loss region, which might be deﬁned as energy losses

below 50 or 100 eV. Within this region, the main energy-loss mechanism involves

excitation of outer shell electrons: the valence electrons or (in a metal) conduc-

tion electrons. In many solids, a plasmon model (Section 3.3.1) provides the best

description of valence electron excitation, a process that occurs with relatively high

probability because the plasmon mean free path is often comparable with the sample

thickness.

4.1 Deconvolution of Low-Loss Spectra

Deconvolution techniques based on the Fourier transform will be described ﬁrst,

since they are widely used. Alternative methods that are applicable to the low-loss

region are outlined in Sections 4.1.2 and 4.1.3.

4.1.1 Fourier Log Method

Assuming independent scattering events, the electron intensity I

, integrated over

energy loss and corresponding to inelastic scattering of order n, follows a Poisson

distribution:

= IP

= (I/n!)(t/λ)

exp(−t/λ) (4.1)

231

R.F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope,

DOI 10.1007/978-1-4419-9583-4_4,



Springer Science+Business Media, LLC 2011

232 4 Quantitative Analysis of Energy-Loss Data

where I is the total integrated intensity (summed over all n), P

is the probability of

n scattering events within the specimen (thickness t), ! denotes a factorial, and λ is

the mean free path for inelastic scattering.

The case n =0 corresponds to the absence of inelastic scattering and is repre-

sented in the energy-loss spectrum by the zero-loss peak:

Z(E) = I

R(E) (4.2)

where the resolution or instrument response function R(E) has unit area and a full

width at half maximum (FWHM) equal to the instrumental energy resolution E.

Single scattering corresponds to n =1 and is characterized by an intensity

distribution S(E). From Eq. (4.1)

∞



S(E) dE = I

= I(t/λ)exp(−t/λ) = I

(t/λ) (4.3)

Owing to the limited instrumental resolution, single scattering occurs within the

experimental spectrum J(E) as a broadened distribution J

(E) given by

(E) = R(E)

∗

S(E) ≡

∞



−∞

R(E − E



)S(E



)dE



(4.4)

where

∗

denotes a convolution over energy loss, as deﬁned by Eq. (4.4).

Double scattering has an energy dependence of the form S(E)

∗

S(E). However,

the integral of this self-convolution function is (I

)

= (I

t/λ)

, whereas

Eq. (4.1) indicates that the integral I

should be I

(t/λ)

/2!. Measured using an

ideal spectrometer system, the double-scattering component would therefore be

D(E) = S(E)

∗

S(E)/(2!I

), but as recorded by the instrument, it is

(E) = R(E)

∗

D(E) = R(E)

∗

S(E)

∗

S(E)/(2!I

) (4.5)

Likewise, the triple-scattering contribution is equal to T(E) = S(E)

∗

S(E)

∗

S(E)/(3!I

), but is recorded as J

(E) = R(E)

∗

T(E).

The recorded spectrum, including the zero-loss peak, can therefore be written in

the form

Here λ characterizes all inelastic scattering in the energy range over which the intensity is inte-

grated, and is given by Eq. (3.96) in the case where several inelastic processes contribute within

this range. As discussed i n Section 3.4, Poisson statistics still apply to a spectrum recorded with an

angle-limiting aperture, provided an aperture-dependent mean free path is used.

4.1 Deconvolution of Low-Loss Spectra 233

J(E)=Z(E) + J

(E) + J

(E) +···

= R(E)

∗

δ(E) +S(E) +D(E) +T(E) +···]

= Z(E)

∗

[δ(E) +S(E)/I

+S(E)

∗

S(E)/(2!I

)

+ S(E)

∗

S(E)

∗

S(E)/(3!I

) +···]

(4.6)

where δ(E) is a unit area delta function.

The Fourier transform of J(E) can be deﬁned (Bracewell, 1978; Brigham,

1974)as

j(v) =

∞



−∞

J(E)exp(2π ivE) dE (4.7)

Taking transforms of both sides of Eq. (4.6), the convolutions become products

(Bracewell, 1978), giving the equation

j(v) = z(v){1 + s(v)/I

+[s(v)]

/(2!I

) +[s(v)]

/(3!I

) +···}

= z(v)exp[s(v)/I

]

(4.8)

in which the Fourier transform of each term in Eq. (4.6) is represented by the equiv-

alent lower case symbol, and is a function of the transform variable (or “frequency”)

v whose units are eV

−1

. Equation (4.8) can be “inverted” by taking the logarithm of

both sides (Johnson and Spence, 1974), giving

s(v) = I

ln[j(v)/z(v)] (4.9)

4.1.1.1 Noise Problems

One might envisage taking the inverse Fourier transform of Eq. (4.9) in order to

recover an “ideal” single-scattering distribution, unbroadened by instrumental res-

olution. However, as discussed by Johnson and Spence (1974) and by Egerton and

Crozier (1988), such “complete” deconvolution is feasible only if the spectrum

is coarsely sampled or noise free. In practice, J(E) contains noise (due to count-

ing statistics, for example) that extends to high frequencies, corresponding to large

values of v. Although not necessarily a monotonic function of v, the noise-free com-

ponent of j(v) eventually falls toward zero as v increases. As a result, the fractional

noise content in j(v) increases with v, and at high “frequencies” j(v) is dominated

by noise. Because z(v) also falls with increasing v, the high-frequency noise content

of j(v) is preferentially “ampliﬁed” when divided by z(v), as in Eq. (4.9), and the

inverse transform S(E) is submerged by high-frequency noise. Essentially, Eq. (4.9)

fails because we are attempting to simulate the effect of a spectrometer system

with perfect energy resolution and to recover ﬁne structure in J(E) that is below

the resolution limit.

Fortunately, deconvolution based on Eq. (4.9) can be made to work if we are

content to recover the instrumentally broadened single-scattering distribution J

(E),

234 4 Quantitative Analysis of Energy-Loss Data

with little or no attempt to improve the energy resolution. Several slightly different

procedures have been employed to obtain J

(E):

(a) Gaussian modiﬁer.IfEq.(4.9) is multiplied by a function g(v) that has

unit area and falls rapidly with increasing v, the high-frequency values of

ln(j/z) are attenuated and noise ampliﬁcation is controlled. The inverse trans-

form then corresponds to G(E)

∗

S(E), the single-scattering distribution recorded

with an instrument whose resolution function is G(E), known as a modiﬁca-

tion or reconvolution function. A sensible choice is the unit area Gaussian:

G(E) =(σ

√

π)

−1

exp(−E

/σ

) whose FWHM is W = 2σ

√

(ln 2) = 1.665σ,

in which case the single-scattering distribution (SSD) is obtained as the inverse

transform of

(v) = g(v)s(v) = I

exp(−π

)ln[j(v)/z(v)] (4.10)

A limited improvement in energy resolution is possible by choosing σ such

that W <E, but at the expense of increased noise content. If σ is cho-

sensothatW = E, the inverse transform J

(E) is the SSD that would

be recorded using an instrument having the same energy resolution E but

with a symmetric (Gaussian) resolution function. Besides removing plural

scattering from t he measured data, procedure (a) therefore corrects for any

distortion of peak shapes caused by a skew or irregularly shaped instrument

function.

(b) Zero-loss modiﬁer.IfG(E) = R(E), Eq. (4.10) becomes

(v) = r(v)s(v) = z(v)ln[j(v)/z(v)] (4.11)

Taking the inverse transform gives the single-scattering distribution J

(E) that

would be recorded from a vanishingly thin specimen. In Eq. (4.11)weare

using the zero-loss peak as the modiﬁcation function and the easiest way of

obtaining Z(E) is from the experimental spectrum J(E), setting channel con-

tents to zero above the zero-loss peak. For thicker specimens, it may be more

accurate to record Z(E) in a second acquisition with no specimen present;

difference in height between the two zero-loss peaks can be shown to result

in artifacts that are conﬁned to the zero-loss region (Johnson and Spence,

1974).

within the logarithm of Eq. (4.11) by a Gaussian function of the same width

and area, j

(v) can be obtained from the equation

(v) = I

exp(−π

){ln[j(v)] −ln[I

] +π

} (4.12)

4.1 Deconvolution of Low-Loss Spectra 235

where σ =E/1.665. This procedure avoids the need to isolate or remeasure

Z(E) and calculate its Fourier transform but can generate artifacts if Z(E)isnot

close t o Gaussian.

(d) Replacement of Z(E) by a delta function. If the zero-loss peak Z(E) in the orig-

inal spectrum is replaced by I

δ(E) before calculating the transform j

(v), one

can use the approximation (Leapman and Swyt, 1981a):

(v) ≈ I

ln[j

(v)/I

] (4.13)

As in (c), only one forward and one inverse transforms are needed and noise

ampliﬁcation is avoided. However, the use of Eq. (4.13) is equivalent to treating

the experimental spectrum as if it had been recorded using a spectrometer sys-

tem with perfect energy resolution and the resulting SSD will differ somewhat

from that derived using Eq. (4.11)ifJ(E) contains sharp peaks, comparable in

width t o the instrumental resolution (Egerton et al., 1985).

4.1.1.2 Practical Details

The Fourier transforms j(v) and z(v) are (in general) complex numbers of the form

+ij

and z

+iz

, where i = (−1)

1/2

. Therefore we have

j(v)

z(v)

+i(j

−j

)

(4.14)

ln[j(v)/z(v)] = ln r +iθ (4.15)

where

r =



(

)

+(j

−j

)



1/2

(4.16)

and

θ = tan

−1



−j



(4.17)

If necessary, Eqs. (4.14), (4.15), (4.16), and (4.17) can be used to evaluate

Eqs. (4.10) and (4.11) without the use of complex functions.

In practice, spectral data are held in a limited number N of “channels,” each

corresponding to electronic storage of a binary number. In this case j(v)isadiscrete

Fourier transform (DFT), deﬁned (Bracewell, 1978)by

j(n) = N

−1

m=N−1



m=0

J(m)exp(−2πimn/N) (4.18)

236 4 Quantitative Analysis of Energy-Loss Data

where J(m) is the spectral intensity stored in data channel m (m being linearly related

to energy loss) and the integer n replaces v as the Fourier “frequency.”

Because of

the sampled nature of the recorded data and its ﬁnite energy range, J(E) can be

completely represented in the Fourier domain by a limited number of frequencies,

not exceeding n = N − 1. Moreover, the spectral data J(E) are real (no imaginary

part), so that j

(−v) = j

(v), j

(−v) =−j

(v), and j

(0) = 0 (Bracewell, 1978).

Sometimes the negative frequencies are stored in channels N/2 to N, so these rela-

tions become j

(N − n) = j

(n), j

(N − n) =−j

(n), and j

(0) = 0. As a result,

only (N/2 + 1) real values and N/2 imaginary values of j(n) need be computed and

stored, requiring a total of N + 1 s torage channels for each transform. The require-

ment becomes just N channels if the zero-frequency value j

(0), representing the

“dc” component of J(E), is discarded (it can be added back at the end, after taking

the inverse transform). The fact that the maximum recorded frequency is n =N/2

(the Nyquist frequency) means that frequency components in excess of this value

ought to be ﬁltered from the data before computing the DFT (Higgins, 1976)in

order to prevent spurious high-frequency components appearing in the SSD (alias-

ing). In EELS data, however, this ﬁltering is rarely necessary because frequencies

exceeding N/2 consist mainly of noise (the spectra are oversampled).

Although the limits of integration in Eq. ( 4.7) extend to inﬁnity, the ﬁnite range

of the recorded spectrum will have no deleterious effect provided J(E) and its deriva-

tives have the same value at m =0 and at m = N−1. In this case, J(E) can be thought

of as being part of a periodic function whose Fourier series contains cosine and sine

coefﬁcients that are the real and imaginary parts of j(n). The necessary “continuity

condition” is satisﬁed if J(E) falls practically to zero at both ends of the recorded

range. If not J(E) should be extrapolated smoothly to zero at m=N − 1, using (for

example) a cosine bell function: A[1 −cos r(N − m − 1)], where r and A are con-

stants chosen to match the data near the end of the range. Any discontinuity in J(E)

creates unwanted high-frequency components which, following deconvolution, give

rise to ripples adjacent to any sharp features in the SSD.

In order to record all of the zero-loss peak, the origin of the energy-loss axis must

correspond to some nonzero channel number m

. The result of this displacement of

the origin is to multiply j(n) by the factor exp(2πim

n/N). However, Z(E) usually

has the same origin as J(E), so z(n) gets multiplied by the same factor and the effects

cancel in Eq. (4.10). In Eq. (4.11), where z(v) also occurs outside the logarithm, the

combined effect is to shift the recovered SSD to the right by m

channels, so that

its origin occurs in channel m = 2m

. To avoid the need for an additional phase

shift term in Eqs. (4.12) and (4.13), J(E) must be shifted, so that the center of the

zero-loss peak occurs in the ﬁrst channel (m = 0) before computing the transforms.

In that case, the left half of Z(E) must be placed in channels immediately preceding

the last one (m = N − 1).

The number of data channels used for each spectrum is usually of the form

N = 2

, where k is an integer, allowing a fast-Fourier transform (FFT) algorithm

As an example, the DFT of the unit-area Gaussian is exp(−π

4.1 Deconvolution of Low-Loss Spectra 237

to be used to evaluate the discrete transform (Brigham, 1974). The number of arith-

metic operations involved is then of the order of N log

N, rather than N

as in a

conventional Fourier transform program (Cochran, 1967), reducing the computation

time by a factor of typically 100 (for N =1024). Short (<50-line) FFT subroutines

have been published (e.g., Uhrich, 1969; Higgins, 1976).

The zero-loss peak is absent in the inverse transform of j

(n) but can be restored at

its correct location if an array containing Z(E) is stored separately. Z(E) can be useful

in the SSD because it delineates the zero-loss channel and provides an indication of

the specimen thickness and the energy resolution.

4.1.1.3 Thicker Samples

Strictly speaking, Eqs. (4.9), (4.10), (4.11), (4.12), and (4.13) do not specify a

unique solution for the single-scattering distribution; it is possible to add any multi-

ple of 2πi to the right-hand side of Eq. (4.15) and thereby change the SSD without

affecting the quantity in square brackets (i.e., the experimental data). This ambigu-

ity will cause problems if the true value of the phase θ (the imaginary part of the

logarithm) lies outside the range (normally − π to +π) generated by a complex

logarithm function, a condition that is liable to occur if the scattering parameter t/λ

exceeds π (Spence, 1979). If Eq. (4.17) is used, the value of θ is restricted to the

range −π/2 to π/2 and trouble may arise when t/λ > π/2.

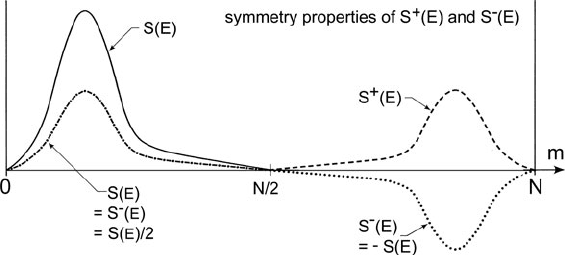
A solution to this phase problem (Spence, 1979) i s to avoid making use of the

imaginary part of t he logarithm. This would happen automatically if S(E)werean

even function (symmetric about m = N/2orm =0), since in this case s(v) has

no imaginary coefﬁcients (Bracewell, 1978). In practice, S(E)isnot even but can

always be written as a sum of its even and odd parts: S(E) = S

(E) +S

−

(E). If S(E)

is zero over one-half of its range (see Fig. 4.1), S(E) = 2S

(E) and it is sufﬁcient

to recover S

(E), thereby avoiding the phase problem. The necessary condition is

satisﬁed by doubling the length of the array, shifting the spectrum J(E) (before com-

puting its Fourier transform), so that the middle of the zero-loss peak occurs either

Fig. 4.1 Relationship between the single-scattering distribution S(E) and its even and odd parts,

(E)andS

–

(E), for the case where S(E) =0 in the range N/2 < m < N