Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems
Подождите немного. Документ загружается.

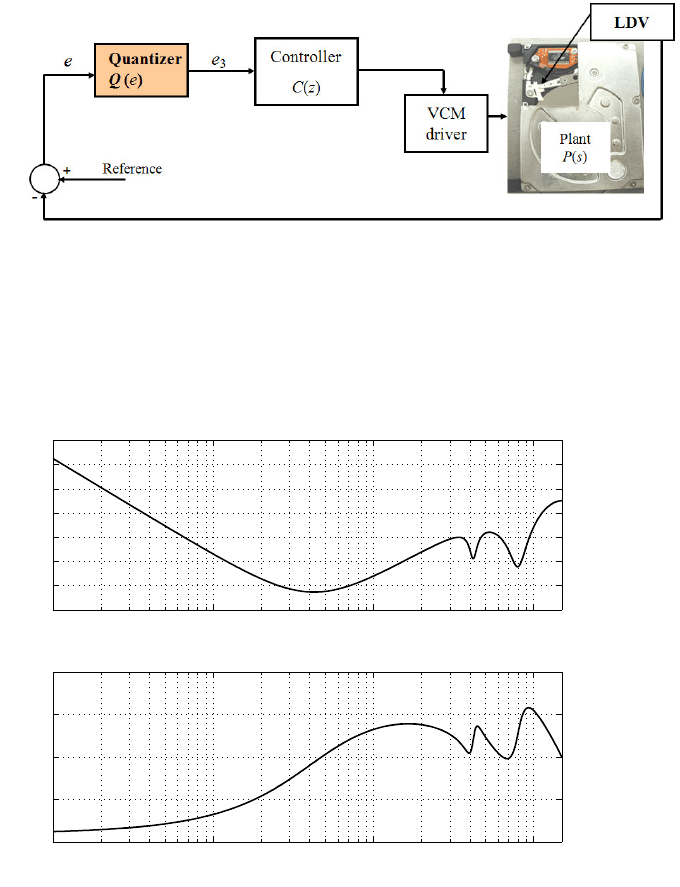
264 Modeling and Control of Vibratio n in Mechanical Systems
FIGURE 14.3
The servo loop in experiment.
10
1
10
2
10
3
10
4
−20
−15
−10
−5
0
5
10
15
Magnitude(dB)
10
1
10
2
10
3
10
4
−100
−50
0
50
100
Phase(deg)
Frequency(Hz)
FIGURE 14.4
Frequency response of the controller C(z).
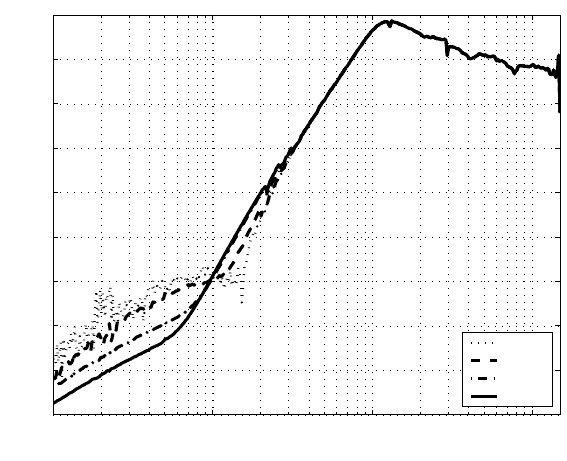
Quantization Effect on Vibration Rejection and Its Compensation 265
10
1
10
2
10
3
10
4
−80
−70
−60
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
0.05v
0.1v
0.5v
1v
FIGURE 14.5
Frequency response of the sensitivity function S(z) with different reference l evels
(i.e., actuator moving rang es are different).

266 Modeling and Control of Vibratio n in Mechanical Systems
14.3 Quant ization effect on error rejecti on
In this section, we investigate how the quantizer (14.1) wit h di fferent bits affects the
error rejectio n function, and show that the lower low-frequency disturbance rejection
reflected in the sensitivity function may also be caused by quantization in addition to
friction.
14.3.1 Quantizer frequency response measurement
Before we proceed to investigate the quantization effect on error r ej ection, we exam-
ine the transfer fu nction (14.4) for the quantizer (14.1) with different bits n through
the measurement of its frequency response.
The frequency response of e
3
over e in Figure 14.3 was measured via DSA by
injecting the swept sinusoidal signal as the reference signal. The qu antizer model
of the form in (14.1) with max(e) = 0.2 V and different resolution bits of n =
6, 8, 10 are investigated respectively. The dashed curves in Figures 14.6−14.8
are the corresponding measured frequency responses of Q(e). It is observed th at the
magnitude difference at frequencies less than 100 Hz between bits 6 and 8 are almost
10 dB and the phase difference is about 250 deg. From 200 Hz upwards, the quantizer
gains in the three cases are exactly unit y. Moreover, as the bit number increases, the
quantizer approaches unity gain. When bit n = 10, i t can be approximated as 1. The
frequency response when n = 12 is almost the same as that when n = 10, and thus
is omitted here.
14.3.2 Quantization effect on error rejection
Figur es 14.6−14 .8 show t hat the bit number n affects Q(e) mainly in low frequency
range. In addition, we shall see that Q(e) with lower bit number n will deterio rate
the error rej ecti on capability of the servo system in low frequency range.
The measured sensit ivity functions with different quantizer bits are shown in Fig-
ure 1 4.9, where the effect of the bit n on the low-frequency part can be seen. The
averaged difference of |S(z)| at the low-frequency range when the bit changes from
10 to 6 is about 10 dB. The trend is that the lower number of bits leads to a lower
effective magnitude of the compensated open loop, and thus higher |S(z)|, which
means poorer error rejection ability.
Note that a lower bit nu mber means that the known part due to the quantizati on
is less. When the error signal is too low for the A /D converter to differentiate, a
high level of error rejection can not be reflected in the sensitivity transfer function.
In Figure 14.5, the lowest sensitivit y function level at low frequencies is below −60
dB. This implies that a gain of at least 1000 requires more than 10 bit resolution.
Hence, as shown in Figure 14.9, for the two cases of n = 10 and n = 12, no obvious
impact on the sensitivity functions is seen.
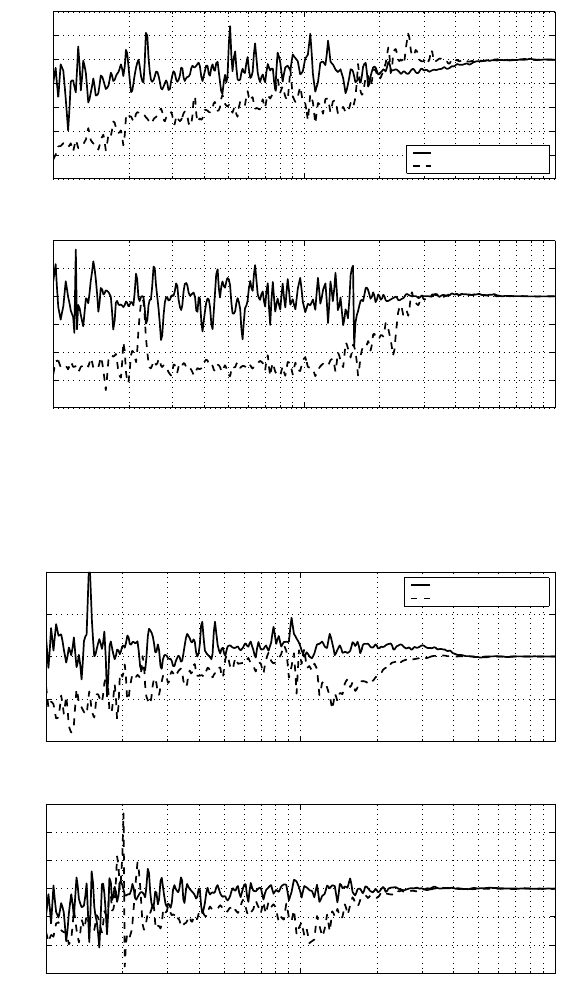
Quantization Effect on Vibration Rejection and Its Compensation 267
10
1
10
2
10
3
−50
−40
−30
−20
−10
0
10
20
Magnitude(dB)
After compensation
Before compensation
10
1
10
2
10
3
−400
−300
−200
−100
0
100
200
Frequency(Hz)
Phase(deg)
FIGURE 14.6
Frequency response of the quantizer before and after compensation (bit number n =
6).
10
1
10
2
10
3
−20
−10
0
10
20
Magnitude(dB)
After compensation
Before compensation
10
1
10
2
10
3
−150
−100
−50
0
50
100
150
Frequency(Hz)
Phase(deg)
FIGURE 14.7
Frequency response of the quantizer with compensation (bit number n = 8).
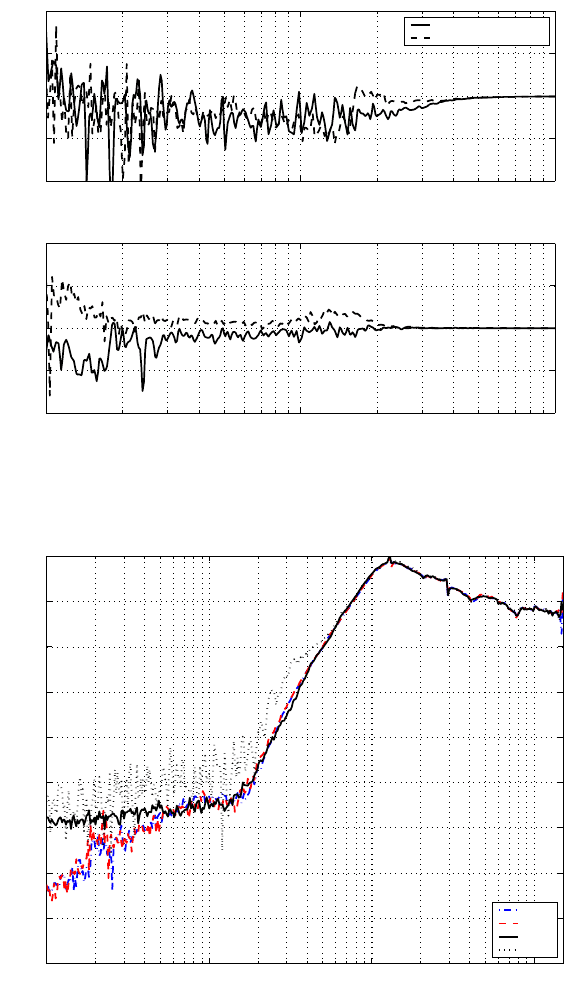
268 Modeling and Control of Vibratio n in Mechanical Systems
10
1
10
2
10
3
−10
−5
0
5
10
Magnitude(dB)
After compensation
Before compensation
10
1
10
2
10
3
−200
−100
0
100
200
Frequency(Hz)
Phase(deg)
FIGURE 14.8
Frequency response of the quantizer with compensation (bit number n = 10).
10
1
10
2
10
3
10
4
−80
−70
−60
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
n=12
n=10
n=8
n=6
FIGURE 14.9
Measured sensitivity function S
Q
(z) with different bits n.
Quantization Effect on Vibration Rejection and Its Compensation 269
We t ake |S
Q
(f)| at f = 10 Hz as the representative value of |S
Q
(z)| at low
frequencies. Figure 14.10 shows the relation of |S
Q
(f)| versus bit number n at
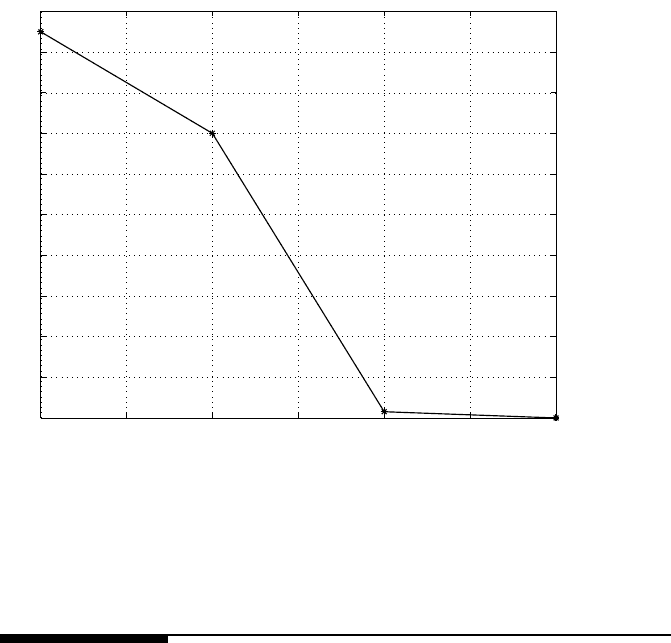
f = 10 Hz, which is d ecreasing dramatically until n = 10. This means that bit
number n = 10 is necessary for satisfactory performance. Approximately |S
Q
(z)| =
0.4604n
3
−12.1 375n
2
+99.2 833n−303.2000. Similar to Figure 14.5, |S
Q
(z)| with
a fixed bit number n also changes with plant excit at ion levels. The trend of |S
Q
(z)|
with the bit number n is almost the same for each excitation level.
6 7 8 9 10 11 12
−64
−62
−60
−58
−56
−54
−52
−50
−48
−46
−44
Bit n
|S(f)|
f=10
FIGURE 14.10
Sensitivity function |S
Q
(f)| with f = 10 Hz versus bit n.
14.4 Co mpensation of quantization effect on error rejection
In this sectio n, a scaling method is used to compensate fo r the effect of the quantizer
on the sensitivity function at low f requencies. The compensation scheme is shown in
Figur e 14.11. When the error signal amplitude is less than a threshold δ, it is scaled
up by a factor a > 1, and then scaled down by the factor a
−1
after undergoing quan-
tization. The method of choosing t he thr eshold δ and the scaling factor a is ill ustrated
in Figure 14.12. M is the value at the beginning point where the quantization effect
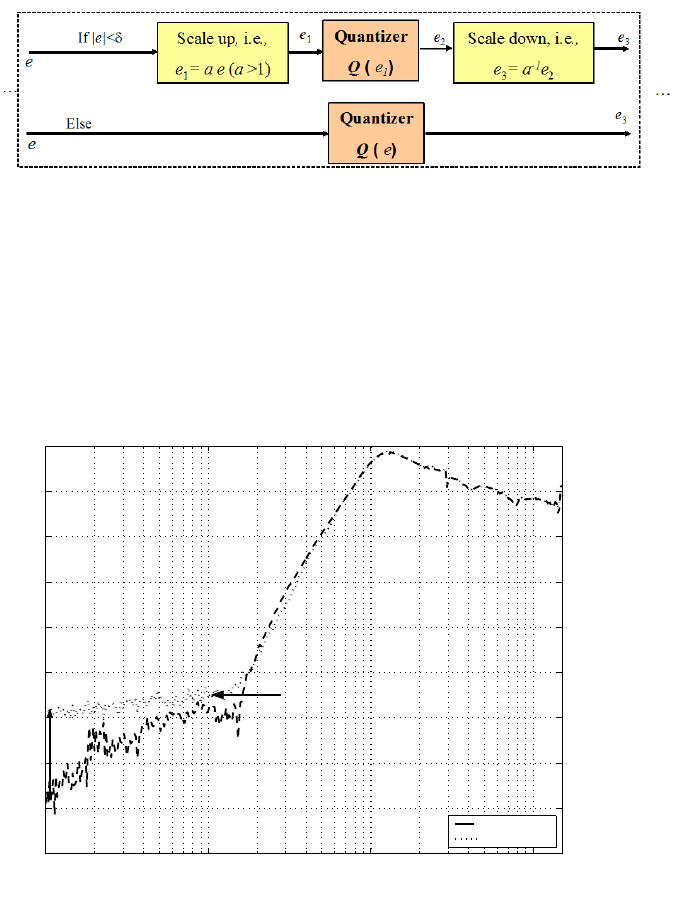
270 Modeling and Control of Vibratio n in Mechanical Systems
FIGURE 14.11
Compensation scheme of quantization effect.
can be seen obvio usly. D is the biggest difference between S
Q
and S. δ and a can
be generally chosen as follows.
δ = 10
M/20
· reference, a = 10
D/20
. (14.5)
10
1
10
2
10
3
10
4
−80
−70
−60
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
Target S
Measured S
Q
M
D
FIGURE 14.12
Choo sing the threshold δ and the scaling factor a.
The compensati on is carried out for three cases wi th n = 6, 8, and 10 respectively,
and the improvement of the error rejection after compensation will be di scussed.
A. n = 6
Quantization Effect on Vibration Rejection and Its Compensation 271
In this case, from the sensitivity function in Figure 14.9, δ and a are obtained as
δ = 10
−40/20
· 50 mV = 0.5 mV, a = 10
18/20
= 8.
Figur e 14.6 shows the impr oved frequency response of the quantizer after com-
pensation. The sensitivity function improvement after compensation in the low fre-
quency range is shown in Fi gures 14.9 and 14.13. There is no further improvement
when a is increased. When a = 5, the resul t is as good as when a = 8, which means
that the optimal value of a is roughly between 5 and 8.
10
1
10
2
10
3
10
4
−80
−70
−60
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
n=10
n=8
n=6
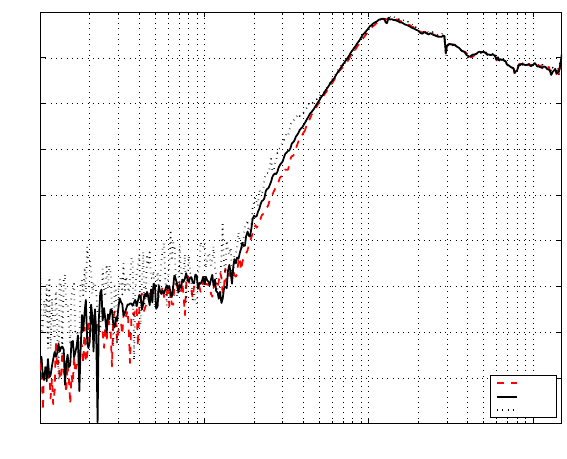
FIGURE 14.13
Sensitivity function with quantization compensation.
B. n = 8
When n = 8,
δ = 10
−48/20
· 50 mv = 0.2 mv, a = 10
15/20
= 5.6.
Figur es 14.7 and 14.13 show the obvious i mprovement o f the quantizer and t he
sensitivit y function after compensation. When a is increased to 10 and above, no
furt her improvement is observed. Thus the best value of a can be chosen around 5.6.
C. n = 10
In the case with bit n = 10,
δ = 10
−48/20
· 50 mV = 0.2 mV, a = 10
10/20
= 3.

272 Modeling and Control of Vibratio n in Mechanical Systems
TABLE 14.1
Quantizati on and friction effect
Quantizer bit n 6 8 10
Actually measured |S|
f=10Hz
(dB) −45 −50 −65
Compensated quantization effect ( dB) 13 18 4
Estimated |S|
f=10Hz
with friction effect (dB) −58 −68 −69
No obvious difference can be seen in Figure 14.8. When compared with Figur e
14.9, Figure 14.13 shows the obvio us improvement of the sensi tivity function after
compensation. When a = 6, t he result is almost the same. As a is increased to 10,
the result becomes worse. Thus in this case a = 3 can be chosen as one of the best
scaling factors.
It can be seen from Figure 14.13 that aft er compensation, |S
Q
(z)|is much closer to
|S(z)| in the dotted line in Figure 14.5, which is measured without the quantizer and
thus considered as subjected to nonlinear friction effect only, e.g., |S(z)|
f=10Hz
=
−69 dB wi th friction effect alone. From Figure 14.13, we can also see that instead
of bit number n = 10 p reviously shown in Section 14.3.2 without compensation, bit
number n = 8 is adequate with th e compensation for a similar performance.
It has been shown that the low frequency range of the sensitivity function is also
affected by quantization in addition to actuator pivot fri ction. When the qu antiza-
tion effect is compensated for sufficiently, the low frequency portion of t he sensi-
tivit y fun ct ion can be regarded as the estimated effect from friction alone. Thus, by
comparing the compensated and the uncompensated |S
Q
(z)| with Figure 14.13, the
quantization and the friction effect on S
Q
(z) can then be differentiated and shown in
Table 14.1. We can see that the estimated frictio n effect for n = 6 is not as accurate
as the other two cases. This is because the compensation for n = 6 is insufficient,
as seen in Figure 14.13. In th is situation, a multi-st age scaling, i.e., a = a
i
for
δ
i1
< |e| < δ
i2
, i = 1, 2, ... , may be necessary.
To th is end, the scaling compensation scheme is cond ucted for quantization com-
pensation in the disk drive. The series of results demonstrates that the compensation
scheme is effective in improving the sensitivity function in the low frequency range
without influencing other frequencies. Additional ly, it is noted that the implement a-
tion of the scheme is simple and therefore incurs low cost.
14.5 Co nclusion
The quantization effect on the closed-loop system performance has been investi-
gated. The frequency responses of t he quantizers with different bits have been mea-
sured and analy zed. Its effect on the error rejection function or sensitivity function
at low frequencies has shown that the rejection ability of the servo loop for l ow
Quantization Effect on Vibration Rejection and Its Compensation 273
frequency disturbances is relevant to the quantizer in addition to the pivot friction.
Moreover, a simple and l ow cost scaling scheme has been used to compensate for the
effect of the quantizer. With sufficient compensation, the effects due t o quantization
and fri ct ion can be differentiated, and thus the friction and the quantization impact on
the system performance such as disturbance rejection capability can be t reated sepa-
rately. Through the proposed quantization model and measurement methodology, a
suitable bit resolution for the quantizer can be easily identified w hile the pivot fric-
tion nonlinearity effect can be decoupled and tackled for more effective closed-loop
system control.
