Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems
Подождите немного. Документ загружается.

224 Modeling and Control of Vibratio n in Mechanical Systems
0 0.05 0.1 0.15 0.2 0.25 0.3
−8
−6
−4
−2
0
2
4
6
8
x 10
−3
Time(sec)
Amplitude of disturbance d1 and its estimate (µm)
d
1
estimate of d
1
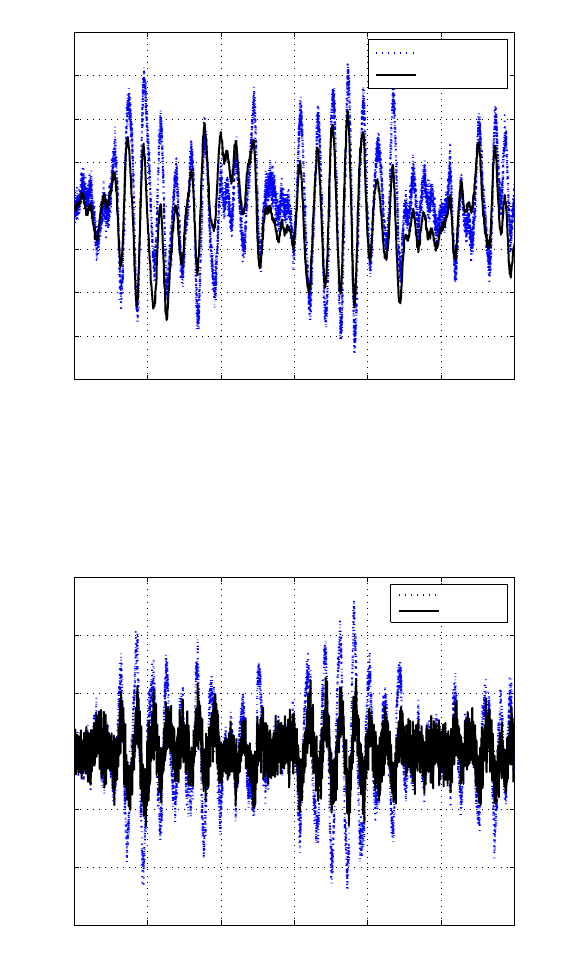
FIGURE 11.6
Distu rbance d
1
.
0 0.05 0.1 0.15 0.2 0.25 0.3
−0.03
−0.02
−0.01
0
0.01
0.02
0.03
Time(sec)
Amplitude of error e (µm)
No DOB
With DOB
FIGURE 11.7
Error sig nal e.

H
∞
-Based Desig n for Disturbance Observer 225
10
2
10
3
10
4
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
No DOB
With general DOB
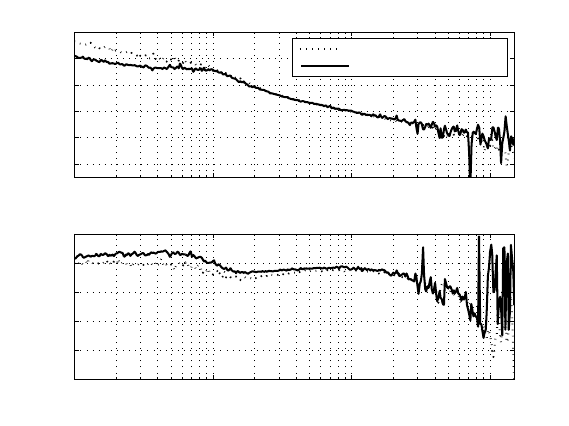
FIGURE 11.8
Measured sensitivity functions without and with the general disturbance observer.
10
1
10
2
10
3
10
4
−40
−20
0
20
40
60
Magnitude(dB)
10
1
10
2
10
3
10
4
−500
−400
−300
−200
−100
0
Phase(deg)
Freuqency(Hz)
Nominal
with the general DOB
FIGURE 11.9
Comparison of T
EQ−OL
about the general disturbance observer.
226 Modeling and Control of Vibratio n in Mechanical Systems
10
1
10
2
10
3
10
4
−40
−20
0
20
40
60
Magnitude(dB)
10
1
10
2
10
3
10
4
−500
−400
−300
−200
−100
0
Phase(deg)
Freuqency(Hz)
Nominal
with the conventional DOB
FIGURE 11.10
Comparison of T
EQ−OL
about conventional distu rbance observer.

12
Two-Dimensional H
2
Control for Error
Minimization
12.1 Introduction
The H
2
optimal control for 1-D systems is a cl assical problem in linear systems
theory. Its objective is to minimize the error energy of the system when the system is
subject to a un it impulse inp ut or, equivalently, a white noise input of unit variance.
Because of thi s analytically and p ractically meaning ful specification, the H
2
problem
and solution has been well studied and applied for several decades. Recently, the
H
2
control pro blem has been studied for 2-D syst ems and a sufficient condition for
the evaluation of 2-D system H
2
performance in terms of LMIs is derived [1 39].
Using the condition, a systematic method for the design of the H
2
controller for 2-
D systems in terms of LMIs has been developed. The developed 2-D H
2
control
design method is of great importance to those systems that have 2-D behavior and
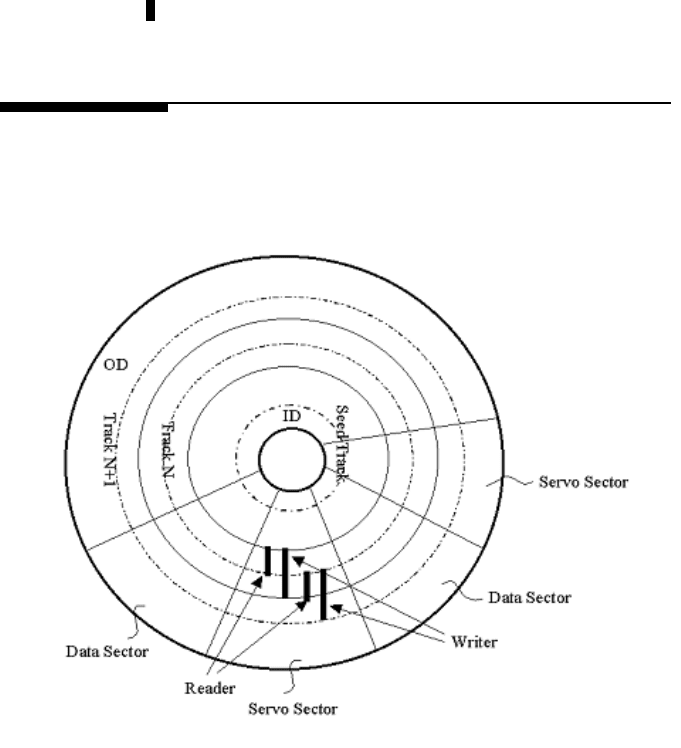
can be modeled using 2-D linear system models. Self-servo track writer (SSTW)
for data storage devices is one of these systems [17]. In the self-servo tr ack wri ting,
due to vibrations and noise the servo controll er causes the actuator to follow the
resulting non-circular trajectory in the next burst writing step, so that the new bursts
are written at locations reflecting the errors present in the preceding track via the
closed-loo p response of the servo loop, as well as in th e present track. Consequently,
each step in the process carries a “memory” of all p receding track shape errors.
This “memory” depends on the particular closed-loop response of the servo loop.
Because of the interdependency of propagation tracks, track shape errors may be
amplified from one track to the next through the closed-loop response when writing
the propagation tracks. Thus self-servo writing systems must provide a means of
accurately writing servo-patterns while controlling the propagation of track shape
errors. Therefore, error propagation contain ment is critically important. The target
of preventing error propagation is to reject the track shape error due to track non-
circularity recorded in propagated tracks so that th e circul ar concentric tracks are
achieved in every propagation trace.
In this chapter we describe the SSTW process with a two-dimensional (2-D) model.
Then the error propagation containment problem of the SSTW process is formulated
as a 2-D stabilization problem. Instead of the conventional f eedforw ard con trol, the
2-D stabilizing control is able to prevent the error propagation. Furthermore, the
227

228 Modeling and Control of Vibratio n in Mechanical Systems
TMR minimization problem of the SSTW pr ocess is formulated as a 2-D H
2
con-
trol problem. A 2-D H
2
controller is design ed which is able to prevent the error
propagation and minimize the TMR.
12.2 2 -D stabilization control
We consider the following 2-D system model [138]:
x
h
(i + 1, j)
x
v
(i, j + 1)
= A
x
h
(i, j)
x
v
(i, j)
+ B
1
w(i, j) + B
2
u(i, j), (12.1)
y(i, j) = C
1
x
h
(i, j)
x
v
(i, j)
+ D
11
w(i, j) + D
12
u(i, j), (12.2)
e(i, j) = C
2
x
h
(i, j)
x
v
(i, j)
+ D
21
w(i, j) + D
22
u(i, j), (12.3)
where x
h
∈ R
n
1
, x
v
∈ R
n
2
, w(i, j) ∈ R
q
, u(i, j) ∈ R
m
, y(i, j) ∈ R
p
and
e(i, j) ∈ R
l
are, respectively, the horizontal state, the vertical state, the disturbance
input, the control input, the controlled output, and the measurement of the plant.
Let
x(i, j) =
x
h
(i, j)
x
v
(i, j)
, (12.4 )
the above system is equivalent to
x(i + 1, j + 1) = A
1
x(i, j + 1) + A
2
x(i + 1, j)
+B
11
w(i, j + 1) + B
12
w(i + 1, j)
+B
21
u(i, j + 1) + B
22
u(i + 1, j), (12.5)
y(i, j) = C
1
x(i, j) + D
11
w(i, j) + D
12
u(i, j), (12.6 )
e(i, j) = C
2
x(i, j) + D
22
u(i, j) (12.7)
where
A
1
=
I
n
1
0
0 0
A, A
2
=
0 0
0 I
n
2
A,
B
k1
=
I
n
1
0
0 0
B
k
, B
k2
=
0 0
0 I
n
2
B
k
, k = 1, 2. (12.8)
Intr oduce the following 2-D output feedback contr oller C(z
1
, z
2
):
x
c
(i + 1, j + 1) = A
c1
x
c
(i, j + 1) + A
c2
x
c
(i + 1, j)
+B
c1
e(i, j + 1) + B
c2
e(i + 1, j), (12.9)
u(i, j) = C
c
x
c
(i, j) + D
c
e(i, j). (12.10)

Two-D imensional H
2
Control for Error Minimization 229
Associated with the 2-D controller (12.9)−(12.10), the 2-D stabilization prob-
lem i s stat ed as foll ows: for the 2-D system (12.1)−(12.3) or (12.5)−(12.7) with
w(i, j) = 0, design a dynamic output feedback controller of the form in (12.9)−(12.10)
such that the resulting closed-loop SSTW servo system is asymptot ically st able.
Define
Z = D
c
CR + C
c
Ξ
T
, V
k
= SB
2k
D
c
+ ΛB
ck
, (12.11)
U
k
= S(A
k
+ B
2k
D
c
C)R + SB
2k
C
c
Ξ
T
+ ΛB
ck
CR + ΛA
ck
Ξ
T
, k = 1, 2,
(12.1 2)
where R > 0, S > 0 and Ξ and Λ are invertible matrices satisfying ΞΛ
T
= I −RS.
THEOREM 12.1
[136] C onsider the 2-D system (12.5)−(12.7). Then, there exists a full order
output feedback controller of the form in (12.9)−(12.10) that asymptotically
stabilizes the system (12.5)−(12.7) if there exist matrices R > 0, S > 0,
˜
Ω
X
> 0, D
c
, U
k
, V
k
(k = 1, 2) and Z such that the following LMI holds:
−
˜
Ω
X
0
˜
Ω
T
A1
0 −(
˜
Ω
F
−
˜
Ω
X
)
˜
Ω
T
A2
˜
Ω
A1
˜
Ω
A2
−
˜
Ω
F
< 0 (12.13)
where
˜
Ω
F
=
S I
I R
,
˜
Ω
A1
=
SA
1
+ V
1
C U
1
A
1
+ B
21
D
c
C A
1
R + B
21
Z
,
˜
Ω
A2
=
SA
2
+ V
2
C U
2
A
2
+ B
22
D
c
C A
2
R + B
22
Z
. (12.14)
In this situation, the controller parameters of (12.9)−(12.10) can be given by
C
c
= (Z − D
c
CR)Ξ
−T
, B
ck
= Λ
−1
(V
k
− SB
2k
D
c
), (12.15)
A
ck
= Λ
−1
[U
k
−S(A
k
+ B
2k
D
c
C
2
)R − SB
2k
C
c
Ξ
T
− ΛB
ck
C
2
R]Ξ
−T
, k = 1, 2.
(12.1 6)
12.3 2 -D H
2
control
Let T
yw
: w → y denote the closed-loop system subject to the white noise w. The
H
2
norm of T
yw
is approximately given by
kT
yw
k
2
=
v
u
u
t
1
L
1
K − 1
L,K−1
X
i, j=1
y(i, j)
2
(12.1 7)
230 Modeling and Control of Vibratio n in Mechanical Systems
where L and K are large enough. The control desig n prob lem to minimize the 2-
D H
2
norm is stated as follows: find a 2-D outpu t feedback controller of the form
in (12.9)−(12.10) for the 2-D system (12.1)−(12.3) or (12.5)−(12.7) such that the
closed-loo p system is stabl e and the H
2
performance kT
yw
k
2
is minimized.
An LMI app roach will be given as follows to design a 2-D H
2
controller for the
2-D system (12.1)−(12.3) such that the cl osed-loop system is stable and the error is
minimized.
THEOREM 12.2
[139] The 2-D H
2
control problem for the plant (12.1)−(12.3) is s olvable if
there exist matrices S > 0, Θ, Λ, Γ, D
c
and block-diagonal matrices X =
diag{X
h
, X
v
}, Y = diag{Y
h
, Y
v
}, M = diag{M
h
, M
v
}, H
11
= diag{H
h
11
,
H
v
11
} > 0, H
22
= diag{H
h
22
, H
v
22
} > 0, and H
12
= diag{H
h
12
, H
v
12
}, of appro-
priate dimensions, such that
H
11
∗ ∗ ∗ ∗
H
T
12
H
22
∗ ∗ ∗
XA + ΓC
2
Θ X + X
T
− H
11
∗ ∗
A + B
2
D
c
C
2
AY
T
+ B
2
Λ I + M
T
−H
T
12
Y + Y
T
−H
22
∗
C
1
+ D
12
D
c
C
2
C
1
Y
T
+ D
12
Λ 0 0 I
> 0,
(12.1 8)
S ∗ ∗ ∗
XB
1
+ ΓD
21
X + X
T
− H
11
∗ ∗
B
1
+ B
2
D
c
D
21
I + M
T
−H
T
12
Y + Y
T
−H
22
∗
D
11
+ D
12
D
c
D
21
0 0 I
> 0, (12.19)
T race(S) < λ
2
, (12.2 0)
are satisfied. If the above stated conditions are satisfied, a feasible H
2
con-
troller is given by
x
h
c
(i + 1, j)
x
v
c
(i, j + 1)
= A
c
x
h
c
(i, j)
x
v
c
(i, j)
+ B
c
e(i, j), x
h
c
∈ R
n
h
, x
v
c
∈ R
n
v
, (12.21)
u(i, j) = C
c
x
h
c
(i, j)
x
v
c
(i, j)
+ D
c
e(i, j), (12.2 2)
with
A
c
= U
−1
[Θ − X(A + B
2
D
c
C
2
)Y
T
− XB
2
C
c
V
T
−UB
c
C
2
Y
T
]V
−T
,(12.23)
C
c
= (Λ − D
c
C
2
Y
T
)V
−T
, B
c
= U
−1
(Γ −XB
2
D
c
), (12.24)
where U = diag{U
h
, U
v
} and V = diag{V
h
, V
v
} satisfy XY
T
+ U V
T
= M .
REMARK 12.1 The solution of the 2-D controller in the above theorem
is in terms of LMIs which can be efficiently solved by convex optimization just
Two-D imensional H
2
Control for Error Minimization 231
like other 1-D control problems involving LMIs. In [13 9], it is proved that if
there exist sol utions X, Y , M, D
c
, S > 0, Θ, Λ, Γ, H
11
, H
22
, and H
12
for
the LMIs (12.18)-(12.20), M − XY
T
is invertible. From U V
T
= M − XY
T
,
nonsingula r matrices U and V can b e computed. Then, the computation of
the controll er parameters C
c
, A
c
, B
c
can be carried out by solving (12.23)
and (12.2 4).
12.4 SSTW process and modeling
FIGURE 12.1
SSTW pro cess.
The process of self-servo writing is shown in Figure 12.1 and is generally known
to involve th e following distinct steps [135]: w riting some tracks or at least on e track
called seed tracks; reader reads back th e seed track and writer writes actual product
servopattern for the next track based o n th e readback signal; writing servopattern f or
232 Modeling and Control of Vibratio n in Mechanical Systems
the next track based on the readback signal from the previous written track till the
whole process is completed. During the process, SSTW generates radial informa-
tion progr essively to deploy servopattern. The radial error in track N is inevitably
compounded to the following tracks: tracks N + 1, N + 2, ···. This l eads to error
propagation in SSTW.
In self-servo track writing, track shape errors such as non-circularity are intro-
duced by mechanical disturbances, spindle motor vibration and other factors when
writing the propagation tracks. The servo controller causes the actuator to foll ow
the resulting non-circular trajectory in the next burst writing step, so that the new
bursts are written at locations reflecting the error s present in the preceding step via
the closed-loop response of the servo lo op, as well as in the present step. Conse-
quently, each step in the process carries a “memory” of all preceding track shape
errors. This “memory” depends on the particular closed-loop response of the servo
loop. Self-servo wri ting systems must pr ovide a means of accurately w riting ser-
vopatterns while controlling the propagation o f track shape erro rs.
12.4.1 SSTW servo loop
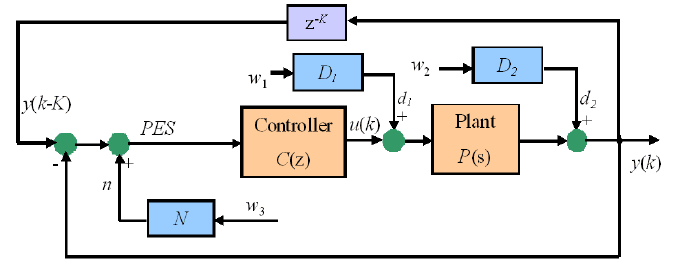
FIGURE 12.2
SSTW servo l oop with distur bances and no ise mod el s.
Figur e 12.2 shows the SSTW servo loop with disturbances and noises. D
1
(s),
D
2
(s), and N (s) are respectively the models of disturbances d
1
, d
2
and noise n.
y(k) is the position of the wr ite head with respect to a perfectly circular track o n the
disk and P ES(k) is the position error signal. Let T
p
be the rotational period of the
disk, and T
s
be the sampling rate of the position error signal. Then the sector number
K = T
p
/T
s
. y(k − K) represents the track pro file of the previous tr ack. Similarly,
P ES(k −K) represents the posit ion error when writing the previous track. The read
head follows on the track y(k −K) which is the reference input for the SSTW servo
system, i.e., one revol ution of y (k) becomes the reference of the next written track
Two-D imensional H
2
Control for Error Minimization 233
or a few subsequent tracks due to the action of self-servo writing.
It follows from Figure 12.2 that
y(k) = T (z)y(k −K) + P (z)S(z)d
1
(k) + S(z)d
2
(k) + T (z)n(k), (12.25)
where S(z) = 1/(1 + P (z)C(z)) is the sensitivity function, T (z) = 1 −S(z) is the
closed-loo p transfer function. The typical closed-loop transfer function will amplify
the error at the frequency where its magnitude is more than 0 dB. In other words,
these fr equ ency components in disturbances or noise wi ll b e ampli fied during prop-
agation, while others will compound to following tracks and decay gradually. With
the same disturbance models D
1
(s) and D
2
(s) and noise model N (s) as in Chapter
11, Figure 12.3 shows PES NRRO in the time domain and its σ value versus track
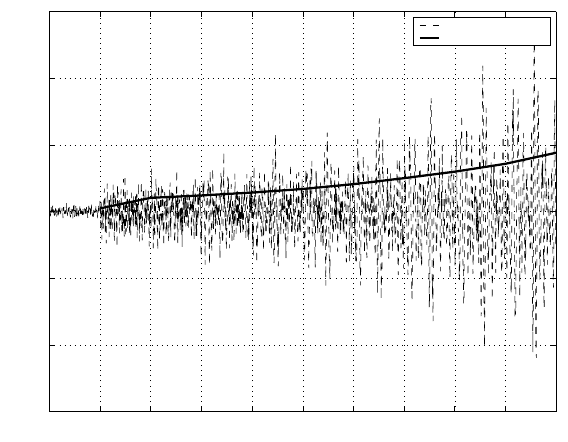
number when a 1-D feedback controller C(z) is used in the closed loop. The error
propagation mentioned previously is clearly observed. Hence the error propagation
problem must be addressed in the servo control design for SSTW.
0 1 2 3 4 5 6 7 8 9 10
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
Track number
PES and σ of PES
Position error signal
Sigma value
FIGURE 12.3
PES NRRO and its σ values versus track number during propagation. (The time
sequence and the σ value increase with the track number.)
12.4.2 Two-dimensional model
For the 2-D modeling, the following notations are used:
