Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems
Подождите немного. Документ загружается.

204 Modeling and Control of Vibration in Mechanical Systems
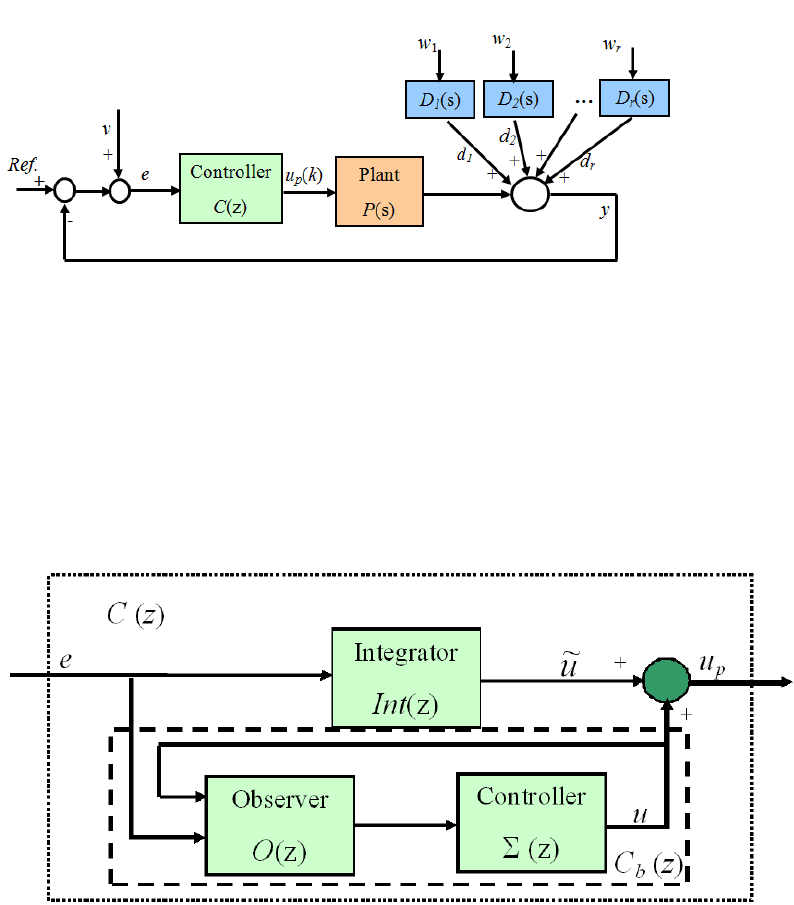
FIGURE 10.2
Control loo p with injected disturbances at different frequencies.
FIGURE 10.3
Control structure.
Blending Control for Multi-Frequency Disturba nce Rejection 205
y
2
(k) = C
2
x(k) + D
2
u(k), (10.41)
···
y
r
(k) = C
r
x(k) + D
r
u(k), (10.42)
e(k) = C
e
x(k) + D
e
u(k) + v(k), (10.43)
where x =
x
T
p
˜u
T
x
T
d
1
x
T
d
2
··· x
T
d
r
T
∈ R
n
x
, u(k) ∈ R
n
u
, y
i
(k) ∈ R
p
i
, w
i
(k) ∈
R
q
i
, n
x
= n
p
+ 1 +
r
P
i=1
n
d
i
, n
u
= 1 , p
i
= 1, q
i
= 1,
A =
A
p
B
p
0 0 ··· 0
−
˜
kC
p
1 −
˜
kD
p
˜
kC
d
1
˜
kC
d
2
···
˜
kC
d
r
0 0 A
d
1
0 ··· 0
0 0 0 A
d
2
··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 0 ··· A
d
r
, B =
B
p
−
˜
kD
p
0
0
.
.
.
0
, (10.44)
E
1
=
0
−
˜
kD
d
1
B
d
1
0
.
.
.
0
, E
2
=
0
−
˜
kD
d
2
0
B
d
2
.
.
.
0
, ···, E
r
=
0
−
˜
kD
d
r
0
0
.
.
.
B
d
r
, (10.45)
C
1
=
−C
p
−D
p
−C
d
1
0 ··· 0
, D
1
= −D
p
, (10.46)
C
2
=
−C
p
−D
p
0 −C
d
2
··· 0
, D
2
= −D
p
, (10.47)
C
r
=
−C
p
−D
p
0 0 ··· −C
d
r
, D
r
= −D
p
, (10.48)
C
e
=
−C
p
−D
p
−C
d
1
−C
d
2
··· −C
d
r
, D
e
= −D
p
. (10.4 9)
Note that the measurement error signal e in (10.43) includes all distur bance out-
puts y
i
, i = 1, 2, ···, r.
10.3.2 Controller desig n via the control blending technique
In this section, we present how to design the controller C(z) by using the control
blending technique. Before the blending, the H
2
optimal control method will be
used to design a static st at e feedback controller to minimize the error caused by each
disturbance. Subsequentl y, the blending techniq ue will be utilized to y ield one single
dynamic state feedback controll er that is able to reject all disturbances. Next a state
observer will be designed to facilitate the state feedback controller with the mea-
surement signal. Finally, the SISO (single input and single output) output feedback
controller C
b
(z) will be given based on the dynamic state feedback controller and
the state observer.
Denote the dynamic state feedback controller by
Σ(z) : x
s
(k + 1) = A
s
x
s
(k) + B
s
x(k), (10.50)
206 Modeling and Control of Vibratio n in Mechanical Systems
u(k) = C
s
x
s
(k) + D
s
x(k). (10.51)
This dynamic state feedback controller is designed fol lowing Procedure 10.1,
where K
i
in step 1 is designed based on the H
2
optimal control method, which
is described as f ollows.
Let K
i
, i = 1, 2, ···, r be the static state feedback controllers each of which
asymptotically stabilizes the plant and minimizes the H
2
norm of the transfer func-
tion from w
i
to y
i
. K
i
can therefore be ob tained by the following optimization:
min T race(S
i
)
subject to the LMIs
−P
i
∗ ∗
P
i
A
T
+ W
T
i
B
T
−P
i
∗
0 C
i
P + D
i
W
i
−1
< 0, (10.52)
−S
i
∗
E
i
−P
i
< 0. (10.5 3)
With t he solved W
i
and P
i
, K
i
is obtained as
K
i
= W
i
P
−1
i
. (10.54)
Next, a dyn amic state feedback controller of the form ( 10.50)−(10.51) is designed
based on Procedure 10.1. Si nce only the measurement is available for f eedback, a
state observer, as in Figu re 10.3, is needed to facilitate the controller Σ(z). The state
observer O(z) is designed as follows.
ˆx(k + 1) = A
o
ˆx(k) + [B
o1
B
o2
]
u(k)
e(k)
, (10.5 5)
y
o
(k) = C
o
ˆx(k) + D
o
u(k)
e(k)
, (10.56 )
where
A
o
= A − ALC
e
, B
o1
= B, B
o2
= AL, (10.57)
C
o
= I, D
o
= 0, (10.58)
L = dlqe(A, E, C
e
, Q, R), E is as in (10.6), Q = I, and R = σ
2
v
.
The overall control ler C(z) is then given by
A
c
=
A
s
B
s
C
o
B
o1
C
s
A
o
+ B
o1
D
s
C
o
, B
c
=
0
B
o2
, (10.5 9)
C
c
=
C
s
D
s
C
o
, D
c
= 0 . (10.60)
Blending Control for Multi-Frequency Disturba nce Rejection 207
10.4 Simulation and experimental results
The disk drive under consideration is a 1.8-inch small hard disk drive with a spindle
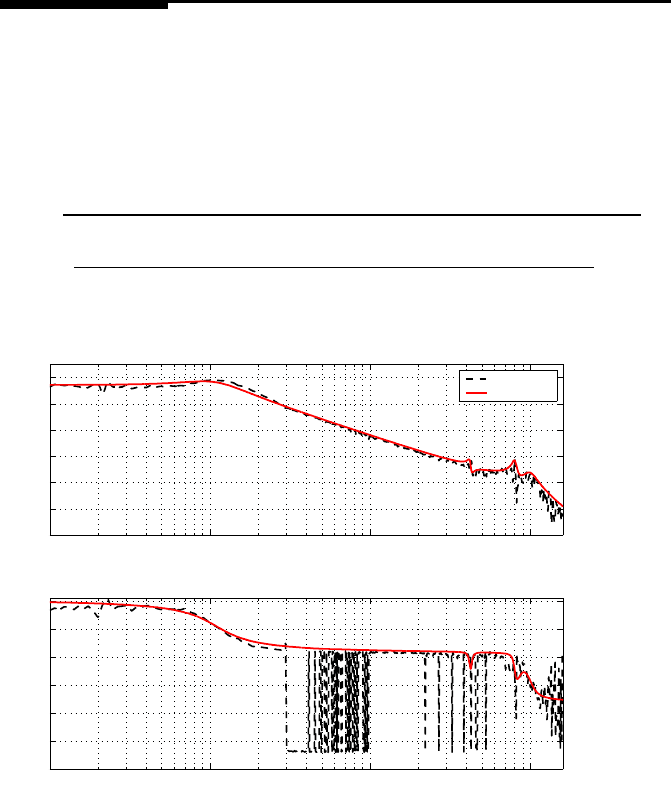
motor ro tational speed of 4200 RPM. Figure 10.4 shows the frequency response of
the VCM actuato r. The VCM actuator model P (s) is described by
P (s) =
8.326628 × 10
17
(s
2
+ 1081s + 7.3 × 10
8
)(s
2
+ 6635s + 2.852 ×10
9
)
(s
2
+ 552.9s + 4.777 × 10
5
)(s
2
+ 1056s + 6.964 × 1 0
8
)
×
1
(s
2
+ 2815s + 2.527 × 1 0
9
)(s
2
+ 1.131 × 10
4
s + 3.948 × 10
9
)
. (10.61)
10
1
10
2
10
3
10
4
−60
−40
−20
0
20
40
60
Gain [dB]
Measured
Modeled
10
1
10
2
10
3
10
4
−600
−500
−400
−300
−200
−100
0
Frequency [Hz]
Phase [degree]
FIGURE 10.4
Frequency response of the VCM actuator.
10.4.1 Rejecting high-frequency disturbances
In this sectio n, controll er C(z) will be designed to reject a few disturbances with
frequencies higher than bandwid th. First, two disturbances will be rejected, and
next, three disturbances are to be attenuated simultaneously.
208 Modeling and Control of Vibratio n in Mechanical Systems
We consider two disturbances at frequencies 4 kHz and 8 kHz which are the res-
onance frequencies of the plant as shown in Figure 10.4. By fitting the model in
(10.37), we have ω
1
= 2π4000, ξ
1
= 0.085, ζ
1
= 0.6, k
d1
= 20 for D
1
(s), and
ω
2
= 2π8000, ξ
2
= 0.01, ζ
2
= 0 .6, k
d2
= 43 for D
2
(s).
Take k
i
= 100 · T
s
. The parameters in (10.19) of Σ(z) are o btained by the design
procedure outlined in the last section. With Σ(z), the observer O(z) (10.55)−(10.56),
we have cont roller C
b
(z) by (10.59)−(10.60). Incorp orated with an i ntegrator, a 27 th
order C(z) is obtained. After simple o rder reduction by canceling close zeros and
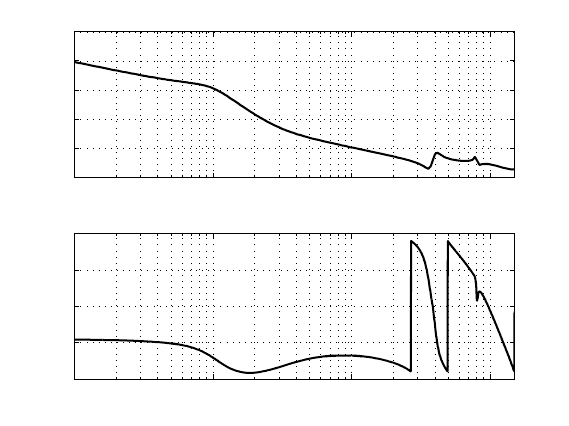
poles, C(z) can be redu ced to 14t h order. The final controller C(z) leads to the fre-
quency response of the open-loop P (z)C(z) as shown in Fig ure 10.5. The open-loop
bandwidth i s 1 kHz. The simulated sensitivity function S(z) = 1/(1 + P (z)C(z))
is shown in Figure 10.6, where there are two obvious rejection (i.e., | S(z)| < 1)
frequency ranges around 4 kHz and 8 kHz.
Rejection capability i n terms of | S(z)| for D
i
(i = 1, 2 ) can be changed b y
adjusting k
di
and ξ
i
. More simulations show that the change of |S(z)| for D
1
at 4
kHz leads to slight variation of |S(z)| for D
2
at 8 kHz, while the change of |S(z)|
for D
2
at 8 kHz affects more on |S(z)| around 4 kH z. Moreover, changing k
d2
will
affect rejection at 4 kHz more than changing damping ξ
2
.
The controller is implemented via dSpace 110 3 wit h the utilizati on of LDV to
measure the displacement of t he actuator. The sensitivit y function S(z) of the clo sed
control l oop is measured via DSA and plotted in Figure 1 0.7, which agrees well with
the simulated one (the dashed curve).
10
1
10
2
10
3
10
4
−20
0
20
40
60
80
Magnitude(dB)
10
1
10
2
10
3
10
4
−200
−100
0
100
200
Phase(deg)
Frequency(Hz)
FIGURE 10.5
Open-loop frequency response with disturbance rejection at 4 and 8 kHz.
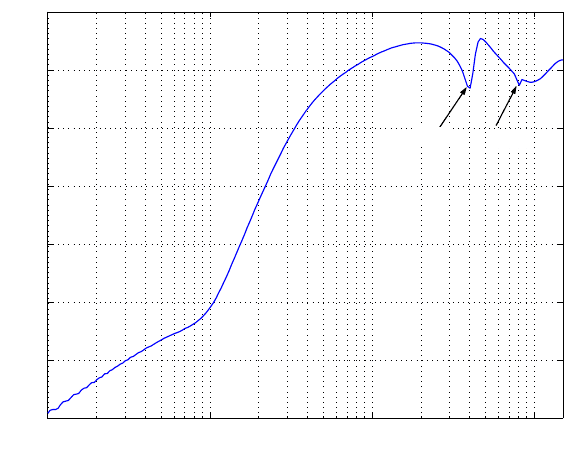
Blending Control for Multi-Frequency Disturba nce Rejection 209
10
1
10
2
10
3
10
4
−60
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
4 kHz
8 kHz
FIGURE 10.6
Simulated sensitivity function with disturbance rejection at 4 and 8 kHz.
Next, assume that dist urbances at three frequencies are to be rejected si multane-
ously, and the frequ encies are not t he plant resonance frequencies. The disturbances
are modeled as (10.37) with ω
1
= 2π3000, ξ
1
= 0.02, ζ
1
= 0.7, k
d1
= 40 for D
1
(s),
ω
2
= 2π6500, ξ
2
= 0.085, ζ
2
= 0.61, k
d2
= 50 for D
2
(s), and ω
3
= 2π10000,
ξ
3
= 0.3, ζ
3
= 0.6, k
d3
= 52 for D
3
(s).
The order o f the designed C(z) is 46. After order reduction, a 31st o rder C(z) is
obtained. With the lower order C(z), the compensated open-loop frequency response
is shown in Figure 10.8. The simulated and the measured sensitivity functions are
shown in Figure 10.9 where three rejection frequency bands around 3 kHz, 6.5 kHz,
and 10 kH z are clearly seen.
The rejection capabilities for these three disturbances are furt her examined via
more simulations. It is shown t hat changing rejecti on capability for 3 kHz distu r-
bance by adjusting k
d1
and/or ξ
1
will change that for 6.5 kHz, while will not affect
much on that for 10 kHz. The rejection change for 6.5 kHz disturbance by chang-
ing k
d2
, ξ
2
or ζ
2
will not lead to much change to other two disturbance rejections.
Changi ng parameters ξ
3
, ζ
3
and k
d3
of D
3
for 10 kHz disturbance will affect the
rejection f or the other two dist urbances more than itself.
210 Modeling and Control of Vibratio n in Mechanical Systems
10
1
10
2
10
3
10
4
−70
−60
−50
−40
−30
−20
−10
0
10
20
Frequency(Hz)
Magnitude(dB)
FIGURE 10.7
Measured (solid curve) sensitivity function with di sturbance rejection at 4 and 8 kHz.
10
1
10
2
10
3
10
4
−20
0
20
40
60
80
Magnitude(dB)
10
1
10
2
10
3
10
4
−200
−100
0
100
200
Phase(deg)
Frequency(Hz)
FIGURE 10.8
Open-loop with disturbance rejection at 3, 6.5, and 10 kHz.

Blending Control for Multi-Frequency Disturba nce Rejection 211
10
1
10
2
10
3
10
4
−60
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
FIGURE 10.9
Sensitivity function with disturbance rejection at 3, 6.5, and 10 kH z.
10.4.2 Rejecting a combined mid and hig h frequency disturbance
Previously, the f requencies of the disturbances th at need to be rejected are higher than
the bandwidth. In this section, we consider two d isturbances near the bandwidth:
one at 2 kHz, higher than the bandwidth, and the other at 650 Hz, lower than t he
bandwidth. The disturbance models are as in (10 .37) where ω
1
= 2 π650, ξ
1
= 0.05,
ζ
1
= 0.8, k
d1
= 7 7 for D
1
(s) at 650 Hz, and ω
2
= 2π2000, ξ
2
= 0.0046, ζ
2
= 0.85,
k
d2
= 0.1 for D
2
(s) at 2 kHz.
The resultant contr oller C(z) is of 27th order. By close zero-pole cancelations, a
21st order controller can be obtained, and is able to accompl ish th e task o f rejecting
D
1
and D
2
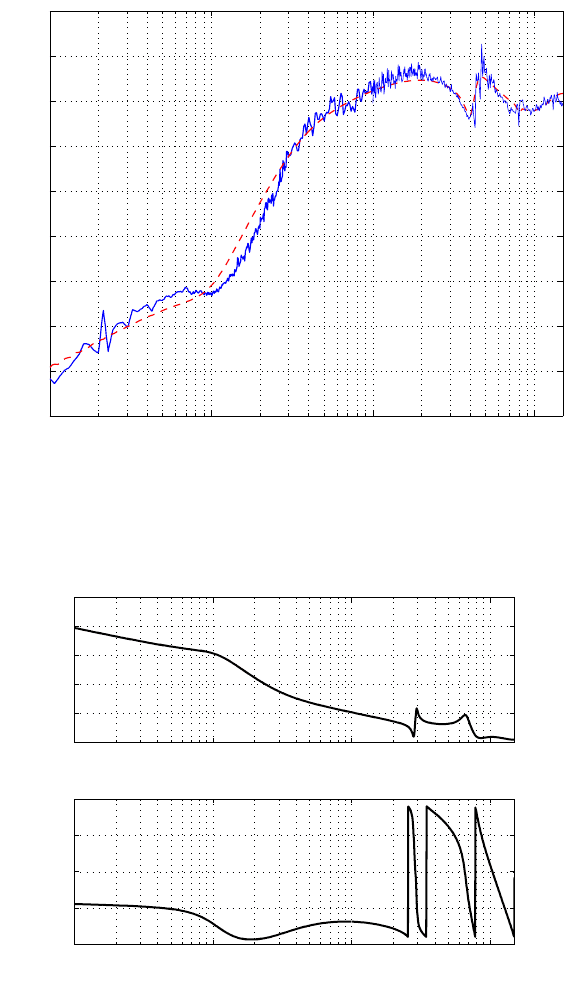
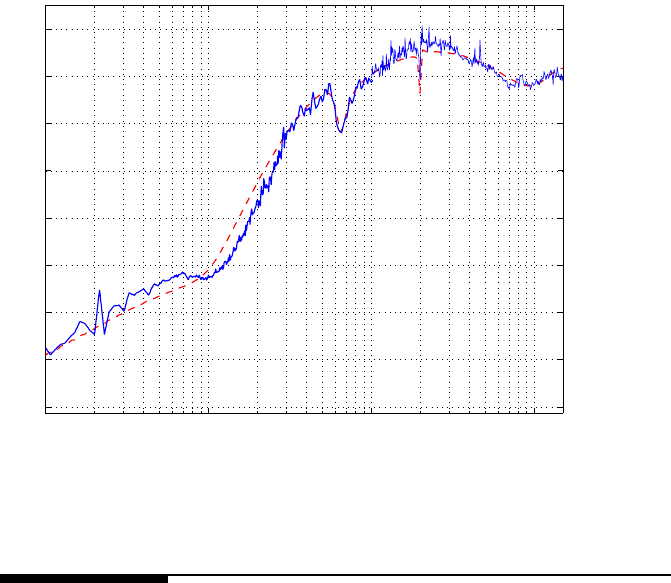
, which is illustrated in Figures 10.10 and 10.11. In Figure 10.10, a
significant point is that corresponding to the peaks at 650 Hz and 2 kHz, the phases
are both lifted, which is desired in order no t t o lose the phase margin.
As observed in Figure 10.11, |S(z)| < 0 at 2 kHz. The experimentally measured
|S(z)| is plotted; see the roug h curve in Figure 10.11. Addi tional simulations show
that decreasing damping ξ
1
will not only lower |S(z)| at 650 Hz, but also lower it
at 2 kHz. Increasing k
d1
will lower |S(z)| at 650 Hz, but will increase the hump of
S(z) and cause slight increase of |S(z)| at 2 kHz. On th e other hand, increasing k
d2
in D
2
(s) for 2 kHz disturbance will not affect much on |S(z)| at 65 0 Hz. Changing
ζ
2
will easily cause phase loss at 2 kHz. It is thus suggested to change k
d2
and ξ
2
to
have a satisfactory sensitivity functio n |S(z)| at 2 kHz without causing phase loss.
Using the method of phase lead peak filter in Chapter 8, the rejection capability
212 Modeling and Control of Vibratio n in Mechanical Systems
for vibrations at 650 Hz and 2 k Hz can be achieved with two peak filters, say pf
1
and pf
2
, which are individually designed to deal with the two vibration s, and then
the two filters are connected in parallel, i.e., 1 + pf
1
+ pf
2
. In this design method,
a baselin e controller needs to b e designed first, then the two peak filters are obtained
based on the pre-designed baseline contro ller. Thus the rejection performance of the
system for vibration in other frequency ranges depends on the pre-designed base-
line controller. Moreover, the phase lead peak filter method is difficult to deal with
multi-frequency vibrations in hig her frequency range and at frequencies near plant
resonance modes, that however have been treated in this chapter.
10
2
10
3
10
4
−20
0
20
40
60
Magnitude(dB)
10
2
10
3
10
4
−200
−100
0
100
200
Phase(deg)
Frequency(Hz)
FIGURE 10.10
Open-loop with distur bance rejectio ns at 0.6 5 and 2 kH z.
REMARK 10.1 From the above application results and a nalysis, it is
noted that to deal with lower (say ≤ 2 kHz) frequency disturbances, the pro-
posed control design method based on the blending technique works like the
phase lead peak filtering method. For higher (say > 2 kHz) frequency distur-
bances, it works like phase-stabilized control [86]. This feature is beneficial to
the stability of the closed-loop system.
Blending Control for Multi-Frequency Disturba nce Rejection 213
10
1
10
2
10
3
10
4
−70
−60
−50
−40
−30
−20
−10
0
10
Frequency(Hz)
Magnitude(dB)
FIGURE 10.11
Sensitivity function with disturbance rejections at 0.65 and 2 kHz.
10.5 Co nclusion
The rejectio n problem of several disturbances arou nd different frequencies has been
formulated as a control b lending problem. A controller for each disturbance rejec-
tion has been designed individually by using the H
2
optimal control metho d. The
ultimate controller has been obtained by blending all these H
2
controllers so that all
these d isturbances can be rejected simultaneously. The control blending method has
been respectively applied to design a controller for a 1.8-inch HDD VCM actuator
in three cases, (1) rejecting two disturbances of frequencies higher than bandwidth
and close to actuator resonance frequencies, (2) rejecting three disturbances with fre-
quencies higher than bandwidth and different f rom r esonance frequencies, and, (3)
rejecting on e disturbance with fr equency lower than bandwidth and another high er
than bandwidth. Simulatio n and experimental results have shown that the control
blending techniq ue results in a simultaneous attenuation for these disturbances. In
addition, it is worth noting that t he method is able to prevent phase loss when it is
used to deal with disturbances near the bandwidth.
