Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

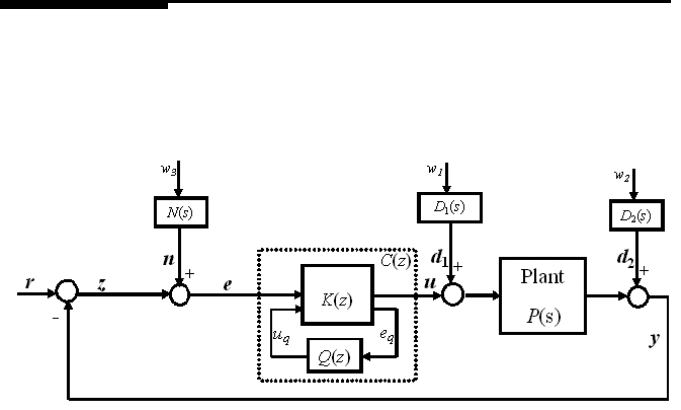
184 Modeling and Control of Vibratio n in Mechanical Systems

9.2 Problem formulation

FIGURE 9.1

control scheme with Q parametrization for controller design.

In the previou s chapter, speciﬁcations on sensitivity funct ion S(z) are described

|S(f

)| < r

, f

< f

, i = 1, 2, ···, m (9.1)

where r

< 1 is a positive scalar, and f

and f

deﬁne the f requency range.

Such an upper-bound speciﬁcation as in (9.1) will lead to a problem when the fre-

quency f

is larger than and especially n ear th e desired bandwidth or 0-dB crossover

frequency of S(z). The 0-dB crossover frequ ency of S(z) will be pushed away to-

wards a higher frequency, as seen in Figure 9.9, which tends to damage the system

stabil ity and det eriorate the system high-frequency perfor mance. In view of this, a

lower-bound speciﬁcation, i.e.,

|S(f

)| ≥ 1, f

≤ f

(9.2)

is required. This speciﬁcation helps to ﬁx the bandwidth or 0 -dB crossover frequency

of S(z), which will be seen later in the appl ication results.

The problem of the speciﬁc disturbance rejection can b e solved by imposing such

performance speciﬁcations in (9.1) and then using the KYP Lemma-based control

design method in Chapter 8. However, as shown in Figure 9.1 associated with Fig-

ure 8.14, th e servo mechanical system suffers from vari ous kinds of distur bances

and sensing noise. The KYP Lemma-based control design cannot include all dis-

turbances and noises which contribute to the position error. In view of this, we also

Combined H

and KYP Lemma-Based Control Design 185

take into account the overall perfor mance of the servo control system, which is repre-

sented as t he so- call ed track misregistration (TMR) induced by w =





passing through D

(s), D

(s), and N (s). I t is expressed by the standard deviation

of z, and

= σ

, (9.3)

when w is a white noise with zero mean and identity covariance matrix, where T

is the transfer function from w to z.

In the next section, we proceed to the controller design to achieve the speciﬁca-

tions in (9.1) and (9.2), and meanwhil e to optimize (9.3).

9.3 Controller design for speciﬁc disturbance rejection and over-

all error minimization

The generalized KYP Lemma-based design method in Chapter 8 is used to design a

controller for speciﬁc disturbance at tenuation.

Let (A

, B

, C

, D

) and (A

, B

, C

, D

) respectively be the state-space model

of plant P (z) and controller C(z). In order to convexify matri x inequalities, the

Youla parametrization approach with the Q(z) in a FIR ﬁlter form is app lied and the

controller structure is shown in Figure 9.1. K(z) is an observer based controller that

can be designed using the LQG method as in (8.11)−(8.12).

For the presentation of the KYP Lemma, we denote

σ(S, Π) :=





∗





(9.4)

where S(z) = S(e

jθ

), I stands for an identity matrix and Π a Hermiti an matrix of

the form

Π =



∗



, (9.5)

which speciﬁes the frequency domain property to be investigated.

9.3.1 Q parametrization to meet speciﬁc speciﬁcations

A. Speciﬁcation (9.1)

Recall from (8.13)−(8.14) that a set of sensitivity functions S(z): (

can be Q-parameterized.

According to the denotation (9.4)−(9.5), the speciﬁcation |S(z)| ≤ r is written as

σ(S, Π) ≤ 0 with

Π =



∗





1 0

0 − r



. (9.6)

186 Modeling and Control of Vibratio n in Mechanical Systems

Thus based on t he KYP Lemma in Chapter 8, achieving





jθ





≤ r for the

frequency range θ

≤ θ ≤ θ

can be obtained by solving the following matrix

inequality



I 0



∗



I 0





0 I



∗



0 I



≤ 0, (9.7)

which is, since Π

> 0, equivalent to







I 0



∗



I 0





0 0

0 −r







∗





−Π





≤ 0, (9.8)

where

Σ =



−U e

jθ

−jθ

V U −(2 cos θ

) V



, (9.9)

(θ

+ θ

)

, θ

(θ

−θ

)

, (9.10)

U and V are Hermiti an matrices and V ≥ 0.

To convexify the matrix inequality (9.8), we shall give a state space realization

of S(z) = T

(z) + T

(z) Q (z) T

(z). Denote the state-space representation

of T

(z) and T

(z)T

(z) by (A

t11

, B

t11

, C

t11

, D

t11

) and (A

, B

, C

, D

respectively. Then a state-space model of S(z) can be written as (8.17)−(8.18).

B. Speciﬁcation (9.2)

Again, accordin g to the denotation (9.4)−(9.5) th e speciﬁcation |S(z)| ≥ r is

equivalent to σ(S, Π) ≤ 0 with

Π =



∗





−1 0

0 r



. (9.11)

However, because Π

< 0, (9.7) can not be converted equivalently to (9.8), which

means (9.7) is not possibly convexiﬁed according to the method i n Section 9.3.1.

Hence we resort to the following speciﬁcation

σ (S, Π) = aR(S) + bI (S) + c, Π :=



0 a + jb

a − jb 2c



(9.12 )

where R and I denote the real and the imaginary parts o f S(e

jθ

). When a, b and

c are properly selected, |S(z)| ≥ r can be achieved. A simple selection is a = 0,

b = −1, c = r, and

σ (S, Π) = −I (S) + r. (9.13)

Thus σ(S, Π) ≤ 0 means I (S) ≥ r, and subsequently |S(z)| ≥ r. In this situation,

Π =



∗





0 −j

j 2r



, (9.14 )

Combined H

and KYP Lemma-Based Control Design 187

where Π

= 0 and (9.7) is equivalent to



I 0



∗



I 0





∗

+ Π

∗

D + Π



≤ 0, (9.15)

which is a linear matrix inequali ty with unknown variables in

C and

D only, and can

be solved usi ng the same method as in Section 9.3.1A.

It should be mentioned that R(S) ≥ r can also be used to achieve |S(z)| ≥ r, if

it is suitable for a speciﬁc application. In this case,

Π =



∗





0 −1

−1 2r



, (9.16 )

and the linear matrix i nequality (9.15) remains applicable.

9.3.2 Q parametrization to minimize H

performance

Next we focus on the design of Q(z) to minimize the H

norm kT

. From Fi gure

9.1 we have

−z = N (z) w

+ S (z) [P (z) D

(z) w

+ D

(z) w

−N (z) w

] . (9.17)

Denote a state-space realization of P (z)D

(z), D

(z) and N(z) by (A

, B

, C

, D

, B

, C

, D

), and (A

, B

, C

, D

), respectively. It follows from (8.13) and

(8.17)−(8.18) that

x (k + 1) =

Ax (k) +

Bw(k), (9.18)

−z (k) =

Cx (k) +

Dw(k), (9. 19)

where,

A =







0 0 0

0 A

0 0

0 0 A

−







B =







0 0

0 B

0 0 B

−







, (9. 20)

C =



−

+ C



D =



−

+ D



The H

norm kT

can be minimized as follows:

min

(Ξ=Ξ

>0, Ω=Ω

>0)

T race (Ω) (9.21)

subject to

A −Ξ +

C < 0 (9.22)

B +

D < Ω (9.23)

188 Modeling and Control of Vibratio n in Mechanical Systems

or equivalently,



A − Ξ

C −I



< 0 (9.24)



−Ω +

D −I



< 0 (9.2 5)

where

A =







0 0 0 0 0

0 A

0 0 0 0

0 0 A

0 0 0

t11

−B

t11

0 0

−B

0 A

C −B

0 B







B =







0 0

0 B

0 0 B

t11

−B

t11

−B







C =



t11

+ D

) C

t11

+ D

) C

t11

+ D

) C

t11



D =



t11

+ D

) D

t11

+ D

) D

−(D

t11

+ D

) D

+ D

] . (9.2 6)

Note that the Q(z) coefﬁcients q

(i = 0, 1, . . . , τ) only appear in C

and D

Therefore, from (8.17)−(8.18) and (9.26), we know that q

exists only in

and

D. In this case, (9.8), (9.15) and ( 9.24)−(9.25) deﬁne LMIs in terms of the

variables U, V , Ξ, Ω and q

. Hence, the Q(z) coefﬁcients q

can be computed via a

convex optimization.

With t he solved Q(z): (A

, B

, C

, D

), t he controller C(z) is then given by



−B

M + LC

+ B





L + B





−M + D



= D

(9.27 )

9.3.3 Design steps

To summarize, a design procedure for con troller C(z) is given as foll ows.

Combined H

and KYP Lemma-Based Control Design 189

Step 1. Design K(z) from (8.11)−(8.12).

Step 2. Compute T

(z), T

(z) and T

(z) from (8.14), and obtain the state space

model (

D) i n (8.17)−(8.18).

Step 3. Based on disturbance spectrum and bandwidth requirement, specify the

positive scalars r

and r

, and the frequency point s f

(i = 1, . . ., m) and f

(j = 1,

. . . , n) for the sensitivity function S(z), i.e.,

|S (f

)| < r

, f

≤ f

, (9. 28)

and

|S (f

)| > r

, f

≤ f

. (9.29 )

For each speciﬁcation, const ruct the LMIs (9.8) and (9.15) in terms of the variables

U, V , C

and D

Step 4. Construct the LMIs (9.24)−(9.25) in terms of the variables Ξ, Ω, C

and

Step 5. Obtain Q(z) : (A

, B

, C

, D

) by solving the above LMIs using the

MATLAB LMI to olbox.

Step 6. Obtain the controller C(z) from (9.27).

9.4 Simulation and implementation result s

This section will apply the control design method in Section 9.3 f or a PZT microac-

tuator to separately reject one or two speciﬁc disturbances and meanwhile minimize

the H

norm of the PES.

9.4.1 System models

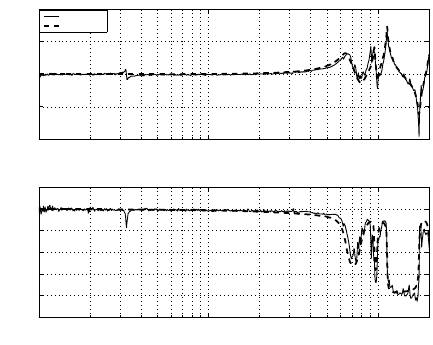
The frequency response of the PZT microactuator, shown in Figure 9.2, was obtained

using a LDV and a DSA. The main resonance modes of the plant are at frequencies

6.5 kHz, 9.5 kHz, 11.3 kHz, and 20 kHz. The identiﬁed pl ant model of th e micro-

actuator P (s) has the following parameters:

Zer os = 10

× [−0.0296 ± 0 .4927j, − 0.0110 ± 1.0964j,

− 0.7116 ± 0.6275 j, − 0.0093 ±0.6198j, 0.8168],

P oles = 10

×[−0.0255 ±1.2733j, − 0.0050 ± 0.7100j,

− 0.0048 ± 0.5981 j, − 0.0245 ±0.4071j, − 0.8168],

Gain = −0.4819.

The frequency response of the plant model is plotted against the measured data in

Figur e 9.2 for comparison and it is subsequently discretized in MATLAB using the

“zoh” method with a sampling rate of 40 kHz.

190 Modeling and Control of Vibratio n in Mechanical Systems

−40

−20

Frequency (Hz)

Magnitude (dB)

−250

−200

−150

−100

−50

Frequency (Hz)

Phase (deg)

Measured

Modeled

FIGURE 9.2

Frequency response of a PZT microactuator.

9.4.2 Rejection of speciﬁc disturbance and H

performance minimiza-

tion

Consider the disturbances in Figure 8.14; the disturbance around 650 Hz is due to

the disk vibration. A suitable feedback controller, C(z) has to be designed for the

system so th at the overall system is stable and the disturbance around 650 Hz is

suppressed su fﬁciently, while ensuring that the H

norm of the position error signal

is minimized. Hence, the desired speciﬁcation of the sensitivity functi on S(z) is

|S ( f)| < −10 dB for 610 Hz ≤ f ≤ 670 Hz and at the same time the position error

signal is to be minimized.

The parameters of a ﬁr st-order FIR Q(z) are obtained b y solving the three LMIs

(9.8), (9.24) and (9.25). For comparison, another controller is designed without H

minimization and just to suppress the vibration around 650 Hz. With each of the

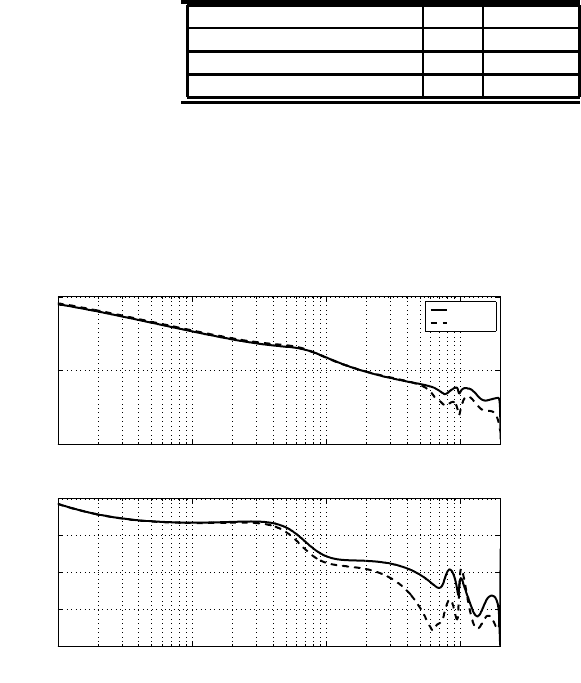
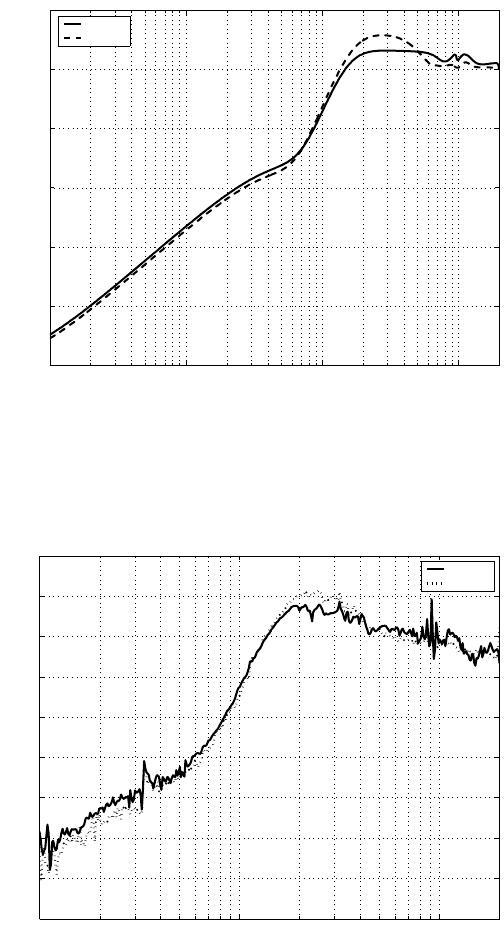
two designed controllers, the frequ ency response of the open-loop C(z) ×P (z) and

the sensitivity function S(z) are depicted in Figure 9.3 and Figure 9.4. It is seen

that the hump of S(z) is reduced to about 3 dB with the controller designed by

the combined method, i.e., the combined H

optimization and speciﬁc disturbance

rejection method. On the other hand, the performance sp eciﬁcations listed in Table

9.1 show that the proposed method offers better stabilit y margins although the open-

loop crossover frequency is a bit lower.

Experiments are carried out for the KYP Lemma-based controller and the KYP+H

controller to verify the simulation results. The controllers are implemented using

dSPACE 1103 on a TMS320C240 DSP board and the st ructure of the experimental

setup is the same as in Figure 8.10. The sensitivity function of the system is obtained

by the rati o of the measurements in Channel 2 and Channel 1 o f the DSA, where a

swept sine signal is the reference input. The sensitivity f unction obtained from the

Combined H

and KYP Lemma-Based Control Design 191

TABLE 9.1

Comparison of performance speciﬁcations

Method KYP KYP+H

Crossover frequency (kHz) 1.85 1.78

Gain margi n (dB) 7.9 1 2.6

Phase margin (deg) 35.4 45.9

experiment, as shown i n Figure 9.5, demonstrates th e effectiveness of the proposed

method. As a result, as seen in Figure 9.6, the position error is reduced and its σ

value has a 4% improvement .

−50

Magnitude(dB)

−250

−200

−150

−100

−50

Phase(deg)

Frequency(Hz)

KYP+H

KYP

Frequency(Hz)

FIGURE 9.3

Open-loop frequency responses.

192 Modeling and Control of Vibratio n in Mechanical Systems

−50

−40

−30

−20

−10

Magnitude(dB)

Frequency(Hz)

KYP+H

KYP

FIGURE 9.4

Designed sensitivity functions.

−35

−30

−25

−20

−15

−10

−5

Frequency (Hz)

Magnitude (dB)

KYP+H

KYP

FIGURE 9.5

Comparison of sensitivity functions obtained from experiment.

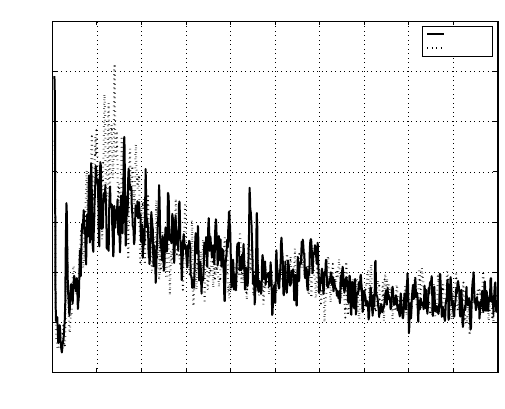
Combined H

and KYP Lemma-Based Con trol Desig n 193

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

x 10

0.05

0.10

0.15

0.20

0.25

0.30

0.35

Frequency (Hz)

NRRO magnitude (nm)

KYP+H

KYP

FIGURE 9.6

NRRO power spectrum with KYP Lemma-based controller with and without H

minimization.

9.4.3 Rejection of two disturbances wi th H

performance minimiza-

tion

In what follows, we include one more speciﬁc disturbance rejection at 2 kHz (see

Figure 9.7), which is caused by air ﬂow and is near the desired servo bandwidth 1

kHz. In this case, the speciﬁcations on S(z) are set as:

i. |S (f)| < −10 dB for 610 Hz ≤ f ≤ 670 Hz;

ii. |S (f)| < −5 dB for 1950 Hz ≤ f ≤ 2050 Hz;

iii. |S (f)| > 0 dB for 990 Hz ≤ f ≤ 1010 Hz,

where in addition to the rejection of disturbance at 650 Hz, the disturbance around

2 kHz i s also to be suppr essed. Note that the third speciﬁcation aims to ﬁx the

bandwid th.

By solving the LMIs (9.8), (9.15) and (9.24)−(9.25) in terms of the variables

P , V , Ξ, Ω, C

and D

, a con trol ler C(z) which leads to the S(z) satisfying the

speciﬁcations can be obtained with a fou rth-o rder FIR Q (z). With the result ant

controller, t he open-loop frequency response and the sensitivity function are shown

in Fi gures 9.8 and 9.9, where the speciﬁcations (i), (ii) and (iii) have been achieved

and the closed-loop system remains stable. The open-loop gain and phase margins

are 14.6 dB and 49.5 degrees, respectively.

We have also carried out experiments to verify the designed controller. The ex-

perimental result s of the open-loop frequency response and sensitivity function are