Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

164 Modeling and Control of Vibratio n in Mechanical Systems

LEMMA 8.1

[62] Consider the sensitivity function S(z) =

C(zI −

−1

B +

D with

A being

stable. Then, for a given scalar r > 0, | S(e

jθ

)| ≤ r over a ﬁnite frequency

range if and only if there exist Hermi tian matrices U and V ≥ 0 such that







I 0



∗



I 0





0 0

0 −r







∗





−I





≤ 0, (8.7)

where

(i) for low frequency range |θ| ≤ θ

Σ =



−U V

V U − (2cosθ



; (8.8)

(ii) for middle frequency range θ

≤ θ ≤ θ

Σ =



−U e

jθ

−jθ

V U −(2cosθ



= (θ

+ θ

)/2, θ

= (θ

−θ

)/2; (8.9)

(iii) for high frequency range |θ| ≥ θ

Σ =



−U −V

−V U + (2cosθ



. (8.10 )

For a given contro ller C(z), t he above gives a necessary and sufﬁcient condition

for evaluating if |S(z)| ≤ r over so me given frequency range in terms of LMI.

However, (8.7) is no longer an LMI when the controller C(z) = (A

, B

, C

, D

)

is to be design ed since

A and

B involve the unknown parameters A

, B

, C

and

. Further, it is not possible to be converted to an LMI by Schur complement since

the matrix Σ is not deﬁnite. To overcome this difﬁculty, in the following we apply a

Youla parametrization approach where the controller C(z) is now of the structure as

shown in Figure 8.1.

Let K(z) be a given observer based controller that can be designed using ap-

proaches such as the LQG contro l:

ˆx(k + 1) = A

ˆx(k) + B

u(k) + L(z(k) + C

ˆx(k)), (8.11)

u(k) = −M ˆx(k ). (8.12 )

Then, as stated in Chapter 5, the set of sensitivity functions can be parameterized as

S(z) = T

(z) + T

(z)Q(z)T

(z) (8.13)

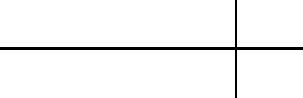
Generalized KYP Lemma-Based Loop Shaping Control Design 165

where Q(z) is a st able transfer functio n to be designed and



(z) T

(z)

(z) 0



= C

(zI − A

)

−1

+ D











−B

0 B

−LC

− B

M + LC

L B

−C

M 1 −D

−C

1 0







. (8.14)

If Q(z) has the state-space realization (A

, B

, C

, D

), then the designed con-

troller C(z) is given by



−B

M + LC

+ B



, (8.15)



L + B



, C



−M + D



= D

. (8.16 )

Denote the state space representatio ns of T

(z) and T

(z)T

(z) by (A

t11

, B

t11

, D

t11

) and (A

, B

, C

, D

), respectively, then from (8.13) a state space model

of S(z) can be written as

A =





t11

0 0

0 A

0 B





B =





t11





, (8.17 )

C =



t11



D = D

t11

+ D

. (8.18)

Let Q(z) be an FIR ﬁlter:

Q(z) = q

+ q

−1

+ q

−2

+ ... + q

−τ

, (8.19)

q = [q

, ... , q

] (8.20 )

which is to b e designed so that the required bounded realness of the sensitivity func-

tion is satisﬁed. It is known that a state space realization for Q(z) can be given



0 I

τ−1

0 0



, B



(τ−1)×1



= [q

τ−1

··· q

] , D

= q

where I

τ−1

is the identity matrix o f dimensio n (τ −1) ×(τ −1) and 0

(τ−1)×1

is the

zero matrix of dimension (τ −1) ×1. Note that the ﬁlter parameter q to be designed

only app ears in C

and D

. Therefore, from (8.17)−(8.18), we know that q exists

C and

D only. In this case, (8.7) deﬁnes an LMI in terms of t he variables U,

V , and q. Hence, U, V , and the design parameter q can be computed via a convex

optimization.

166 Modeling and Control of Vibratio n in Mechanical Systems

The KYP Lemma-based control design can be carried out f ollowing the steps:

Procedure 8.1

Step 1. Compute M and L using MATLAB commands M = dlqr(A

, B

, C

R) and L = A

· d lqe(A

, B

, − C

, W

), where R is the weighting for the

control input in the cost function

J =

(ˆx

ˆx + u

Ru)

for linear quadratic r egulator design, and W

and W

are the variance matrices of

process noise and measurement noise for the Kalman estimator design. Here in

the KYP Lemma-based control design, R, W

, and W

can be chosen as identity

matrices.

Step 2. Compute T

(z), T

(z) and T

(z) from (8.14).

Step 3. Obtain the state space model (

D) in (8.17)−(8.18).

Step 4. Based on disturbance spectrum, specify the positive scalars r

and fre-

quency points f

(i = 1, ..., N ) for the sensitivity function

|S(f

)| < r

, f

≤ f

(8.21 )

where f

and f

deﬁne the f requency range. For each sp eciﬁcation on the resultant

sensitivit y function in the frequency range, construct the LMI (8.7) in terms of the

variables U , V , and q with r = r

Step 5. Obtain q, U and V by solving these LMIs using MATLAB LMI toolbox.

If the LMIs are not solvable, the speciﬁcations given i n Step 4 are to be adjusted.

Step 6. Obtain the controller parameters from (8.15)−(8.16).

8.4 Peak ﬁlter

Many other control methods are available to reject narrowband disturbance, such as

linear time invariant feedback methods using classical design and modern fr equ ency

shaping and ﬁlt er shaping, and adaptive feedforward methods using higher harmonic

control and LMS algorithm [57]. It h as been shown that most of these methods would

result in a compensator with light ly damped complex poles at the center frequency

of the disturbance. Such a compensator has high gains at speciﬁc frequency. It is

named as peak ﬁlter according to its shape of frequency response. The peak ﬁlter

F (s) works in the control loop as in Fig ure 8.2 with its discretized for m F (z).

8.4.1 Conventional peak ﬁlter

Conventionally, the peak ﬁlter is described as t he following model

F (s) =

+ 2ξ

s + ω

+ 2ξ

s + ω

, (8.22)

Generalized KYP Lemma-Based Loop Shaping Control Design 167

FIGURE 8.2

Peak ﬁlter F in the n ominal feedback loop.

FIGURE 8.3

Peak ﬁlter in the frequency domain.

168 Modeling and Control of Vibratio n in Mechanical Systems

where ω

= 2πf

is the center frequency in radian/sec and ξ

and ξ

are the damping

ratios with ξ

> ξ

. The peak ﬁlter F (s) can be designed according to its Bode plot,

as illustrated in Figure 8.3. M and N denote the peak height, ∆ stands for the peak

width corresponding to N. Let

m = 10

M/20

, n = 10

N/20

. (8.23)

When M ≫ N , ξ

and ξ

are determined approximately b y

∆

+ 2∆

2∆ + 2

√

n − 1, (8.24 )

. (8.25 )

The maximum phase loss θ caused b y the pair of the lightly damped complex poles

is given b y

θ = arctan

m −1

√

. (8.26 )

It is noticed that the conventional version of the p eak ﬁlter induces additional

phase loss. The phase loss negatively impacts the phase margin and distorts the

gain of the sensitivity fun ction around the disturbance frequency, particularly for

the disturbance near the 0 dB crossover frequency. To overcome t he drawback, a

phase-lead peak ﬁlt er [ 118] was proposed.

8.4.2 Phas e lead peak ﬁlter

The phase ﬁlter is improved by adding a differentiator to provide addition al phase

lead such that the phase margin is preserved and the sensitivity function curve is

smoothly shaped.

Let

(s) =

P (s)C(s)

1 + P (s)C(s)

. (8.27)

The peak ﬁlter adopts the following form

F (s) = K

−sin(φ)s

+ ω

cos(φ)s

+ 2ξω

s + ω

, (8.28)

where ω

is the disturbance frequency at which high disturbance rejection is required,

ξ ∈ (0, 1) is the damping ratio, φ is the phase angle determined by

φ = arg[T

(jω

)] ∈ [ −π, π], (8.29)

and 0 < K < γ is the positive ﬁlter gain. Let

G(ω, K) = 1 + T

(jω)F (jω), (8.30)

Generalized KYP Lemma-Based Loop Shaping Control Design 169

and γ is the minimal positive real solution of the following two equations:

Re[G(ω, γ)] = 0, (8.31 )

Im[G(ω, γ)] = 0. (8.32 )

An estimate of ξ and K in the ﬁlter (8 .28) is given by

ξ =

∆

(ω

+ 0.5∆

)

4ω

, (8.33 )

K = (10

M/20

− 1)

2ξ

(jω

)

, (8.34)

where the disturbance bandwi dth ∆

is deﬁned as the frequency difference between

the two p oints whose magnitudes are 1/

√

2 times of the peak value, and M in unit

dB is the desired reduction rati o of the narrowband disturbance.

The disturbance ﬁlter in (8.28) is a general high-gain controller to reject narrow-

band disturbances in a speciﬁc frequency range because the ﬁlter zero lo cati on can

be automatically shifted according to the disturbance frequency associated with the

baseline servo syst em with C(s) and P (s).

8.4.3 Group peak ﬁlter

The group ﬁltering scheme is used to compensate multiple frequency narrowband

disturbance. A parallel structure of the group peak ﬁlter is described as

F (s) =

i=1

(s), (8.35 )

where the sub-ﬁlter F

(s) is given by (8.28) with the corresponding ﬁlter parameters

(ω

, φ

, ξ

, K

An illust ration example is shown in Figure 8.4 with t he sensitivity functions plot-

ted before and after activating the group ﬁlter w ith two sub-ﬁlters at ω

= 2π700

and ω

= 2π2000. The ﬁlters associated with so lid and dashed curves have different

parameters.

8.5 Application in h igh frequency vibration rejection

In this section, we shall provide an example to demonstrate the design and effective-

ness of the pr oposed KY P based contro l to r eject narrowband disturbances at high

frequencies. The previously intr oduced peak ﬁlt ering method ﬁnds it difﬁcult to deal

with dist urbances in high frequency range, especially near the actuator resonance

modes.

170 Modeling and Control of Vibratio n in Mechanical Systems

−35

−30

−25

−20

−15

−10

−5

Frequency (Hz)

Magnitude (dB)

with filter

without filter

FIGURE 8.4

Sensitivity functions before and after grou p peak ﬁlteri ng activated.

FIGURE 8.5

PZT microactuator attached to VCM actuator arm.

Generalized KYP Lemma-Based Loop Shaping Control Design 171

0 2000 4000 6000 8000 10000 12000

0.5

1.5

2.5

x 10

−3

Frequency(Hz)

PES NRRO power sepctrum(µm)

8 kHz

10 kHz

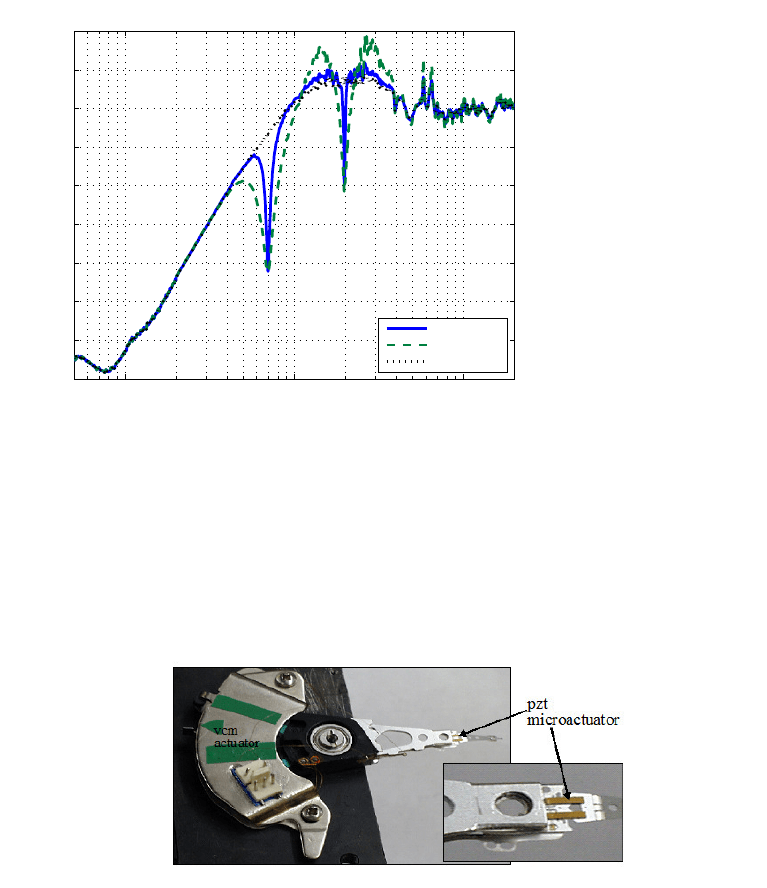
FIGURE 8.6

Power spectrum of the position error befor e servo control.

A. System models

Figur e 8.5 shows one k ind o f microactuators for HDDs, which is a PZT actuated

suspension attached to a VCM actuator arm. Fig ure 8.6 shows an example of the

main disturbances that exist in the hard disk drive servo system. Besides the distur-

bances of low frequencies, the system suffers from the high f requency disturbances

around 8 kHz and 10 kH z, which are induced by air turbulence to suspensions or

sliders in HDDs. For higher rotatio nal speed HDDs, these dist urbances appear mor e

promin ent and create a signiﬁcant impact on the positioning accuracy of the R/W

head. Here we emplo y the generalized KYP Lemma to design a feedback control

C(z) for the microactuator such that the sensitivity function S(z) satisﬁes the re-

quired speciﬁcations so as to reject disturbances around 8 kHz and 10 kHz. The

desired speciﬁcations for the sensitivity function S(z) are set as

Spec.(a) |S(f )| < 0 dB, f ≤ 2 kHz,

Spec.(b) |S(f )| < −0.35 dB, 9950 Hz ≤ f ≤ 10050 Hz,

Spec.(c) |S(f )| < −1.41 dB, 7950 Hz ≤ f ≤ 8050 Hz.

Spec. (a) means to guarantee a 2 kHz b and w idth at least.

The transfer function of the PZT microactuator is given by

P zt(s) =

180828605599509(s

+ 3079s + 1.934 × 10

)

(s + 1.257 × 10

)(s

+ 791.7s + 1.567 × 10

)(s

+ 5089s + 7.195 × 10

)

(8.36 )

172 Modeling and Control of Vibratio n in Mechanical Systems

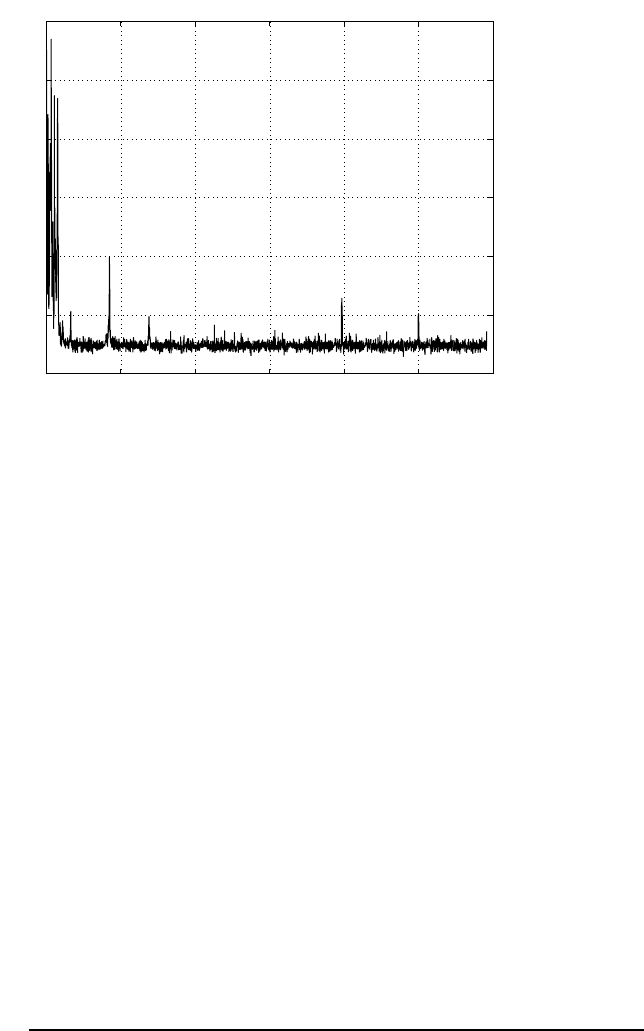
which is ob tained by curve-ﬁtting to its frequency response measured via DSA. A

comparison between the measured and the modeled frequency responses is shown i n

Figur e 8.7, where it is noticed that there are two dominant resonance modes at 6.3

kHz and 13. 5 kHz. P zt(s) is discretized using the zero-ord er-hold method to obtain

P zt(z). The sampling frequency being used is 4 0 kHz.

−40

−30

−20

−10

Magnitude(dB)

measured

modeled

−300

−200

−100

100

200

Phase(deg)

Frequency(Hz)

FIGURE 8.7

PZT micro actuator f requency response.

B. Controller design and LDV based experiment results

The plant P zt (s) is pr e-compensated by the integrator:

Int(z) =

6.3z

z − 1

, (8.37)

and two notch ﬁlters for suppressing the two main resonances at 6.3 kHz and 13.5

kHz before the KYP Lemma approach is applied to design a controller so that the

speciﬁcations (a), (b) and (c) can be satisﬁed. The notch ﬁlter is design ed as the

following form:

Notch =

+ 2ξ

s + ω

+ 2ξ

s + ω

, (8.38)

where ω

is the frequency of the resonance to be suppressed , ξ

< ξ

, and ω

and

shoul d be chosen to be close to each other so that the resultant notch ﬁl ter will

Generalized KYP Lemma-Based Loop Shaping Control Design 173

not inﬂuence the system stability. Here for the model (8.36) the notch ﬁlters after

discretization are as follows.

Notch1 (z) =

1.177z

−1.279z + 1 .154

−0.8751z + 0.9259

Notch2 (z) =

0.4011z

+ 0.3972z + 0.3532

+ 0.1391z + 0.007 922

, B

, C

, D

) in (8.3)−(8.4) is a state space descrip tion of the combined

system P (z) = Int(z) · Notch1(z) · N otch2(z) · P zt(z). Q(z) is chosen as the

-order FIR ﬁlter (8.19), and q

and q

are to be solved via the KYP Lemma.

As mentioned previously in Step 1 of the control design procedure, M and L are

obtained using MATLAB commands, i.e. M = dlqr(A, B

, C

, R) and L =

A · dlqe(A, B

, C

, W

Next we use the KYP Lemma to search for the coefﬁcients of Q (z). Three LMIs of

the f orm (8 .7) with Σ in (8.8) and (8.9) need to be solved in order to achieve Spec. (a),

(b) and ( c), respectively. The obtained q

and q

are q

= −0.4117, q

= 0.6371.

As such, C(z) can be obtained via (8.15)−(8.16). The resulting controller for the

PZT microactuator is C(z) · Int(z) · N otch1(z) · N otch2(z), and the sensitivity

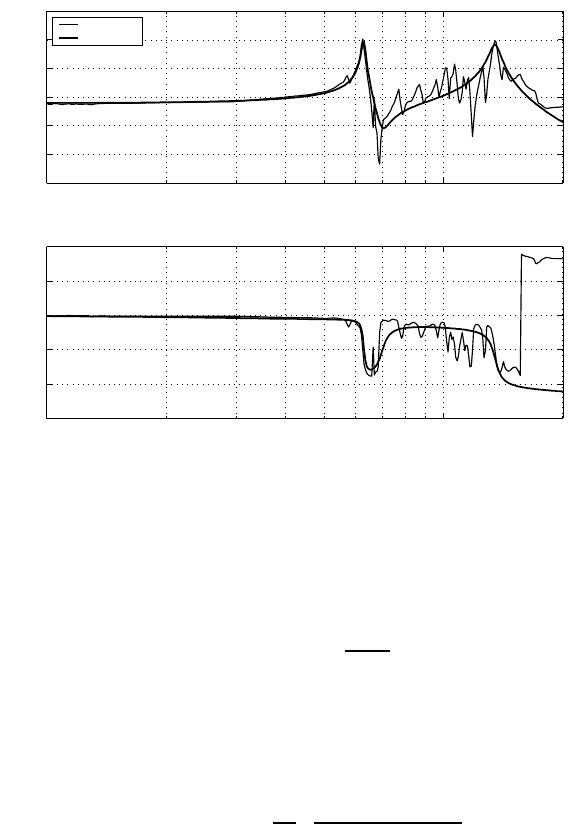
function i s sh own in Figure 8.8. It can be observed in Figure 8.8 that wi th Q(z), the

sensitivit y function is less than −4 dB and −2 dB at 8 kHz and 10 kHz respectively,

which means that speciﬁcations (a)−(c) have been satisﬁed by the searched Q(z).

The sensitivity function before the KYP Lemma based design is al so shown in Fig ure

8.8 where it can be seen that the required speciﬁcations are not met. Moreover,

as seen from Figure 8.9, the gain margin and the phase margin are 12 dB and 67

deg, higher than 7.7 dB and 63 deg before the KYP design. Observed from Fi gures

8.8 and 8.9, the KYP design increases the loop gain around 9 kHz, which results

in the reduction of the sensitivity function from 8 to 10 kHz. The price for this

compensation is a bit lower loop gain at lower frequencies, which is consistent with

the Bode Integral constraint for sensitivity function.

In the experiment, the dSpace 1103 on TMS320C240 DSP board was used to im-

plement the controller, and an LDV was used to measure the actuator displacement,

as shown in Figure 8.10. Channel 2 over Channel 1 of DSA is the measured fre-

quency response of the sensitivity f unction with a swept sin e signal as the reference.

Figur e 8.11 shows the experimental sensitivity functions, which agree with the sim-

ulation results in Figure 8.8. From (8.1), the σ values o f the position errors before

and after the KYP Lemma-based control versus frequencies are obtained and shown

in Figure 8.12. It can be seen that the performance with the KYP Lemma-based con-

trol is much better from 5 kHz onwards, and slightly worse before 5 k Hz, w hich is

consistent with the sensitivity functi ons in Figure 8.8.