Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

144 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 7.10

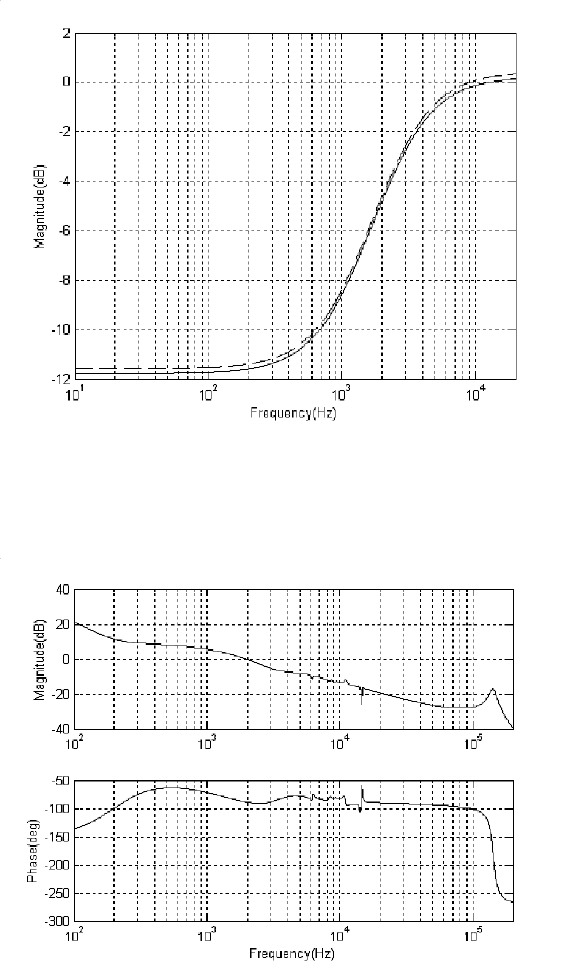
Sensitivity function S

(s) (sol id) and its weighting f unction inverse (dashed).

FIGURE 7.11

Open loop frequency response of the dual-stage system.

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 145

FIGURE 7.12

Sensitivity and complementary sensitivity functions.

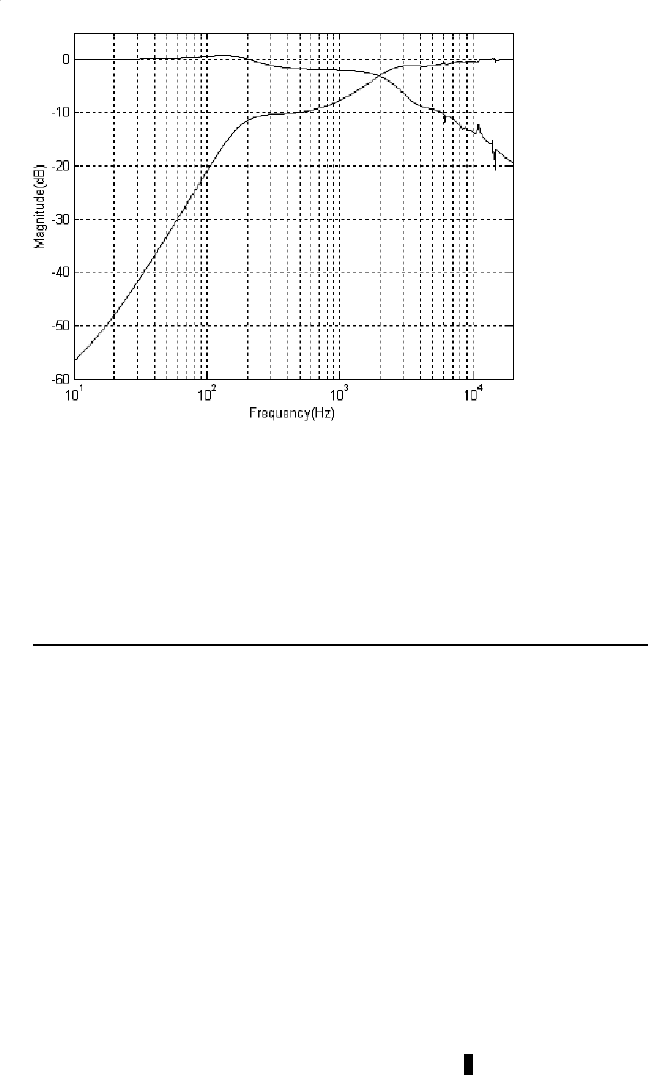
Case 2 : Poles are located around 10 kHz, such as the active piezoelectric suspen-

sion modeled by

(s) =

−1.438572836 × 10

(s − 6.157 ×10

)(s

+ 923.7s + 1.934 × 10

)

(s + 6 .157 ×10

)(s

+ 791.7s + 1.517 × 10

)(s

+ 5089s + 7.195 ×10

)

(7.14 )

with the fr equ ency response in Figu re 7.13 .

For the control design of (7.14), ε is kept unchanged to have th e same l ow-

frequency level of the sensitivity function as in Case 1, and ω is adjusted to be

2π210 7 to have a similar open-loop bandwidth. The resultant C

(s) is shown in

Figur e 7.14. The designed S

(s) and S

(s) are matched as in Figure 7.5, which

subsequently leads to the overall sensitivity as in Figure 7.16. We can observe that

a “ﬂat” sensitivi ty function has been achieved. The frequency response of the open

loop dual-stage system is shown in Figure 7.15, where th e gain margin is 31 dB and

the phase margin is 88

◦

. Note that a non-minimum phase zero i s included in the

microactuator model and a nearly “ﬂat” sensitivity function is still achieved.

REMARK 7.1 The control design is based on the relevant sensitivity

function only and does not consider robustness to plant pole/zero variations.

This will, however, not hamper the practical usability of the resulting con-

trollers due to the large gain and phase margins.

146 Modeling and Control of Vibratio n in Mechanical Systems

TABLE 7.1

Control performance comparison.

Microactuator model type Case 1 C ase 2

Gain Margin (dB ) 17 31

Phase Margin (deg) 90 88

Sensitivity function Flat Flat

Control perfor mances are summarized in Table 7.1 for the t w o dual-stage systems

consisting of different microactuators. It can be seen that they both achieve a “ﬂat”

sensitivit y fun ction with bandwidth of 2 kHz. Case 2, the PZT actuated suspension,

looks better th an Case 1, the MEMS actuator, in the sense that its gain margin is much

higher and phase margin is slightly lower, whereas its behavior is to be improved to

possess a characteristic as simple as a pade-delay which relies on i ts manufacturing

process. Also, from a manufacturing point of view, the MEMS actuator beneﬁts from

its mass production and low cost.

FIGURE 7.13

Microactuator frequency response.

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 147

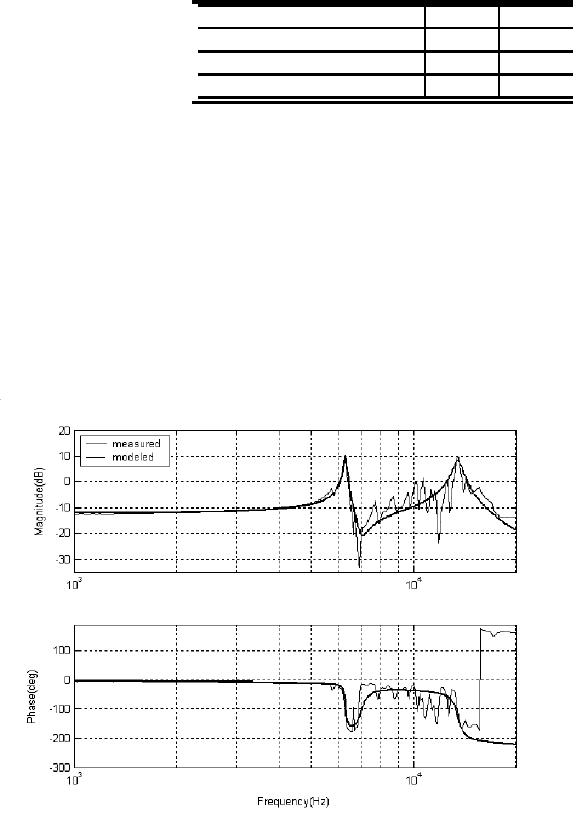
FIGURE 7.14

Frequency response of microactuator controller C

(s).

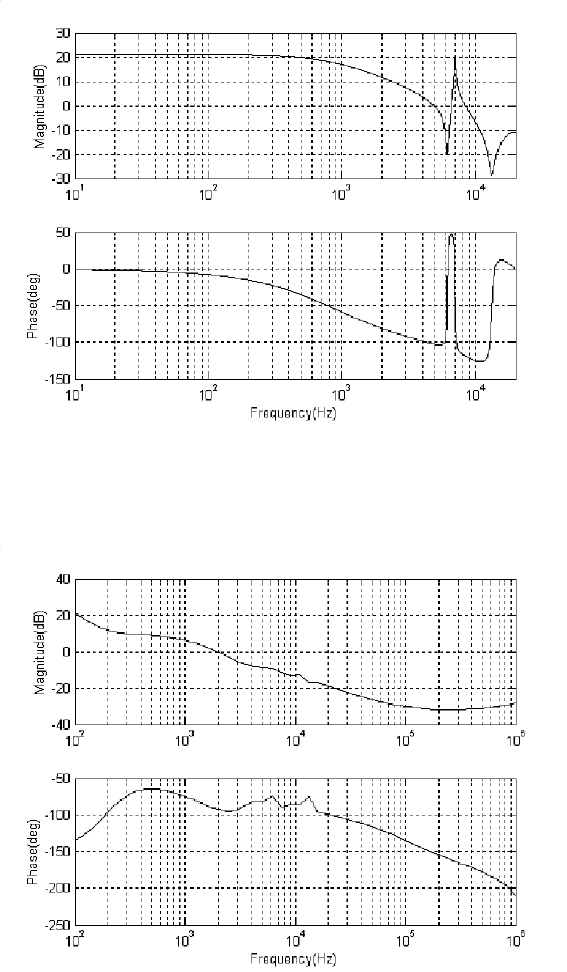
FIGURE 7.15

Open loop frequency response of the dual-stage system.

148 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 7.16

Sensitivity and complementary sensitivity functions.

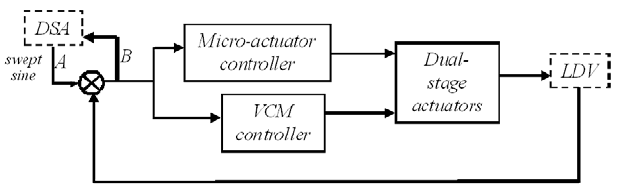
7.3.3 Implementation on a hard disk drive

The implementation is carried out for Case 2 in th e previous section, i.e., the dual-

stage system consisting of the VCM in Figur e 7.7 and the PZT microactuator in

Figur e 7.13. The VCM and PZT controllers are obtained by discretizing the designed

controllers with frequency responses shown in Figure 7.8 and 7 .14 and sampling rate

of 40 kHz.

The cont rollers are implemented with dSpace 1103 on TMS320C240 DSP board.

An LDV is used to measure the p osition of the dual-stage actuator as the feedback

signal. The displacement range used is 2 µm/V. A DSA is used to measure the

frequency response o f the sensitivit y function by i njecting a swept sine signal at

point A in Figu re 7.17. The frequency response of po ints B over A is th e sensitivity

function.

The resultant sensitivi ty functio ns are shown in Figure 7.18, where the roug h line

is the t ested result and the smooth line is the simulation result. We can observe that

the hump of the sensitivity function is lower than 3 dB, which is better than that with

the following PID-like controllers designed by the lead-l ag method:

(z) =

0.9z

− 1.778z + 0.8788

−1.532z + 0 .5326

, (7. 15)

(z) =

0.4081z + 0.2627

−1.209z + 0 .2631

. (7.16)

The tested and simulation results of the dual-stage open loop are shown in Figure

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 149

7.19. The step response of the dual-stage system is shown in Figur e 7.20, where

Channel 1 is the output corresponding to the reference Channel 4, C hannel 2 is the

control sig nal of VCM and Channel 3 is the control signal of PZT.

Note that the hump of the sensit ivity function S(z) is tested to be 3 dB, instead of

0 dB as in Figure 7.16. This is mainly due to the locations of the microactuator poles

which are around 10 kHz and n ot sufﬁciently far away from the bandwidth of 2 kHz.

We know that a pole at 20 kHz may not affect 2 kHz bandwidth that much and thus

it is not needed to include a pol e far beyond 20 kHz in th e actuator modeling for 2

kHz servo bandwidth. Moreover, an actuator with high-frequency poles is helpful to

the low-hump sensitivity function design. It is expected that the microactuator could

be modeled as a pade-delay within the frequency r ange of our interest. In the next

section we discuss the possibility of achievin g low-hump sensit ivity functions in the

discrete time domain.

According to ( 7.1), the sensitivity functio n as in Figure 7.18 must amplify the cor-

responding high-frequency disturbances due to the hump above 0 dB, and certainly

the one with t he lower hump will result in less ampliﬁcation.

The posi tion error is evaluated according to (7.1) wi th the sensitivity function in

Figur e 7.18 associated with the PES spectrum in Figure 7.2. The Parseval’s formula

stated in Chapter 1 addresses how to calculate σ value in t he frequency domain. As

such, Figure 7.21 shows the 3σ value of position error versus frequencies. The low-

hump design outperfo rms the PID design for disturbance rejection with almost the

same performance at frequencies lower than 1.5 kHz, which is consistent with Figure

7.18.

FIGURE 7.17

Experimental structure.

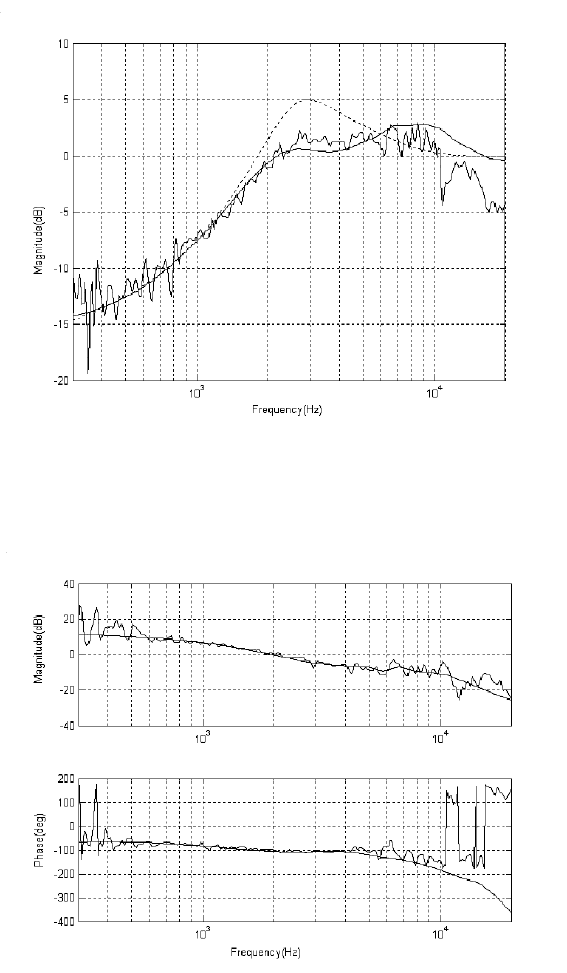
150 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 7.18

Sensitivity function of the dual-st age system (smooth line: simulation result; rough

line: testing result; dotted l ine: PID design).

FIGURE 7.19

Open loop frequency r esponse of the dual-stage system (smooth line: simulation

result; rough line: testing result.)

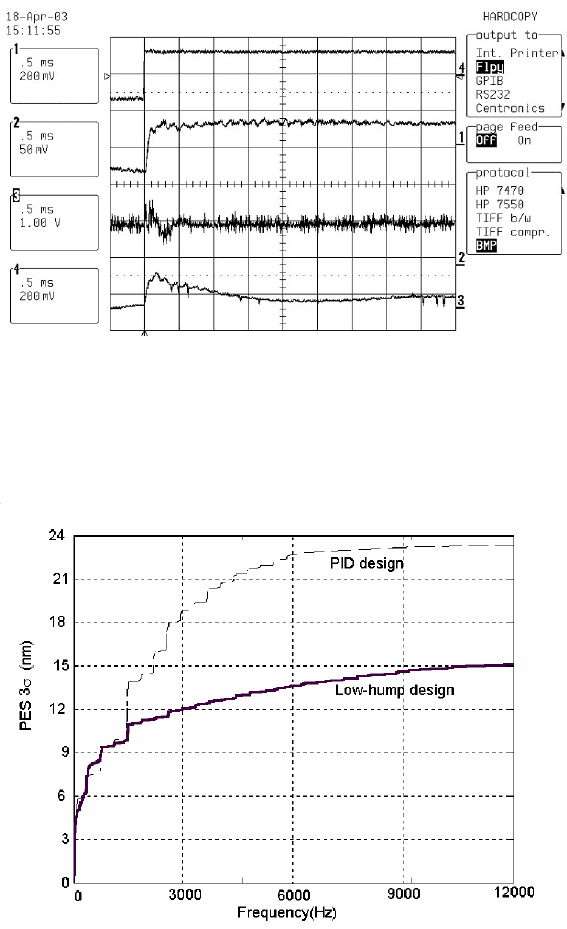
Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 151

FIGURE 7.20

Step response of t he dual-stage system.

FIGURE 7.21

3σ of PES NRRO versus frequencies.

152 Modeling and Control of Vibratio n in Mechanical Systems

7.4 Design in discrete- time domain

This part is concerned with servo loop con trol design in the discrete-time domain

that aims to achieve a low-hump sensitivity function for dual-stage actuator systems.

Before the cont rol design, sensitivity functions for a discrete-time d ual-stage system

will be analyzed on th e basis of the Bo de integral theorem.

7.4.1 Synthesis method for low-hump sensitiv ity function

We recall a simpliﬁed Bode’s theorem which is helpful to analyze the sensitivity

function of the dual-stage servo system.

THEOREM 7.1

Discrete Bode’s Theorem [104] Consider a discrete-time SISO LTI system

whose open-loop transfer function G (z) does not have unstable poles. The

sensitivity function of the system is given by S(z) = 1/(1 + G(z)). If the

closed-loop system is stable and k

= lim

z→∞

G(z), then

−π

ln |S(e

jω

)|dω = 2π(−ln|k

+ 1|). (7.1 7)

Based on the discrete Bode’s theorem, we have the following statements.

a). When G(z) is strictly proper, then lim

z→∞

G(z) = 0 and

−π

ln |S(e

jω

)|dω = 0.

b). When t he orders of the denominator and numerator o f G(z) are the same and

< −2 or k

> 0, then

−π

ln |S(e

jω

)|dω < 0.

c). When the ord ers of the denominator and numerator of G(z) are the same,

−2 ≤ k

< 0 and k

6= −1, then

−π

ln |S(e

jω

)|dω ≥ 0.

Thus, we can conclude that only if G(z) is non-strictly pr oper and k

< −2 or

> 0 , then

|S(e

jω

)| ≤ 1, ω ∈ [ 0, π],

i.e., the sensitivity function is bounded by 0 dB.

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 153

The open-loop transfer function of th e dual-stage parallel system is th e sum of

each path, i.e.,

G(z) = G

(z) + G

(z), (7.18)

(z) = P

(z)C

(z), (7.19 )

(z) = P

(z)C

(z). (7.20)

Note that a VCM actuator can be approximately represented by a double integrator

(i.e., k/s

) combined with some resonance modes and is often described by a strictl y

proper model. When G

(z) is str ictly proper, G(z) is also strictly proper and when

(z) is non- strictly proper, G(z) is non-strictly proper. I t can be concluded that

the Bode’s integral of the overall dual-stage loop is determined by the microactuator

loop. Only a non-strictly proper model of microactuator could possibl y produce a

“ﬂat” sensitivity function for dual-st age servo systems. An additional condition for

the “ﬂat” sensitivity is k

< −2 or k

> 0. These are necessary conditions and could

be used as a criterion to examine the closed-loop design.

In what follows, the di screte H

∞

loop shaping method will be applied to th e con-

trol designs of the VCM loop and t he microactuator loop such that the sensitivity

functions of the two loops are coupled and achieve a low-hump overall sensitivity.

The structure of the H

∞

loop shaping method is the same as in Figure 7.4. In the

discrete time case, Figure 7.4 is f ormulated as follows.

x(k + 1) = Ax(k) + B

w(k) + B

u(k), (7.21)

z(k) = C

x(k) + D

w(k) + D

u(k), (7.22 )

y(k) = C

x(k) + D

w(k) + D

u(k), (7.23 )

where

A =





, B





, B









, D

= D

, D

= D





, D

= 1, D

= D

, B

, C

, D

) and (A

, B

, C

, D

) are respectively the state-space real-

izations of plant P (z) and weighting function W (z). Let (A

, B

, C

, D

) be a

state space description of C(z). An LMI approach stated in Chapter 5 will be used

to d esign the controller C(z) : (A

, B

, C

, D

7.4.2 An application example

The VCM actuator and the microactuator are the same as those in Case 2 in Section

7.3.2. Notice that the PZT microactuator is represented using a Pade-delay with two

2nd order resonance terms. The form (7.14) can be regarded as a general model of

PZT actuated suspensions. It is strictly proper and th us according to the analysis in