Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems
Подождите немного. Документ загружается.

6
Mixed H
2
/H
∞
Control Design for Vibration
Rejection
6.1 Introduction
The mixed H
2
/H
∞
control problem i s concerned with the design of a controller that
minimizes the H
2
norm of a certain closed-loop transfer function while satisfying a
H
∞
norm constraint on the same or another closed-loop transfer function. One of the
important applications of this problem is to address t he optimal nominal p erformance
subject to a r obust stabil ity constraint.
In this chapter, we emplo y two methods: the one described in Chapter 5 and an
improved method. The two method s are applied to the control design in disk drives.
In order to meet the robustness requirement against unmodeled high frequency dy-
namics of the VCM actuator in disk drives, an H
∞
constraint is to be satisfied when
minimizi ng the H
2
performance of th e nominal sy stem. Hence, a mixed H
2
/H
∞
control can be formulat ed for disk drive control. Both the simulation and experiment
results d emonstrate that the mixed H
2
/H
∞
control design gives a significant perfor-
mance improvement of TMR over the conventional method of PID cont rol combined
with notch filters.
6.2 Mix ed H
2
/H
∞
control problem
This section aims t o derive an impr oved design method for the mixed H
2
/H
∞
control
which will give rise to an equal or better performance than the method in Chapter 5.
We consider the state-space representatio n for linear time-invariant systems:
x(k + 1) = Ax(k) + B
1
w(k) + B
2
u(k), (6.1)
y(k) = C
2
x(k) + D
21
w(k), (6.2)
z
1
(k) = C
z1
x(k) + D
z11
w(k) + D
z12
u(k), (6.3)
z
2
(k) = C
z2
x(k) + D
z21
w(k) + D
z22
u(k), (6.4)
where x(k) ∈ R
n
x
is the state, y(k) ∈ R
n
y
is the measurement outpu t, z
i
(k) ∈
115

116 Modeling and Control of Vibratio n in Mechanical Systems
R
n
z
(i = 1, 2) are the controlled outputs, w(k) ∈ R
n
w
is the disturbance input,
u(k) ∈ R
n
u
is the control input, and A, B
1
, B
2
, C
2
, D
21
, C
z1
, C
z2
, D
z11
, D
z12
,
D
z21
, D
z22
are of appropri at e dimensions.
Let a controller of the same dimension as that of the sy stem (6.1)−(6 .4) be of the
form:
x
c
(k + 1) = A
c
x
c
(k) + B
c
y(k), (6.5)
u(k) = C
c
x
c
(k) + D
c
y(k), (6.6)
where the matrices (A
c
, B
c
, C
c
, D
c
) are to be determined.
First, denote ξ = [x
T
x
T
c
]
T
. It follows f rom (6.1)−(6.4) and (6.5)−(6.6) that
ξ(k + 1) =
¯
Aξ(k) +
¯
Bw(k), (6.7)
z
1
(k) =
¯
C
1
ξ(k) +
¯
D
1
w(k), (6.8)
z
2
(k) =
¯
C
2
ξ(k) +
¯
D
2
w(k), (6.9)
where
¯
A =
A + B
2
D
c
C
2
B
2
C
c
B
c
C
2
A
c
,
¯
B =
B
2
D
c
D
21
+ B
1
B
c
D
21
, (6.10)
¯
C
1
= [C
z1
+ D
z12
D
c
C
2
D
z12
C
c
] ,
¯
D
1
= D
z12
D
c
D
21
+ D
z11
, (6.11)
¯
C
2
= [C
z2
+ D
z22
D
c
C
2
H
22
C
c
] ,
¯
D
2
= D
z22
D
c
D
21
+ D
z21
. (6.12)
Denote T
z
1
w
the transfer function matrix from w to z
1
, and T
z
2
w
the transfer
function matrix from w to z
2
. The mixed H
2
/H
∞
control problem is then stated as:
Given a positive scalar γ, design a control ler of the form (6.5)−(6.6) such that the
H
2
norm, kT
z
1
w
k
2
is minimized subject to the constraint kT
z
2
w
k
∞
< γ.
6.3 Method 1: slack variable approach
Given the solutions of H
2
control and H
∞
control in Chapter 5, the following solu-
tion to the mixed H
2
/H
∞
control follows directly.
THEOREM 6.1
Consider the system (6.1)−(6.4). Given scalars µ > 0 and γ > 0, a controller
of the form (6.5)−(6.6) that solves the mixed H
2
/H
∞
control problem exists
if the following conditions are satisfied.
T race(Π) < µ, (6.13 )
Π C
z1
X + D
z12
E C
z1
+ D
z12
D
c
C
2
∗ X + X
T
− P
2
I + Z
T
− J
∗ ∗ Y + Y
T
− H
> 0, (6.14)

Mixed H
2
/H
∞
Control Design for Vibration Rejection 117
P
2
J AX + B
2
E A + B
2
D
c
C
2
B
1
+ B
2
D
c
D
21
∗ H U Y A + W C
2
Y B
1
+ W D
21
∗ ∗ X + X
T
− P
2
I + Z
T
− J 0
∗ ∗ ∗ Y + Y
T
−H 0
∗ ∗ ∗ ∗ I
> 0, (6.15)
D
z11
+ D
z12
D
c
D
21
= 0, (6.16 )
and
P
∞
˜
J AX + B
2
E A + B
2
D
c
C
2
B
1
+ B
2
D
c
D
21
0
∗
˜
H U Y A + W C
2
Y B
1
+ W D
21
0
∗ ∗ X + X
T
−P
∞
I + Z
T
−
˜
J 0 X
T
C
T
z2
+ E
T
D
T
z22
∗ ∗ ∗ Y + Y
T
−
˜
H 0 C
T
z2
+ C
T
2
D
T
c
D
T
z22
∗ ∗ ∗ ∗ I D
T
z21
+ D
T
21
D
T
c
D
T
z22
∗ ∗ ∗ ∗ ∗ γI
> 0 , (6.17)
where the matrices X, E, Y , W , U, D
c
, Z, J,
˜
J and the symmetric matrices
P
2
, P
∞
, H,
˜
H and Π are the variables. A feasible mixed H
2
/H
∞
controller
is obtained by choosing N
1
and M
1
nonsingular such that N
1
M
1
= Z −Y X
and calculating
C
c
= (E − D
c
C
2
X)M
−1
1
, D
c
= D
c
, (6.18)
B
c
= N
−1
1
(W − Y B
2
D
c
), (6.19 )
A
c
= N
−1
1
(U − Y (A + B
2
D
c
C
2
)X − N
1
B
c
C
2
X − Y B
2
C
c
M
1
]M
−1
1
. (6.20)
In the early development of the mixed H
2
/H
∞
control, to solve the problem in
terms of LMIs, a sin gle Lyapunov matrix i s adopted for both the H
2
and H
∞
perfor-
mances, which is very conservative in general. A sig nificant improvement was made
in [90] where a slack variable techniq ue is introdu ced which separates the Lyapunov
matrices from the controller parameters and hence allows them to be different for
the H
2
and H
∞
performances. This is observed in the above theorem where the
Lyapunov matrices P
2
, J and H are used for H
2
performance and different matrices
P
∞
,
˜
J and
˜
H are u sed for H
∞
performance.
6.4 Method 2: an improved slack variabl e approach
Recall from Chapter 5 that for a given controller that stabilizes the system (6.7)−(6.9),
the H
2
norm square, kT
z
1
w
k
2
2
, can be computed by th e following minimization [95]:
min
(Q=Q
T
,Π=Π
T
)
T race(Π), (6.21)

118 Modeling and Control of Vibratio n in Mechanical Systems
subject to
¯
A
T
Q
¯
A −Q +
¯
C
T
1
¯
C
1
< 0 , (6.22)
¯
B
T
Q
¯
B +
¯
D
T
1
¯
D
1
< Π. (6.23)
The fo llowing lemma leads to an alternative approach for computing the H
2
norm
of the system (6.7)−(6.8).
LEMMA 6.1
The minimization of the H
2
norm square in (6.21) i s equivalent to the fol-
lowing minimization:
min
(Q=Q
T
,Π=Π
T
,Σ)
T race(Π), (6.24)
subject to
˜
A
T
diag{Q, I}
˜
A −
Q Σ
Σ
T
Π
< 0 , (6.25)
where
˜
A =
¯
A
¯
B
¯
C
1
¯
D
1
.
Proof First of all, (6.25) can be rewritten as
¯
A
T
Q
¯
A −Q +
¯
C
T
1
¯
C
1
¯
A
T
Q
¯
B +
¯
C
T
1
¯
D
1
−Σ
¯
B
T
Q
¯
A +
¯
D
T
1
¯
C
1
− Σ
T
¯
B
T
Q
¯
B +
¯
D
T
1
¯
D
1
−Π
< 0. (6.26)
It is then cl ear that if there exists a solution (Q, Π, Σ) to (6.25), the same Q and Π
also satisfy (6.22) and (6.23), respectively. On the other hand, if there exist Q and
Π satisfying (6.22) and (6.23), then (6.25) is also met by the same Q and Π and
Σ =
¯
A
T
Q
¯
B +
¯
C
T
1
¯
D
1
.
REMARK 6.1 The characterization of the H
2
norm in the above l emma
has the advantage that it provides a unified treatment of H
2
and H
∞
designs
via an LMI approach, as seen later. Furthermore, the additional pa rameter
Σ in (6.25) wil l offer an additional freedom in o ptimization of performance
when a mixed H
2
and H
∞
control design i s concerned.
Without loss of generality, we shall assume n
w
= n
z
, i.e. the disturbance in put
and the signal to b e controlled have the same dimension. Note t hat, if this is not the
case, some simple modification can render the requirement satisfied. For exampl e,
if n
w
< n
z
, th e matrices B
1
, D
21
, D
z11
and D
z21
can be augmented as
ˆ
B
1
=
[B
1
0
n
x
×(n
z
−n
w
)
],
ˆ
D
21
= [D
21
0
n
x
×(n
z
−n
w
)
],
ˆ
D
z11
= [D
z11
0
n
z
×(n
z
−n
w
)
] and
ˆ
D
z21
= [D
z21
0
n
z
×(n
z
−n
w
)
].

Mixed H
2
/H
∞
Control Design for Vibration Rejection 119
LEMMA 6.2
There exists a solution (Σ, Q, Π) with Q = Q
T
to (6.25) if and only if there
exist matrices (Σ, Π, Q, F, G) with Q = Q
T
and Π = Π
T
such that
−
Q Σ
Σ
T
Π
+
˜
A
T
F + F
T
˜
A −F
T
+
˜
A
T
G
−F + G
T
˜
A diag{Q, I} −(G + G
T
)
< 0.
(6.27 )
Proof First, if (6.25) holds for so me Q > 0, by applying the Schur complement,
it is easy to know that (6.27) is satisfied with F = 0 and G
T
= G = diag{Q, I}.
On the other hand, if (6.27) holds for some (Σ, Q, F, G), multiplying (6.27) from the
left and from the right by Γ
T
and Γ, respectively, where
Γ =
I
˜
A
,
(6.25) follows.
REMARK 6.2 It should be pointed out that (6.21)−(6.23) and Lemma
6.2 give equi valent computations of the H
2
norm of the system. For systems
without uncertainty, it is well known that (6.21)−(6.23) can be applied to
derive the optimal H
2
controller [95]. Hence, there is no advantage of using
Lemma 6.2. However, as will be seen later, when additional performances such
as the H
∞
performance are to b e met in addition to the H
2
performance, the
latter will result in a less or equally conservative design due to the additional
variables F and G. We observe that when F = 0 and Σ = 0, Lemma 6.2
reduces to the result in Theorem 6.1.
While Lemma 6.2 can be applied to compute the H
2
norm of the system ( 6.7)−(6.8)
when a contr oller (6.5)−(6.6) is given, it may not b e directly applicable to the H
2
control design problem due to the presence of the products of F w ith
˜
A and G with
˜
A. To overcome this difficulty, we specialize the matrices F and G as follows.
F =
λ
1
Φ 0
0 λ
2
I
, G =
Φ 0
0 λ
3
I
, (6.28 )
where Φ ∈ R
2n×2n
and λ
i
, i = 1, 2, 3 are real scaling parameters. While t his
specialization of F and G generally introduces some conservatism, it contain s three
additional variables λ
i
, i = 1, 2, 3 as compared to the result of Theorem 6.1 which
help reduce the design conservatism in Theorem 6.1.
Substituting (6.28) into (6.27) leads to
−Q + λ
1
¯
A
T
Φ + λ
1
Φ
T
¯
A λ
2
¯
C
1
T
+ λ
1
Φ
T
¯
B − Σ
λ
2
¯
C
1
+ λ
1
¯
B
T
Φ − Σ
T
− Π + λ
2
¯
D
T
1
+
¯
D
1
−λ
1
Φ + Φ
T
¯
A Φ
T
¯
B
λ
3
¯
C
1
−λ
2
I + λ
3
¯
D
1

120 Modeling and Control of Vibratio n in Mechanical Systems
−λ
1
Φ
T
+
¯
A
T
Φ λ
3
¯
C
T
1
¯
B
T
Φ − λ
2
I + λ
3
¯
D
T
1
Q − (Φ + Φ
T
) 0
0 (1 − 2λ
3
)I
< 0. (6.29)
A similar characterization for the H
∞
performance can be derived. Indeed, recall
that when the system (6.7) and (6.9) is known, it is stable with its H
∞
norm less than
γ if and onl y if there exists a matrix P = P
T
> 0 such that
˜
A
T
diag{P
∞
, I}
˜
A −diag{P
∞
, γ
2
I} < 0, (6.30 )
where
˜
A =
¯
A
¯
B
¯
C
2
¯
D
2
.
Observe that (6.30) turns ou t to be a special case of (6.25) with Π = γ
2
I and Σ = 0.
Thus, following a similar procedure for deriving (6.29), it can be shown that the
system (6.7) and (6.9) has an H
∞
performance γ if and only if for some real scalars
ε
i
, i = 1, 2, 3, there exist matri ces P
∞
= P
T
∞
> 0 and Φ such that
−P
∞
+ ε
1
(
¯
A
T
Φ + Φ
T
¯
A) ε
2
¯
C
2
T
+ ε
1
Φ
T
¯
B
ε
2
¯
C
2
+ ε
1
¯
B
T
Φ −γ
2
I + ε
2
¯
D
T
2
+
¯
D
2
−ε
1
Φ + Φ
T
¯
A Φ
T
¯
B
ε
3
¯
C
2
−ε
2
I + ε
3
¯
D
2
−ε
1
Φ
T
+
¯
A
T
Φ ε
3
¯
C
T
2
¯
B
T
Φ −ε
2
I + ε
3
¯
D
T
2
P − (Φ + Φ
T
) 0
0 (1 − 2ε
3
)I
< 0. (6.31)
REMARK 6.3 When setting ε
1
= ε
2
= 0 (i.e. setting F = 0) and ε
3
= 1
and by some row-col umn exchanges, the above i nequality reduces to
P
∞
− Φ − Φ
T
Φ
T
¯
A Φ
T
¯
B 0
¯
A
T
Φ −P
∞
0
¯
C
T
2
¯
B
T
Φ 0 −γ
2
I
¯
D
T
2
0
¯
C
2
¯
D
2
−I
< 0
which is the result in Chapter 5. Therefore, ε
i
, i = 1 , 2, 3 are additional
variables which can b e exploi ted to allevi ate the conservatism in the mixed
H
2
/H
∞
design of T heorem 6.1.
Denote
Ω (Π, X, Y, E, U, W, Z, D
c
,
¯
Q
11
=
¯
Q
T
11
,
¯
Q
12
,
¯
Q
22
=
¯
Q
T
22
,
¯
Σ
1
,
¯
Σ
2
, λ
i
, i = 1, 2, 3) =
Mixed H
2
/H
∞
Control Design for Vibration Rejection 121
−
¯
Q
11
+ λ
1
(AY + Y
T
A
T
+ E
T
B
T
2
+ B
2
E)
−
¯
Q
T
12
+ λ
1
(A
T
+ C
T
2
D
c
T
B
T
2
) + λ
1
U
T
λ
2
(C
z1
Y + D
z21
E) + λ
1
(B
T
1
+ D
T
21
D
c
T
B
T
2
) −
¯
Σ
T
1
−λ
1
Y
T
+ AY + B
2
E
−λ
1
I + U
λ
3
(C
z1
Y + D
z21
E)
∗
−
¯
Q
22
+ λ
1
(A
T
X + X
T
A) + λ
1
(C
T
2
W
T
+ W C
2
)
λ
2
(C
z1
+ D
z21
D
c
C
2
) + λ
1
B
T
X + λ
1
D
T
21
W
T
−
¯
Σ
T
2
−λ
1
Z + A + B
2
D
c
C
2
−λ
1
X + X
T
A + W C
2
λ
3
(C
z1
+ D
z21
D
c
C
2
)
∗ ∗
∗ ∗
−Π + λ
2
(D
T
21
D
c
T
D
T
z21
+ D
z21
D
c
D
21
+ D
T
z11
+ D
z11
) ∗
B
1
+ B
2
D
c
D
21
¯
Q
11
− (Y + Y
T
)
X
T
B
1
+ W D
21
¯
Q
T
12
− (I + Z
T
)
−λ
2
I + λ
3
(D
z11
+ D
z21
D
c
D
21
) 0
∗ ∗
∗ ∗
∗ ∗
∗ ∗
¯
Q
22
− (X + X
T
) ∗
0 (1 −2λ
3
)I
. (6.32 )
We have the following solution to the mixed H
2
/H
∞
control.
THEOREM 6.2
Consider the system (6.1)−(6.4). A controller of the form (6.5)−(6.6) that
solves the mixed H
2
/H
∞
control problem exists if for some λ
i
, ε
i
, i = 1, 2, 3,
there exists a solution (
¯
P
11
,
¯
P
12
,
¯
P
22
,
¯
Q
11
,
¯
Q
12
,
¯
Q
22
,
¯
Σ
1
,
¯
Σ
2
, X, Y, Π, U, E, Z, W ,
Ψ, D
c
) with
¯
Q = [
¯
Q
lj
] =
¯
Q
T
> 0 and
¯
P = [
¯
P
lj
] =
¯
P
T
> 0 to the following
optimization:
min T race(Π)
subject to
Ω (Π, X, Y, E, U, W, Z, D
c
,
¯
Q
11
,
¯
Q
12
,
¯
Q
22
,
¯
Σ
1
,
¯
Σ
2
, λ
i
,
i = 1, 2, 3 ) < 0, (6.33)
Ω (γ
2
I, X, Y, E, U, W, Z, D
c
,
¯
P
11
,
¯
P
12
,
¯
P
22
,
¯
Σ
1
,
¯
Σ
2
, ε
i
,
i = 1, 2, 3)|
¯
Σ
1
=
¯
Σ
2
=0
< 0. (6.34)
122 Modeling and Control of Vibratio n in Mechanical Systems
In this situation, a mixed H
2
/H
∞
controller is given by
A
c
= M
−T
1
(U − X
T
(A + B
2
D
c
C
2
)Y − X
T
B
2
C
c
N
1
−M
T
1
B
c
C
2
Y )N
−1
1
, (6.35 )
B
c
= M
−T
1
(W − X
T
B
2
D
c
), (6.36 )
C
c
= (E − D
c
C
2
Y )N
−1
1
, D
c
= D
c
, (6. 37)
where M
1
, N
1
satisfy N
T
1
M
1
= Z − Y
T
X.
Proof First, observe from (6.29) that Φ is invertible since Φ + Φ
T
> Q > 0.
Denote
Φ =
X M
M
1
U
, Φ
−1
=
Y H
N
1
E
,
and
J =
Y I
n
N
1
0
, J
1
= diag{J, I, J, I}.
Furth er, denote
E = D
c
C
2
Y + C
c
N
1
, (6.38 )
U = X
T
(A + B
2
D
c
C
2
)Y +
X
T
B
2
C
c
N
1
+ M
T
1
B
c
C
2
Y + M
T
1
A
c
N
1
, (6.39 )
W = X
T
B
2
D
c
+ M
T
1
B
c
, (6.40)
Z = Y
T
X + N
T
1
M
1
. (6.41 )
Multiplying from the left and the right of (6 .29) by J
T
1
and J
1
respectively and
applying (6.10), we o btain (6.33) wh ere
¯
Q = [
¯
Q
lj
] = J
T
QJ and [
¯
Σ
T
1
¯
Σ
T
2
] = Σ
T
J.
By applying a similar procedure to (6.31), (6.34) can be obtained.
If there exists a solution for the LMIs (6.33) and (6.34), it is easy to see that
Y + Y
T
I + Z
I + Z
T
X + X
T
>
¯
Q > 0.
Multiplying the above from the l eft by [Y
−T
−I] and from t he rig ht by [Y
−T
−I]
T
,
we obtain that
(X − Y
−T
Z) + (X − Y
−T
Z)
T
> 0.
It is then clear that Z −Y
T
X is invertible. Hence, there exist invertible matrices M
1
and N
1
such that Z −Y
T
X = N
T
1
M
1
. Thus, it follows from (6.38)−(6.41) that the
controller parameters of (6.5)−(6.6) can be obtai ned as in (6.35)−(6 .37).
REMARK 6.4 It is worth noting that when setting λ
1
= λ
2
= ε
1
=
ε
2
= 0, λ
3
= ε
3
= 1 and
¯
Σ
1
=
¯
Σ
2
= 0, Theorem 6.2 reduces to Theorem
6.1. Hence, by exploring the freedoms offered by these parameters, a less or
equally conservative mixed H
2
/H
∞
design can be achieved. Certainly, the
Mixed H
2
/H
∞
Control Design for Vibration Rejection 123
controller from Theorem 6.1 is derived by a convex optim ization and can be
further refined by an iterative procedure. In the disk drive application to
be presented later, we demonstrate that Method 2 can g ive a much better
performance than Method 1 with Theorem 6.1 together with an iterative
refinement in the latter design.
REMARK 6.5 Observe that for given λ
i
, ε
i
, i = 1, 2, 3, (6.33) and (6.34)
are linear in (
¯
P
11
,
¯
P
12
,
¯
P
22
,
¯
Q
11
,
¯
Q
12
,
¯
Q
22
,
¯
Σ
1
,
¯
Σ
2
, X, Y, Π, U, E, Z, W, D
c
), and
hence can be solved by employing the LMI Tool [69]. The problem of searching
for the optimal scaling parameters λ
i
, ε
i
, i = 1, 2, 3 in general m ay be nu-
merically costly although the function fm insearch in MATLAB Optimization
Toolbox may be applied.
6.5 Application in servo loop design for hard disk dri ves
6.5.1 Problem formulatio n
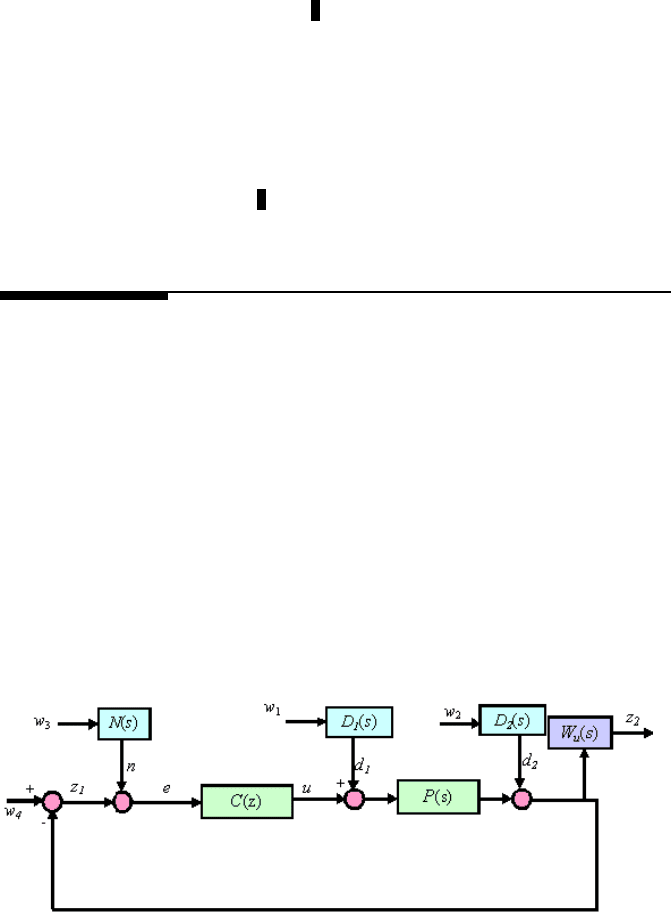
A block-diagram representation of a typical HDD servo loop is shown in Figure
6.1 with dist urbances injected. P (z) and C(z) represent transfer functions o f the
plant and controller, respectively. v represents all torque disturbances. d r epresents
disturbances that are due to non-repeatable disk and suspension/slider motions. n
denotes the PES demodulati on and measurement noise. z
1
is the true position error,
and e is the measured position error or measurement out put y in (6.2). D
1
, D
2
, and
N are the di sturbance and noise models, and w
1
, w
2
and w
3
are white noises of zero
mean and unit variance.
FIGURE 6.1
Mixed H
2
/H
∞
control scheme for HDD servo loop with disturbance models.
